安徽省六安市2023_2024学年高三数学上学期第二次月考试题含解析

这是一份安徽省六安市2023_2024学年高三数学上学期第二次月考试题含解析，共20页。试卷主要包含了 “是第一象限角”是“”的， 已知中，，，，则的面积是， 函数的图象最有可能是以下的， 设是函数的导函数，当时，，则， 已知函数的最小正周期为，则， 已知，，，下列选项正确的有等内容，欢迎下载使用。
时间：120分钟
一､单项选择题：本题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的.
1. “是第一象限角”是“”的（）
A. 充分不必要条件B. 必要不充分条件
C. 充要条件D. 既不充分也不必要条件
【答案】B
【解析】
【分析】根据充分、必要条件的定义，结合角的概念，即可得答案.
【详解】若是第一象限角，则，无法得到一定属于，充分性不成立，
若，则一定是第一象限角，必要性成立，
所以“是第一象限角”是“”的必要不充分条件.
故选：B
2. 已知中，，，，则的面积是（）
A. B. C. 6D.
【答案】A
【解析】
【分析】根据余弦定理求出，再求出，然后用面积公式即可.
【详解】，.
故选：A.
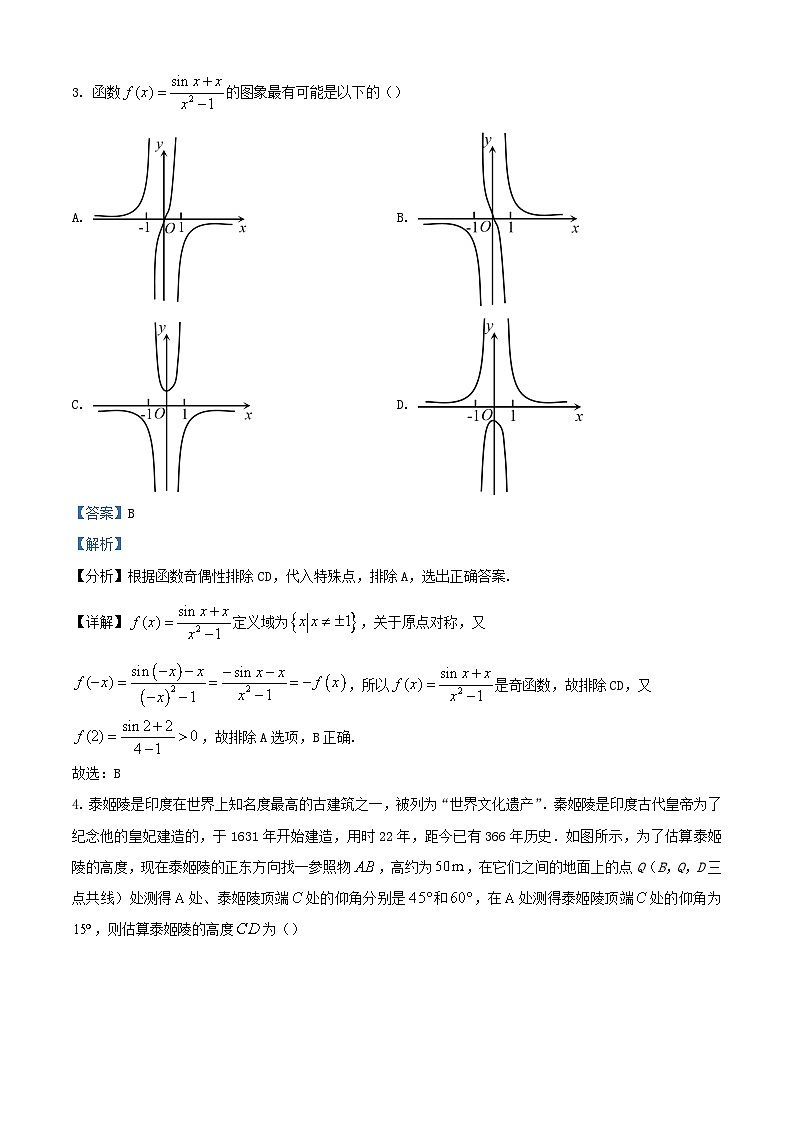
3. 函数的图象最有可能是以下的（）
A. B.
C. D.
【答案】B
【解析】
【分析】根据函数奇偶性排除CD，代入特殊点，排除A，选出正确答案.
【详解】定义域为，关于原点对称，又，所以是奇函数，故排除CD，又，故排除A选项，B正确.
故选：B
4. 泰姬陵是印度在世界上知名度最高的古建筑之一，被列为“世界文化遗产”．秦姬陵是印度古代皇帝为了纪念他的皇妃建造的，于1631年开始建造，用时22年，距今已有366年历史．如图所示，为了估算泰姬陵的高度，现在泰姬陵的正东方向找一参照物，高约为，在它们之间的地面上的点Q（B，Q，D三点共线）处测得处、泰姬陵顶端处的仰角分别是和，在处测得泰姬陵顶端处的仰角为，则估算泰姬陵的高度为（）
A. B. C. D.
【答案】A
【解析】
【分析】由题设可得，应用正弦定理求得，进而求.
【详解】由题设且，在测得泰姬陵顶端处仰角为，
所以，则，
所以，故.
故选：A
5. 声音是由于物体的振动产生的能引起听觉的波，我们听到的声音多为复合音.若一个复合音的数学模型是函数，则在区间上零点的个数是（）
A. 1B. 2C. 3D. 4
【答案】C
【解析】
【分析】由正弦的二倍角公式变形解方程可得.
【详解】，
或，又，∴，或，
故选：C．
6. 若是函数的一个极值点，则的极大值为（）
A. B. C. D.
【答案】D
【解析】
【分析】先对函数求导，由已知，先求出，再令，并判断函数在其左右两边的单调性，从而确定极大值点，然后带入原函数即可完成求解.
【详解】因为，，所以，
所以，，
令，解得或，
所以当，，单调递增；
时，，单调递减；
当，，单调递增，
所以的极大值为．
故选：D．
7. 已知函数在区间上是减函数，则实数的取值范围为（）
A. B. C. D.
【答案】B
【解析】
【分析】根据函数的单调性知导数小于等于0恒成立，分离参数后由正切函数单调性求解.
【详解】由题意，在上恒成立，
即在上恒成立，
因在上单调递增，所以，
所以在时，，
所以.
故选：B
8. 设是函数的导函数，当时，，则（）
A. B.
C. D.
【答案】B
【解析】
【分析】利用三角函数公式化简已知，再构造函数，利用函数单调性依次判断选项.
【详解】，
设在单调递增，
，所以A错误；
，
所以，所以B正确；
，所以C错误；
，
，所以D错误.
故选：B
二､多项选择题：本题共4小题，每小题5分，共20分.在每小题给出的选项中，有多项符合题目要求，全部选对的得5分，有选错的得0分，部分选对的得2分.
9. 已知函数的最小正周期为，则（）
A.
B. 直线是图象的一条对称轴
C. 在上单调递增
D. 将的图象上所有的点向右平移个单位长度，可得到的图象
【答案】AB
【解析】
【分析】根据辅助角公式和函数的最小正周期可得，然后利用的性质可得.
【详解】，
因最小正周期为，，故，得，
故，
选项A：
，故A正确；
选项B：
的对称轴为，，
即，，
当时，，故B正确；
选项C：
令，，
得，，
故的单调递减区间为，，
当时，的单调递减区间为，故C错误；
选项D：
将的图象上所有的点向右平移个单位长度，可得到，
故D错误
故选：AB
10. 已知，，，下列选项正确的有（）
A. B.
C. D.
【答案】BD
【解析】
【分析】根据同角关系以及诱导公式可得可得，进而可判断A，根据和差角公司以及二倍角公式即可代入求解BCD.
【详解】由于且，所以，
又，，
故或，当时，显然不满足，故，所以，故A错误，
对于B，，故B正确，
对于C, ，故C错误，
对于D，由B可知，所以，故D正确，
故选：BD
11. 已知函数，则下列结论正确的是（）
A. 的图象关于直线对称
B. 的图象关于点对称
C. 有3个零点
D. 是奇函数
【答案】BCD
【解析】
【分析】根据与的关系, 再由奇偶性的定义判来判断D，根据图象平移的关系即可判断BA，对于C，可以直接求出的零点，从而判断其正确与否.
【详解】的定义域为，的定义域为，
且，
记，则有，
故为奇函数，选项D正确；
由于为奇函数，图象关于原点对称，故的图象关于点对称，B正确，A错误
令，则有，即或，
解得或，即，或，
故有3个零点，选项C正确．
故选：BCD
12. 在△ABC中，已知a＝2b，且，则（）
A. a，c，b成等比数列
B.
C. 若a＝4，则
D. A，B，C成等差数列
【答案】ABC
【解析】
【分析】首先根据三角恒等变换，将已知条件化简得，再结合条件，再依次判断选项即可得到答案.
【详解】因为，
所以，
即，即.
对选项A，因为，所以、、成等比数列，故A正确；
对选项B，因为，，即，所以，
即，故B正确；
对选项C，若，则，，
则，
因为，所以.
故，故C正确.
对选项D，若、、成等差数列，则.
又因为，则.
因为，设，，，，
则，故D错误.
故选：ABC
三､填空题：本题共4小题，每小题5分，共20分.
13. “圆材埋壁”是我国古代的数学著作《九章算术》中的一个问题，现有一个“圆材埋壁”的模型，其截面如图所示，若圆柱形材料的底面半径为1，截面圆圆心为，墙壁截面为矩形，且，则扇形的面积是__________.
【答案】##
【解析】
【分析】计算，再利用扇形的面积公式求解.
【详解】由题意可知，圆的半径为，即，
又，所以为正三角形，∴，
所以扇形的面积是.
故答案为：
14. 已知是第三象限角，是终边上的一点，若，则______.
【答案】##0.5
【解析】
【分析】利用三角函数的定义求出的值，再利用二倍角公式求解即可.
【详解】因为是终边上的一点，所以,
则解得，
又因为是第三象限角，所以即，从而.
所以.
从而.
故答案为：
15. 已知函数在区间内恰有4个零点，则的取值范围是__________.
【答案】
【解析】
【分析】先求出的范围，结合的图像即可
【详解】因为，所以，
若在内恰有4个零点，则，解得.
故答案为：
16. 已知是定义在R上的偶函数，当时，，则不等式的解集是________．
【答案】
【解析】
【分析】利用导数判断当时，的单调性，结合偶函数解不等式.
【详解】当时，，，
则在上单调递增，
因为是定义在R上的偶函数，则在上单调递减，
若，即，
可得，解得，
所以不等式的解集是.
故答案为：.
四､解答题：本题共6小题，共70分.解答应写出文字说明､证明过程或演算步骤.
17. （1）已知，且，求的值；
（2）化简.
【答案】（1）（2）
【解析】
【分析】（1）确定得到，再根据三角恒等变换计算得到答案.
（2）根据二倍角公式和同角三角函数关系结合正弦的和差公式化简即可.
【详解】（1）平方得，故，
，则，，
.
（2）原式
18. 已知函数的图像相邻对称轴之间的距离是，若将的图像向右平移个单位，所得函数为奇函数.
（1）若，求的取值范围；
（2）设函数的零点为，求.
【答案】（1）
（2）
【解析】
【分析】（1）易得，由平移变换得到，根据为奇函数，求得，从而，再由，令，利用二次函数的性质求解；
（2）由函数的零点为，得到，再由，利用二倍角公式求解.
【小问1详解】
解：因为函数的图像相邻对称轴之间的距离是，
所以，解得，
所以，
当将的图像向右平移个单位，得到函数，
因为为奇函数，
所以，即，
因为，所以，
则；
则，
因为，所以，则，
所以.
【小问2详解】
因为函数的零点为，
所以，则，
所以，
.
19. 已知在中，角所对的边分别是，且
（1）求的大小；
（2）若，求的取值范围.
【答案】（1）
（2）
【解析】
【分析】（1）根据三角恒等变换化简，再由正余弦定理即可得解；
（2）由正弦定理，可将化为三角函数，再由三角函数的值域求范围即可.
【小问1详解】
因为，
所以，
整理得，由正弦定理得，
由余弦定理得，
因为，所以，
【小问2详解】
因，
所以，又，所以；
所以
又因为，则，
所以（当且仅当时，等号成立），
可得，即的取值范围是.
20. 已知函数
（1）求函数在区间上的单调递减区间；
（2）将函数的图象上所有的点向右平移个单位，再将所得图象上每一个点的横坐标变为原来的倍（纵坐标不变），再向上平移个单位，得到函数的图象.当时，方程恰有三个不相等的实数根、、，求实数的取值范围和的值.
【答案】（1）
（2），
【解析】
【分析】（1）利用三角恒等变换化简函数的解析式为，由求出的取值范围，再利用正弦型函数的单调性可求出函数在区间上的单调递减区间；
（2）利用三角函数图象变换可得出，令，，则函数与函数在时的图象有三个交点，数形结合可得出实数的取值范围，再利用正弦型函数的对称性可求得的值.
【小问1详解】
解：
，
因，则，
又在上单调递增，在上单调递减，
由可得，
即函数在区间上的单调递减区间为.
【小问2详解】
解：将函数的图象上所有的点向右平移个单位，
可得到函数的图象，
再把所得图象上每一个点的横坐标变为原来的倍（纵坐标不变），可得到函数的图象，
再将所得图象向上平移个单位，可得到函数的图象，
当时，，令，
则，令，
令，可得，其中，
作出函数与函数在时的图象如下图所示：
由图可知，当时，函数与函数在时的图象有三个交点，
设，其中，
则点与点关于直线对称，点与点关于直线对称，
所以，，，则，
所以，，解得
21. 记的内角、、的对边分别为、、，已知.
（1）求；
（2）若点在边上，且，，求.
【答案】（1）
（2）
【解析】
【分析】（1）由余弦定理化简可得出，可求出的值，再结合角的取值范围可求得角的值；
（2）求出、的值，设，则，分别在和中，利用正弦定理结合等式的性质可得出、的等式，即可求得的值，即为所求.
【小问1详解】
解：因为，
由余弦定理可得，
化简可得，由余弦定理可得，
因为，所以，.
【小问2详解】
解：因，则为锐角，所以，，
因为，所以，，
所以，，
设，则，
在和中，由正弦定理得，，
因为，上面两个等式相除可得，
得，即，
所以，.
22. 已知函数，
（1）若，求的单调区间；
（2）若，，是方程的两个实数根，证明：．
【答案】（1）单调递增区间为，单调递减区间为，
（2）证明见解析
【解析】
【分析】（1）利用函数的单调性与导数正负的关系即可求解；
（2）根据已知条件构造，利用导数法研究函数的单调性和最值，进而得出，的范围，再构造函数，利用导数法研究函数的单调性，结合函数单调性的性质即可求解.
【小问1详解】
由题可知的定义域为，
.
令，则的两根分别为，．
当或时，；
当时，；
所以的单调递增区间为，单调递减区间为，．
【小问2详解】
原方程可化为，
设，则，．
令，得．∵上，，在上，，
∴在上单调递增，在上单调递减，
∴，且当，趋向于0时，趋向于，
当趋向于时，趋向于．
则在和上分别有一个零点，，
不妨设，∵，∴，
设，则，
．
当时，，
∴在上单调递增，而，
∴当时，，，即．
∵，
∴．
∵在上单调递减，
∴，即．