河北省2024八年级数学上学期期中学情评估卷试卷（附答案人教版）

这是一份河北省2024八年级数学上学期期中学情评估卷试卷（附答案人教版），共14页。试卷主要包含了选择题等内容，欢迎下载使用。

1．下列各图是选自历届世博会会徽中的图案，其中是轴对称图形的个数为( )

A．3 B．2 C．1 D．0
2．现有3 cm，4 cm，7 cm，9 cm长的四根木棒，任取其中三根组成一个三角形，那么可以组成的三角形有( )
A．1个 B．2个 C．3个 D．4个
3．若一个多边形的外角和是它的内角和的eq \f(1,3)，则这个多边形是( )
A．五边形 B．六边形 C．七边形 D．八边形
4．如图，已知△ABC≌△DEC，点A和点D，点B和点E是对应顶点，过点A作AF⊥CD于点F，若∠BCE＝60°，则∠CAF的度数为( )
A．35° B．30° C．60° D．65°
(第4题) (第5题)
5．如图，已知P是∠AOB内一点，分别作点P关于直线OA，OB的对称点P1，P2，连接OP1，OP2，则下列结论正确的是( )
A．OP1⊥OP2 B．OP1＝OP2
C．OP1⊥OP2且OP1＝OP2 D．OP1≠OP2
6．为测量一池塘两端A，B间的距离．甲、乙两位同学分别设计了两种不同的方案．
甲：如图①，先过点B作AB的垂线BF，再在射线BF上取C，D两点，使BC＝CD，接着过点D作BD的垂线DE，交AC的延长线于点E，则测出DE的长即为A，B间的距离；
乙：如图②，先确定直线AB，过点B作射线BE，在射线BE上找可直接到达点A的点D，连接DA，作DC＝DA，交直线AB于点C，则测出BC的长即为A，B间的距离．则下列判断正确的是( )
A．只有甲同学的方案可行 B．只有乙同学的方案可行
C．甲、乙同学的方案均可行 D．甲、乙同学的方案均不可行
(第6题) (第7题)
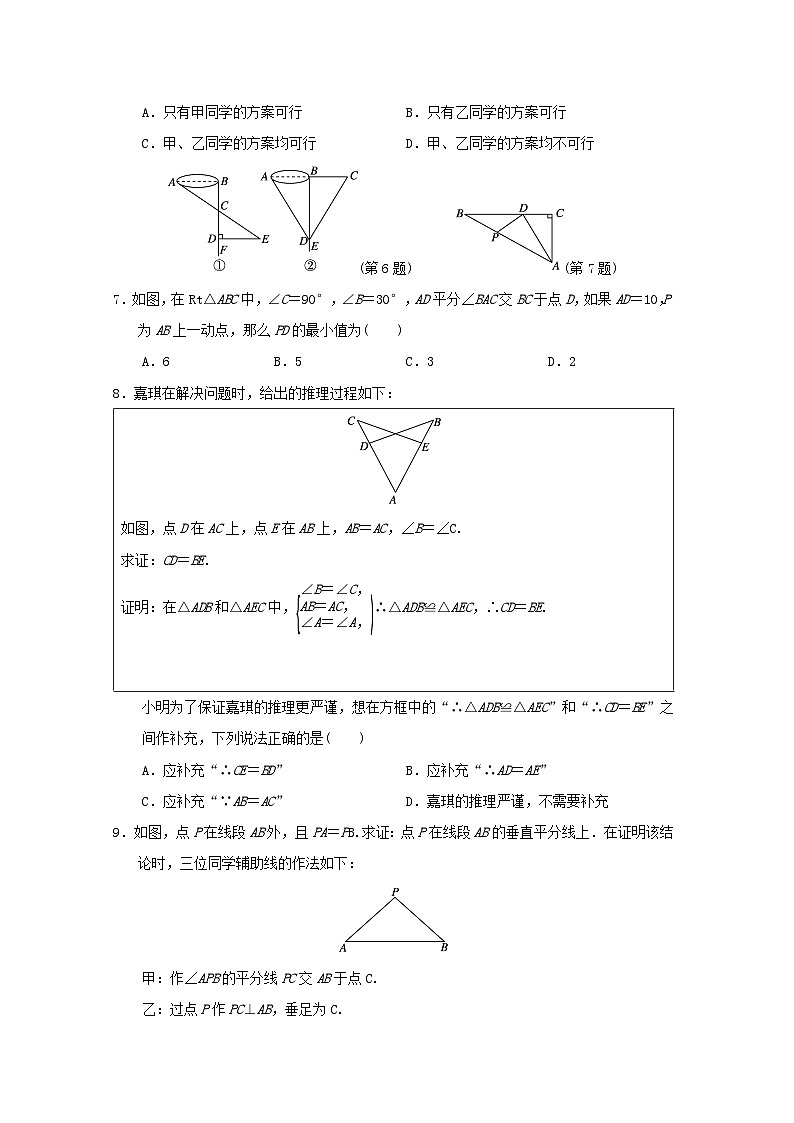
7．如图，在Rt△ABC中，∠C＝90°，∠B＝30°，AD平分∠BAC交BC于点D，如果AD＝10，P为AB上一动点，那么PD的最小值为( )
A．6 B．5 C．3 D．2
8．嘉琪在解决问题时，给出的推理过程如下：
小明为了保证嘉琪的推理更严谨，想在方框中的“∴△ADB≌△AEC”和“∴CD＝BE”之间作补充，下列说法正确的是( )
A．应补充“∴CE＝BD” B．应补充“∴AD＝AE”
C．应补充“∵AB＝AC” D．嘉琪的推理严谨，不需要补充
9．如图，点P在线段AB外，且PA＝PB.求证：点P在线段AB的垂直平分线上．在证明该结论时，三位同学辅助线的作法如下：
甲：作∠APB的平分线PC交AB于点C.
乙：过点P作PC⊥AB，垂足为C.
丙：过点P作PC⊥AB于点C，且AC＝BC.
其中，正确的是( )
A．甲和乙 B．甲和丙 C．乙和丙 D．全对
10．如图，在△ABC中，AB＝AC，边AC的垂直平分线MN分别交AB，AC于点M，N，点D是边BC的中点，点P是MN上任意一点，连接PD，PC，若∠A＝α，∠CPD＝β，当△PCD的周长取到最小值时，α，β之间的数量关系是( )
A．α＝β B．α＋β＝90°
C．α＋β＝180° D．以上都不正确
11．在△ABC中，∠ABC＝30°，边AB＝10，从4，5，7，9，11中取一值作为边AC的长．满足这些条件的互不全等的三角形的个数是( )
A．6 B．7 C．5 D．4
12．如图，∠EBF，∠EAC的平分线BP，AP交于点P，则下列结论中正确的有( )
①CP平分∠ACF；②∠ABC＋2∠APC＝180°；
③∠ACB＝2∠APB；④若PM⊥BE，PN⊥BF，则AM＋CN＝AC.
A．1个 B．2个 C．3个 D．4个
二、填空题(共4小题，每小题3分，共12分)13.如图，在△ABC中，点D，E分别为BC，AD的中点，且S△ABC＝4 cm2，则阴影部分的面积为________ cm2.
14．如图，在△PMN中，点P，M在坐标轴上，P(0，2)，N(2，－2)，PM＝PN，PM⊥PN，则点M的坐标是 ________．
15．综合与实践课上，同学们以“一个含30°角的直角三角板和两条平行线”为背景开展数学活动，如图，已知两直线a，b，且a∥b，在△ABC中，∠ACB＝90°，∠BAC＝30°.
(1)如图①，若∠1＝42°，则∠2＝____________°；
(2)小聪同学把图①中的直线a向上平移得到图②，则∠2－∠1＝________°；
(3)如图③，若∠2＝4∠1，则∠1＝________°.
(第15题) (第16题)
16．如图，在四边形ABCD中，AB＝10 cm，BC＝8 cm，CD＝12 cm，∠B＝∠C，点E为AB的中点．如果点P在线段BC上以3 cm/s的速度沿B－C－B运动，同时，点Q在线段CD上由点C向点D运动．当点Q的运动速度为________cm/s时，能够使△BPE与△CQP全等．
三、解答题(共8小题，共72分)17.(8分)如图，在平面直角坐标系中，A(4，－4)，B(1，－1)，C(3，－1)．
(1)画出△ABC关于x轴对称的△A1B1C1；
(2)直接写出点A1，B1，C1的坐标；
(3)在△A1B1C1中，∠A1≈27°，求B1C1边上的高与A1C1所夹角的度数．
18．(8分)常见的折叠椅如图所示．
(1)在点A，B，O处设置螺栓后可以使椅子变得牢固，其中的数学道理是________________；
(2)若AC，BD相交于点O，且O是AC，BD的中点．求证：AB＝CD.
19.(8分)小明将一副直角三角板按如图所示的方式摆放，其中△ABC是一个角(∠B)等于45°的直角三角板，△CDE是一个角(∠E)等于30°的直角三角板，小明摆放时确保点A在线段DE上，AB与CE相交于点F，且∠AFE＝105°.
(1)判断BC，ED的位置关系，并说明理由；
(2)直接写出图中等于75°的角．
20．(9分)阅读佳佳与明明的对话，解决下列问题．
(1)“多边形的内角和为2 020°”，为什么不可能？
(2)明明求的是几边形的内角和？
(3)错当成内角的那个外角为多少度？
21．(8分)如图，在△ABC中，AB＝CB，∠ABC＝90°，D为AB延长线上一点，点E在BC边上，且BE＝BD，连接AE，DC.
(1)求证：△ABE≌△CBD；
(2)若∠CAE＝24°，求∠BDC的度数．
22．(10分)如图，△ABC和△ACD都是边长为4厘米的等边三角形，两个动点P，Q同时从点A出发，点P以1厘米/秒的速度沿A→C→B的方向运动，点Q以2厘米/秒的速度沿A→B→C→D的方向运动，当点Q运动到点D时，P，Q两点同时停止运动．设P，Q运动的时间为t秒．
(1)点P，Q从出发到相遇所用时间是 ________秒；
(2)当t取何值时，△APQ也是等边三角形？请说明理由；
(3)当023.(10分)如图，在△ABC中，AD为BC边上的高，AE是∠BAD的平分线，F为AE上一点，连接BF，∠BFE＝45°.
(1)求证：BF平分∠ABE；
(2)连接CF交AD于点G，若S△ABF＝S△CBF，求证：∠AFC＝90°；
(3)在(2)的条件下，当BE＝3，AG＝4.5时，求线段AB的长．
24．(11分)【问题背景】
如图①，在四边形ABCD中，AB＝AD，∠BAD＝120°，∠B＝∠ADC＝90°，E，F分别是BC，CD上的点，且∠EAF＝60°，试探究线段BE，EF，FD之间的数量关系．
【初步探索】
小亮同学认为：延长FD到点G，使DG＝BE，连接AG，先证明△ABE≌△ADG，再证明△AEF≌△AGF，则可得到BE，EF，FD之间的数量关系是 ________________．
【探索延伸】
如图②，在四边形ABCD中，AB＝AD，∠B＋∠D＝180°，E，F分别是BC，CD上的点，∠EAF＝eq \f(1,2)∠BAD，上述结论是否仍然成立？说明理由．
【结论运用】
如图③，在某次军事演习中，舰艇甲在指挥中心(O处)北偏西30°的A处，舰艇乙在指挥中心南偏东70°的B处，并且两舰艇到指挥中心的距离相等，接到行动指令后，舰艇甲向正东方向以60海里/时的速度前进，舰艇乙沿北偏东50°的方向以80海里/时的速度前进，1.5小时后，指挥中心观测到甲、乙两舰艇分别到达E，F处，且两舰艇之间的夹角(∠EOF)为70°，试求此时两舰艇之间的距离．
答案
13.1 14.(－4，0) 15.(1)132 (2)120 (3)40
16.eq \f(9,13)或3或eq \f(5,4)或eq \f(15,4)
17．解：(1)如图，△A1B1C1即为所求．
(2)A1(4，4)，B1(1，1)，C1(3，1)．
(3)如图，作A1H⊥B1C1，垂足为H.
易知A1H＝B1H，∠A1HB1＝90°，
∴∠B1A1H＝45°，∴∠C1A1H≈45°－27°＝18°.
18．(1)三角形具有稳定性
(2)证明：∵O是AC，BD的中点，
∴OA＝OC，OB＝OD.
在△AOB和△COD中，eq \b\lc\{(\a\vs4\al\c1(OA＝OC，,∠AOB＝∠COD，,OB＝OD，))
∴△AOB≌△COD(SAS)，∴AB＝CD.
19．解：(1)BC，ED的位置关系是BC∥ED.
理由如下：∵∠AFE＝105°，∴∠AFC＝75°.
∵∠AFC是△FBC的一个外角，
∴∠AFC＝∠ECB＋∠B，
又∵∠B＝45°，∠E＝30°，
∴∠ECB＝75°－45°＝30°＝∠E，∴BC∥ED.
(2)题图中等于75°的角有三个，为∠AFC，∠EFB，∠ACD.
20．解：(1)设多边形的边数为n，
根据题意，得180°(n－2)＝2 020°，解得n＝13eq \f(2,9).
∵n为正整数，∴ “多边形的内角和为2 020°”不可能．
(2)设应加的内角为x，多加的外角为y，
依题意可列方程为180°(n－2)＝2 020°－y＋x，
∵－180°∴2 020°－180°<180°(n－2)<2 020°＋180°，
解得12eq \f(2,9)又∵n为正整数，∴n＝13，或n＝14.
∴明明求的是十三边形或十四边形的内角和．
(3)十三边形的内角和＝180°×(13－2)＝1 980°，
∴y－x＝2 020°－1 980°＝40°，
又∵x＋y＝180°，∴x＝70°，y＝110°.
十四边形的内角和＝180°×(14－2)＝2 160°，
∴y－x＝2 020°－2 160°＝－140°，
又∵x＋y＝180°，∴x＝160°，y＝20°.
∴错当成内角的那个外角为110°或20°.
21．(1)证明：∵∠ABC＝90°，
∴∠CBD＝180°－∠ABC＝90°，∴∠ABE＝∠CBD.
在△ABE和△CBD中，eq \b\lc\{(\a\vs4\al\c1(AB＝CB，,∠ABE＝∠CBD，,BE＝BD，))
∴△ABE≌△CBD(SAS)．
(2)解：∵AB＝CB，∠ABC＝90°，∴∠ACB＝45°，
由(1)得△ABE≌△CBD，∴∠AEB＝∠BDC.
∵∠AEB为△AEC的外角，
∴∠AEB＝∠ACB＋∠CAE＝45°＋24°＝69°，
∴∠BDC＝69°.
22．解：(1)4
(2)如图①，若△APQ是等边三角形，
此时点P在BC上，点Q在CD上，且易知△ADQ≌△ACP，
则CP＝DQ，即t－4＝4－(2t－8)，解得t＝eq \f(16,3).
(3)PQ与AC互相垂直．理由如下：
如图②，根据题意，得AQ＝2AP，取AQ的中点N，连接PN，则AP＝AN＝NQ.
∵∠PAQ＝60°，∴△APN是等边三角形，
∴∠APN＝∠ANP＝60°，PN＝AN＝NQ，
∴∠NPQ＝∠NQP＝30°，
∴∠APQ＝∠APN＋∠NPQ＝90°，
∴当023．(1)证明：∵AE是∠BAD的平分线，
∴∠BAD＝2∠BAF.
∵∠BFE＝45°，∴∠FBA＋∠BAF＝45°，
∴2∠FBA＋2∠BAF＝90°.
∵AD为BC边上的高，
∴∠EBF＋∠FBA＋2∠BAF＝90°，
∴2∠FBA＝∠EBF＋∠FBA，
∴∠EBF＝∠FBA，∴BF平分∠ABE.
(2)证明：如图，过点F作FM⊥BC于点M，FN⊥AB于点N.
∵BF平分∠ABE，FM⊥BC，FN⊥AB，∴FM＝FN.
∵S△ABF＝S△CBF，即eq \f(1,2)AB·FN＝eq \f(1,2)BC·FM，
∴AB＝BC.
在△ABF和△CBF中，
eq \b\lc\{(\a\vs4\al\c1(BA＝BC，,∠ABF＝∠CBF，,BF＝BF，))
∴△ABF≌△CBF(SAS)，
∴∠AFB＝∠CFB.
∵∠BFE＝45°，∴∠AFB＝135°，∴∠CFB＝135°，
∴∠CFE＝∠CFB－∠BFE＝135°－45°＝90°，
∴∠AFC＝90°.
(3)解：∵△ABF≌△CBF，∴AF＝FC.
∵∠AFC＝∠ADC＝90°，∠AGF＝∠CGD，
∴∠FAG＝∠FCE.
在△AFG和△CFE中，eq \b\lc\{(\a\vs4\al\c1(∠AFG＝∠CFE，,AF＝CF，,∠FAG＝∠FCE，))
∴△AFG≌△CFE(ASA)，∴EC＝AG＝4.5.
又∵BE＝3，∴BC＝BE＋EC＝7.5，
∴AB＝BC＝7.5.
24．解：初步探索：EF＝BE＋FD
探索延伸：结论仍然成立．理由：
如图①，延长FD到点G，使DG＝BE，连接AG.
∵∠B＋∠ADC＝180°，∠ADG＋∠ADC＝180°，
∴∠B＝∠ADG.
在△ABE和△ADG中，eq \b\lc\{(\a\vs4\al\c1(BE＝DG，,∠B＝∠ADG，,AB＝AD，))
∴△ABE≌△ADG，∴AE＝AG，∠BAE＝∠DAG.
∵∠EAF＝eq \f(1,2)∠BAD，
∴∠GAF＝∠DAG＋∠DAF＝∠BAE＋∠DAF＝∠BAD－∠EAF＝∠EAF.
在△AEF和△AGF中，eq \b\lc\{(\a\vs4\al\c1(AE＝AG，,∠EAF＝∠GAF，,AF＝AF，))
∴△AEF≌△AGF，∴EF＝FG.
∵FG＝DG＋FD＝BE＋FD，∴EF＝BE＋FD.
结论运用：如图②，连接EF，延长AE，BF交于点C.
∵∠AOB＝30°＋90°＋(90°－70°)＝140°，
∠EOF＝70°，
∴∠EOF＝eq \f(1,2)∠AOB.
∵OA＝OB，∠OAC＋∠OBC＝(90°－30°)＋(70°＋50°)＝180°，∴符合探索延伸中的条件，
∴结论EF＝AE＋BF成立，
∴EF＝1.5×(60＋80)＝210(海里)．
答：此时两舰艇之间的距离是210海里．
如图，点D在AC上，点E在AB上，AB＝AC，∠B＝∠C.
求证：CD＝BE.
证明：在△ADB和△AEC中，eq \b\lc\{(\a\vs4\al\c1(∠B＝∠C，,AB＝AC，,∠A＝∠A，))∴△ADB≌△AEC，∴CD＝BE.
答案
查速
1
2
3
4
5
6
7
8
9
10
11
12
B
B
D
B
B
A
B
B
A
A
A
D