江苏省宿迁市宿城区2024—2025学年上学期九年级期中考试数学试题(无答案)

这是一份江苏省宿迁市宿城区2024—2025学年上学期九年级期中考试数学试题(无答案)，共7页。试卷主要包含了选择题，解答题等内容，欢迎下载使用。

（总分：150分，时长：120分钟，日期：）
一、选择题（共8小题，每小题3分，满分24分．每个小题只有一个选项是正确的，请把正确选项的字母涂在答题卡相应的位置）
1．下列函数中一定是二次函数的是（ ）
A．B．C．D．
2．一组数据26，32，32，36，46，■7，52进行统计分析，其中一个两位数的十位上的数字被墨水涂污看不到，则下列统计量与被涂污数字无关的是（ ）
A．平均数B．中位数C．众数D．方差
3．如图，AB为⊙O的直径，C，D为⊙O上两点，，则的度数为（ ）
A．B．C．D．
4．某一芯片实现国产化后，经过两次降价，每块芯片单价由256元降为196元．若两次降价的百分率相同，设每次降价的百分率为x，根据题意列方程得（ ）
A．B．
C．D．
5．下列说法正确的是（ ）
A．两个半圆是等弧B．相等的圆心角所对的弧相等
C．三角形的外心到三角形的三边距离相等D．等弧所对的圆心角相等
6．如图，在一张纸片中，，O是它的内切圆．小明用剪刀沿着⊙O的切线DE剪下一块三角形ADE，则的周长为（ ）
A．5B．6C．7D．8
7．已知一组数据的平均数是4，方差是3，那么另一组数据的平均数和方差分别是（ ）
A．5，12B．5，3C．6，12D．6，3
8．如图，正方形ABCD中，，E是BC的中点．以点C为圆心，CE长为半径画圆，点P是⊙C上一动点，点F是边AD上一动点，连接AP，若点Q是AP的中点，连接BF，FQ，则的最小值为（ ）
A．B．C．6D．
二、填空题（本大题有10小题，每小题3分，共30分．
9．一组数据：，0，3，1，5，2的极差为________．
10．在一个不透明的口袋中放入只有颜色不同的白球6个，黑球4个，黄球n个，搅匀随机摸出一个球恰好是黄球的概率是．则________．
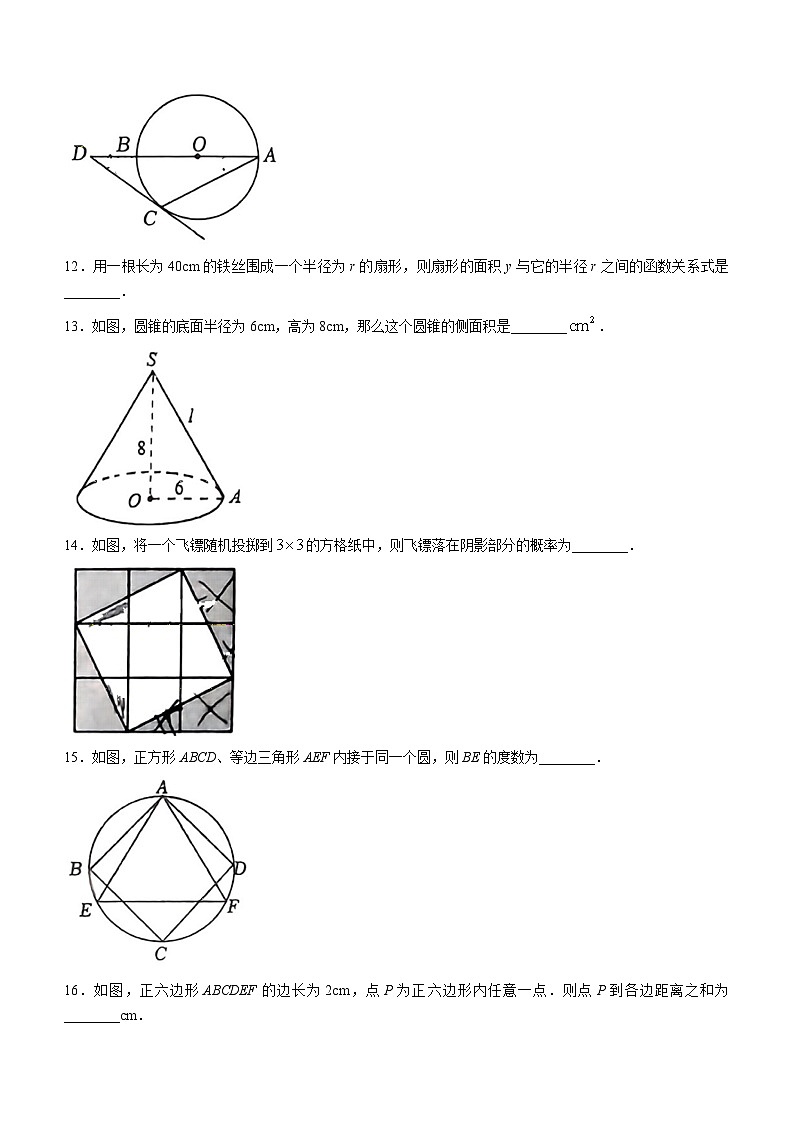
11．如图，AB是⊙O的直径，点D在AB的延长线上，DC切⊙O于点C，若，则的度数为________
12．用一根长为40cm的铁丝围成一个半径为r的扇形，则扇形的面积y与它的半径r之间的函数关系式是________．
13．如图，圆锥的底面半径为6cm，高为8cm，那么这个圆锥的侧面积是________．
14．如图，将一个飞镖随机投掷到的方格纸中，则飞镖落在阴影部分的概率为________．
15．如图，正方形ABCD、等边三角形AEF内接于同一个圆，则BE的度数为________．
16．如图，正六边形ABCDEF的边长为2cm，点P为正六边形内任意一点．则点P到各边距离之和为________cm．
17．设x，y是一个直角三角形两条直角边的长，且，则这个直角三角形的外接圆面积为________．
18．半圆O与平面直角坐标系交于点，点C在AB上运动（不与A，B重合），连接AC、BC，与的平分线交于点D，则C从A点运动到B点的过程中，点D的运动路径长为________．
三、解答题（本大题有10小题，共96分．解答时应写出文字说明或演算步骤．）
19．（本题8分）解方程：
（1）；（2）．
20．（本题8分）如图，在⊙O的内接四边形ABCD中，，点E在AD上．
（1）________°；
（2）求的度数．
21．（本题8分）已知关于x的一元二次方程．
（1）若方程有实数根，求实数m的取值范围；
（2）若方程两实数根为，且满足，求实数m的值．
22．（本题8分）中国古代有着辉煌的数学成就，《周髀算经》，《九章算术》，《海岛算经》，《孙子算经》等是我国古代数学的重要文献．
（1）小聪想从这4部数学名著中随机选择1部阅读，则他选中《九章算术》的概率为________；
（2）某中学拟从这4部数学名著中选择2部作为“数学文化”校本课程学习内容，请用列表法或树状图法求恰好选中《九章算术》和《孙子算经》的概率（《周髀算经》记为“A”，《九章算术》记为“B”，《海岛算经》记为“C”，《孙子算经》记为“D”）．
23．（本题10分）某校同学组织了一次经典朗读比赛，甲、乙两队各10人的比赛成绩如表（10分制）：
（1）甲队成绩的中位数是________分，乙队成绩的众数是________分；
（2）已知乙队的平均成绩是9分，请计算乙队的方差；
（3）已知甲队成绩的方差是1.4分，则成绩较为整齐的是________队．
24．（本题10分）如图，在中，，以AB为直径的⊙O分别交BC、AC于点D、G，过点D作于点E，交AB的延长线于点F．
（1）求证：EF与⊙O相切；
（2）当时，求阴影部分的面积．
25．（本题10分）在圆O中，点A，B，C均在⊙O上，请仅用无刻度直尺按要求画图：
图1 图2
（1）在图1中，以点C为顶点作一个锐角，使该锐角与互余；
（2）在图2中，弦且，过点A作一条直线将的面积平分．
26．（本题10分）“抖音”平台爆红网络，某电商在“抖音”上直播带货，已知该产品的进货价为70元/件，为吸引流量，该电商在直播中承诺自家商品价格永远不会超过99元/件，根据一个月的市场调研，商家发现当售价为110元/件时，日销售量为20件，售价每降低1元，日销售量增加2件；设商家降了x元．
（1）当产品售价为105元/件时，销售量为________件；
（2）该产品每件降价多少元时，电商每天可盈利1200元？
（3）该产品的售价每件应定为多少，电商每天可盈利最大并求出最大值？
27．（本题12分）我们在八年级上册曾经探索：把一个直立的火柴盒放倒（如图1），通过对梯形ABCD面积的不同方法计算，来验证勾股定理．a、b、c分别是和的边长，易知且，这时我们把关于x的形如的一元二次方程称为“勾氏方程”．
图1 图2
请解决下列问题：
（1）（填“是”或“不是”）“勾氏方程”；
（2）求证：关于x的“勾氏方程”必有实数根；
（3）如图2，⊙O的半径为5，AB、CD是位于圆心O异侧的两条平行弦，，关于x的方程是“勾氏方程”，连接AD，
①求的度数．
②直接写出BD的长：________．
28．（本题12分）
【了解概念】
我们知道，折线段是由两条不在同一直线上且有公共端点的线段组成的图形．如图1，线段MQ、QN组成折线段MQN．若点P在折线段MQN上，，则称点P是折线段MQN的中点．
图1 图2
【理解应用】
（1）如图2，⊙O的半径为2，PA是⊙O的切线，A为切点，点B是折线段POA的中点．若，则________；
【定理证明】
（2）阿基米德折弦定理：如图3，AB和BC是⊙O的两条弦（即折线段ABC是圆的一条折弦），，点M是ABC的中点，从M向BC作垂线，垂足为D，求证：D是折弦ABC的中点；
【变式探究】
（3）如图4，若点M是AC的中点，【定理证明】中的其他条件不变，则CD、DB、BA之间存在怎样的数量关系？请直接写出结论．
【灵活应用】
（4）如图5，BC是⊙O的直径，点A为⊙O上一定点，点D为⊙O上一动点，且满足，若则________．
图3 图4 图5甲
7
8
9
7
10
10
9
10
10
10
乙
10
8
7
9
8
10
10
9
10
9