

人教B版 (2019)选择性必修 第一册1.2.3 直线与平面的夹角一课一练
展开知识点01 直线与平面的夹角
1.直线与平面垂直:直线与平面的夹角为90°.
2.直线与平面平行或在平面内:直线与平面的夹角为0°.
3.斜线和平面所成的角:斜线和它在平面内的射影所成的角,叫做斜线和平面所成的角(或斜线和平面的夹角)
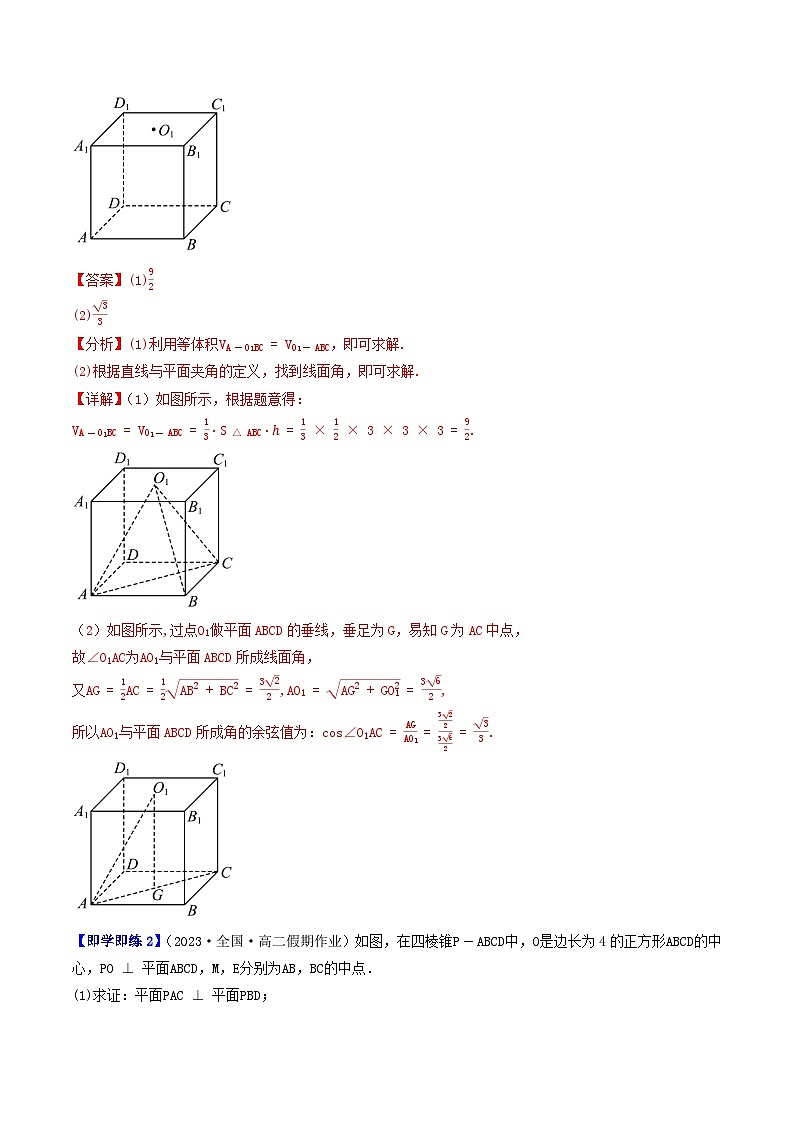
【即学即练1】(浙江省绍兴市2022-2023学年)在正方体ABCD-A1B1C1D1中,棱长为3,O1是上底面A1B1C1D1的一个动点.
(1)求三棱锥A-O1BC的体积;
(2)当O1是上底面A1B1C1D1的中心时,求AO1与平面ABCD所成角的余弦值.
【答案】(1)92
(2)33
【分析】(1)利用等体积VA-O1BC=VO1-ABC,即可求解.
(2)根据直线与平面夹角的定义,找到线面角,即可求解.
【详解】(1)如图所示,根据题意得:
VA-O1BC=VO1-ABC=13⋅S△ABC⋅h=13×12×3×3×3=92.
(2)如图所示,过点O1做平面ABCD的垂线,垂足为G,易知G为AC中点,
故∠O1AC为AO1与平面ABCD所成线面角,
又AG=12AC=12AB2+BC2=322,AO1=AG2+GO12=362,
所以AO1与平面ABCD所成角的余弦值为:cs∠O1AC=AGAO1=322362=33.
【即学即练2】(2023·全国·高二假期作业)如图,在四棱锥P-ABCD中,O是边长为4的正方形ABCD的中心,PO⊥平面ABCD,M,E分别为AB,BC的中点.
(1)求证:平面PAC⊥平面PBD;
(2)若PE=3,求点B到平面PEM的距离;
(3)若PE=3,求直线PB与平面PEM所成角的余弦值.
【答案】(1)证明见解析
(2)707
(3)99191.
【分析】(1)先证明AC⊥平面PBD,再根据面面垂直的判定定理证明平面PAC⊥平面PBD;
(2)利用几何关系和等体积法求解即可.
(3)由(2)可知点B到平面PEM的距离为h=707,计算PB的长度,根据直线与平面所成的角的定义求解.
【详解】(1)因为四边形ABCD是正方形,所以AC⊥BD,
因为PO⊥平面ABCD,AC⊂平面ABCD,所以AC⊥PO,
因为OP⊂平面PBD,BD⊂平面PBD,且OP∩BD=O,
所以AC⊥平面PBD.又AC⊂平面PAC,所以平面PAC⊥平面PBD.
(2)由(1)知,PO为点P到平面BME的距离.
所以VB-PEM=VP-BEM=13S△BEM×OP,
连接OE.因为PO⊥平面ABCD,OE⊂平面ABCD,所以PO⊥OE,
因为OE=2,PE=3,所以PO=5,
又因为OA=OB=OC=OD=22,所以PA=PB=PC=PD.
在△PEM中,PE=PM=3,ME=12AC=22,
所以S△PEM=12×22×32-(2)2=14,
设点B到平面PEM的距离为h,
由VB-PEM=13×S△PEM×h=VP-BEM=13S△BEM×PO=13×12×2×2×5=253,
得143h=253,所以h=707.
所以点B到平面PEM的距离为707.
(3)若PE=3,由(2)可知,点B到平面PEM的距离为h=707,
又PB=PO2+OB2=5+8=13,
设直线PB与平面PEM所成角为θ,
所以sinθ=hPB=70713=70713,
所以csθ=1-sin2θ=1-(70713)2=99191.
即直线PB与平面PEM所成角的余弦值为99191.
知识点02 用空间向量求直线与平面的夹角
1.定义:设直线l的方向向量为u,平面α的法向量为n,直线与平面所成的角为θ,u与n 的角为φ,则有sinθ=__csφ ____=___u⋅nun____.
2.范围:[0,π2]
【即学即练3】若正三棱柱ABC-A1B1C1的所有棱长都相等,D是A1C1的中点,则直线AD与平面B1DC所成角的余弦值为______.
【答案】35##0.6
【分析】利用空间向量的坐标运算求解线面角即可.
【详解】
如图,取AC中点O,连接OB,OD,
则有OD⊥OB,OD⊥OC,OB⊥OC,
所以以OB,OC,OD为x,y,z轴正方向建系如图,设AB=2,
则A(0,-1,0),D(0,0,2),B1(3,0,2),C(0,1,0),
AD=(0,1,2),DB1=(3,0,0),DC=(0,1,-2),
设平面B1DC的法向量为m=(x,y,z),
则有DB1⋅m=3x=0DC⋅m=y-2z=0,令y=2,则z=1,x=0,
所以m=(0,2,1),
设直线AD与平面B1DC所成角为θ,
则sinθ=cs
因为θ∈0,π2,所以csθ=35
故答案为: 35.
【即学即练4】(2023秋·山西晋中·高二统考期末)如图所示,在棱长为2的正四面体A-BCD中,E为等边三角形ACD的中心,F,G分别满足BF=12FC,BG=GA.
(1)用BA,BC,BD表示BE,并求出BE;
(2)求直线FG与平面ACD所成角的正弦值.
【答案】(1)BE=13BA+BC+BD,263
(2)4221
【分析】(1)先利用正四面体几何性质用BA,BC,BD表示BE,进而求得BE;
(2)先求得直线FG与直线BE所成角的余弦值,进而得到直线FG与平面ACD所成角的正弦值.
【详解】(1)连接AE并延长交CD于M,则M为CD中点,
则AE=23AM=23×12AC+AD=13AC+AD,
BE=BA+AE=BA+13AC+AD =BA+13BC-BA+BD-BA=13BA+BC+BD,
则BE=13BA+BC+BD=13BA+BC+BD2
=13BA2+BC2+BD2+2BA⋅BC+2BA⋅BD+2BC⋅BD
=134+4+4+4+4+4=263
(2)根据题意,BE⊥平面ACD,因此,直线FG与平面ACD所成角的正弦值
即为直线FG与直线BE所成角的余弦值的绝对值.
FG=12BA-13BC,
且FG=12BA-13BC=12BA-13BC2
=14BA2+19BC2-13BA⋅BC=14×4+19×4-13×2=73
故csFG,BE=FG⋅BEFGBE.
=13BA+BC+BD⋅12BA-13BC263×73
=1312BA2+16BA⋅BC+12BA⋅BD-13BC2-13BC⋅BD263×73
=132+13+1-43-23263×73=49263×73=4221
则直线FG与平面ACD所成角的正弦值为4221.
难点:动点问题
示例1:(多选)(23-24高二下·江苏徐州·期末)如图,在边长为12的正方形ABCD中,E1,E2,F1,F2分别边AD,BC的三等分点,正方形内有两点P,Q,点P到AD,CD的距离分别为3a,2a,点Q到BC,AB的距离也是3a和2a,其中0
B.PQ的最小值为6105
C.线段PQ的中点到A的距离不超过35
D.异面直线PQ与AB成45°角时,a=32
【答案】ABD
【分析】根据条件,建立如图所示的空间直角坐标系,求得PQ=(0,-2a,6a-12),选项A,先求出平面E1E2F2F1的一个法向量n,利用PQ⋅n=0,即可求解;选项B,因为PQ=40a2-144a+144,利用二次函数的性质,即可求解;选项C,求出PQ的中点S及A的坐标,即可求解;选项D,利用线线角的向量法,即可求解.
【详解】如图,取E1E2中点O1,F1F2的中点O,连接OB,OO1,
因为BF2=F2F1=F1B=4,所以BO⊥F1F2,
因为E1F1⊥F1B,E1F1⊥F1F2,又F1B∩F1F2,F1B,F1F2⊂面BF1F2,
所以E1F1⊥面BF1F2,又OO1//E1F1,所以OO1⊥面BF1F2,
故OB, OF2,OO1两两垂直,建立如图所示的空间直角坐标系,
设QH⊥BF1于H,PM⊥BF2于M,过H作HK⊥OB于K,
易知OB=23,BH=2a,又∠HBO=π6,所以HK=a,BK=3a,又QH=3a,
所以Q(23-3a,-a,3a),同理可知P(23-3a,a,12-3a),所以PQ=(0,-2a,6a-12),
对于选项A,易知平面E1E2F2F1的一个法向量为n=(1,0,0),因为PQ⋅n=0,
显然QP⊄平面E1E2F2F1,所以PQ //平面E1E2F2F1,故选项A正确,
对于选项B,因为PQ=4a2+(6a-12)2=40a2-144a+144,
令y=40a2-144a+144,其中0
所以PQmin=725=6105,故选项B正确,
对于选项C,因为PQ的中点S(23-3a,0,6),A(23,0,12),
所以AS=3a2+36<48,48>45=35 ,故选项C错误,
对于选项D,因为B(23,0,0),所以BA=(0,0,12),
所以cs45°=(6a-12)×124a2+(6a-12)2×12,整理得到2a2-9a+9=0,
解得a=32或a=3(舍),故选项D正确,
故选:ABD.
【点睛】关键点点晴:本题的关键在于建立空间直角坐标系,求出PQ=(0,-2a,6a-12),再利用线面平行的向量法、空间两点间的距离及线线角的向量法,即可求解.
【题型1:定义法求直线与平面所成的角】
例1.(23-24高二下·安徽·阶段练习)在棱长均相等的正三棱柱ABC-A1B1C1中,E为棱AB的中点,则直线B1E与平面BB1C1C所成角的正弦值为( )
A.1510B.13C.23D.5117
【答案】A
【分析】本题线面角的定义,作出线面角,根据勾股定理算出线面角所在直角三角形的边长,进而求出正弦值.
【详解】过E作EF⊥BC,F为垂足,连接B1F,则∠EB1F为直线B1E与平面B1C所成角,
设三棱柱的棱长为2,则EF=32,B1E=5,
∴sin∠EB1F=1510.
故选:A
变式1.(23-24高二下·河南·阶段练习)在直三棱柱ABC-A1B1C1中,∠BAC=90∘,AB=AC,AA1=BC,则BC1与平面ABB1A1所成的角为( ).
A.π6B.π4C.π3D.5π6
【答案】A
【分析】由AB⊥AC,AA1⊥AC,得到AC⊥平面ABB1A1,从而有A1C1⊥平面ABB1A1,∠A1BC1即为所求线面角,在Rt△A1BC1中,由长度关系求得∠A1BC1.
【详解】由题意,AB⊥AC,AA1⊥AC,可知AC⊥平面ABB1A1,
则有A1C1⊥平面ABB1A1,∠A1BC1即为所求线面角,
不妨设AB=AC=a,则BB1=BC=2a,A1B=3a,
故tan∠A1BC1=A1C1A1B=33,故∠A1BC1=π6.
故选:A.
变式2.(2023·湖南岳阳·模拟预测)如图,在正方体ABCD-A1B1C1D1中,直线AA1与平面ABC1D1所成的角为( )
A.30∘B.45∘C.60∘D.90∘
【答案】B
【分析】连接A1D,证明A1D⊥平面ABC1D1,则∠D1AA1即为直线AA1与平面ABC1D1所成角的平面角,即可得解.
【详解】连接A1D,则AD1⊥A1D,
因为AB⊥平面AA1D1D,AD1⊂平面AA1D1D,
所以AB⊥A1D,
又AB∩AD1=A,AB,AD1⊂平面ABC1D1,
所以A1D⊥平面ABC1D1,
所以∠D1AA1即为直线AA1与平面ABC1D1所成角的平面角,
在等腰直角三角形AA1D1中,∠D1AA1=45∘,
所以直线AA1与平面ABC1D1所成的角为45∘.
故选:B.
变式3.(多选)(22-23高二上·贵州黔东南·开学考试)已知梯形ABCD,AB=AD=1,BC=2,AD//BC,AD⊥AB,P是线段BC的中点.将△ABD沿着BD所在的直线翻折成四面体ABCD,翻折的过程中下列选项正确的是( )
A.BD与AP始终垂直
B.当直线AP与平面BCD所成角为π6时,AP=62
C.四面体A-BCD体积的最大值为22
D.四面体ABCD的外接球的表面积的最小值为4π
【答案】ABD
【分析】利用线面垂直的判定定理可得BD⊥平面OAP,进而可判断A选项;由直线AP与平面BCD所成角为π6得∠APO=π6,取AP的中点E,由AP=2PE=2POcs∠APO可判断B选项;当OA⊥平面BCD时,四面体A-BCD体积最大,进而可判断C选项;由题意确定球心,进而求半径的最小值,可判断D选项.
【详解】对于A:连接DP,AP,DP∩AP=O,如图所示:
易知四边形ABPD是正方形,所以BD⊥AP,
于是在四面体ABCD中,
BD⊥OA,BD⊥OP,
又OA∩OP=O且OA,OP⊂平面OAP,
BD⊥平面OAP,
又因为AP⊂平面OAP,所以BD⊥AP,故A正确;
对于B:取AP的中点E,连接OE,
因为OA=OP=22,所以OE⊥AP.
当直线AP与平面BCD所成角为π6时,∠APO=π6,
所以AP=2PE=2POcs∠APO=2×32=62,故B正确;
对于C:由题意可知,当OA⊥平面BCD时,四面体A-BCD体积最大,
于是VA-BCD=13SBCD⋅OA=13×12BC⋅DP⋅22=26,故C错误;
对于D:因为AB⊥AD,所以△ABD外接圆的圆心为O,
又因为BD⊥CD,所以△BDC外接圆的圆心为P.
分别过点O,P作平面ABD和BDC的垂线,交于点O1,
则O1是四面体ABCD的外接球的球心.
R=O1B=BP2+O1P2≥BP=1,当O1与P重合时取等号,
所以四面体ABCD的外接球的表面积的最小值为4πR2=4π,故D正确.
故选:ABD.
【点睛】方法点睛:解决与球相关的切、接问题,其通法是作出截面,将空间几何问题转化为平面几何问题求解,其解题思维流程如下:
(1)定球心:如果是内切球,球心到切点的距离相等且为球的半径;如果是外接球,球心到接点的距离相等且为半径;
(2)作截面:选准最佳角度做出截面(要使这个截面尽可能多的包含球、几何体的各种元素以及体现这些元素的关系),达到空间问题平面化的目的;
(3)求半径下结论:根据作出截面中的几何元素,建立关于球的半径的方程,并求解.
变式4.(多选)(23-24高二下·四川泸州·期末)如图,在棱长为32的正方体ABCD-A1B1C1D1中,点P是平面A1BC1内一个动点,且满足PD+PB1=3+33,则下列结论正确的是( )
A.B1D⊥PB
B.直线B1P与平面A1BC1所成角为定值
C.点P的轨迹的周长为33π
D.三棱锥P-BB1C1体积的最大值为62
【答案】ABD
【分析】利用线面垂直的判定定理、性质定理可判断A;求出点P的轨迹可判断C;求出直线B1P与平面A1BC1所成角可判断B;求出三棱锥B1-BPC1体积的最大值可判断D.
【详解】对于A,连接B1D1,因为四边形A1B1C1D1为正方形,则A1C1⊥B1D1,
因为DD1⊥平面A1B1C1D1,A1C1⊂平面A1B1C1D1,则A1C1⊥DD1,
因为B1D1∩DD1=D1,B1D1、DD1⊂平面B1DD1,所以A1C1⊥平面B1DD1,
B1D⊂平面B1DD1,所以B1D⊥A1C1,同理可得B1D⊥A1B,
因为A1C1∩A1B=A1,A1C1、A1B⊂平面A1BC1,所以B1D⊥平面A1BC1,
因为PB⊂平面A1BC1,所以B1D⊥PB,故A正确;
对于C, 由A选项知B1D⊥平面A1BC1,设B1D∩平面A1BC1=E,
即B1E⊥平面A1BC1,DE⊥平面A1BC1,
因为A1B=BC1=A1C1=6,A1B1=BB1=B1C1=32,
所以三棱锥B1-A1BC1为正三棱锥,因为B1E⊥平面A1BC1,
则E与正△A1BC1的中心,则BE=A1B2sinπ3=23,
所以B1E=BB12-BE2=6,因为B1D=3322=36,
所以DE=26,因为PD+PB1=3+33,
即PE2+DE2+PE2+EB12=3+33,
即PE2+24+PE2+6=3+33,
PE2+6=3+33-PE2+24,两边平方化简可得PE=3 PE>0,
因为E点到等边三角形A1BC1的边的距离为13×32×6=3=PE,
所以点P的轨迹是在△A1BC1内,且以E为圆心、半径为3的圆,
所以点P的轨迹的周长为23π,故C错误;
对于B,由选项C可知,点P的轨迹是在△A1BC1内,
且以E为圆心、半径为3的圆,EP=3,且B1E=6,
B1E⊥平面A1BC1,所以∠B1PE就是直线B1P与平面A1BC1所成角,
所以tan∠B1PE=B1EPE=63=2,因为0<∠B1PE<π2,
所以直线B1P与平面A1BC1所成角为定值,故B正确;
对于D,因为点E到直线BC1的距离为3,
点P到直线BC1的最大距离为3+3=23,
故△BPC1的面积的最大值为12×23×6=63,
因为B1E⊥平面A1BC1,则
三棱锥B1-BPC1体积的最大值为13×63×6=62,故D正确.
故选:ABD.
【点睛】关键点点睛:选项C的解题关键点是求出点P的轨迹;选项B的解题的关键点求出直线B1P与平面A1BC1所成角.
变式5.(24-25高二上·上海·课后作业)如图,平面OAB⊥平面α,OA⊂α,OA=AB,∠OAB=120°.平面α内一点P满足PA⊥PB,记直线OP与平面OAB所成角为θ,求tanθ的最大值.
【答案】612
【分析】作出图形,找出直线OP与平面OAB所成的角θ,证出PA⊥平面PBH,得出PA⊥PH,得出点P的轨迹就是平面α内以线段AH为直径的圆(点A除外),转化成与圆有关的最值问题,即可求出结果.
【详解】如图①所示,过B作BH⊥OA的延长线,垂足为H,
连接PH、OP,取AH的中点E,连接PE,
过点P作PF⊥OA,垂足为F.
∵平面OAB⊥平面α,且平面OAB∩平面α=OA,BH⊂平面OAB,PF⊂α,
∴BH⊥α,PF⊥平面OAB,
∴OP在平面OAB上的射影就是直线OA,
故∠AOP就是直线OP与平面OAB所成角θ,
即∠AOP=θ.
∵PA⊂α,∴PA⊥BH,
又∵PA⊥PB,PB∩BH=B,
∴PA⊥平面PBH,则PA⊥PH.
∴点P的轨迹是平面α内以线段AH为直径的圆(A点除外).
∵OA=AB,且∠OAB=120°,
∴∠BAH=60°,设OA=aa>0,则AB=a,
从而AH=AB⋅cs60°=a2,
∴PE=12AH=a4,如图②所示,
当且仅当PE⊥OP,即OP是圆E的切线时,
角θ有最大值,tanθ有最大值,
tanθ的最大值为PEOP=PEOE2-PE2=a4a+a42-a42=612.
【点睛】关键点点睛:本题主要考查了立体几何中线面角的最值,解题的关键在于通过辅助线作出线面角,并求线面角的最值,空间思维能力较强,容易混淆.
变式6.(2024高二下·天津南开·学业考试)如图,在正方体ABCD-A1B1C1D1中,
(1)求证:平面AB1C//平面A1C1D;
(2)求直线AB1和平面BDD1B1所成角.
【答案】(1)证明见解析
(2)30°
【分析】(1)在正方体ABCD-A1B1C1D1中,可得A1D//B1C,则得A1D//平面AB1C,同理A1C1//平面AB1C,所以得平面AB1C//平面A1C1D;
(2)在正方体ABCD-A1B1C1D1中,可得AC⊥平面BDD1B1,则得∠AB1O为直线AB1和平面BDD1B1所成角,则在Rt△AB1O中,AB1=2AO,即可的∠AB1O=30°.
【详解】(1)在正方体ABCD-A1B1C1D1中,
因为A1B1//CD,A1B1=CD,所以四边形A1B1CD是平行四边形,
所以A1D//B1C,
又因为A1D⊄平面AB1C,B1C⊂平面AB1C,
所以A1D//平面AB1C,
同理,A1C1//平面AB1C,
又A1D∩A1C1=A1,
所以平面AB1C//平面A1C1D.
(2)
设AC∩BD=O,连接OB1,
因为BB1⊥平面ABCD,所以BB1⊥AC,
又因为AC⊥BD,BB1∩BD=B,BB1、BD⊂平面BDD1B1,
所以AC⊥平面BDD1B1,
所以B1O为AB1在平面BDD1B1的射影,
则∠AB1O为直线AB1和平面BDD1B1所成角,
设正方体的棱长为a,
则在Rt△AB1O中,AB1=2AO=2a,
所以∠AB1O=30°.
变式7.(24-25高二·上海·假期作业)已知斜三棱柱ABC-A'B'C'的底面是正三角形,侧棱AA'⊥BC,并且与底面所成角是60°.设侧棱长为l
(1)求此三棱柱的高;
(2)求证:侧面BB'C'C是矩形;
(3)求证:A'在平面ABC上的射影O在∠BAC的平分线上.
【答案】(1)32l
(2)证明见解析
(3)证明见解析
【分析】(1)利用线面角的定义和性质求解即可;
(2)利用斜三棱柱的性质结合平行关系求解即可;
(3)利用线线垂直、线面垂直的性质和判定定理求解即可.
【详解】(1)因为侧棱AA'与底面所成角是60°,且AA'=l,
则过A'点斜三棱柱的高h=AA'×sin60°=32l;
(2)因为斜三棱柱ABC-A'B'C',
所以侧面BB'C'C是平行四边形,AA'//BB',
又因为AA'⊥BC,所以BB'⊥BC,
所以平行四边形BB'C'C是矩形;
(3)过A点作∠BAC的平分线的平分线交BC于D,
过A'作A'O⊥AD交AD于O,
因为△ABC是正三角形,所以BC⊥AD,
又因为BC⊥AA',AA'∩AD=A,AA',AD⊂面AA'O,
所以BC⊥面AA'O,
因为A'O⊂面AA'O,所以BC⊥A'O,
因为BC∩AD=D,BC,AD⊂面ABC,
所以A'O⊥面ABC,即A'在平面ABC上的射影O在∠BAC的平分线AD上.
【方法技巧与总结】
计算线面角,一般有如下几种方法:
(1)利用面面垂直的性质定理,得到线面垂直,进而确定线面角的垂足,明确斜线在平面内的射影,即可确定线面角;
(2)在构成线面角的直角三角形中,可利用等体积法求解垂线段的长度h,从而不必作出线面角,则线面角θ满足sinθ=hl(l为斜线段长),进而可求得线面角;
(3)建立空间直角坐标系,利用向量法求解,设a为直线l的方向向量,n为平面的法向量,则线面角θ的正弦值为sinθ=csa,n.
【题型2:向量法求直线与平面所成的角】
例2.(23-24高二下·河南漯河·期末)已知如图所示的几何体中,底面ABC是边长为4的正三角形,侧面AA1C1C是长方形,AA1=6,平面AA1C1C⊥平面ABC,D为棱CC1上一点,CD=13CC1,且CD=12BB1,则B1D与平面AA1C1C所成角的正弦值为( )
A.35B.105C.255D.155
【答案】D
【分析】分别取A1C1,AC的中点E,O,以O为原点,OA,OB,OE所在的直线分别为x,y,z轴建立空间直角坐标系,求出平面AA1C1C的一个法向量,由线面角的向量求法可得答案.
【详解】分别取A1C1,AC的中点E,O,连接EO,BO,则EO//C1C,EO⊥AC,BO⊥AC,
因为平面AA1C1C⊥平面ABC,平面AA1C1C∩平面ABC=AC,
EO⊂平面AA1C1C,所以EO⊥平面ABC,
以O为原点,OA,OB,OE所在的直线分别为x,y,z轴建立空间直角坐标系,
则OB=23,CD=2,BB1=4,
所以OB=0,23,0是平面AA1C1C的一个法向量,
B10,23,4,D-2,0,2,所以DB1=2,23,2,
设B1D与平面AA1C1C所成的角为θ,
则sinθ=csDB1,OB=DB1⋅OBDB1⋅OB=1223×4+12+4=155.
故选:D.
变式1.(23-24高二下·江苏徐州·期中)如图,四边形ABCD,AB=BD=DA=4,BC=CD=22,现将△ABD沿BD折起,当二面角A-BD-C的大小在[π6,π3]时,直线AB和CD所成角为α,则csα的最大值为( )
A.22-616B.28C.22+616D.68
【答案】B
【分析】取BD中点O,连结AO,CO,以O为原点,OC为x轴,OD为y轴,过点O作平面BCD的垂线为z轴,建立空间直角坐标系,利用向量法能求出直线AB与CD所成角的余弦值的最大值.
【详解】取BD中点O,连接AO,CO,AB=BD=DA=4,BC=CD=22,
则CO⊥BD,AO⊥BD,且CO=2,AO=23,于是∠AOC是二面角A-BD-C的平面角,
显然BD⊥平面AOC,在平面AOC内过点O作Oz⊥OC,则BD⊥Oz,
直线OC,OD,Oz两两垂直,以O为原点,直线OC,OD,Oz分别为x,y,z轴建立空间直角坐标系,
B(0,-2,0),C(2,0,0),D(0,2,0),设二面角A-BD-C的大小为θ,θ∈[π6,π3],
因此A(23csθ,0,23sinθ),BA=(23csθ,2,23sinθ),CD=(-2,2,0),
于是csα=|cs⟨BA⃗,CD⃗⟩|=|BA⃗⋅CD⃗||BA⃗||CD⃗|=4-43csθ4×22=|1-3csθ|22,
显然csθ∈[12,32],则当csθ=32时,(csα)max=28,
所以csα的最大值为28.
故选:B
【点睛】关键点点睛:建立空间直角坐标系,求出动点A的坐标,利用向量建立函数关系是解题的关键.
变式2.(23-24高二下·江苏常州·阶段练习)如图,已知点A是圆台O1O的上底面圆O1上的动点,B,C在下底面圆O上,AO1=1,OO1=2,BO=3,BC=25,则直线AO与平面O1BC所成角的正弦值的最大值为 .
【答案】31010
【分析】以O为坐标原点,建立空间直角坐标系,求得对应点的坐标,设出未知点的坐标,利用向量法求线面角正弦值的最大值,再求余弦值的最小值即可.
【详解】解:连接OC,过C点作CH垂直于BO的延长线于点H,以O为坐标原点,建立空间直角坐标系如下所示:
在三角形OBC中,因为OB=3,OC=3,BC=25,
故csB=OB2+BC2-OC22OB⋅BC=9+20-92×3×25=53,
则BH=BC⋅csB=25×53=103,
则CH=BC2-BH2=20-1009=453,
OH=BH-OB=13,
故点C-13,453,0,又O(0,0,0),O1(0,0,2),B(3,0,0),
设点A(m,n,2),m,n∈-1,1,由O1A=1,可得m2+n2=1,
BC=-103,453,0,BO1=-3,0,2,
设平面O1BC的法向量m=x,y,z,
则m⋅BC=0m⋅BO1=0,即-103x+453y=0-3x+2z=0,
取y=5,则x=2,z=3,
故平面O1BC的法向量m=2,5,3,
又OA=m,n,2,
设直线AO与平面O1BC所成角为θ,θ∈0,π2,
则sinθ=csOA,m=m⋅OAmOA=2m+5n+632×m2+n2+4=2m+5n+6310,
因为m,n∈-1,1,且m2+n2=1,
故令m=csα,n=sinα,α∈(0,2π),
则2m+5n+6=5sinα+2csα+6=3sinα+φ+6,tanφ=255,φ∈-π2,π2,
又α∈(0,2π),所以sin(α+φ)∈-1,1,
∴3sin(α+φ)+6∈3,9,即2m+5n+6∈3,9,
所以sinθ的最大值为9310=31010.
故答案为:31010.
变式3.(贵州省黔东南州2023-2024学年高二下学期期末教学质量检测数学试题)如图,在正四棱柱ABCD-A1B1C1D1中,AA1=2AB=4,E,F分别为BB1,CC1的中点.
(1)证明:A1F//平面CDE.
(2)求A1E与平面CDE所成角的正弦值.
【答案】(1)证明见解析
(2)12
【分析】(1)借助正四棱柱的性质可建立空间直角坐标系,求出空间向量A1F与平面CDE的法向量后,借助空间向量计算即可得;
(2)求出空间向量A1E与平面CDE的法向量后,借助空间向量夹角公式计算即可得.
【详解】(1)在正四棱柱ABCD-A1B1C1D1中,AB,AD,AA1两两垂直,且AA1=2AB=4,
以A为坐标原点,AB,AD,AA1所在直线分别为x轴,y轴,z轴,
建立如图所示的空间直角坐标系,则C2,2,0,D0,2,0,A10,0,4.
因为E,F分别为BB1,CC1的中点,所以E2,0,2,F2,2,2,
则CD=-2,0,0,CE=0,-2,2,A1F=2,2,-2,
设平面CDE的法向量为m=x,y,z,
则CD⋅m=0CE⋅m=0,即-2x=0-2y+2z=0,
令y=1,则有x=0,z=1,即m⃗=0,1,1,
因为A1F⋅m=2×0+2×1+-2×1=0,所以A1F⊥m,
又A1F⊄平面CDE,所以A1F//平面CDE;
(2)由(1)可知,A1E=2,0,-2,
csA1E,m=A1E⋅mA1Em=-22×22=-12,
所以A1E与平面CDE所成角的正弦值为12.
变式4.(23-24高二下·广东·期末)如图,在三棱柱ABC-A1B1C1中,侧棱AA1⊥底面ABC,底面△ABC是正三角形,AB=AA1=3,点E、F分别在AB、A1C1上,且AE=13AB,C1F=13A1C1.
(1)求证:A1E//平面BCF;
(2)求直线BB1与平面BCF所成角的余弦值.
【答案】(1)证明见解析
(2)23913⋅
【分析】(1)在线段BC上取一点G,使CG=13BC,连结EG、FG,先证四边形A1FGE为平行四边形,所以A1E∥FG,从而可得A1E//平面BCF;
(2)以B为坐标原点,Bx,BC,BB1所在直线分别为x,y,z轴建立如图空间直角坐标系,利用线面角的空间向量法求解.
【详解】(1)在线段BC上取一点G,使CG=13BC,连结EG、FG,
在△ABC中,因为AE=13AB,CG=13BC,所以BEAB=BGBC=23,
所以EG∥AC且EG=23AC,
因为C1F=13A1C1,A1C1//AC,且A1C1=AC,
所以A1F∥AC,且A1F=23AC,
所以EG∥A1F且EG=A1F,
故四边形A1FGE为平行四边形,所以A1E∥FG,
又A1E⊄平面BCF,FG⊂平面BCF, 所以A1E∥平面BCF.
(2)以B为坐标原点,Bx,BC,BB1所在直线分别为x,y,z轴建立如图空间直角坐标系,
因为底面DABC是正三角形,AB=AA1=3,所以点B0,0,0,点C0,3,0,
点A332,32,0,点B10,0,3,点C10,3,3,
因为C1F=13CA,所以点F32,52,3,
则BC=0,3,0,BF=32,52,3,BB1=0,0,3,
设平面BCF的一个法向量为n=x,y,z.
由n⋅BC=3y=0n⋅BF=32x+52y+3z=0,令z=-3,
得平面BCF的一个法向量为n=6,0,-3,
设直线BB1与平面BCF所成角的大小为θ,
则sinθ=BB1⋅nBB1n=0,0,3⋅6,0,-33×39=1313,
所以csθ=1-sin2θ=1-13132=23913,
所以直线BB1与平面BCF所成角的余弦值为23913⋅
变式5.(贵州省六盘水市2023-2024学年高二下学期7月期末数学试题)已知长方体ABCD-A1B1C1D1中,AB=BC=1,AA1=2.
(1)在长方体中,过点C1作与平面AB1D1平行的平面α,并说明理由;
(2)求直线B1D与平面α所成角的正弦值.
【答案】(1)答案见解析;
(2)69.
【分析】(1)作图,即平面BDC1∥平面AB1D1求解;
(2)方法1,以点D为坐标原点建系,利用直线与平面的向量运算求解;
方法2,由体积公式求解.
【详解】(1)解:如图,所作平面α为平面BDC1.
理由如下:
因为ABC1D1为平行四边形,所以BC1∥AD1,
而BC1⊄平面AB1D1,AD1⊂平面AB1D1,得BC1∥平面AB1D1,
同理得DC1∥平面AB1D1,
而BC1∩DC1=C1,BC1,DC1⊂平面BDC1,
所以平面BDC1∥平面AB1D1.
(2)方法1:以点D为坐标原点建系如图,则B11,1,2,B1,1,0,C10,1,2.
DB1=1,1,2,DB=1,1,0,DC1=0,1,2,
设平面BDC1的法向量为m=x,y,z,则
m⋅DB=0m⋅DC1=0,即x+y=0y+2z=0,
令z=1,则y=-2,x=2,所以m=2,-2,1,
设B1D与平面BDC1所成的角为θ,则sinθ=cs
方法2:设点B1到平面BDC1的距离为d,
依题B1D=6,DC=1,S△BDC1=32,S△BB1C1=1,
因为VB1-BDC1=VD-BB1C1,所以13×d×S△BDC1=13×DC×S△BB1C1,
从而13×d×32=13×1×1,解得d=23,
设B1D与平面BDC1所成的角为θ,则sinθ=dB1D=69.
变式6.(23-24高二下·广东广州·期末)如图,在五棱锥P-ABCDE中,PA⊥平面ABCDE,AE//BC,AB//CD,AC//ED,∠ABC=45∘,AB=22,BC=2AE=4.
(1)求证:平面PCD⊥平面PAC;
(2)已知直线PB与平面PCD所成的角为30∘,求线段PA的长.
【答案】(1)证明见解析
(2)22
【分析】(1)由余弦定理得AC⊥AB,再由线面垂直的判定定理可得答案;
(2)做NE⊥AC交AC于点N,以A为原点,AP,AB,AC所在的直线分别为x,y,z建立空间直角坐标系,设AP=tt>0,求出BP、平面PCD的一个法向量,由线面角的向量求法求出t可得答案,
【详解】(1)∠ABC=45∘,AB=22,BC=4.
由余弦定理得AC2=AB2+BC2-2AB×BCcs45∘
=8+16-2×22×4×22=8,
所以AC2+AB2=BC2,故AC⊥AB,
因为AB//CD,所以AC⊥CD,
因为PA⊥平面ABCDE,CD⊂平面ABCDE,所以PA⊥CD,
因为AC∩PA=A,AC、PA⊂平面PAC,所以CD⊥平面PAC,
因为CD⊂平面PCD,所以平面PCD⊥平面PAC;
(2)做NE⊥AC交AC于点N,所以四边形ENCD是长方形,
因为AE//BC,∠BCA=45∘,所以∠NAE=45∘,
因为AE=2,所以CD=NE=2,
由(1)知,AP,AB,AC互相垂直,以A为原点,
AB,AC,AP所在的直线分别为x,y,z轴建立空间直角坐标系,
设AP=tt>0,则P0,0,t,B22,0,0,C0,22,0,D-2,22,0,
BP=-22,0,t,PC=0,22,-t,PD=-2,22,-t,
设n=x,y,z为平面PCD的一个法向量,
则n⋅PC=0n⋅PD=0,即22y-tz=0-2x+22y-tz=0,令y=2,则z=4t,x=0,
所以n=0,2,4t,
所以sin30∘=csn,BP=n⋅BPn⋅BP=42+16t2×8+t2=12,
解得t=22,所以P0,0,22,A0,0,0,
所以线段PA的长为22.
变式7.(23-24高二下·甘肃兰州·期末)如图,在Rt△AOB中,∠AOB=π2,AO=4,BO=2,Rt△AOC可以通过Rt△AOB以直线AO为轴旋转得到,且二面角B-AO-C是直二面角.动点D在线段AB上.
(1)当D为AB的中点时,求异面直线AO与CD所成角的余弦值;
(2)求CD与平面AOB所成角的正弦值的最大值.
【答案】(1)23
(2)53
【分析】(1)建立空间直角坐标系,利用空间向量求异面直线夹角;
(2)设BD=λBA可得D0,21-λ,4λ,利用空间向量求线面夹角结合二次函数分析运算.
【详解】(1)由题意可得:AO⊥OB,AO⊥OC,平面AOB⊥平面AOC,
平面AOB∩平面AOC=AO,OB⊂平面AOB,所以OB⊥平面AOC,
如图,以O为坐标原点建立空间直角坐标系,
则O0,0,0,A0,0,4,C2,0,0,B0,2,0,
若D为AB的中点,则D0,1,2,可得OA=0,0,4,CD=-2,1,2,
设异面直线AO与CD所成角θ,θ∈0,π2,
则csθ=csOA,CD=OA⋅CDOA⋅CD=84×3=23.
故异面直线AO与CD所成角的余弦值为23.
(2)若动点D在线段AB上,设Dx,y,z,BD=λBA,λ∈0,1,
则BD=x,y-2,z,BA=0,-2,4,可得x=0y-2=-2λz=4λ,解得x=0y=21-λz=4λ,
即D0,21-λ,4λ,则CD=-2,21-λ,4λ,
由题意可知:平面AOB的法向量为n=1,0,0,
设CD与平面AOB所成角为α,α∈0,π2,
则sinα=csn,CD=n⋅CDn⋅CD=24+41-λ2+16λ2=15λ2-2λ+2,
对于函数y=5λ2-2λ+2,开口向上,对称轴为λ=15∈0,1,
可得当λ=15时,y=5λ2-2λ+2取到最小值ymin=5×152-2×15+2=95,
所以sinα的最大值为195=53,因为α∈0,π2,
故CD与平面AOB所成角的正弦最大值为53.
变式8.(23-24高二下·广东·期末)如图,四棱锥P-ABCD的侧面PCD为正三角形,底面ABCD为梯形,AB//CD,平面PCD⊥平面ABCD,已知CD=4AB=4,PM=13MD.
(1)证明:AM //平面PBC;
(2)若AC=AD,PA=32,求直线AM与平面PAB所成角的正弦值.
【答案】(1)证明见解析
(2)1326
【分析】(1)取PC上的点N,使PN=14PC,可得MN=AB,则由线线平行可证线面平行;
(2)取CD中点O,连AO,PO,根据题意可证AO⊥CD,PO⊥平面ABCD,所以以O为坐标原点,OA,OC,OP分别为x,y,z轴正方向,建立如图所示空间直角坐标系A-xyz,利用线面角的空间向量法求解.
【详解】(1)取PC上的点N,使PN=14PC,
则MN=PN-PM=14PC-PD=14DC=AB,
所以四边形ABNM为平行四边形,所以AM//BN,
又BN⊂平面PBC,AM⊄平面PBC,所以AM //平面PBC;
(2)取CD中点O,连AO,PO,因为AC=AD,所以AO⊥CD,
因为△PCD为正三角形,所以PO⊥CD,PO=23,
又平面PCD⊥平面ABCD,平面PCD∩平面ABCD=CD,PO⊂平面PCD,
所以PO⊥平面ABCD,
因为AO⊂平面ABCD,所以PO⊥AO,AO=PA2-PO2=6,
以O为坐标原点,OA,OC,OP分别为x,y,z轴正方向,建立如图所示空间直角坐标系A-xyz,
则A(6,0,0),C(0,2,0),D(0,-2,0),B(6,1,0),P(0,0,23),
则AB=(0,1,0),PA=(6,0,-23),AM=AP+14PD=-6,-12,332,
设n=(x,y,z)为平面PAB的法向量,
则n⋅AB=0n⋅PA=0⇒y=06x-23z=0,可取n=2,0,1,
,故直线AM与平面PAB所成角的正弦值为1326.
【方法技巧与总结】
求线面角的两种思路
(1)线面角转化为线线角.根据直线与平面所成角的定义,确定出待求角,转化为直线的夹角来求解,此时要注意两直线夹角的取值范围.
(2)向量法.
方法一:设直线PA的方向向量为a,平面α的法向量为n,直线PA与平面α所成的角为 θ(θ∈[0,π2]),α与n的夹角为φ,则sin θ=lcs φ|=|an||a||n|
方法二:设直线PA的方向向量为a,直线PA在平面α内的投影的方向向量为b,
则直线PA与平面α所成的角θ满足csθ=|cs
【题型3:动点探索性习题】
例3.(多选)(2024·吉林·模拟预测)如图,在棱长为1的正方体ABCD-A1B1C1D1中,M,N分别是AB,AD的中点,P为线段C1D1上的动点,则下列说法正确的是( )
A.PM,B1C一定是异面直线
B.存在点P,使得MN⊥PM
C.直线NP与平面BCC1B1所成角的正切值的最大值为5
D.过M,N,P三点的平面截正方体所得截面面积的最大值为334
【答案】AD
【分析】对ABC选项,以D为坐标原点建立空间直角坐标系,利用向量法求解和判断即可;对D选项,由正方体的性质可得截面面积最大的状态,画出截面图,求得面积即可判断.
【详解】以D为坐标原点建立如图所示空间直角坐标系:
则B11,1,1,C0,1,0,M1,12,0,N12,0,0,
设D1P=m,m∈[0,1],则P点坐标为(0,m,1);
对A:设平面MB1C的法向量为n=(x,y,z),CM=1,-12,0,CB1=(1,0,1),
则n⋅CM=0n⋅CB1=0,即x-12y=0x+z=0,取y=2,解得x=1,z=-1,故n=(1,2,-1);
又MP=(-1,m-12,1),MP⋅n=-1+2m-12-1=2m-3,
考虑到m∈[0,1],则MP⋅n∈[-3,-1],故MP⋅n≠0,
故PM,B1C一定是异面直线,A正确;
对B:MP=(-1,m-12,1),MN=(-12,-12,0),
若MN⊥PM,则MP⋅MN=0,即12-12m-12=0,
解得m=32,又m∈[0,1],故不存在这样的点P,使得MN⊥PM,B错误;
对C: NP=(-12,m,1),取平面BCC1B1的法向量m=(0,1,0),
则cs
设直线NP与平面BCC1B1的夹角为θ,θ∈[0,π2]
则sinθ=mm2+54,则csθ=1-sin2θ=1-m2m2+54=52m2+54,
tanθ=sinθcsθ=255m,又m∈[0,1],故tanθ∈[0,255],
即直线NP与平面BCC1B1所成角的正切值的最大值为255,C错误;
对D:在正方体中,过M,N的截面为六边形且六边形为正六边形时面积最大.
此时过MN的截面经过对称中心O,
设截面交DD1,BB1,B1C1于中点,P也为中点,
所以P为C1D1的中点时,过M,N,P三点的平面截正方体所得截面面积最大,
取D1D,B1C1,BB1的中点为E,F,G,连接NE,EP,PF,FG,GM,如下所示:
故此时截面为正六边形MNEPFG,
其面积S=6×34MN2=6×34×12=334,故D正确.
故选:AD.
【点睛】关键点点睛:本题A选项解决的关键是能够掌握用向量法证明异面直线的方法;本题D选项解决的关键是能够合理转化问题,类比解决,从而找到截面面积最大的状态.
变式1.(多选)(2024·吉林长春·模拟预测)已知四棱锥P-ABCD,底面ABCD是正方形,PA⊥平面ABCD,AD=1,PC与底面ABCD所成角的正切值为22,点M为平面ABCD内一点(异于点A),且AM<1,则( )
A.存在点M,使得CM⊥平面PAB
B.存在点M,使得直线PB与AM所成角为π3
C.当AM=12时,三棱锥P-BCM的体积最大值为14
D.当AM=22时,以P为球心,PM为半径的球面与四棱锥P-ABCD各面的交线长为2+64π
【答案】BCD
【分析】利用反证法即可判断A;建立如图空间坐标系,利用空间向量法求解线线角即可判断B;确定S△BCM的最大值即可求解棱锥P-BCM的体积的最大值,即可判断C;通过展开图确定球体与侧面交线的长度,加上底面交线长即可判断D.
【详解】A:假设存在点M使得CM⊥平面PAB,由PA⊥平面ABCD,PA⊂平面PAB,
得平面PAB ⊥平面ABCD,又平面PAB ∩平面ABCD =AB,CM⊂平面ABCD,
则CM⊥AB,又CB⊥AB,CM,CB⊂平面ABCD,所以CM,CB重合,
即点M落在CB上,由AM<1,知点M落在以A为圆心,以AB=1为半径的圆面内(不含圆),
这与点M落在CB上矛盾,故A错误;
B:以A为原点,AB,AD,AP所在直线为x,y,z轴建立空间直角坐标系,
PA⊥平面ABCD,则∠PCA即为PC与底面ABCD所成的角,
故tan∠PCA=PAAC=22,而AC=2,所以PA=1,
则P(0,0,1),B(1,0,0),所以PB=(1,0,-1),结合A的分析,取AM=(12,12,0),
所以csPB,AM=PB⋅AMPBAM=122⋅22=12,又PB,AM∈(0,π2],
所以直线PB与AM所成角为π3,即存在点M使得直线PB与AM所成角为π3,故B正确;
C:当AM=12时,当M位于BA的延长线时,△BCM的高最大为32,
此时面积取得最大值12⋅1⋅32=34,所以三棱锥P-BCM的体积最大值为13⋅34⋅1=14,故C正确;
D:当AM=22时,PM=(22)2+12=62,
以P为球心,PM为半径的球面与四棱锥P-ABCD各面的交线
是以P为圆心,62为半径的圆与侧面展开图的交线,如下图EMF,
由PB=2,PC=3,有PC2=PB2+BC2,则PB⊥BC,
所以tan∠APF=22=tan∠BPC=12,则∠APF=∠BPC,∠APF+∠FPB=π4,
所以∠FPC=∠BPC+∠FPB=π4,根据对称性有∠FPC=∠CPE,
所以∠FPE=π2,故EMF的长为14⋅2π⋅62=6π4,
又球与底面ABCD的交线是以P为圆心,22为半径的的四分之一圆,其长度为14⋅2π⋅22=24π,
故P为球心,PM为半径的球面与四棱锥P-ABCD各面的交线长2+64π,故D正确.
故选:BCD
【点睛】难点点睛:本题考查了几何体中求解空间角以及体积和侧面展开图的问题,难度较大,难点在于D选项的判断,解答时要利用侧面展开图求解.
变式2.(多选)(23-24高二下·重庆·阶段练习)如图,在正方体ABCD-A1B1C1D1中,点P满足BP=λBC1,λ∈0,1,则下列结论正确的是( )
A.对于任意的λ,都有A1P//平面ACD1
B.对于任意的λ,都有A1P⊥B1D
C.若A1P⊥BC,则λ=0
D.存在λ,使A1P与平面BCC1B1所成的角为30°
【答案】ABC
【分析】
建立空间直角坐标系,利用空间位置关系的向量证明及线面角的向量求法求解判断即可.
【详解】在正方体ABCD-A1B1C1D1中,建立如图所示的空间直角坐标系,令AB=1,
则D(0,0,0),A(1,0,0),B(1,1,0),C(0,1,0),A1(1,0,1),B1(1,1,1),C1(0,1,1),D1(0,0,1),
由BP=λBC1=(-λ,0,λ),得P(1-λ,1,λ),A1P=(-λ,1,λ-1),
对于A,DB1=(1,1,1),AC=(-1,1,0),AD1=(-1,0,1),显然DB1⋅AC=0,DB1⋅AD1=0,
即DB1⊥AC,DB1⊥AD1,而AC∩AD1=A,AC,AD1⊂平面ACD1,则DB1⊥平面ACD1,
因此DB1=(1,1,1)是平面ACD1的法向量,又DB1⋅A1P=-λ+1+λ-1=0,
A1P⊄平面ACD1,所以A1P//平面ACD1,A正确;
对于B,由选项A知,对于任意的λ,DB1⋅A1P=0,即A1P⊥B1D,B正确;
对于C,由A1P⊥BC,BC=(-1,0,0),得A1P⋅BC=λ=0,C正确;
对于D,平面BCC1B1的法向量n=(0,1,0),令A1P与平面BCC1B1所成的角为θ,
则sinθ=|cs〈A1P,n〉|=1λ2+1+(λ-1)2=12(λ-12)2+32∈[22,63],
而sin30°=12∉[22,63],因此不存在λ,使A1P与平面BCC1B1所成的角为30°,D错误.
故选:ABC
变式3.(多选)(23-24高二上·河北邯郸·期中)在正四棱柱ABCD-A1B1C1D1中,AB=1,AA1=2,M,N分别为棱BB1,AD上的一点,则下列说法正确的是( )
A.AC⊥BD1
B.当M,N分别为棱BB1,AD的中点时,直线DM与D1N所成角的余弦值为5117
C.存在点M,使得∠A1MD为钝角
D.直线BD1与平面A1BN所成角的正弦值的取值范围是69,66
【答案】ABD
【分析】根据题意,建立空间直角坐标系,结合空间向量的坐标运算,对选项逐一判断,即可得到结果.
【详解】
以D为坐标原点,DA,DC,DD1所在的直线分别为x轴,y轴,z轴,建立空间直角坐标系,如图所示,由A(1,0,0),C(0,1,0),B(1,1,0),D1(0,0,2),有AC=(-1,1,0),BD1=(-1,-1,2),AC⋅BD1=0,可得AC⊥BD1,故A正确;
当M,N分别为棱BB1,AD的中点时,M(1,1,1),N12,0,0,D(0,0,0),D1(0,0,2),所以DM=(1,1,1),ND1=-12,0,2,所以DM=(1,1,1),ND1=-12,0,2,csDM,ND1=DM⋅ND1DM⋅ND1=321+1+1×14+4=5117,故B正确;
A1(1,0,2),设M(1,1,x),(0≤x≤2),所以A1M=(0,1,x-2),DM=(1,1,x),
所以A1M⋅DM=(0,1,x-2)⋅(1,1,x)=x2-2x+1=(x-1)2≥0,故C错误;
设N(y,0,0)(0≤y≤1),所以BN=(y-1,-1,0),BA1=(0,-1,2),设平面A1BN的一个法向量为n=(a,b,c),所以n⋅BN=(y-1)a-b=0,n⋅BA1=-b+2c=0,令a=1,解得b=y-1,c=y-12,所以平面A1BN的一个法向量为n=1,y-1,y-12,又BD1=(-1,-1,2),设直线BD1与平面A1BN所成角的大小为θ,所以sinθ=csn,BD1=n⋅BD1n⋅BD1=16×1+54(y-1)2,又0≤y≤1,所以sinθ∈69,66,故D正确.
故选:ABD.
变式4.(23-24高三上·四川成都·期末)如图所示的几何体是由正方形ABCD沿直线AB旋转90°得到的,设G是圆弧CE的中点,H是圆弧DF上的动点(含端点),则下列结论不正确的是( )
A.存在点H,使得EH⊥BG
B.存在点H,使得EH//BD
C.存在点H,使得EH//平面BDG
D.存在点H,使得直线EH与平面BDG的所成角为30°
【答案】B
【分析】由题意将图形补全为正方体,ADMF-BCNE,对于A,根据EF⊥平面BCNE,当F,H重合即可判定;对于B,根据BD//平面EFMN,而H是圆弧DF上的动点,即可判定;对于C,建立空间直角坐标系,根据平面BDG的法向量和EH垂直即可判定结果;对于D,当点H与点F重合时,直线EH与平面BDG所成角最大,求出夹角正弦值,进一步分析即可.
【详解】对于A,因为正方体ADMF-BCMF中,EH⊥平面BCNE, BG⊂平面BCNE,所以
EF⊥BG,所以当F,H重合时,由EH⊥BG.由A正确;
对于B,因为BD//EM,若EH//BD,则EH//EM,又EH∩EM=E,所以B不正确;
对于C,以A为原点,AD,AF,AB为x,y,z轴的正方向建立空间直角坐标系,
设BC=2,则A0,0,0,D2,0,0,E0,2,2,F0,2,0,
B0,0,2,C2,0,2,G2,2,2,
Hm,n,0,m2+n2=4,m>0,n>0,
所以BD=2,0,-2,BG=2,2,0,EH=m,n-2,-2
设n=x,y,z为平面BDG的一个法向量,
则BD·n=0BG·n=0即2x+0-2z=02x+2y-0×z=0,
令x=1,得y=-1,z=1,则n=1,-1,1
假设EH//平面BDG,
则n·EH=m-n+2-2=0,所以m=n.
因为m2+n2=4,m>0,n>0,所以m=n=2,
即H是圆弧DF的中点,符合题意,故C正确;
对于D,当点H与点F重合时,直线EH与平面BDG所成角最大,
EF=BA=0,0,-2,
所以csn·EF=n·EFnEF=-223=-33.
由33>12,得直线EH与平面BDG的所成角的最大角大于30°,
所以存在点H,使得直线EH与平面BDG的所成角为30°,故D正确.
故选:B
变式5.(2024·四川南充·模拟预测)如图,四棱锥P-ABCD中,底面ABCD为矩形,点E在线段PA上,PC//平面BDE.
(1)求证:AE=PE;
(2)若△PAD是等边三角形,AB=2AD,平面PAD⊥平面ABCD,四棱锥P-ABCD的体积为93,试问在线段DE上是否存在点Q,使得直线BQ与平面PCD所成角的正弦值为3322?若存在,求出此时DQ的长;若不存在,请说明理由.
【答案】(1)证明见解析
(2)存在,938
【分析】(1)连接AC,设AC∩BD=O,连接EO,即可得到O为AC的中点,再由线面平行的性质得到PC//EO,即可得证;
(2)作PF⊥AD于F,即可得到PF⊥平面ABCD,根据锥体的体积求出a,再建立空间直角坐标,利用空间向量法计算可得.
【详解】(1)连接AC,设AC∩BD=O,连接EO.
因为ABCD为矩形,所以O为AC的中点,
因为PC//平面BDE,PC⊂平面PAC,平面PAC∩平面BDE=EO,
所以PC//EO.
因为O为AC的中点,所以E为PA的中点,所以AE=PE.
(2)设AD=aa>0,因为△PAD是等边三角形,所以PA=PD=a.
如图,作PF⊥AD于F,则PF=32a,
因为平面PAD⊥平面ABCD,PF⊥AD,PF⊂平面PAD,平面PAD∩平面ABCD=AD,
所以PF⊥平面ABCD,所以PF是四棱锥P-ABCD的高,
因为ABCD为矩形,AD=a,AB=2AD=2a,所以SABCD=AB×AD=2a2,
所以VP-ABCD=13SABCD⋅PF=13×2a2×32a=33a3=93,解得a=3.
因为ABCD为矩形,所以CD⊥AD,平面PAD⊥平面ABCD,CD⊂平面ABCD,
平面PAD∩平面ABCD=AD,所以CD⊥平面PAD,
建立如图所示空间直角坐标系,则D0,0,0,C0,6,0,P32,0,332,A3,0,0,E94,0,334,B3,6,0,
所以DC=0,6,0,DP=32,0,332,DE=94,0,334,
设平面PCD的一个法向量为n=x,y,z,则n⋅DC=6y=0n⋅DP=32x+332z=0,取n=-3,0,1,
假设在线段DE上存在点Q,使得直线BQ与平面PCD所成角θ的正弦值为3322,
设DQ=λDE0≤λ≤1,BD=-3,-6,0,
则BQ=BD+DQ=-3,-6,0+λ94,0,334=94λ-3,-6,334λ,
所以sinθ=csBQ,n=-394λ-3+334λ294λ-32+36+334λ2=3322,
化简得4λ2-19λ+12=0,解得λ=4(舍去)或λ=34,
因为DE=942+3342=332,此时DQ=34DE=938,
所以线段DE上存在点Q,使得直线BQ与平面PCD所成角θ的正弦值为3322,此时DQ的长为938.
变式6.(23-24高二上·山东青岛·期末)如图,在底面是菱形的四棱锥P-ABCD中,PA⊥底面ABCD,PA=AC=2,∠ABC=60°,E,F分别在梭PD,PC上,M为BC的中点.
(1)若PE=2DE,F为PC中点,证明:BF ∥面ACE;
(2)若PE=DE,是否存在点F,使得ME与平面AMF所成角的正弦值为15?若存在,求出PCPF的值;若不存在,请说明理由.
【答案】(1)证明见解析
(2)存在点F,且PCPF=2或PCPF=54
【分析】(1)建立空间直角坐标系,利用法向量证明线面平行即可;
(2)设PF=tPC0≤t≤1,利用向量法求出求出线面角的正弦,由正弦值得出参数,即可得解.
【详解】(1)∵PA=AC=2,∠ABC=60∘,所以△ABC为等边三角形,
∵M为BC中点,∴AM⊥BC,AM=22-12=3,
又AD ∥ BC,所以AM⊥AD
以A为原点,AM,AD,AP分别头x,y,z轴,建立空间直角坐标系,如图,
则B(3,-1,0),C(3,1,0),M(3,0,0),D(0,2,0),P(0,0,2),F32,12,1
∵PE=2DE,∴E0,43,23,
BF=-32,32,1,AC=3,1,0,AE=0,43,23
设平面ACE的一个法向量m=x,y,z,
则m⋅AC=0m⋅AE=0,∴3x+y=043y+23z=0,令x=1,可得m=1,-3,23,
∵BF⋅m=-32,32,1⋅1,-3,23=0,∴BF⊥m,
又∵BF⊄面ACE,∴BF ∥面ACE.
(2)设PF=tPC0≤t≤1,
则M3,0,0C3,1,0,P0,0,2,E0,1,1,F3t,t,2-2t,
∴AM=3,0,0,AF=3t,t,2-2t,ME=-3,1,1,
设平面AMF的法向量n=x,y,z,
则n⋅AM=0n⋅AF=0,即3x=03tx+ty+2-2tz=0,
令z=t,得平面AMF的一个法向量n=0,2t-2,t,
设ME与平面AMF所成的角为θ,
则sinθ=csME,n=ME⋅nMEn=2t-2+t5×(2t-2)2+t2=3t-25×5t2-8t+4=15,
解得t=12或t=45,
即存在点F,且PCPF=2或PCPF=54.
变式7.(23-24高二上·福建三明·期末)在如图所示的多面体ABCDEF中,四边形ABCD为菱形,且∠ADC为锐角.在梯形ABEF中,AF//BE,AF⊥AB,AB=BE=2AF=2,平面ABEF⊥平面ABCD.
(1)证明:BD⊥平面ACF;
(2)若VE-ABC=233,AG=λABλ∈0,1,是否存在实数λ,使得直线CG与平面CEF所成角的正弦值为64,若存在,则求出λ,若不存在,说明理由.
【答案】(1)证明见解析
(2)存在;λ=12
【分析】(1)利用面面垂直得到AF⊥平面ABCD,进而得到AF⊥BD,再结合线面垂直的判定定理证明即可;
(2)由VE-ABC=233可得∠ABC=π3,并建立空间直角坐标系,利用向量法表示出线面角,从而求得λ.
【详解】(1)因为平面ABEF⊥平面ABCD,AF⊥AB,AF⊂平面ABEF,
平面ABEF∩平面ABCD=AB,
所以AF⊥平面ABCD,
又因为BD⊂平面ABCD,所以AF⊥BD,
因为四边形ABCD为菱形,所以BD⊥AC,
又AF∩AC=A,AF,AC⊂平面ACF,所以BD⊥平面ACF,
(2)
设AC∩BD=O,取CF中点H,连接OH,
易得OH//AF,因为AF⊥平面ABCD,所以OH⊥平面ABCD,
因为VE-ABC=13S△ABC⋅BE=13⋅12BCBAsin∠ABC⋅2=43sin∠ABC=233,
所以sin∠ABC=32.
因为∠ADC为锐角,所以∠ABC=π3,所以△ABC为等边三角形,
所以AO=1,OB=3.
以O为原点,OC,OB,OH所在直线分别为x,y,z轴建立如图所示的空间直角坐标系,
则C1,0,0,F-1,0,1,E0,3,2,A-1,0,0,B0,3,0,
所以CF=-2,0,1,CE=-1,3,2,
设平面CEF的一个法向量n=x,y,z,则n⋅CF=0n⋅CE=0,
即-2x+z=0-x+3y+2z=0,
取x=1,可得z=2,y=-3,故n=1,3,2,
假设存在实数λ,使得直线CG与平面CEF所成角的正弦值为64,
C1,0,0,F-1,0,1,E0,3,2,A-1,0,0,B0,3,0,
设Gx,y,z,由AG=λABλ∈[0,1],得x+1,y,z=λ1,3,0,
即Gλ-1,3λ,0,则CG=λ-2,3λ,0.
设直线CG与平面CEF所成的角为θ,
则sinθ=csCG,n=CG⋅nCGn=2+2λ224λ2-4λ+4=64,
解得2λ2-5λ+2=0,即λ=2或λ=12,又因为λ∈0,1,所以λ=12,
故存在实数λ=12,使得直线CG与平面CEF所成角的正弦值为64.
变式8.(23-24高二上·广西柳州·开学考试)如图(1),在Rt△ABC中,∠BAC=90∘,CA=2AB=4,D,E分别是AC,BC的中点,将△CDE和△BAE分别沿着DE,AE翻折,形成三棱锥P-ADE,M是AD中点,如图(2).
(1)求证:PM⊥平面ADE;
(2)若直线PM上存在一点Q,使得QE与平面PAE所成角的正弦值为14,求QM的值.
【答案】(1)见解析
(2)QM=36
【分析】(1)根据线面平行的性质定理和判断定理,结合垂直关系,平行关系的转化,即可证明;
(2)根据(1)的结果,以点M为原点,建立空间直角坐标系,求平面PAE的法向量,利用线面角的向量法,即可求解.
【详解】(1)因为点D,E分别是AC,BC边的中点,所以DE//AB,
因为∠BAC=90∘,即AB⊥AC,所以DE⊥AC,
所以DE⊥AD,DE⊥CD,即DE⊥PD,
因为AD∩PD=D,AD,PD⊂平面PAD,
所以DE⊥平面PAD,又PM⊂平面PAD,所以PM⊥DE,
由题意,PA=BA=2,PD=CD=12CA=2,则PA=PD=2,
又M是AD的中点,所以PM⊥AD,
因为AD∩DE=D,AD,DE⊂平面ADE,
所以PM⊥平面ADE;
(2)
以M为原点,MD,MP分别为x,z轴,作My//DE,建立如图所示的空间直角坐标系,
由PA=PD=2,DE=12AB=1,
则A-1,0,0,D1,0,0,P0,0,3,E1,1,0,
PA=-1,0,-3,AE=2,1,0,
设平面PAE的法向量为n=x,y,z,
则n⋅PA=-x-3z=0n⋅AE=2x+y=0,令z=-1,则n=3,-23,-1,
设Q0,0,t,则QE=1,1,-t,
因为QE与平面PAE所成角的正弦值为14,
所以csQM,n=t-34×t2+2=14,解得:t=36,
则Q0,0,36,故QM=36.
一、单选题
1.(23-24高二上·福建南平·期末)已知直线l的一个方向向量为u=1,0,1,平面α的一个法向量为n=0,-1,1,则l与α所成角的正弦值为( )
A.12B.32C.22D.1
【答案】A
【分析】设出夹角θ,由,求出答案.
【详解】设l与α所成角的大小为θ,
则sinθ=csu,n=u⋅nu⋅n=1,0,1⋅0,-1,11+1×1+1=12.
故选:A
2.(22-23高一下·湖南·期末)在正方体ABCD-A1B1C1D1中,E为BC的中点,则直线D1E与平面ACD1所成的角的正弦值为( )
A.13B.39C.29D.19
【答案】B
【分析】建立空间直角坐标系,利用向量法求得直线D1E与平面ACD1所成角的正弦值.
【详解】设正方体的棱长为4,直线D1E与平面ACD1所成的角为α,
以DA,DC,DD1所在直线为x,y,z轴,建立空间直角坐标系,
B14,4,4,D10,0,4,A4,0,0,C0,4,0,E2,4,0,
AD1=-4,0,4,CD1=0,-4,4,
DB1⋅AD1=0,DB1⋅CD1=0,所以DB1⊥AD1,DB1⊥CD1,
由于AD1∩CD1=D1,所以DB1⊥平面ACD1,
即平面ACD1的法向量为DB1=4,4,4,D1E=2,4,-4,
所以sinα=D1E⋅DB1D1E⋅DB1=39.
故选:B
3.(23-24高三下·广东·阶段练习)如图,正方体ABCD-A1B1C1D1的边长为4,D1P=3PC1,平面α经过点A1,P,则( )
A.A1P⊥PC
B.直线A1P与直线BC所成角的正切值为34
C.直线A1P与平面ABB1A1所成角的正切值为43
D.若C∈α,则正方体截平面α所得截面面积为26
【答案】BC
【分析】本题四个选项逐个分析,A选项利用在△A1PC勾股定理判断;B,C选项分别作出线线角,线面角算出正切值判断是否正确;D选项面面平行的性质的定理画出完整的截面进而计算面积即可.
【详解】在ABCD-A1B1C1D1中,A1C=AA12+AB2+BC2=43,A1P=A1D12+D1P2=5
在△A1PC中,A1C=43,A1P=5,PC=17,
∵A1C2≠A1P2+CP2,∴A错误.
∵BC//B1C1//A1D1,∴直线A1P与直线BC所成角等于∠D1A1P,tan∠D1A1P=D1PD1A1=34,∴B正确.
因为平面ABB1A1 ∥ CDD1C1,且A1D1⊥平面CDD1C1
所以直线A1P与平面ABB1A1所成角等于直线A1P与平面CDD1C1所成角∠A1PD1,tan∠A1PD1=43,∴C正确.
因为正方体的对面都是相互平行,且根据面面平行的性质定理可得,
在AB边上作点Q使得BQ=3QA,则平行四边形A1PCQ为所求截面.
在△A1PC中cs∠A1CP=48+17-252×43×17=551,
∴sin∠A1CP=2651,S△A1PC=12×43×17×2651=226,
∴平行四边形A1PCQ的面积为426.∴D错误.
故选:BC
4.(23-24高二下·江苏常州·期中)已知四棱锥P-ABCD的底面为直角梯形,AB//DC,∠DAB=90° PA⊥底面ABCD,且PA=AD=DC=1,AB=2,则异面直线AC与PB所成的角的余弦值为( )
A.55B.105C.155D.255
【答案】B
【分析】建立空间直角坐标,利用空间向量法计算可得.
【详解】∵四棱锥P-ABCD的底面为直角梯形,AB//DC,∠DAB=90°,
PA⊥底面ABCD,且PA=AD=DC=1,AB=2,
∴以A为原点,AD为x轴,AB为y轴,AP为z轴,建立空间直角坐标系,
则A0,0,0,C1,1,0,P0,0,1,B0,2,0,
则AC=1,1,0,PB=0,2,-1,
设直线AC与PB所成角为θ,则csθ=AC⋅PBAC⋅PB=22×5=105,
∴直线AC与PB所成角的余弦值为105.
故选:B
5.(23-24高二上·北京·期中)如图,在正方体ABCD-A1B1C1D1中,点E是线段A1C1上任意一点,则AE与平面ABCD所成角的正弦值不可能是( )
A.22B.53C.55D.1
【答案】C
【分析】建立空间直角坐标系,利用空间向量法求出AE与平面ABCD所成角的余弦值范围,即可得出正弦值的范围.
【详解】以B为原点建立空间直角坐标系如图:设棱长为1,
则B0,0,0,A1,0,0,设Et,1-t,1,0≤t≤1,
所以AE=t-1,1-t,1,平面ABCD的法向量为BB1=0,0,1
csBB1,AE=BB1⋅AEBB1⋅AE=121-t2+1 ∈33,1,
所以则AE与平面ABCD所成角的正弦值取值范围为33,1.
对比各选项,C项不可能.
故选:C
6.(23-24高二上·河南郑州·期末)人教A版选择性必修第一册教材44页“拓广探索”中有这样的表述:在空间直角坐标系中,若平面α经过点P0x0,y0,z0,且以u=a,b,cabc≠0为法向量,设Px,y,z是平面α内的任意一点,由u⋅P0P=0,可得ax-x0+by-y0+cz-z0=0,此即平面的点法式方程.利用教材给出的材料,解决下面的问题:已知平面α的方程为2x+2y+z-7=0,直线l的方向向量为1,2,-2,则直线l与平面α所成角的正弦值为( )
A.659B.49C.53D.59
【答案】B
【分析】根据题意求出平面α的法向量,利用线面角公式即可求解.
【详解】因为平面α的方程为2x+2y+z-7=0,
所以平面α的一个法向量为m=(2,2,1),
直线l的方向向量为n=1,2,-2,
设直线l与平面α所成角为θ,
则sinθ=|cs
故选:B.
7.(23-24高二上·广西·期末)如图所示空间直角坐标系A﹣xyz中,Px,y,z是正三棱柱ABC-A1B1C1的底面A1B1C1内一动点,A1A=AB=2,直线PA和底面ABC所成的角为π3,则P点的坐标满足( )
A.x2+y2=43B.x2+y2=2
C.x2+y2=3D.x2+y2=4
【答案】A
【分析】写出各点坐标,求得平面法向量,利用线面角公式计算化简求得答案.
【详解】由正三棱柱ABC-A1B1C1,且A1A=AB=2,根据坐标系可得:A0,0,0,A10,0,2,又Px,y,z是正三棱柱ABC-A1B1C1的底面A1B1C1内一动点,则z=2,所以PA=-x,-y,-z,又AA1⊥平面ABC,所以AA1=0,0,2是平面ABC的一个法向量,因为直线PA和底面ABC所成的角为π3,
所以csPA,AA1=PA⋅AA1PA⋅|AA1|=-2zx2+y2+z2×2=zx2+y2+z2=32,整理得z2=3x2+3y2,又z=2,所以x2+y2=43.
故选:A.
8.(2024·陕西·模拟预测)在平行六面体ABCD-A1B1C1D1中,已知AB=AD=AA1=1,∠A1AB=∠A1AD=∠BAD=60°,则下列选项中错误的一项是( )
A.直线A1C与BD所成的角为90°
B.线段A1C的长度为2
C.直线A1C与BB1所成的角为90°
D.直线A1C与平面ABCD所成角的正弦值为63
【答案】D
【分析】在平行六面体ABCD-A1B1C1D1中,取AB=a,AD=b,AA1=c,利用空间向量的线性运算及数量积运算,逐一分析选项,即可得出答案.
【详解】在平行六面体ABCD-A1B1C1D1中,令AB=a,AD=b,AA1=c,
由AB=AD=AA1=1,∠A1AB=∠A1AD=∠BAD=60°,
得|a|=|b|=|c|=1,a⋅b=b⋅c=a⋅c=12,
对于A,显然A1C=a+b-c,BD=-a+b,
则A1C⋅BD=(a+b-c)⋅(-a+b)=-a2+b2+a⋅c-b⋅c=0,即A1C⊥BD,
因此直线A1C与BD所成的角为90°,A正确;
对于B,|A1C|2=(a+b-c)2=a2+b2+c2-2b⋅c=2,即A1C=2,B正确;
对于C,A1C⋅BB1=(a+b-c)⋅c=a⋅c+b⋅c-c2=0,即A1C⊥BB1,
因此直线A1C与BB1所成的角为90°,C正确;
对于D,在平行六面体ABCD-A1B1C1D1中,四边形ABCD是菱形,即AC⊥BD,
又A1C⊥BD,A1C∩AC=C,A1C,AC⊂平面A1CA,于是BD⊥平面A1CA,
又BD⊂平面ABCD,则平面A1CA⊥平面ABCD,
连接AC交BD于点O,在平面A1CA内过点A1作A1E⊥AC于点E,如图,
由平面A1CA∩平面ABCD=AC,因此A1E⊥平面ABCD,即直线A1C与平面ABCD所成角为∠A1CA,
AC=a+b,则AC|2=a+b|2=a2+b2+2a⋅b=3,即AC=3,
由AA1//BB1及选项C知,∠AA1C=90°,则sin∠A1CA=13=33,D错误.
故选:D
二、多选题
9.(23-24高二上·四川南充·阶段练习)在如图所示的直四棱柱ABCD-A1B1C1D1中,底面ABCD是边长为2的正方形,AA1=3.点M是侧面BCC1B1内的动点(不含边界),AM⊥MC,则A1M与平面BCC1B1所成角的正切值可以为( )
A.377B.277
C.3D.2
【答案】AD
【分析】根据题意确定M点的轨迹,利用线面角定义可得A1M与平面BCC1B1所成角即为∠A1MB1,利用圆的几何性质确定B1M的范围,即可求出线面角正切值的范围,从而得出正确选项.
【详解】由题意建系如图,
因为底面ABCD是边长为2的正方形,AA1=3,
则A(2,0,3),C(0,2,3),设M(x,2,z),
可得AM=(x-2,2,z-3),CM=(x,0,z-3),
由题意得AM⊥MC,故AM⋅CM=x(x-2)+(z-3)2=0,
可得(x-1)2+(z-3)2=1,
故M点轨迹是以N(1,2,3)为圆心,1为半径的圆在正方形BCC1B1内的部分(不含边界),
由题可知N(1,2,3)为BC的中点,如图,
根据圆的几何性质可得:
当N,M,B1共线时,B1M取得最小值为12+32-1=1,
而B1M
所以tan∠A1MB1=A1B1B1M=2B1M∈(277,2],
所以正确选项有AD.
故选:AD.
10.(23-24高二下·山西吕梁·阶段练习)如图,正方体ABCD-A1B1C1D1的棱长为3,E,F分别为棱BB1,DD1上的点,且BE=13BB1,DF=13DD1,平面AEF与棱CC1交于点G,若点P为正方体内部(含边界)的点,满足AP=λAE+μAF,λ,μ∈0,1,则( )
A.点P的轨迹为四边形AEGF及其内部
B.当λ=1时,点P的轨迹长度为10
C.当λ=0,μ=12时,AF⊥A1P
D.当μ=12时,直线AP与平面ABCD所成角的正弦值的最大值为2211
【答案】ABD
【分析】取CC1上一点H,使得CH=13CC1,证得四边形AEGF为平行四边形,结合空间向量基本定理可知,可判定A正确;当λ=1时,得到EP=μEG,得到P的轨迹长度为线段EG的长,可判定B正确;当λ=0,μ=12时,以D为坐标原点,建立空间直角坐标系,结合AF⋅A1P≠0,可判定C错误;当μ=12时,由MP=aMN,可得P32,3a,a+12,求得平面ABCD的一个法向量为m=0,0,1和AP=-32,3a,a+12,结合向量的夹角公式,以及二次函数的性质,即可求解.
【详解】对于A中,取CC1上一点H,使得CH=13CC1,连接EH,FH,HB,
可得AF//BH且AF=BH,GE//BH且GE=BH,
所以四边形AFHB和四边形BHGE是平行四边形,所以AF//EG,AF=EG,
所以四边形AEGF为平行四边形,
因为AP=λAE+μAF,由空间向量基本定理可知,所以P在四边形AEGF内(或边界上),所以A正确;
对于B中,当λ=1时,AP=AE+μAF,所以AP-AE=μEG,即EP=μEG,
所以P在线段EG上,点P的轨迹长度为线段EG的长,所以EG=AF=10,所以B正确;
对于C中,当λ=0,μ=12时,可得点P为线段AF的中点,
以D为坐标原点,建立如图所示的空间直角坐标系,
则A3,0,0,F0,0,1,E3,3,1,A13,0,3,可得P32,0,12,
则AF=-3,0,1,A1P=-32,0,-52,可得AF⋅A1P=92-52=2≠0,
所以AF⊥A1P不成立,所以C错误;
对于D中,当μ=12时,AP=λAE+12AF,分别取AF,EG的中点M,N,
连接MN,P在线段MN上,M32,0,12,N32,3,32,
由MP=aMN0≤a≤1,可得P32,3a,a+12,
平面ABCD的一个法向量为m=0,0,1,AP=-32,3a,a+12,
设AP与平面ABCD所成的角为θ,
所以sinθ=csAP,m=AP⋅mAP⋅m=a+1294+3a2+a+122,
设t=12a+1,因为a∈0,1,则t∈13,1,
则a=12t-12,代入可得sinθ=118t2-18t+10,
当t=12时,直线AP与平面ABCD所成角的正弦值的最大值为2211,所以D正确.
故选:ABD.
11.(23-24高二下·重庆·阶段练习)如图,在正方体ABCD-A1B1C1D1中,点P满足BP=λBC1,λ∈0,1,则下列结论正确的是( )
A.对于任意的λ,都有A1P//平面ACD1
B.对于任意的λ,都有A1P⊥B1D
C.若A1P⊥BC,则λ=0
D.存在λ,使A1P与平面BCC1B1所成的角为30°
【答案】ABC
【分析】
建立空间直角坐标系,利用空间位置关系的向量证明及线面角的向量求法求解判断即可.
【详解】在正方体ABCD-A1B1C1D1中,建立如图所示的空间直角坐标系,令AB=1,
则D(0,0,0),A(1,0,0),B(1,1,0),C(0,1,0),A1(1,0,1),B1(1,1,1),C1(0,1,1),D1(0,0,1),
由BP=λBC1=(-λ,0,λ),得P(1-λ,1,λ),A1P=(-λ,1,λ-1),
对于A,DB1=(1,1,1),AC=(-1,1,0),AD1=(-1,0,1),显然DB1⋅AC=0,DB1⋅AD1=0,
即DB1⊥AC,DB1⊥AD1,而AC∩AD1=A,AC,AD1⊂平面ACD1,则DB1⊥平面ACD1,
因此DB1=(1,1,1)是平面ACD1的法向量,又DB1⋅A1P=-λ+1+λ-1=0,
A1P⊄平面ACD1,所以A1P//平面ACD1,A正确;
对于B,由选项A知,对于任意的λ,DB1⋅A1P=0,即A1P⊥B1D,B正确;
对于C,由A1P⊥BC,BC=(-1,0,0),得A1P⋅BC=λ=0,C正确;
对于D,平面BCC1B1的法向量n=(0,1,0),令A1P与平面BCC1B1所成的角为θ,
则sinθ=|cs〈A1P,n〉|=1λ2+1+(λ-1)2=12(λ-12)2+32∈[22,63],
而sin30°=12∉[22,63],因此不存在λ,使A1P与平面BCC1B1所成的角为30°,D错误.
故选:ABC
三、填空题
12.(24-25高二上·上海·单元测试)如图,在正方体ABCD-A1B1C1D1中,O是AC中点,点P在线段A1C1上,若直线OP与平面A1BC1所成的角为θ,则sinθ的取值范围是 .
【答案】23,33
【分析】建立空间直角坐标系,利用向量法求得sinθ的取值范围.
【详解】设正方体边长为2,建立如图所示空间直角.则O1,1,0,A12,0,2,B2,2,0,C10,2,2,
设Pa,2-a,20≤a≤2,
则OP=a-1,1-a,2,A1B=0,2,-2,A1C1=-2,2,0,
由于n=1,1,1 使n⋅A1B=1,1,1⋅0,2,-2=0,n⋅A1C1=1,1,1⋅-2,2,0=0,
所以n=1,1,1是平面A1BC1的法向量,
所以sinθ=n⋅OPn⋅OP=a-1+1-a+23⋅2×a-12+22 =26×1a-12+2,
由于0≤a≤2,所以a-12+2∈2,3,1a-12+2∈33,22,
所以 sinθ=26×1a-12+2∈23,33,
故答案为:23,33
13.(23-24高二上·浙江·期中)如图,正四棱柱ABCD-A1B1C1D1中,设AD=1,DD1=3,点P在线段CC1上,且C1P=2PC,则直线A1P与平面PBD所成角的正弦值是 .
【答案】223/232
【分析】建立空间直角坐标系,求出平面的法向量,求出线面角的正弦值.
【详解】以D为坐标原点,DA,DC,DD1所在直线分别为x,y,z轴,建立空间直角坐标系,
则A11,0,3,P0,1,1,B1,1,0,D0,0,0,
设平面PBD的法向量为m=x,y,z,
则m⋅DP=x,y,z⋅0,1,1=y+z=0m⋅DB=x,y,z⋅1,1,0=x+y=0,
令y=1,则x=z=-1,故m=-1,1,-1,
设直线A1P与平面PBD所成角大小为θ,
则sinθ=csm,A1P=m⋅A1Pm⋅A1P=-1,1,-1⋅-1,1,-21+1+1×1+1+4=1+1+23×6=223,
故答案为:223
14.(24-25高二上·上海·单元测试)如图,在直三棱柱ABC-A1B1C1中,∠ABC=90°,BC=2,CC1=4,点D为CC1的中点,则B1D与平面ABD的位置是 .
【答案】垂直
【分析】建立空间直角坐标系,证明B1D⊥BD,B1D⊥BA,即可得B1D与平面ABD的位置关系.
【详解】如图所示,分别以BA,BC,BB1所在直线为x,y,z轴建立如图空间直角坐标系,
且BC=2,CC1=4.
设AB=a,则B1(0,0,4),B(0,0,0),A(a,0,0),D(0,2,2),
所以B1D→=(0,2,-2),BD→=(0,2,2),BA→=(a,0,0),
因为B1D→·BD→=0,B1D→·BA→=0,
所以B1D→⊥BD→,B1D→⊥BA→,
因为BD∩BA=B,BD⊂平面ABD,BA⊂平面ABD,
所以B1D⊥平面ABD.
故答案为:垂直.
四、解答题
15.(23-24高二下·安徽宣城·期末)如图,在四棱锥P-ABCD中,PA⊥平面ABCD,且AD ∥ BC,∠BAD=90∘,BC=1,AP=AB=3,∠ADC=60∘,M,N分别为棱PC,PB的中点.
(1)求证:平面PBC⊥平面ADMN;
(2)求直线BD与平面ADMN所成角的正弦值.
【答案】(1)证明见解析
(2)4214
【分析】(1)先证明PB⊥平面ADMN,根据面面垂直的判定定理即可证明结论;
(2)方法一:结合(1)可知PB⊥平面ADMN,即可说明∠BDN即为直线BD与平面ADMN所成的角,解三角形,即可求得答案;方法二,建立空间直角坐标系,求出相关点坐标,利用空间角的向量求法,即可求得答案.
【详解】(1)∵PA⊥平面ABCD,AD⊂平面ABCD,则PA⊥AD,
由∠BAD=90∘,则AD⊥AB;
又AB∩PA=A,AB,PA⊂平面PAB,
∴AD⊥平面PAB,PB⊂平面PAB,
∴AD⊥PB,
∵AP=AB,且N为PB的中点,
∴PB⊥AN,
∵AN∩AD=A,AN,AD⊂平面ADMN,
∴PB⊥平面ADMN,又PB⊂平面PBC,
所以平面PBC⊥平面ADMN;
(2)解法一:如图,连结DN,由(1)知PB⊥平面ADMN,
所以,DN为直线BD在平面ADMN内的射影,且DN⊥BN,
所以,∠BDN即为直线BD与平面ADMN所成的角.
在直角梯形ABCD内,过C作CH⊥AD于H,则四边形ABCH为矩形,
CH=AB=3,AH=BC=1,在Rt△CDH中,DH=CHtan∠ADC=33=1,
所以,AD=AH+DH=2,BD=AD2+AB2=7,
而PB=3+3=6,在Rt△BDN中,∠BND=90∘,BN=12PB=62,BD=7,
所以sin∠BDN=BNBD=627=4214,
综上,直线BD与平面ADMN所成角的正弦值为4214.
解法二:在直角梯形ABCD内,过C作CH⊥AD于H,则四边形ABCH为矩形,
CH=AB=3,AH=BC=1,在Rt△CDH中,DH=CHtan∠ADC=33=1,
所以,AD=AH+DH=2,
以A点为原点,AB、AD、AP分别为x、y、z轴,建系如图,
则A0,0,0,D0,2,0,N32,0,32,B3,0,0,P0,0,3.
由(1)知,PB⊥平面ADMN,平面ADMN法向量可取为PB=3,0,-3,BD=-3,2,0,
设直线BD与平面ADMN所成角为θ,则sinθ=PB⋅BDPBBD=3×-3+0×2+-3×03+0+33+4+0=4214,
综上,直线BD与平面ADMN所成角的正弦值为4214.
16.(23-24高二下·广东·期末)如图,在三棱柱ABC-A1B1C1中,侧棱AA1⊥底面ABC,底面△ABC是正三角形,AB=AA1=3,点E、F分别在AB、A1C1上,且AE=13AB,C1F=13A1C1.
(1)求证:A1E//平面BCF;
(2)求直线BB1与平面BCF所成角的余弦值.
【答案】(1)证明见解析
(2)23913⋅
【分析】(1)在线段BC上取一点G,使CG=13BC,连结EG、FG,先证四边形A1FGE为平行四边形,所以A1E∥FG,从而可得A1E//平面BCF;
(2)以B为坐标原点,Bx,BC,BB1所在直线分别为x,y,z轴建立如图空间直角坐标系,利用线面角的空间向量法求解.
【详解】(1)在线段BC上取一点G,使CG=13BC,连结EG、FG,
在△ABC中,因为AE=13AB,CG=13BC,所以BEAB=BGBC=23,
所以EG∥AC且EG=23AC,
因为C1F=13A1C1,A1C1//AC,且A1C1=AC,
所以A1F∥AC,且A1F=23AC,
所以EG∥A1F且EG=A1F,
故四边形A1FGE为平行四边形,所以A1E∥FG,
又A1E⊄平面BCF,FG⊂平面BCF, 所以A1E∥平面BCF.
(2)以B为坐标原点,Bx,BC,BB1所在直线分别为x,y,z轴建立如图空间直角坐标系,
因为底面DABC是正三角形,AB=AA1=3,所以点B0,0,0,点C0,3,0,
点A332,32,0,点B10,0,3,点C10,3,3,
因为C1F=13CA,所以点F32,52,3,
则BC=0,3,0,BF=32,52,3,BB1=0,0,3,
设平面BCF的一个法向量为n=x,y,z.
由n⋅BC=3y=0n⋅BF=32x+52y+3z=0,令z=-3,
得平面BCF的一个法向量为n=6,0,-3,
设直线BB1与平面BCF所成角的大小为θ,
则sinθ=BB1⋅nBB1n=0,0,3⋅6,0,-33×39=1313,
所以csθ=1-sin2θ=1-13132=23913,
所以直线BB1与平面BCF所成角的余弦值为23913⋅
17.(23-24高二下·广东广州·期末)如图,在五棱锥P-ABCDE中,PA⊥平面ABCDE,AE//BC,AB//CD,AC//ED,∠ABC=45∘,AB=22,BC=2AE=4.
(1)求证:平面PCD⊥平面PAC;
(2)已知直线PB与平面PCD所成的角为30∘,求线段PA的长.
【答案】(1)证明见解析
(2)22
【分析】(1)由余弦定理得AC⊥AB,再由线面垂直的判定定理可得答案;
(2)做NE⊥AC交AC于点N,以A为原点,AP,AB,AC所在的直线分别为x,y,z建立空间直角坐标系,设AP=tt>0,求出BP、平面PCD的一个法向量,由线面角的向量求法求出t可得答案,
【详解】(1)∠ABC=45∘,AB=22,BC=4.
由余弦定理得AC2=AB2+BC2-2AB×BCcs45∘
=8+16-2×22×4×22=8,
所以AC2+AB2=BC2,故AC⊥AB,
因为AB//CD,所以AC⊥CD,
因为PA⊥平面ABCDE,CD⊂平面ABCDE,所以PA⊥CD,
因为AC∩PA=A,AC、PA⊂平面PAC,所以CD⊥平面PAC,
因为CD⊂平面PCD,所以平面PCD⊥平面PAC;
(2)做NE⊥AC交AC于点N,所以四边形ENCD是长方形,
因为AE//BC,∠BCA=45∘,所以∠NAE=45∘,
因为AE=2,所以CD=NE=2,
由(1)知,AP,AB,AC互相垂直,以A为原点,
AB,AC,AP所在的直线分别为x,y,z轴建立空间直角坐标系,
设AP=tt>0,则P0,0,t,B22,0,0,C0,22,0,D-2,22,0,
BP=-22,0,t,PC=0,22,-t,PD=-2,22,-t,
设n=x,y,z为平面PCD的一个法向量,
则n⋅PC=0n⋅PD=0,即22y-tz=0-2x+22y-tz=0,令y=2,则z=4t,x=0,
所以n=0,2,4t,
所以sin30∘=csn,BP=n⋅BPn⋅BP=42+16t2×8+t2=12,
解得t=22,所以P0,0,22,A0,0,0,
所以线段PA的长为22.
18.(23-24高二下·广东·期末)如图,四棱锥P-ABCD的侧面PCD为正三角形,底面ABCD为梯形,AB//CD,平面PCD⊥平面ABCD,已知CD=4AB=4,PM=13MD.
(1)证明:AM //平面PBC;
(2)若AC=AD,PA=32,求直线AM与平面PAB所成角的正弦值.
【答案】(1)证明见解析
(2)1326
【分析】(1)取PC上的点N,使PN=14PC,可得MN=AB,则由线线平行可证线面平行;
(2)取CD中点O,连AO,PO,根据题意可证AO⊥CD,PO⊥平面ABCD,所以以O为坐标原点,OA,OC,OP分别为x,y,z轴正方向,建立如图所示空间直角坐标系A-xyz,利用线面角的空间向量法求解.
【详解】(1)取PC上的点N,使PN=14PC,
则MN=PN-PM=14PC-PD=14DC=AB,
所以四边形ABNM为平行四边形,所以AM//BN,
又BN⊂平面PBC,AM⊄平面PBC,所以AM //平面PBC;
(2)取CD中点O,连AO,PO,因为AC=AD,所以AO⊥CD,
因为△PCD为正三角形,所以PO⊥CD,PO=23,
又平面PCD⊥平面ABCD,平面PCD∩平面ABCD=CD,PO⊂平面PCD,
所以PO⊥平面ABCD,
因为AO⊂平面ABCD,所以PO⊥AO,AO=PA2-PO2=6,
以O为坐标原点,OA,OC,OP分别为x,y,z轴正方向,建立如图所示空间直角坐标系A-xyz,
则A(6,0,0),C(0,2,0),D(0,-2,0),B(6,1,0),P(0,0,23),
则AB=(0,1,0),PA=(6,0,-23),AM=AP+14PD=-6,-12,332,
设n=(x,y,z)为平面PAB的法向量,
则n⋅AB=0n⋅PA=0⇒y=06x-23z=0,可取n=2,0,1,
,
故直线AM与平面PAB所成角的正弦值为1326.
19.(23-24高二下·江苏泰州·期末)如图,在四棱锥P-ABCD中,平面PAD⊥平面ABCD,AB⊥AD,AB+AD=5,CD=2,∠PAD=120°,∠ADC=45°.
(1)求证:平面PAB⊥平面PAD;
(2)设AB=AP.
①若直线PB与平面PCD所成角的正弦值为3344,求线段AB的长.
②在线段AD上是否存在点G,使得点P,C,D在以G为球心的球上?若存在,求线段AB的长;若不存在,说明理由.
【答案】(1)证明见解析
(2)①AB=2或AB=7023;②不存在点G,理由见解析
【分析】(1)利用面面垂直的性质可证得AB⊥平面PAD,再利用面面垂直的判定定理即可证得结论;
(2)①依题建系,设AB=t,利用题设条件,分别求得相关点和向量的坐标,利用空间向量坐标的夹角公式列出方程,求解即得t的值;
②假设存在点G,可由GC=GD推得GD=1,得点G坐标,由GP=GD得方程t2-4t+15=0,因此方程无实数解,假设不成立.
【详解】(1)在四棱锥P-ABCD中,平面PAD⊥平面ABCD,AB⊥AD,
AB⊂平面ABCD,平面PAD∩平面ABCD=AD,
所以AB⊥平面PAD,
又AB⊂平面PAB,所以平面PAB⊥平面PAD.
(2)如图以A为原点,以AB所在直线为x轴,以AD所在直线为y轴建立如图所示直角空间坐标系A-xyz,
设AB=t,则AP=t,由AB+AD=5, CD=2,∠PAD=120°,∠ADC=45°,
则Bt,0,0,P0,-t2,3t2,因AD=5-t,则D0,5-t,0,C1,4-t,0,
所以CP=-1,t2-4,3t2,CD=-1,1,0
①设平面PCD的法向量为n=x,y,z,由n⊥CP,n⊥CD,得:
-x+t-82y+3t2z=0-x+y=0,可取n=1,1,10-t3t
设直线PB与平面PCD所成角为θ,
则有:sinθ=csn,BP,BP=-t,-t2,3t2,
即:3344=-t-t2+10-t21+1+10-t3t2t2+t24+3t24,化简得:23t2-116t+140=0,
解得t=2或t=7023,即AB=2或AB=7023.
②如图,假设在线段AD上是否存在点G,使得点P,C,D在以G为球心的球上,
由GC=GD,得∠GCD=∠GDC=45°,所以∠CGD=90°,
所以GD=CDcs45°=1,
又AB=t得AD=5-t,AG=AD-GD=4-t,所以G0,4-t,0,P0,-t2,3t2
由GP=GD得-t2-4-t2+3t22=1,即t2-42+34t2=1,
亦即t2-4t+15=0(*),
因为Δ=-42-4×15<0,所以方程(*)无实数解,
所以线段AD上不存在点G,使得点P,C,D在以G为球心的球上.
【点睛】方法点睛:本题主要考查利用空间向量解决线面所成角以及多点是否在同一球面上的开放性问题,属于较难题.
根据题意,创建合适的空间直角坐标系,利用空间向量夹角的坐标表达式即可求解相关问题,对于开放性问题,一般是假设结论成立,通过推理计算求得结论成立的条件或者推导出矛盾.
课程标准
学习目标
1.掌握求线面角的两种基本方法,即空间向量法与几何法
2.灵活运用两种基本方法求线面角
1.理解直线与平面的夹角的概念。
2.学习如何计算直线与平面的夹角。
3.掌握求直线与平面夹角的方法。
4.能够应用所学知识解决相关的题目。
数学2.1 坐标法当堂检测题: 这是一份数学<a href="/sx/tb_c4002057_t7/?tag_id=28" target="_blank">2.1 坐标法当堂检测题</a>,共14页。
人教B版 (2019)选择性必修 第一册第二章 平面解析几何2.2 直线及其方程2.2.2 直线的方程随堂练习题: 这是一份人教B版 (2019)选择性必修 第一册<a href="/sx/tb_c4002060_t7/?tag_id=28" target="_blank">第二章 平面解析几何2.2 直线及其方程2.2.2 直线的方程随堂练习题</a>,共57页。试卷主要包含了经过点P称为直线的点斜式方程等内容,欢迎下载使用。
高中数学人教B版 (2019)选择性必修 第一册2.2.3 两条直线的位置关系巩固练习: 这是一份高中数学人教B版 (2019)选择性必修 第一册<a href="/sx/tb_c4002061_t7/?tag_id=28" target="_blank">2.2.3 两条直线的位置关系巩固练习</a>,共34页。试卷主要包含了若直线l1,设直线l1等内容,欢迎下载使用。













