

高中1.1.3 空间向量的坐标与空间直角坐标系一课一练
展开知识点01 正交基底与单位正交基底
【即学即练1】(22-23高二上·山东烟台·阶段练习)设{i,j,k}是单位正交基底,已知a=i+j,b=j+k,c=k+i,若向量p在基底{a,b,c}下的坐标为(8,6,4),则向量p在基底{i,j,k}下的坐标是( )
A.(10,12,14)B.(14,12,10)
C.(12,14,10)D.(4,3,2)
【即学即练2】(20-21高二·江苏·课后作业)已知i,j,k为一个单位正交基底,试写出下列向量的坐标:
(1)a=-2i+8j+3k;
(2)b=-5i+2k.
知识点02 空间直角坐标系
1.定义:如图,在空间选定一点0和一个单位正交基底{i,j,k}以0为原点,分别以i,j,k的方向为正方向建立三条数轴:x轴、y轴、z轴,它们都叫作坐标轴,这是我们说建立了一个空间直角坐标系O-xyz。
其中点O叫作坐标原点,x轴、y轴、z轴叫作坐标轴,三条坐标轴中的每两条确定一个坐标平面,分别叫作xy平面、yz平面和xz平面。
2.右手直角坐标系
在空间直角坐标系中,让右手拇指指向x轴的正方向,食指指向y轴的正方向,若中指指向z轴的正方向,则称这个坐标系为右手直角坐标系。
【即学即练3】(23-24高二上·上海·期中)如图所示,以长方体ABCD-A1B1C1D1的顶点D为坐标原点,过D的三条棱所在的直线为坐标轴,建立空间直角坐标系,若DB1的坐标为3,4,2,则AC1的坐标为 .
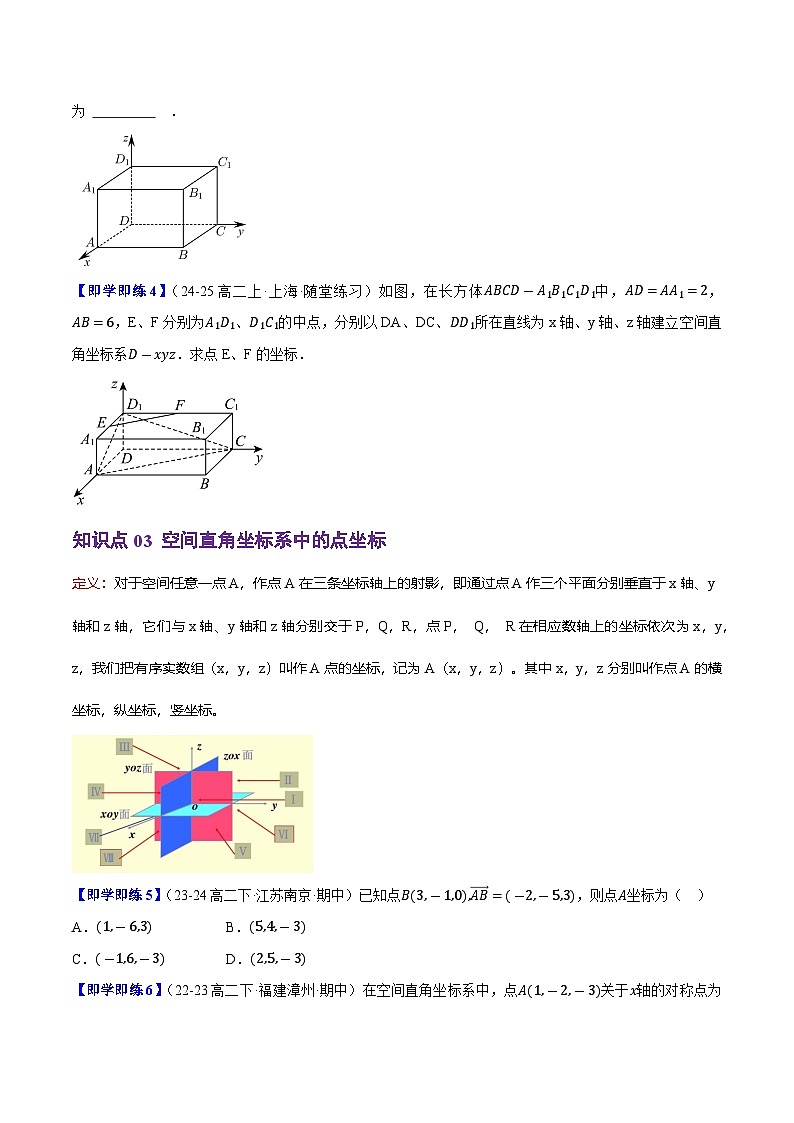
【即学即练4】(24-25高二上·上海·随堂练习)如图,在长方体ABCD-A1B1C1D1中,AD=AA1=2,AB=6,E、F分别为A1D1、D1C1的中点,分别以DA、DC、DD1所在直线为x轴、y轴、z轴建立空间直角坐标系D-xyz.求点E、F的坐标.
知识点03 空间直角坐标系中的点坐标
定义:对于空间任意一点A,作点A在三条坐标轴上的射影,即通过点A作三个平面分别垂直于x轴、y轴和z轴,它们与x轴、y轴和z轴分别交于P,Q,R,点P, Q, R在相应数轴上的坐标依次为x,y,z,我们把有序实数组(x,y,z)叫作A点的坐标,记为A(x,y,z)。其中x,y,z分别叫作点A的横坐标,纵坐标,竖坐标。
【即学即练5】(23-24高二下·江苏南京·期中)已知点B3,-1,0,AB=-2,-5,3,则点A坐标为( )
A.1,-6,3B.5,4,-3
C.-1,6,-3D.2,5,-3
【即学即练6】(22-23高二下·福建漳州·期中)在空间直角坐标系中,点A(1,-2,-3)关于x轴的对称点为( )
A.(-1,2,3)B.(1,2,-3)C.(1,2,3)D.(-1,-2,-3)
知识点04 空间向量的坐标运算
1.空间向量的坐标运算
(1)设a=(x1,y1,z1),b=(x2,y2,z2),则
①a+b=(x1+x2,y1+y2,z1+z2)
②a-b=(x1-x2,y1-y2,z1-z2)
③λa=(λx1,λy1,λz1)(a∈R).
= 4 \* GB3 \* MERGEFORMAT ④若u,v是两个实数,ua+vb=(ux1+vx2,uy1+vy2,uz1+vz2);
= 5 \* GB3 \* MERGEFORMAT ⑤a·b=x1x2+y1y2+z1z2;
= 6 \* GB3 \* MERGEFORMAT ⑥|a|=eq \r(a·a)=eq \r(x\\al(2,1)+y\\al(2,1)+z\\al(2,1));
= 7 \* GB3 \* MERGEFORMAT ⑦当a≠0且b≠0时,cs〈a,b〉=eq \f(a·b,|a|·|b|)=eq \f(x1x2+y1y2+z1z2,\r(x\\al(2,1)+y\\al(2,1)+z\\al(2,1))\r(x\\al(2,2)+y\\al(2,2)+z\\al(2,2))).
(2)设A(x1,y1,z1),B(x2,y2,z2),则AB=OB-OA=(x2-x1,y2-y1,z2-z1).即一个向量的
坐标等于表示这个向量的有向线段的终点坐标减去起点坐标.
2.空间向量平行、垂直的坐标表示
(1)已知空间向量a=(x1,y1,z1),b=(x2,y2,z2),且a≠0,则a//b⟺b=λa⟺x2=λx1,y2=λy1,z2=λz1(λ∈R).
(2)a⊥b⇔a·b=0⇔x1x2+y1y2+z1z2=0.
3.空间向量坐标的应用
(1)点P(x,y,z)到坐标原点O(0,0,0)的距离OP=eq \r(x2+y2+z2).
(2)任意两点P1(x1,y1,z1),P2(x2,y2,z2)间的距离P1P2=eq \r(x2-x12+y2-y12+z2-z12).
【即学即练7】(23-24高一下·天津·阶段练习)已知A2,-4,-1,B=-1,5,1,C3,-4,1,令a=CA,b=CB,则a+b对应的坐标为( )
A.5,-9,2B.-5,9,-2C.5,9,-2D.5,-9,-2
【即学即练8】(23-24高二下·甘肃酒泉·期末)已知向量a=1,0,3,b=0,-1,2,c=3,1,0则a⋅b-c=( )
A.-3B.3C.9D.0
难点:空间向量与动点问题
示例1:(多选)(23-24高二下·福建漳州·阶段练习)如图,在棱长为1的正方体ABCD-A1B1C1D1中,M为B1C1边的中点,点P在底面ABCD内运动(包括边界),则下列说法正确的有( ).
A.不存在点P,使得D1P⊥AD1
B.过三点A,M,D1的正方体ABCD-A1B1C1D1的截面面积为98
C.若D1P⊥B1D,则P点在正方形ABCD内运动轨迹长为22
D.点N在棱BB1上,且B1N=4NB,若D1P⊥NP,则点P的轨迹是圆
【题型1:空间向量的坐标表示】
例1.(23-24高二上·湖北·期末)已知点A2,0,1,B0,2,0,C0,0,3,D1,1,0,E0,0,a,直线DE平行△ABC所在的平面,则a=( )
A.12B.32C.2D.52
变式1.(23-24高二上·湖北武汉·期中)在空间直角坐标系中,已知点A(1,3,-4)关于原点中心对称的点为B,而点B关于x轴对称的点为C,则AC=( )
A.(-2,0,0)B.(-2,3,0)C.(-2,0,-4)D.(1,0,-4)
变式2.(23-24高二上·重庆九龙坡·期中)若M1,0,2,N2,m+1,3,P2,2,n+1三点共线,则m+n=( )
A.4B.-2C.1D.3
变式3.(23-24高二上·四川成都·阶段练习)如图,在长方体ABCD-A1B1C1D1中,AB=5,AD=4,AA1=3,以直线DA,DC,DD1分别为x轴,y轴,z轴,建立空间直角坐标系Dxyz,则下列结论中不正确的是( )
A.点A关于直线DD1对称的点为(-4,0,0)B.点C1关于点B对称的点为(8,5,-3)
C.点B1的坐标为(3,5,4)D.点C关于平面ABB1A1对称的点为(8,5,0)
变式4.(23-24高二上·山西运城·阶段练习)已知正方体ABCD-A'B'C'D'的棱长为1,以D为原点,DA,DC,DD'所在直线分别为x轴,y轴,z轴,建立空间直角坐标系,则以下坐标表示的点在平面A'BC'内的是( )
A.23,23,13B.34,34,12C.12,12,12D.-1,32,1
变式5.(23-24高二上·福建厦门·阶段练习)设a1=2m-j+k,a2=m+3j-2k,a3=-2m+j-3k,a4=3m+2j+5k,其中m,j,k是两两垂直的单位向量,若a4=λa1+μa2+va3,则实数λ,μ,v的值分别是( )
A.1,-2,3B.-2,1,-3
C.-2,1,3D.-1,2,3
变式6.(23-24高三上·安徽·阶段练习)已知空间向量a=-3,2,m,b=-1,-1,3,c=1,-4,n,若a,b,c共面,则m+n= .
变式7.(23-24高二上·河北石家庄·期中)在空间直角坐标系中,若平行四边形ABCD的顶点A0,-2,1,B2,-3,0,C2,0,1,则顶点D的坐标为 .
变式8.(23-24高二上·山东聊城·阶段练习)已知直线l经过A-2,1,1,B1,0,-3两点,直线l上一点P,使得AP=-AB,则点P坐标 .
【题型2:空间向量的加减数乘与数量积】
例2.(23-24高二上·广东惠州·阶段练习)如图所示,在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD为正方形,M为AB的中点,N为PD的中点.若PA=4,AB=2,则MN⋅PC= .
变式1.(24-25高二上·上海·课堂例题)已知O为原点,OA=1,2,3,OB=2,1,2,OP=1,1,2,点Q在直线OP上运动,则QA⋅QB取得最小值时,点Q的坐标为( )
A.12,34,13B.12,23,13C.43,43,83D.43,43,73
变式2.(23-24高二上·福建泉州·期末)四棱锥P-ABCD的底面为矩形,PC⊥平面ABCD,M在棱PC上,AD=2,则AM⋅BC=( )
A.-4B.4C.-32D.32
变式3.(23-24高二上·河北沧州·阶段练习)《九章算术》是我国东汉初年编订的一部数学经典著作,在第五卷《商功》中记载“斜解立方,得两堑堵”,堑堵是底面为直角三角形的直三棱柱.已知在堑堵ABC-A1B1C1中,AB⊥AC,AB=2,AC=AA1=3,BE=EA1,CF=2FA1,则AE⋅BF=( )
A.-1B.1C.-3D.12
变式4.(多选)(23-24高二上·河北石家庄·期末)如图,长方体ABCD-A1B1C1D1中,CC1=C1D1=2,C1B1=1,点P为线段B1C上一点,则C1P⋅D1P的值可以为( )
A.13B.45C.23D.2
变式5.(23-24高二下·上海青浦·期末)在空间直角坐标系中,点A(2,-1,3)关于平面xOz的对称点为B,则OA⋅OB= .
变式6.(23-24高二下·云南曲靖·阶段练习)已知空间向量a=1,0,2,b=-2,1,3,则a-2b= .
变式7.(23-24高二下·上海·期中)已知a=-1,2,0,b=2,0,1,则2a+3b⋅a-b= .
变式8.(23-24高二上·四川泸州·期末)已知向量a=1,1,x,b=1,1,2,c=1,-1,1,若a+c⋅b=-1,则实数x= .
【方法技巧与总结】
关于空间向量坐标运算的两类问题
(1)直接计算问题
首先将空间向量用坐标表示出来,然后准确运用空间向量坐标运算公式计算.
(2)由条件求向量或点的坐标
首先把向量用坐标形式设出来,然后通过建立方程(组),解方程(组)求出其坐标..
【题型3:空间向量的模长】
例3.(23-24高二下·上海·期中)已知AB=0,1,2,则AB= .
变式1.(2024高三·全国·专题练习)在空间直角坐标系O-xyz中,已知点A1,0,2,B0,2,1,点C,D分别在x轴,y轴上,且AD⊥BC,那么CD的最小值是( )
A.55B.255C.22D.2
变式2.(23-24高二上·广东惠州·阶段练习)在空间直角坐标系中,A(-1,2,0),点B(-1,1,2)关于y轴的对称点为C,则|AC|=( )
A.5B.11C.3D.10
变式3.(23-24高二上·浙江杭州·期中)如图,在边长为3的正方体ABCD-A1B1C1D1中,BC=3EC,点P在底面正方形ABCD上移动(包含边界),且满足B1P⊥D1E,则线段B1P的长度的最大值为( )
A.319010B.22C.32D.1663
变式4.(23-24高二上·湖北武汉·期中)如图所示,三棱锥A-BCD中,AB⊥平面BCD,∠BCD=π2,BC=2AB=2CD=2,点P为棱AC的中点,E,F分别为直线DP,AB上的动点,则线段EF的最小值为( )
A.24B.22C.104D.52
变式5.(23-24高二下·贵州六盘水·期中)已知a=2,1,0,b=-1,0,1.则a+b= .
变式6.(23-24高二上·上海·期末)在空间直角坐标系中,点P坐标可记为x,y,z:定义柱面坐标系,在柱面坐标系中,点P坐标可记为r,θ,z.如图所示,空间直角坐标x,y,z与柱面坐标r,θ,z之间的变换公式为:x=rcsθ,y=rsinθ,z=z.则在柱面坐标系中,点A1,π2,2与点B2,θ,-1两点距离的最小值为 .
变式7.(23-24高二上·浙江绍兴·期中)已知向量a=(0,-1,1),b=(4,1,0),|λa+b|=29,则λ= .
变式8.(24-25高二上·上海·课堂例题)如图,正方体ABCD-A1B1C1D1的棱长为1,动点M在线段CC1上,动点P在平面A1B1C1D1上,且AP⊥平面MBD1.
(1)当点M与点C重合时,求线段AP的长度;
(2)求线段AP长度的最小值.
【题型4:空间向量的夹角】
例4.(23-24高一下·北京顺义·阶段练习)已知向量a=1,2,2,b=-2,1,-1.
(1)求a⋅b;
(2)求2a-b;
(3)求csa,b.
变式1.(23-24高二上·河南鹤壁·阶段练习)已知{i→,j→,k→}是空间的一个单位正交基底,且AB→=-i→+j→-k→,CD→=2i→+j→+k→,则AB与CD夹角的余弦值为( )
A.12B.-13C.33D.-23
变式2.(23-24高二上·辽宁·阶段练习)如图,在正方形中,点E,F分别是线段AD,BC上的动点,且AE=BF,AC与EF交于G,EF在AB与CD之间滑动,但与AB和CD均不重合.现将四边形EFCD沿直线EF折起,使平面EFCD⊥平面ABFE,在EF从AB滑动到CD的过程中,∠AGC的大小( )
A.先变小后变大B.先变大后变小C.不发生变化D.由小变大
变式3.(多选)(23-24高二上·陕西咸阳·阶段练习)如图,在直三棱柱ABC-A1B1C1中,CA=CB=1,∠BCA=90∘,棱AA1=2,M,N分别是A1B1,A1A的中点,则( )
A.BN=3B.BA1⋅MC1=0C.VB-C1MN=32D.csBA1,CB1=3010
变式4.(多选)(23-24高二上·福建泉州·期中)在菱形纸片ABCD中,E,F分别为AD,BC的中点,O是菱形ABCD的中心,AB=2,∠ABC=2π3,将菱形纸片ABCD沿对角线AC折成直二面角,以O为原点,OB,OC,OD所在的直线分别为x轴、y轴、z轴,建立如图所示的空间直角坐标系,则( )
A.E0,-32,12B.F32,12,0
C.EF=12,3,-12D.cs∠EOF=-34
变式5.(24-25高二上·上海·随堂练习)若a=-1,λ,-2,b=2,-2,-1,a与b的夹角为π3,则λ的值为 .
变式6.(2024高二上·全国·专题练习)已知向量a=3,0,1,b=k,2,0,若a与b夹角为π3,则k的值为 .
变式7.(23-24高二上·江苏盐城·期末)已知OA=1,0,0,OB=1,1,0, OC=1,1,1,点M在直线OC上运动,则csOA,MB的最大值为 .
【题型5:空间向量的投影】
例5.(23-24高二下·江苏淮安·阶段练习)已知向量a=(9,8,5),b=(2,1,1),则向量a在向量b上的投影向量c=( )
A.313,-316,-316B.-313,316,316
C.313,316,316D.-313,-316,-316
变式1.(23-24高二上·云南昭通·期末)已知空间向量a=(2,1,-3),则向量a在坐标平面xOz上的投影向量是( )
A.(0,2,1)B.(2,1,0)
C.(0,1,-3)D.(2,0,-3)
变式2.(23-24高二上·重庆九龙坡·期末)已知向量a=1,1,2,b=-3,2,0,则a+b在a上的投影向量为( )
A.32,32,322B.1510,1510,3010
C.34,34,324D.-25,35,25
变式3.(23-24高三上·江苏苏州·阶段练习)如图,圆台OO1的轴截面为等腰梯形ABCD,AB=2CD,E在上底面的圆周上,且∠CO1E=45∘,则AE在AB上的投影向量为( )
A.3+28ABB.4+28AB
C.3+38ABD.4+38AB
变式4.(多选)(23-24高二上·江苏盐城·期末)在空间直角坐标系O-xyz中,已知点A2,0,0,B1,1,-2,C2,3,1,则( )
A.AC=23
B.异面直线OB与AC所成角的余弦值为1530
C.AB⋅BC=-5
D.OB在BC上的投影向量的模为31111
变式5.(24-25高二上·上海·随堂练习)已知向量a=2,-3,0,b=0,3,4,则向量a在向量b方向上的投影向量为 .
变式6.(23-24高二上·福建莆田·阶段练习)已知向量a在向量b上的投影向量是-32b,且b=1,1,-1,则a⋅b= .
变式7.(23-24高二上·吉林长春·阶段练习)如图,已知正方体ABCD-A1B1C1D1的棱长为1,E为棱B1C1上的动点,则AE在AC方向上的投影向量的模的取值范围为 .
【题型6:空间向量的平行、垂直与锐角、钝角问题】
例6.(23-24高二下·江苏连云港·期中)设x,y∈R,向量 a=x,1,1,b=1,-1,y,c=2,-2,2,且a⊥c,b//c,则x+y的值为( )
A.-1B.1C.2D.3
变式1.(23-24高二上·浙江湖州·期末)已知向量a=k,1,2,b=k,0,-2,则“k=2”是“a⊥b”的( )
A.充分不必要条件B.必要不充分条件C.充分必要条件D.既不充分也不必要条件
变式2.(24-25高二上·上海·课堂例题)已知空间向量a=1,2,-2、b=3,λ,μ-1,若a//b,则λ+μ= .
变式3.(23-24高二下·湖北·开学考试)已知a=m+1,1,-1,b=1,n,3,其中m>0,n>0,若a⊥b,则1m+4n的最小值为 .
变式4.(23-24高二上·辽宁大连·期末)若空间向量a=1,1,x,b=2,x,4,向量a、b夹角为锐角,则x的取值范围是
变式5.(22-23高二下·江苏·课后作业)若a=2,-1,4,b=-1,t,-2,若a与b的夹角是钝角,则t的值的取值范围为 .
变式6.(23-24高二下·甘肃兰州·期中)已知空间中三点A2,0,-2,B1,-1,-2,C3,0,-4,设a=AB,b=AC.
(1)已知a+kb⊥b,求k的值;
(2)若c=6,且c∥BC,求c的坐标.
变式7.(22-23高二上·黑龙江牡丹江·阶段练习)已知a→=x,1,1,b→=1,y,1,c→=2,-4,2,x,y∈R,且a⊥b,b∥c.
(1)求a+b;
(2)求向量a+b与2a+b-c夹角的大小.
变式8.(23-24高二上·广西河池·阶段练习)已知a=x,1,0,b=-1,y,2,c=2,-2,1,b=5,a⊥c,
(1)若a+kb、2a+b共线,求实数k;
(2)若向量a+kb与2a+b所成角为锐角,求实数k的范围.
【题型7:最值与取值范围问题】
例7.(23-24高二上·广东湛江·阶段练习)已知直线l和平面α,且l∥α,l的方向向量为l=2,m,1,平面α的一个法向量为n=-1,1,n,m>0,n>0,则1m+1n的最小值为( )
A.2B.4C.42D.22
变式1.(23-24高二上·广东惠州·阶段练习)如图,在四棱锥D1-ABCD中,D1D⊥平面ABCD,四边形ABCD是正方形,且D1D=DA=DC=3,E,F分别为D1B的三等分点,若P为底面ABCD上的一个动点,则PE+PF的最小值为( )
A.11B.522C.1+6D.33
变式2.(多选)(23-24高二上·浙江·期中)已知向量e1=t,2t,2,e2=2t-2,-t,-1,则下列结论正确的是( )
A.若e1⊥e2,则t=-1B.若e1 ∥ e2,则t=45
C.e1的最大值2D.e1的最小值2
变式3.(23-24高二下·江苏扬州·阶段练习)已知点O0,0,0,A1,2,2,B2,1,1,P1,0,2,点Q在直线OP上运动,当QA⋅QB取得最小值时,点Q的坐标是 .
变式4.(23-24高三上·湖南长沙·阶段练习)在棱长为3的正方体ABCD-A1B1C1D1中,点E满足A1E=2EB1,点F在平面BC1D内,则|A1F+|EF|的最小值为 .
变式5.(23-24高二上·河北衡水·阶段练习)如图,在四棱锥S-ABCD中,底面ABCD为正方形,AB=2,SD⊥底面ABCD,点E、F分别为SC、AB的中点,若线段SD上存在点G,使得GE⊥GF,则线段SD的长度最小值为 .
变式6.(23-24高二下·上海·阶段练习)在空间直角坐标系O-xyz中,有两点A(0,-2,4),B(2,1,5),P是xOy平面上任意一点,则AP+BP的最小值为 .
变式7.(23-24高二下·江苏宿迁·期中)已知A(1,-2,1),向量a=(-3,4,12),且满足AB=2a
(1)求点B的坐标;
(2)若点M在直线OA(O为坐标原点)上运动,当MA⋅MB取最小值时,求点M的坐标.
一、单选题
1.(河南省开封市2023-2024学年高二下学期7月期末数学试题)已知a=2,-1,3,b=4,2,x,且a⊥b,则x=( )
A.-6B.-2C.2D.6
2.(23-24高一下·湖南·期末)已知A-2,1,3,B1,-1,4,则AB=( )
A.3,0,1B.-1,-2,1C.-1,0,7D.3,-2,1
3.(23-24高二下·甘肃兰州·期中)空间直角坐标系中,点P1,2,3关于平面xOy的对称点是( )
A.-1,-2,3B.-1,2,3C.1,-2,3D.1,2,-3
4.(23-24高一下·天津·阶段练习)已知向量:a=-3,2,5,b=1,5,-1,则a-2b=( )
A.-4,-3,4B.-5,-8,7
C.-5,-8,3D.-1,-3,6
5.(23-24高二下·山东烟台·阶段练习)已知向量a=0,0,1,b=1,-1,1,向量a+b在向量a上的投影向量为( ).
A.0,0,2B.0,0,1
C.0,0,-1D.0,0,-2
6.(23-24高二上·河南省直辖县级单位·阶段练习)已知空间三点A1,1,1,B-1,0,4,C2,-2,3,则AB与CA的夹角为( )
A.π3B.π6C.2π3D.5π3
7.(23-24高二下·福建莆田·期末)已知向量AB=(1,m,-3),AC=(-3,6,9),若A,B,C三点共线,则m=( )
A.-3B.-2C.2D.3
8.(23-24高二下·福建漳州·期末)已知向量a=(1,0,2),b=(-2,1,-2),c=(0,1,λ),若a,b,c三个向量共面,则实数λ=( )
A.1B.2C.3D.4
二、多选题
9.(23-24高二上·四川宜宾·期末)已知向量a=2x,1,1,b=1,-y,2,则( )
A.若x=14,y=-2,则a//b
B.若x=1,y=1,则a⊥b
C.若x=12,y=1,则csa,b=23
D.若x=12,y=1,则向量a在向量b上的投影向量c=13,-13,23
10.(23-24高二上·重庆·期末)给出下列命题,其中正确的是( )
A.任意向量a,b,c满足(a⋅b)⋅c=a⋅(b⋅c)
B.在空间直角坐标系中,点P(-1,3,5)关于坐标平面yOz的对称点是N(1,3,5)
C.已知a=e1-2e2+e3,b=-e1+3e2+2e3,c=-3e1+7e2,e1,e2,e3为空间向量的一个基底,则向量a,b,c能共面
D.已知A(-1,1,2),B(2,2,4),C(3,-2,0),则向量AC在向量AB上的投影向量是1114(3,1,2)
11.(23-24高二上·广东揭阳·阶段练习)下面四个结论正确的是( )
A.向量a,b(a≠0,b≠0),若a⊥b,则a⋅b=0
B.若空间四个点P,A,B,C,PC=14PA+34PB,则A,B,C三点共线
C.已知{a,b,c}是空间的一组基底,若m=a+c,则{a,b,m}也是空间的一组基底
D.已知向量a=(1,1,x),b=(-3,x,9),若x<310,则〈a,b〉为钝角
三、填空题
12.(23-24高二上·四川宜宾·期末)已知A(1,1,0),B(0,4,0),C(2,2,2),则向量AB在AC上的投影向量的坐标是 .
13.(22-23高二上·北京·阶段练习)若异面直线l1,l2的方向向量分别是a=0,-2,-1,b=2,0,4,则异面直线l1与l2的夹角的余弦值等于 .
14.(22-23高二上·北京丰台·阶段练习)已知空间向量a=1,0,2,b=-2,1,3,则a-b= ,a+b⋅a-2b= .
四、解答题
15.(23-24高二下·江苏常州·期中)已知空间三点A-2,0,2,B-1,1,2,C-3,0,4,设a=AB,b=AC.
(1)若ka+b与ka-2b互相垂直,求实数k的值;
(2)若c=3,c//BC,求c.
16.(23-24高二下·江苏南京·阶段练习)已知空间中三点A2,0,-2,B1,-1,-2,C3,0,-4,设a=AB,b=AC.
(1)若c=6,且c∥BC,求向量c;
(2)已知向量ka-b与b互相垂直,求k的值;
(3)若点P1,-1,m在平面ABC上,求m的值.
17.(23-24高二上·广西玉林·阶段练习)已知a=x,4,1,b=-2,y,-1,c=3,-2,z,a∥b,b⊥c.
(1)求实数x,y,z的值;
(2)求a+c与b+c夹角的余弦值.
18.(22-23高二上·广东佛山·阶段练习)如图,在空间直角坐标系O-xyz中,正方体ABCD-A1B1C1D1的棱长为1,顶点A位于坐标原点,若E是棱B1C1的中点,F是侧面CDD1C1的中心.
(1)求点E,F的坐标及EF;
(2)求向量EF在DC1→方向上的投影向量.
19.(21-22高二·全国·课后作业)如图所示,在四棱锥P-ABCD中,△PBC为等腰直角三角形,且∠CPB=90°,四边形ABCD为直角梯形,满足AD//BC,CD⊥AD,BC=CD=2AD=4,PD=26.
(1)若点F为DC的中点,求cs〈AP,BF〉;
(2)若点E为PB的中点,点M为AB上一点,当EM⊥BF时,求|AM||AB|的值.
课程标准
学习目标
1.了解空间向量坐标的定义.
2.掌握空间向量的坐标运算,会计算向量的长度及两向量的夹角.
3.会利用向量的坐标关系,判定两个向量平行或垂直.
4.了解空间直角坐标系,会用空间直角坐标系刻画点的位置.
5掌握空间直角坐标系中两点之间的距离公式和中点坐标公式
1.掌握空间向量的线性运算的坐标表示:掌握空间向量数量积的坐标表示
2.掌握空间向量的模、夹角
3.掌握空间向量坐标与空间向量平行与垂直的关系
正交基底
如果空间一个基底的三个基向量两两互相垂直,那么这个基底叫作正交基底
单位正交基底
当一个正交基底的三个基向量都是单位向量时,称这个基底为单位正交基底,通常用{i,j,k}表示
数学选择性必修 第一册1.1.1 空间向量及其运算同步测试题: 这是一份数学选择性必修 第一册<a href="/sx/tb_c4002044_t7/?tag_id=28" target="_blank">1.1.1 空间向量及其运算同步测试题</a>,共29页。试卷主要包含了定义,表示方法,相反向量,平行向量等内容,欢迎下载使用。
高中数学人教B版 (2019)选择性必修 第一册1.1.3 空间向量的坐标与空间直角坐标系测试题: 这是一份高中数学人教B版 (2019)选择性必修 第一册<a href="/sx/tb_c4002046_t7/?tag_id=28" target="_blank">1.1.3 空间向量的坐标与空间直角坐标系测试题</a>,共52页。
数学2.1 坐标法当堂检测题: 这是一份数学<a href="/sx/tb_c4002057_t7/?tag_id=28" target="_blank">2.1 坐标法当堂检测题</a>,共14页。













