陕西省延安市富县2023-2024学年八年级上学期期中考试数学试卷(含答案)

这是一份陕西省延安市富县2023-2024学年八年级上学期期中考试数学试卷(含答案)，共12页。试卷主要包含了本试卷共8页，满分120分；等内容，欢迎下载使用。
八年级数学试题（卷）（人教版）
老师真诚地提醒你：
1．本试卷共8页，满分120分；
2．答卷前请将密封线内的项目填写清楚；
3．书写要认真、工整、规范；卷面干净、整洁、美观
第一部分（选择题共24分）
一、选择题（共8小题，每小题3分，计24分．每小题只有一个选项是符合题意的，请将正确答案的序号填在题前的答题栏中）
1．甲骨文是我国目前发现最早的文字，其图画性强的特点非常明显，下列甲骨文图画是轴对称的是（ ）
A． B． C． D．
2．从边形的一个顶点出发，可以作条对角线，则的值是（ ）
A．12B．10C．9D．8
3．下列长度的三条线段能组成三角形的是（ ）
A．2，3，6B．5，8，13C．4，4，7D．3，4，8
4．如图，平分，于点，点是射线上的一个动点，若，则的最小值为（ ）
A．4.5B．3.5C．4D．5
5．在平面直角坐标系中，点和关于轴对称，则的值为（ ）
A．B．3C．D．2
6．如图，在中，，点在上，且点与点关于直线对称，则的度数为（ ）
A．B．C．D．
7．如图，AB平分∠CAD，E为AB上一点，若AC=AD，则下列结论错误的是 （ ）
A．BC=BD;B．CE=DE;C．BA平分∠CBD;D．图中有两对全等三角形
8．如图，在中，的垂直平分线相交于点，若，则的度数是（ ）
A．B．C．D．
第二部分（非选择题共96分）
二、填空题（共5小题，每小题3分，计15分）
9．如图，学校门口设置的移动拒马都用钢管焊接成三角形，这样做的数学原理是 ．
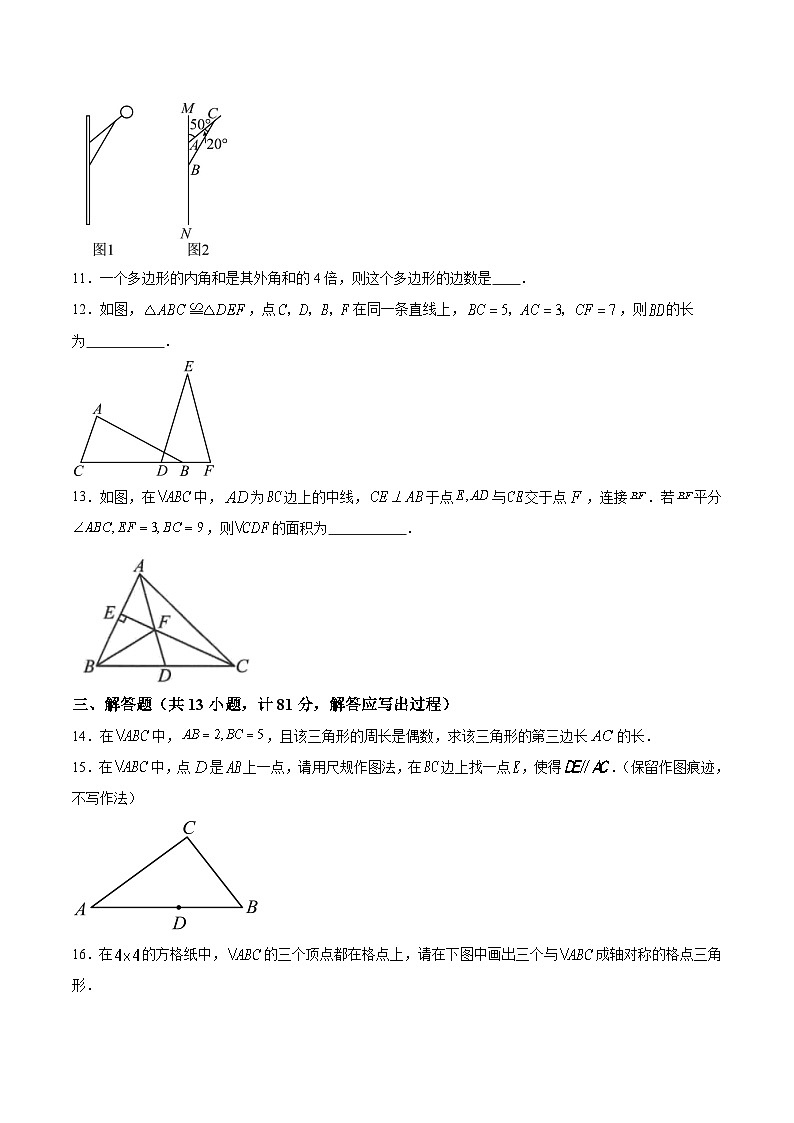
10．图1是一路灯的实物图，图2是该路灯的平面示意图，已知，则图2中的度数为 ．

11．一个多边形的内角和是其外角和的4倍，则这个多边形的边数是 ．
12．如图，，点在同一条直线上，，则的长为 ．
13．如图，在中，为边上的中线，于点与交于点，连接．若平分，则的面积为 ．
三、解答题（共13小题，计81分，解答应写出过程）
14．在中，，且该三角形的周长是偶数，求该三角形的第三边长的长．
15．在中，点是上一点，请用尺规作图法，在边上找一点，使得．（保留作图痕迹，不写作法）
16．在的方格纸中，的三个顶点都在格点上，请在下图中画出三个与成轴对称的格点三角形．

17．如图，在中，点在边上，．求证：．
18．如图，在边长为1的正方形组成的网格中，的顶点均在格点上．
(1)画出关于轴对称的图形；
(2)写出的坐标．
19．在中，垂直平分，点在的延长线上，且满足，求证：点在线段垂直平分线上．

20．如图是一个三角形支架，要检查底角大小是否相等，由于条件限制，无法直接测量．乐乐所在的数学兴趣小组的同学们采用以下方法进行测量：在上量得，在上量得为的三等分点，同时量得和的周长相等，然后他们得出底角相等的结论，这种说法正确吗？为什么？
21．如图，在中，，，是边上的高，是的平分线，求的度数．
22．如图，在中，为延长线上一点，连接分别交于点，且，求的度数．
23．如图，已知点在的内部，且点与点关于对称，交于点，点与点关于对称，交于点分别交于点．
(1)连接，若，求的周长；
(2)若，求证：平分．
24．如图，点分别是正五边形的边上的点，连接交于点，且．
(1)与全等吗？为什么？
(2)求的度数．
25．如图，在中，平分．
(1)求的度数；
(2)求与之间的数量关系．
26．如图，在等腰中，，点为的中点，若点在线段上以每秒2个单位长度的速度由点向点运动，同时，点在线段上以每秒个单位长度的速度由点向点运动，设运动时间为（秒）．
(1)若，经过1秒后，与是否全等？请说明理由；
(2)若，求点的运动速度为多少时，能够使与全等？
答案与解析
1．D
2．C
3．C
4．A
5．A
6．B
7．D
8．C
9．三角形具有稳定性
10．##度
11．10
12．1
13．
14．
15．
如图，点即为所作．
16．
解：如图所示，、、即为所求．

17．
证明：∵，
∴，
在和中，
，
∴，
∴．
18．(1)见解析
(2)
（1）解：即为所作；
（2）根据图象得：，
故答案为：．
19．
证明：垂直平分，
，，
又，
．
又，
，
点在线段的垂直平分线上．
20．
解：做法正确．理由如下：
由题意，得，
∴．
在和中，
，
∴，
∴．
21．
解析：∵在中，，，
∴．
∵是的平分线，
∴，
∵是边上的高，
∴．
∴在中， ，
∴．
22．
解：∵为延长线上一点，
∴，
在和中，
，
∴，
∴，
∵，
∴，
∴．
23．(1)
(2)见解析
解析：（1）∵点P与点M关于对称，
∴．
同理：．
∴的周长；
（2）∵，Q、R为，的中点，
∴，，
∴．
又∵点与点关于对称，点与点关于对称，
∴，
∴平分．
24．(1)见解析
(2)
解析：（1），理由为：
∵五边形是正五边形，
∴．
在与中，
，
∴．
（2）∵，
∴．
∵，
∴，
∴，
∴．
25．(1)
(2)
（1）解：∵平分，
∴，
∴，
（2）解：∵是的外角，
∴，
∴，
∴．
26．(1)与全等，理由见解析
(2)
（1）解：与全等，理由如下：
当时，经过1秒后，
∵，点为的中点，
∴，
∴，
∵，
∴，
∴；
（2）解：当时，则，
∴，
∵，
∴，不符合题意；
当时，则，
∴，
∴，
综上所述，点的运动速度为时，能够使与全等．