数学浙教版（2024）4.6 相似多边形图片ppt课件

这是一份数学浙教版（2024）4.6 相似多边形图片ppt课件，共23页。PPT课件主要包含了形状相同，对应角相等，对应边成比例，做一做，边数不同，对应角不相等，相似多边形的性质，不一定相似如，相似多边形，相似比等内容，欢迎下载使用。

了解相似多边形和相似比的概念；
会根据条件判断两个多边形是否为相似多边形；
掌握相似多边形的性质,能根据相似比进行相关的计算.
图形的相似性给人类的创造发明带来灵感.19世纪末法国机械师克莱兰•阿代尔设计的第三架飞行器的形状就是模仿蝙蝠.
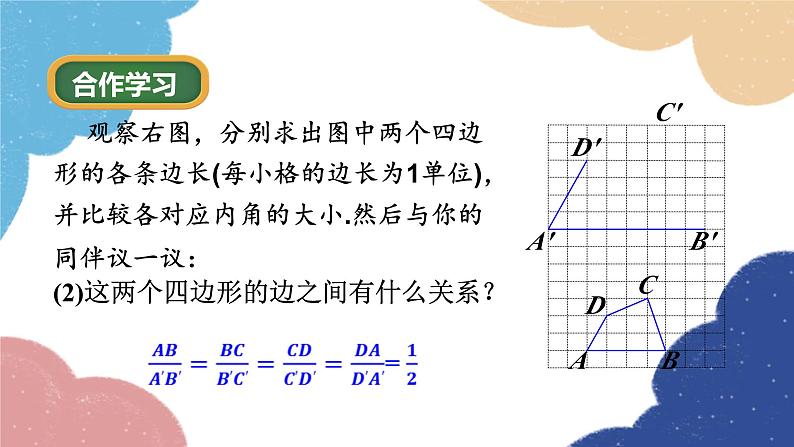
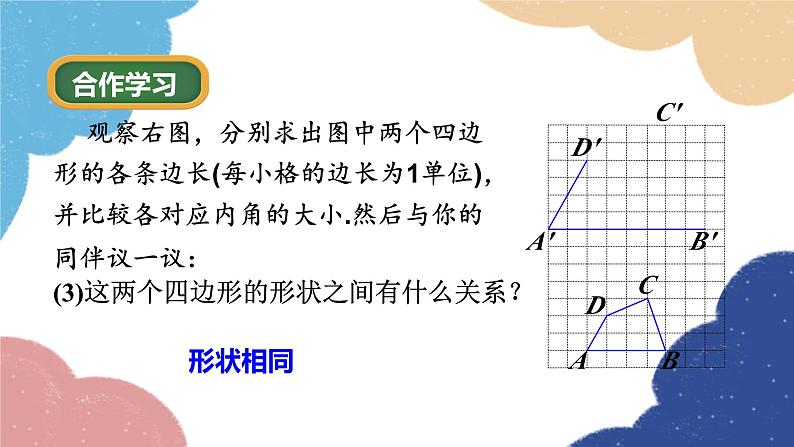
观察右图，分别求出图中两个四边形的各条边长(每小格的边长为1单位)，并比较各对应内角的大小.然后与你的同伴议一议：
(1)这两个四边形的角之间有什么关系？
∠A=∠A′，∠B=∠B′，
∠C=∠C′，∠D=∠D′.
(2)这两个四边形的边之间有什么关系？
(3)这两个四边形的形状之间有什么关系？
一般地，___________，____________的两个多边形叫做相似多边形.相似多边形对应边的比也叫做相似比.
例如，四边形ABCD与四边形A′B′C′D′相似，记做四边形ABCD ∽四边形A′B′C′D′， AB与A′B′的比就是四边形ABCD与四边形A′B′C′D′的相似比.
1、相似符号“∽ ”读做“相似于”；
2、在记两个多边形相似时，要把表示对应角顶点的字母写在对应的位置上.
从四边形ABCD与四边形A′B′C′D′的改变过程中，图形的形状没有改变.
一般地，由一个图形改变为另一个图形，在改变过程中保持形状不变(大小可以改变)，这样的图形改变叫做图形的相似.
解：沿长边对折后所得的矩形纸张和原来的矩形纸张相似.理由如下：如右图，
连接BC与AD的中点F，E，
则EF就把矩形分为全等的两个矩形.
即矩形ABFE与矩形BCDA的对应边成比例.
而两个矩形的对应角相等.所以矩形ABFE与矩形BCDA相似.
观察下列图形，与(1)是相似多边形的是哪个？
两个多边形相似满足的条件
与相似三角形类似，相似多边形有以下性质：相似多边形的周长之比等于相似比；相似多边形的面积之比等于相似比的平方.
1、下列四组图形中，一定相似的是( ) A、正方形和矩形 B、正方形和菱形 C、菱形和菱形 D、正方形与正方形
D、一定相似， 如：
(1)相似比的值与两个多边形的前后顺序有关；(2)相似比为1的两个相似多边形为全等多边形.
3、在如图所示的相似四边形中，AG=DG.　
4、已知，如图，梯形ABCD与梯形A′B′C′D′相似，AD∥BC，A′D′∥B′C′，∠A＝∠A′，AD＝4，A′D′＝6，AB＝6，B′C′＝12，∠C＝60°. (1)求梯形ABCD与梯形A′B′C′D′的相似比k的值；(2)求A′B′和BC的长；(3)求∠D′的大小．
∴A′B′＝9，BC＝8.
(3)由题意知，∠D′＝∠D.∵AD∥BC，∠C＝60°，∴∠D＝180°－∠C＝120°.∴∠D′＝120°.
一般地，对应角相等，对应边成比例的两个多边形叫做相似多边形.
相似多边形的周长之比等于相似比；相似多边形的面积之比等于相似比的平方.
相似多边形对应边的比叫做相似比.