高中数学人教B版 (2019)必修 第四册11.1.3 多面体与棱柱优秀课件ppt

这是一份高中数学人教B版 (2019)必修 第四册11.1.3 多面体与棱柱优秀课件ppt，共26页。PPT课件主要包含了探究点1多面体，多面体的概念，多面体的元素，探究点2棱柱，棱柱的定义，棱柱的元素，棱柱的表示，棱柱的分类，三角形，四边形等内容，欢迎下载使用。
1.了解多面体及其分类、多面体表面积的概念.2.理解棱柱的定义、结构特征及棱柱的分类.（重点）3.知道棱柱表面积的计算公式，能用公式解决简单的实际问题.（重点）
观察我们见过的一些几何体，这些几何体都是多面体.
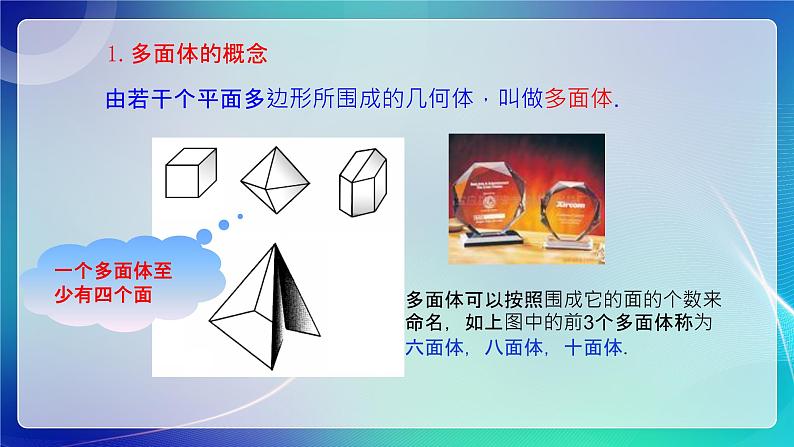
由若干个平面多边形所围成的几何体，叫做多面体.
多面体可以按照围成它的面的个数来命名，如上图中的前3个多面体称为六面体，八面体，十面体.
一个多面体至少有四个面
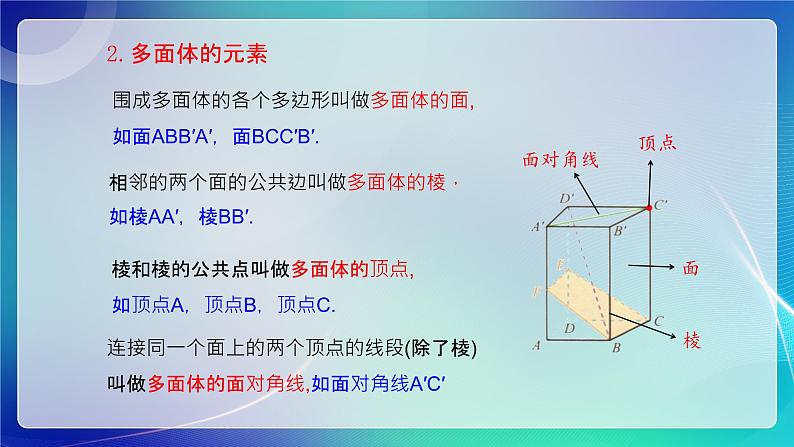
围成多面体的各个多边形叫做多面体的面,如面ABB′A′，面BCC′B′.
相邻的两个面的公共边叫做多面体的棱，如棱AA′，棱BB′.
棱和棱的公共点叫做多面体的顶点,如顶点A，顶点B，顶点C.
连接同一个面上的两个顶点的线段(除了棱)叫做多面体的面对角线,如面对角线A′C′
连接不在同一个面上的两个顶点的线段叫做多面体的体对角线,如对角线BD′，对角线AC′
一个几何体和一个平面相交所得到的平面图形(包含它的内部)，称为这个几何体的一个截面.
多面体的表面积(或全面积)：多面体所有面的面积之和.
3.凸多面体与凹多面体
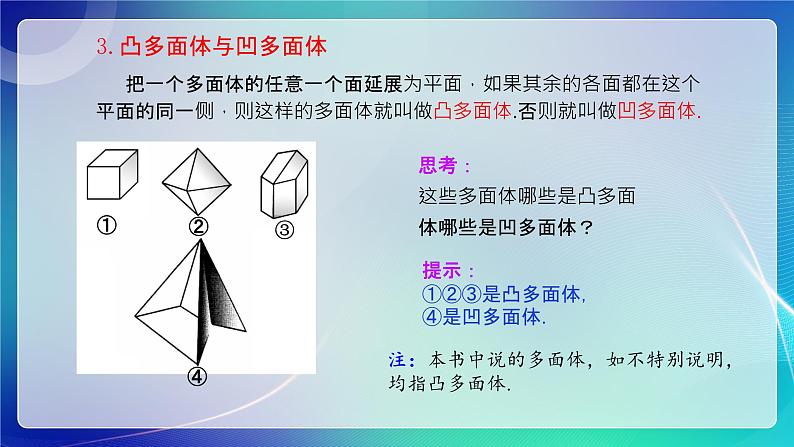
把一个多面体的任意一个面延展为平面，如果其余的各面都在这个平面的同一侧，则这样的多面体就叫做凸多面体.否则就叫做凹多面体.
思考：这些多面体哪些是凸多面体哪些是凹多面体？
提示：①②③是凸多面体，④是凹多面体.
注：本书中说的多面体，如不特别说明，均指凸多面体.
思考1：观察这些棱柱是否可以看作由什么图形平移运动得到的?
由一个多边形（包括图形围成的平面部分）上各点都沿着同一个方向移动相同的距离所形成.
思考2：这些多面体的侧面、上下面分别具有怎样的共性？思考3：这些多面体的顶点具有怎样的共性？
侧面都是平行四边形，上下两个面相互平行.顶点都在这两个面上
你能归纳出一个几何体是棱柱的充要条件是什么吗？
有两个面相互平行，且该多面体的顶点都在这两个面上，其余各面都是平行四边形，这样的多面体称为棱柱.
注意：定义中的条件都要满足，否则此几何体就不一定是棱柱：①两个面互相平行；②所有顶点在这两个面上；③其余各面都是平行四边形.例如图1中的几何体的顶点不满足棱柱的条件.
(1)棱柱的两个互相平行的面称为棱柱的底面(底面水平放置时，分别称为上底面、下底面)；(2)其他各面称为棱柱的侧面，两个侧面的公共边称为棱柱的侧棱；
(3)过棱柱一个底面上的任意一个顶点，作另一个底面的垂线所得到的线段(或它的长度)称为棱柱的高.
（4）棱柱的侧面积：棱柱的所有侧面的面积之和.
(1)用底面上的顶点来表示.(2)用体对角线的两个顶点表示.
思考：下列棱柱的底面分别是什么平面图形?是几棱柱？
分类标准：按侧棱与底面是否垂直侧棱垂直于底面的棱柱称为直棱柱，不是直棱柱的棱柱称为斜棱柱，其中底面是正多边形的直棱柱称为正棱柱.
图中(1)为斜棱柱，(2)(3)为直棱柱，且(3)为正棱柱.
观察下列几何体，回答:
①两个底面多边形间的关系？
②上下底面对应边间的关系？
③侧面是什么平面图形？
⑤平行于底面的截面与底面的关系？
观察下面的几何体，哪些是棱柱？
补充：几种四棱柱（六面体）的关系：
连接 AC,AC′，因为是长方体，所以 在Rt△ABC中， 在Rt△ACC′中,
如图是棱长都为1的直平行六面体ABCD-A1B1C1D1，且∠DAB=60°， (1)写出直线AB与直线CC1，直线AC1与面ABCD，面ABCD与面A1B1C1D1之间的位置关系；(2)求这个直平行六面体的表面积；(3)求线段AC1的长.
因此该底面的面积为 又因为每个侧面的面积为1，所以表面积为
(3)因为是直平行六面体，所以CC1⊥ABCD面，所以CC1⊥AC.在Rt△ACC1中，由
底面为正方形的直棱柱，它的底面对角线长为 ，体对角线长为 ，则这个棱柱的侧面积是(　　)A．2 B．4 C．6 D．8
解析：由已知得底面边长为1，侧棱长为 ∴S侧＝1×2×4＝8.
棱柱的定义与几何特征；长方体中体对角线和棱长的关系；计算棱柱的侧面积.