2024-2025学年上海四中九年级（上）月考数学试卷（10月份）（含解析）

这是一份2024-2025学年上海四中九年级（上）月考数学试卷（10月份）（含解析），共29页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
1．（4分）在中，各边的长度都扩大4倍．那么锐角的正切值
A．扩大4倍B．扩大2倍C．保持不变D．缩小4倍
2．（4分）如图，已知，它们依次交直线、于点、、和点、、，如果，，那么等于
A．B．C．D．
3．（4分）如图，已知在中，，，，垂足为点，那么下列线段的比值不一定等于的是
A．B．C．D．
4．（4分）下列命题中，说法正确的是
A．所有菱形都相似
B．两边对应成比例且有一组角对应相等的两个三角形相似
C．三角形的重心到一个顶点的距离，等于它到这个顶点对边距离的两倍
D．斜边和直角边对应成比例，两个直角三角形相似
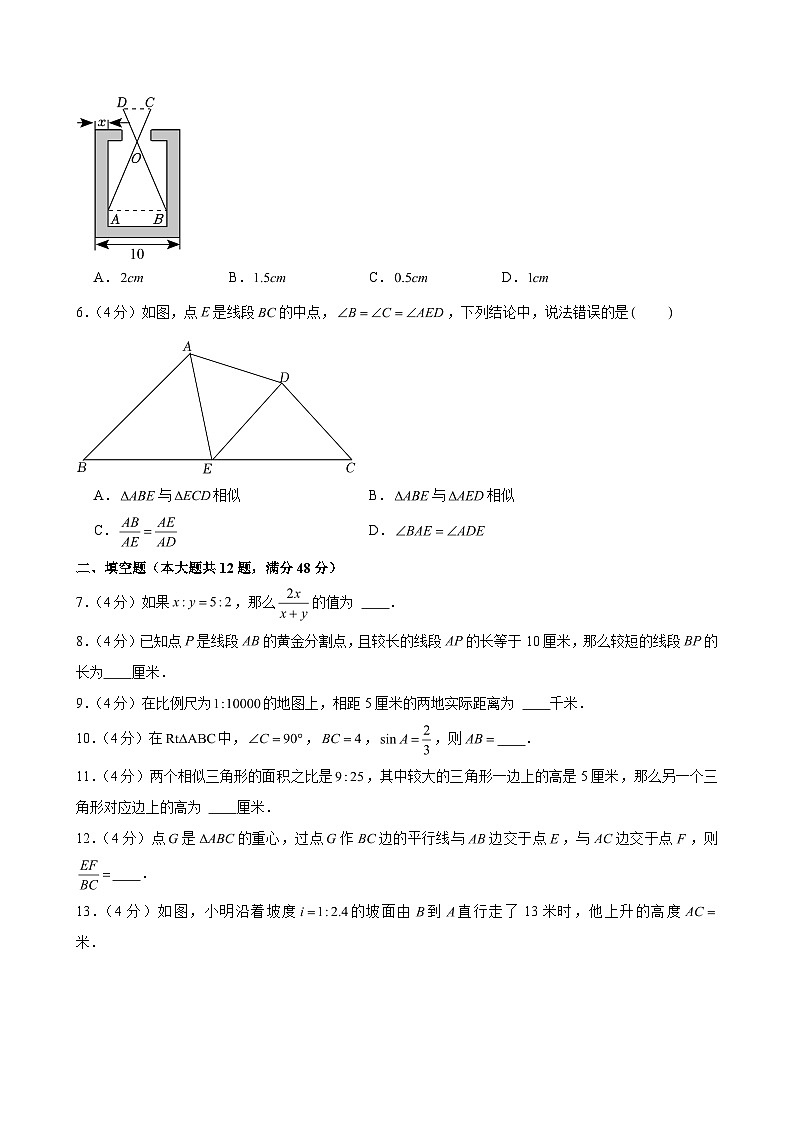
5．（4分）如图，某零件的外径为，用一个交叉卡钳（两条尺长和相等）可测量零件的内孔直径．如果，且量得，则零件的厚度为
A．B．C．D．
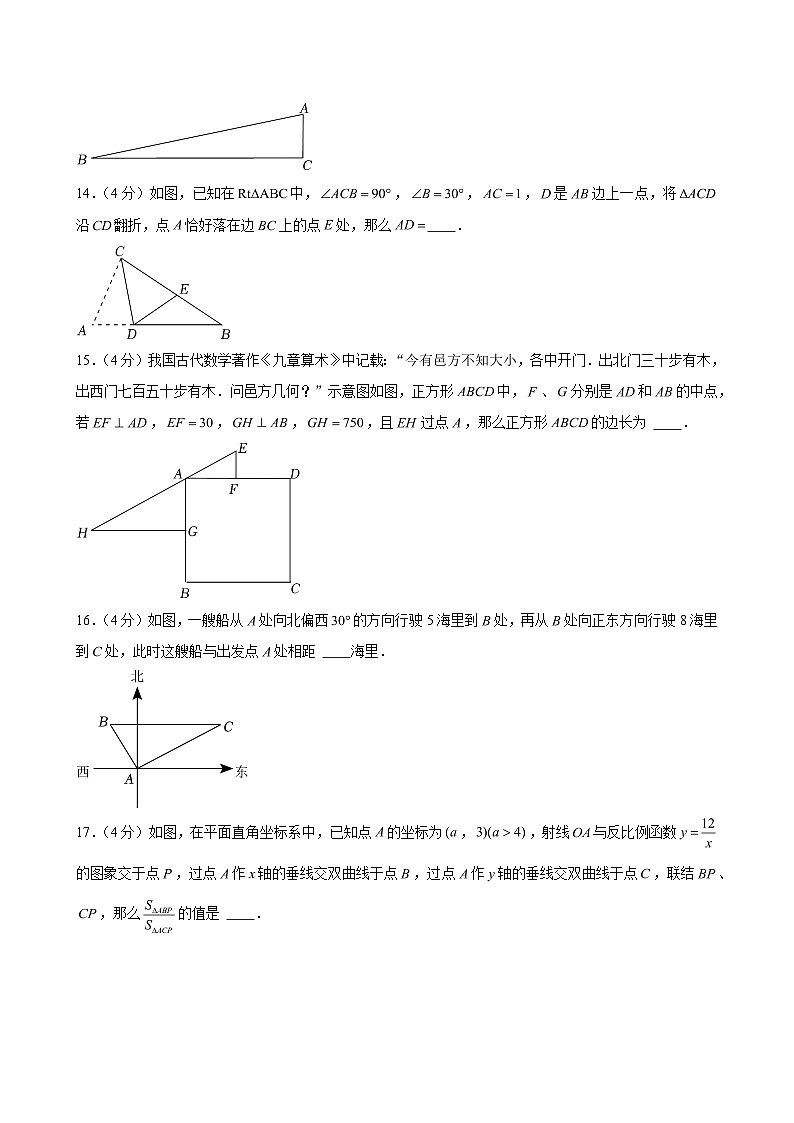
6．（4分）如图，点是线段的中点，，下列结论中，说法错误的是
A．与相似B．与相似
C．D．
二、填空题（本大题共12题，满分48分）
7．（4分）如果，那么的值为 ．
8．（4分）已知点是线段的黄金分割点，且较长的线段的长等于10厘米，那么较短的线段的长为 厘米．
9．（4分）在比例尺为的地图上，相距5厘米的两地实际距离为 千米．
10．（4分）在中，，，，则 ．
11．（4分）两个相似三角形的面积之比是，其中较大的三角形一边上的高是5厘米，那么另一个三角形对应边上的高为 厘米．
12．（4分）点是的重心，过点作边的平行线与边交于点，与边交于点，则 ．
13．（4分）如图，小明沿着坡度的坡面由到直行走了13米时，他上升的高度 米．
14．（4分）如图，已知在中，，，，是边上一点，将沿翻折，点恰好落在边上的点处，那么 ．
15．（4分）我国古代数学著作《九章算术》中记载：“今有邑方不知大小，各中开门．出北门三十步有木，出西门七百五十步有木．问邑方几何？”示意图如图，正方形中，、分别是和的中点，若，，，，且过点，那么正方形的边长为 ．
16．（4分）如图，一艘船从处向北偏西的方向行驶5海里到处，再从处向正东方向行驶8海里到处，此时这艘船与出发点处相距 海里．
17．（4分）如图，在平面直角坐标系中，已知点的坐标为，，射线与反比例函数的图象交于点，过点作轴的垂线交双曲线于点，过点作轴的垂线交双曲线于点，联结、，那么的值是 ．
18．（4分）如图，在中，，，，点是边上一点，将沿着过点的一条直线翻折，使得点落在边上的点处，联结，如果，那么的长为 ．
三、解答题（本大题共7题，满分78分）
19．（10分）计算：．
20．（10分）如图，梯形中，，点是边的中点，联结交于点，的延长线交的延长线于点．
（1）求证：；
（2）若，，求线段的长．
21．（10分）在中，，，．
（1）求证：；
（2）若点为的中点，，，，求的长．
22．（10分）某“综合与实践”小组开展了测量本校旗杆高度的实践活动．他们制订了测量方案，并利用课余时间完成了实地测量．他们在该旗杆底部所在的平地上，选取两个不同测点，分别测量了该旗杆顶端的仰角以及这两个测点之间的距离．为了减小测量误差，小组在测量仰角的度数以及两个测点之间的距离时，都分别测量了两次并取它们的平均值作为测量结果，测量数据如下表（不完整）．
任务一：两次测量，之间的距离的平均值是 ．
任务二：根据以上测量结果，请你帮助该“综合与实践”小组求出学校旗杆的高度．
（参考数据：，，，，，
任务三：该“综合与实践”小组在制定方案时，讨论过“利用物体在阳光下的影子测量旗杆的高度”的方案，但未被采纳．你认为其原因可能是什么？（写出一条即可）
23．（12分）如图，线段是的角平分线，点、点分别在线段、的延长线上，联结、，且．
（1）求证：；
（2）如果，求证：．
24．（12分）如图，在四边形中，，，，是对角线的中点，联结并延长交边于点．
（1）求证：；
（2）若，求的值．
25．（14分）已知，在中，，，点是射线上的动点，点是边上的动点，且，射线交射线于点．
（1）如图，如果，求的值；
（2）联结，如果是以为腰的等腰三角形，求线段的长；
（3）当点在边上时，联结、，，求线段的长．
参考答案
一、选择题（每题4分，满分24分）
1．（4分）在中，各边的长度都扩大4倍．那么锐角的正切值
A．扩大4倍B．扩大2倍C．保持不变D．缩小4倍
解：如图，在中，，则，
，
在中，各边的长度都扩大4倍．那么锐角的正切值保持不变，
故选：．
2．（4分）如图，已知，它们依次交直线、于点、、和点、、，如果，，那么等于
A．B．C．D．
解：，
，
即，
．
故选：．
3．（4分）如图，已知在中，，，，垂足为点，那么下列线段的比值不一定等于的是
A．B．C．D．
解：、不一定等于，故符合题意；
、是直角三角形，，正确，故不符合题意；
、，，，，正确，故不符合题意；
、是直角三角形，，正确，故不符合题意．
故选：．
4．（4分）下列命题中，说法正确的是
A．所有菱形都相似
B．两边对应成比例且有一组角对应相等的两个三角形相似
C．三角形的重心到一个顶点的距离，等于它到这个顶点对边距离的两倍
D．斜边和直角边对应成比例，两个直角三角形相似
解：、所有的菱形不相似，故错误，不符合题意；
、两边对应成比例且夹角相等的两个三角形相似，故错误，不符合题意；
、三角形的重心到一个顶点的距离等于它到对边中点距离的两倍，故错误，不符合题意；
、斜边和直角边对应成比例的两个直角三角形是相似的，故该选项正确，符合题意；
故选：．
5．（4分）如图，某零件的外径为，用一个交叉卡钳（两条尺长和相等）可测量零件的内孔直径．如果，且量得，则零件的厚度为
A．B．C．D．
解：，，
，
，
．
．
某零件的外径为，
零件的厚度为：，
故选：．
6．（4分）如图，点是线段的中点，，下列结论中，说法错误的是
A．与相似B．与相似
C．D．
解：，，
，
，
，
，
，
，
，
，
，
，
故选项，，正确，
故选：．
二、填空题（本大题共12题，满分48分）
7．（4分）如果，那么的值为 ．
解：，
，
．
故答案为：．
8．（4分）已知点是线段的黄金分割点，且较长的线段的长等于10厘米，那么较短的线段的长为 厘米．
解：设线段的长为，
点是线段的黄金分割点，较长的线段的长等于10厘米，
，
解得，，
较短的线段的长（厘米），
故答案为：．
9．（4分）在比例尺为的地图上，相距5厘米的两地实际距离为 0.5 千米．
解：根据：比例尺图上距离：实际距离，
设两地实际距离为厘米，得：，
相距5厘米的两地的实际距离是（厘米）（千米），
故答案为：0.5．
10．（4分）在中，，，，则 6 ．
解：在中，，，，
，
，
故答案为：6．
11．（4分）两个相似三角形的面积之比是，其中较大的三角形一边上的高是5厘米，那么另一个三角形对应边上的高为 3 厘米．
解：设另一个三角形对应边上的高为厘米，
两个相似三角形的面积之比是，其中较大的三角形一边上的高是5厘米，
，
解得：，
另一个三角形对应边上的高为3厘米，
故答案为：3．
12．（4分）点是的重心，过点作边的平行线与边交于点，与边交于点，则 ．
解：连接交于点，
，
，
是的重心，
，
是中点，
，
，
故答案为：．
13．（4分）如图，小明沿着坡度的坡面由到直行走了13米时，他上升的高度 5 米．
解：坡度，
与的比为，
设米，则米，
由勾股定理，得．
解得．
故答案为：5．
14．（4分）如图，已知在中，，，，是边上一点，将沿翻折，点恰好落在边上的点处，那么 ．
解：，，
，
沿翻折，点恰好落在边上的点处，
，，，
，
，
，
在中，，
，，
，
，
．
故答案为：．
15．（4分）我国古代数学著作《九章算术》中记载：“今有邑方不知大小，各中开门．出北门三十步有木，出西门七百五十步有木．问邑方几何？”示意图如图，正方形中，、分别是和的中点，若，，，，且过点，那么正方形的边长为 300 ．
解：、分别是和的中点，，
，，
，
由题意可得，，
，
即，
解得：，
．
故答案为：300．
16．（4分）如图，一艘船从处向北偏西的方向行驶5海里到处，再从处向正东方向行驶8海里到处，此时这艘船与出发点处相距 7 海里．
解：如图：
，
，
，海里，
海里，海里，
（海里），
（海里），
故答案为：7．
17．（4分）如图，在平面直角坐标系中，已知点的坐标为，，射线与反比例函数的图象交于点，过点作轴的垂线交双曲线于点，过点作轴的垂线交双曲线于点，联结、，那么的值是 1 ．
解：设的解析式为，
，
，
，
联立，
解得，
，，
过点作交于点，交于点，
，，
，，，，
，
，
；
方法二：过点作轴的垂线，垂足为，过点作轴的垂线，垂足为，过点作，过点作，
点、在反比例函数图象上，
，
，
，
，
，，
，
，，
，
；
故答案为：1．
18．（4分）如图，在中，，，，点是边上一点，将沿着过点的一条直线翻折，使得点落在边上的点处，联结，如果，那么的长为 ．
解：根据题意如图所示：
在中，，
，，
，
根据折叠的性质可知，
，，
，
，
平分，
设，则，
如图，过点作于点，于点，
，
，
，
，，
，
，
，
，
，
，
，
，，
，
，
，
，
，
．
故答案为：．
三、解答题（本大题共7题，满分78分）
19．（10分）计算：．
解：
．
20．（10分）如图，梯形中，，点是边的中点，联结交于点，的延长线交的延长线于点．
（1）求证：；
（2）若，，求线段的长．
【解答】（1）证明：，
△△，
，
点是边的中点，
，
，
；
（2）解：，
△△，
，
由（1）知，，
，
设，
，，
，
解得，（不合题意，舍去），
．
21．（10分）在中，，，．
（1）求证：；
（2）若点为的中点，，，，求的长．
解：（1），，
，
，
，
，
，
，
；
（2）；
，是直角三角形，
，
，
，
，
，
，
，
，
，
．
22．（10分）某“综合与实践”小组开展了测量本校旗杆高度的实践活动．他们制订了测量方案，并利用课余时间完成了实地测量．他们在该旗杆底部所在的平地上，选取两个不同测点，分别测量了该旗杆顶端的仰角以及这两个测点之间的距离．为了减小测量误差，小组在测量仰角的度数以及两个测点之间的距离时，都分别测量了两次并取它们的平均值作为测量结果，测量数据如下表（不完整）．
任务一：两次测量，之间的距离的平均值是 5.5 ．
任务二：根据以上测量结果，请你帮助该“综合与实践”小组求出学校旗杆的高度．
（参考数据：，，，，，
任务三：该“综合与实践”小组在制定方案时，讨论过“利用物体在阳光下的影子测量旗杆的高度”的方案，但未被采纳．你认为其原因可能是什么？（写出一条即可）
解：任务一：，
故答案为：5.5；
任务二：设，
在中，，，
，
，
在中，，，
，，
，
，
，
（米，
答：旗杆的高度为14.7米；
任务三：没有太阳光或旗杆底部不可能到达．
23．（12分）如图，线段是的角平分线，点、点分别在线段、的延长线上，联结、，且．
（1）求证：；
（2）如果，求证：．
【解答】证明：（1）是的角平分线，
，
，
，
，
，
，
，
；
（2），
，
，，
，
，
，
，
，
，
，
，
，
，
，
，
，
，
，，
．
24．（12分）如图，在四边形中，，，，是对角线的中点，联结并延长交边于点．
（1）求证：；
（2）若，求的值．
【解答】（1）证明：，
，
，
，
是的中点，，
，
，
，
；
（2）解：，
，
，
，
过点作于点，
设，则，
在中，，，，
．
25．（14分）已知，在中，，，点是射线上的动点，点是边上的动点，且，射线交射线于点．
（1）如图，如果，求的值；
（2）联结，如果是以为腰的等腰三角形，求线段的长；
（3）当点在边上时，联结、，，求线段的长．
解：（1），，
，，
，
又，
，
，
，
，
，
，，
，
；
（2）如图1，当点在上时，
，是等腰三角形，
，
由（1）可知：，
，
，
，
，
；
当点在线段的延长线上时，如图2，
是等腰三角形，
，
，
，
，
，
，
，
，
由（1）可知：，
，
，
，
，
，
，
综上所述：线段的长为或；
（3）如图3，当点在线段上时，
，，
，
，
，，
，
，
，
，，
，
，
，
，
或（不合题意舍去），
．
课题
测量旗杆的高度
成员
组长： 组员：，，
测量工具
测量角度的仪器，皮尺等
测量示意图
说明：线段表示学校旗杆，测量角度的仪器的高度，测点，与在同一条水平直线上，，之间的距离可以直接测得，且点，，，，，都在同一竖直平面内，点，，在同一条直线上，点在 上．
测量数据
测量项目
第一次
第二次
平均值
的度数
的度数
，之间的距离
课题
测量旗杆的高度
成员
组长： 组员：，，
测量工具
测量角度的仪器，皮尺等
测量示意图
说明：线段表示学校旗杆，测量角度的仪器的高度，测点，与在同一条水平直线上，，之间的距离可以直接测得，且点，，，，，都在同一竖直平面内，点，，在同一条直线上，点在 上．
测量数据
测量项目
第一次
第二次
平均值
的度数
的度数
，之间的距离