初中数学浙教版（2024）九年级上册1.1 二次函数课堂检测

这是一份初中数学浙教版（2024）九年级上册1.1 二次函数课堂检测，共68页。
题型一：图像法解一元二次不等式
题型二：利用不等式求自变量或函数值的范围
题型三：根据交点确定不等式的解集
【考点剖析】
题型一：图像法解一元二次不等式
一、单选题
1．（2023秋·浙江嘉兴·九年级统考期末）我们规定：形如的函数叫作“型”函数．如图是“型”函数的图象，根据图象，以下结论：
①图象关于轴对称；
②不等式的解集是或；
③方程有两个实数解时．正确的是（ ）
A．①②．B．②③．C．①③．D．①②③．
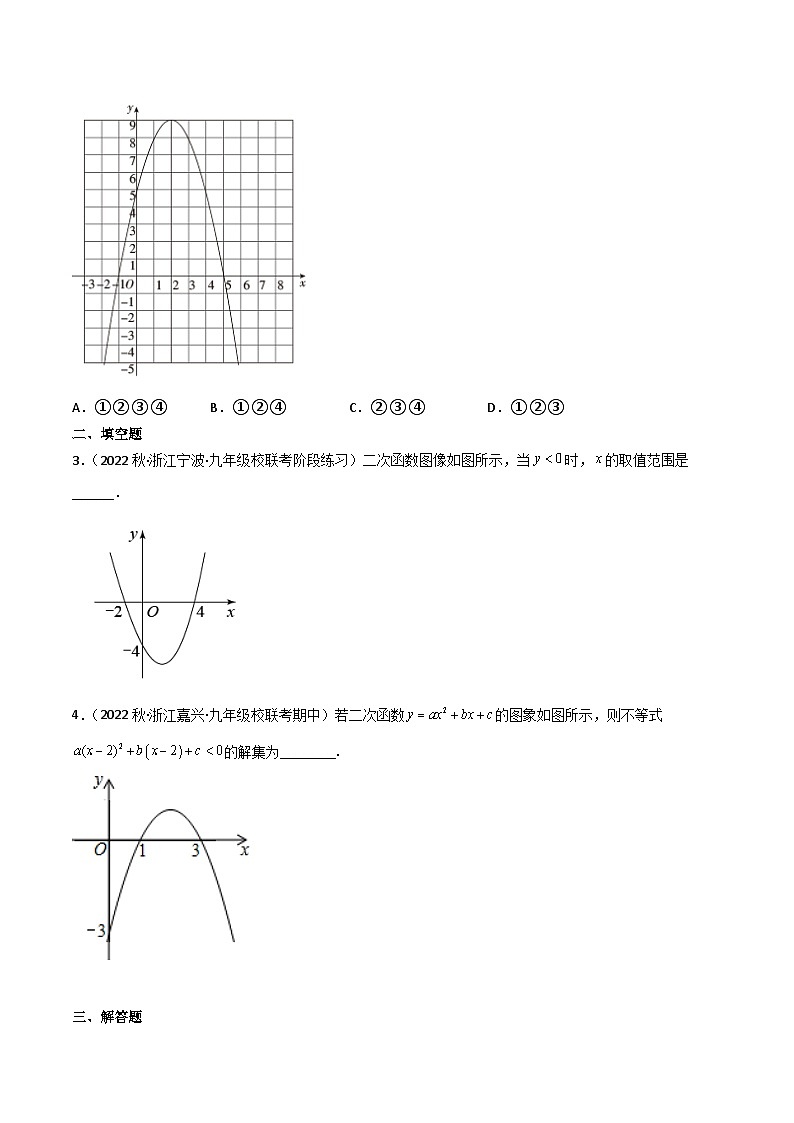
2．（2022春·浙江绍兴·九年级专题练习）知函数y＝a|x﹣2|+x+b（a，b为常数）．当x＝3时，y＝0，当x＝0时，y＝﹣1，对该函数及其图象，笑笑进行探究，得到了以下结论：①a＝2；②b＝﹣5；③该函数当x≥2时，y随x的增大而增大；④结合图象，可以直接写出不等式a|x﹣2|+x+b≥﹣x2+4x+5为x≥．以上结论正确的是（ ）
A．①②③④B．①②④C．②③④D．①②③
二、填空题
3．（2022秋·浙江宁波·九年级校联考阶段练习）二次函数图像如图所示，当时，的取值范围是______．
4．（2022秋·浙江嘉兴·九年级校联考期中）若二次函数的图象如图所示，则不等式的解集为________．
三、解答题
5．（2022秋·浙江杭州·九年级校联考阶段练习）在平面直角坐标系内，二次函数（a为常数）．
(1)若函数y的图象经过点，求函数的表达式．
(2)若的图象与一次函数的图象有两个交点，横坐标分别为﹣1，2，请直接写出当时x的取值范围．
(3)已知在函数的图象上，当时，求证：．
6．（2022秋·浙江杭州·九年级校考阶段练习）已知二次函数
(1)求出该函数图象的顶点坐标，图象与轴的交点坐标
(2)当x在什么范围内时，y随x的增大而增大?
(3)当x在什么范围内时，?
7．（2022秋·浙江绍兴·九年级校考阶段练习）已知抛物线的部分图象如图所示．
(1)求b，c的值；
(2)直接写出该二次函数当时，x的取值范围．
8．（2022秋·浙江杭州·九年级校考阶段练习）已知二次函数(，是常数，且)的图象经过点．
(1)求该函数图象的对称轴；
(2)若该函数图象还经过点
①求该函数的解析式；
②当时，直接写出的取值范围．
9．（2023·浙江·九年级专题练习）已知二次函数．
(1)若，且函数图象经过，两点，求此二次函数的解析式；并根据图象直接写出函数值时自变量x的取值范围；
(2)在（1）的条件下，已知抛物线与x轴交于A，B两点（点A在点B的左侧），将这条抛物线向右平移m（）个单位，平移后的抛物线于x轴交于C，D两点（点C在点D的左侧），若B，C是线段的三等分点，求m的值．
(3)已知 ，当，q（p，q是实数，）时，该函数对应的函数值分别为P，Q．若，求证．
10．（2022秋·浙江宁波·九年级统考期末）如图，已知二次函数的图象过，和三点．
(1)求这个二次函数及直线的函数关系式；
(2)直接写出不等式的解；
(3)点是抛物线对称轴上的一个动点，当的值最小时，求点的坐标．
11．（2022·浙江·九年级专题练习）如图，在平面直角坐标系中，已知，，点在轴正半轴上，且．抛物线经过点，．
(1)求这条抛物线的解析式，并直接写出当时的取值范围；
(2)将抛物线先向右平移个单位，再向上平移2个单位，此时点恰好落在线段上，求的值．
12．（2023·浙江·九年级专题练习）如图，直线y=x+m和抛物线y=x2+bx+c都经过点A（1，0），B（3，2）．
(1)求m的值和抛物线的解析式；
(2)求不等式x2+bx+c＞x+m的解集．（直接写出答案）
13．（2022秋·浙江杭州·九年级校考期中）已知：直线经过抛物线的顶点．
(1)求抛物线的表达式；
(2)求此抛物线与坐标轴的三个交点所构成的三角形的面积；
(3)请直接写出不等式的解集．
14．（2022·浙江杭州·统考一模）在直角坐标系中，设函数（a，b是常数，）．
(1)已知函数的图象经过点（1，2）和，求函数的表达式．
(2)若函数图象的顶点在函数的图象上，求证：．
(3)已知点，在函数的图象上，且．当时，求自变量x的取值范围．
题型二：利用不等式求自变量或函数值的范围
一、单选题
1．（2022秋·浙江舟山·九年级校联考期中）已知满足，且，则的取值范围是（ ）
A．B．C．D．
2．（2022·浙江·九年级专题练习）已知函数y＝，当a≤x≤b时，﹣≤y≤2，则b﹣a的最大值为（ ）
A．B．C．D．2
3．（2022·浙江宁波·一模）已知A，B两点的坐标分别为，，线段上有一动点，过点M作x轴的平行线交抛物线于两点（P在Q的左侧）．若恒成立，则a的取值范围为（ ）
A．B．C．D．
4．（2023秋·浙江湖州·九年级统考期末）抛物线与轴交于点，过点作直线垂直于轴，将抛物线在轴右侧的部分沿直线翻折，其余部分保持不变，组成图形，点，为图形上两点，若，则的取值范围是（ ）
A．B．C．D．
二、填空题
5．（2022秋·浙江·九年级期中）对于一个函数，当自变量x取n时，函数值y等于2﹣n，我们称n为这个函数的“二合点”，如果二次函数y＝ax2+x﹣1有两个相异的二合点x1，x2，且x1＜x2＜1，则a的取值范围是_____．
6．（2022秋·浙江金华·九年级校联考阶段练习）新定义：若一个点的纵坐标是横坐标的2倍，则称这个点为二倍点．若二次函数（c为常数）在的图象上存在两个二倍点，则c的取值范围是_______．
三、解答题
7．（2022秋·浙江杭州·九年级杭州市丰潭中学校考阶段练习）已知二次函数的图象经过点，，且当，时，．
(1)求的值；
(2)若，也是该二次函数图象上的两个点，且，求实数的取值范围；
(3)若点不在该二次函数的图象上，求的取值范围．
8．（2022秋·浙江金华·九年级义乌市绣湖中学教育集团校联考期中）某“数学兴趣小组”根据学习函数的经验，对函数的图象和性质进行了探究，探究过程如下，请补充完整：
获得图象：
计算x与y的几组对应值，列表如下：
(1)如图，在直角坐标系中画出了函数将这个图象补画完整．
探究性质：
(2)根据函数图象，写出该函数的一个正确结论：
解决问题：
(3)若过定点的直线与函数（）的图象只有一个交点，请结合函数图象求出t的取值范围．
9．（2022秋·浙江金华·九年级校联考期中）某“数学兴趣小组”根据学习函数的经验，对函数的图象和性质进行了探究，探究过程如下，请补充完整：
(1)x与y的几组对应值如下表，其中m=________．
(2)如图，在直角坐标系中画出了函数的部分图象，用描点法将这个图象补画完整．
(3)结合函数图象，解决下列问题：
①解不等式：；
②若直线与函数的图象只有一个的交点，求t的取值范围．
10．（2022秋·浙江台州·九年级统考期末）二次函数的自变量与函数值的部分对应值如下表：
(1)二次函数的图象开口向______，对称轴为直线______．
(2)求该二次函数的解析式．
(3)当时，求y的取值范围，
11．（2022秋·浙江杭州·九年级校联考期中）已知二次函数经过点，，且最大值为4．
(1)求二次函数的解析式；
(2)在平面直角坐标系中，画出二次函数的图象；
(3)当时，结合函数图象，直接写出y的取值范围．
12．（2023春·浙江宁波·九年级校联考竞赛）已知拋物线．
(1)若此拋物线与轴只有一个公共点且过点．
①求此抛物线的解析式；
②直线与该抛物线交于点和点．若，求的取值范围．
(2)若，将此抛物线向上平移个单位得到新抛物线，当时，；当时，．试比较与1的大小，并说明理由．
题型三：根据交点确定不等式的解集
一、单选题
1．（2023秋·浙江杭州·九年级统考期末）已知二次函数，函数值与自变量的部分对应值如表：
则当时，的取值范围是（ ）
A．B．
C．或D．或
2．（2023秋·浙江温州·九年级期末）二次函数的图象与一次函数的图象没有交点，则b的取值范围是（ ）
A．B．C．或D．
二、填空题
3．（2023春·浙江金华·九年级校联考阶段练习）如图，抛物线（a，b，c为常数，且）交x轴于，两点，则不等式的解集为_______．
4．（2023秋·浙江杭州·九年级期中）如图，二次函数与反比例函数的图象相交于点三个点，则不等式的解是____．
三、解答题
5．（2023·浙江宁波·统考一模）如图，二次函数的图象与x轴相交于点，，与轴相交于点．
(1)求二次函数的表达式和其图象的顶点坐标．
(2)若一次函数的图象经过二次函数图象的顶点，请根据图象直接写出当时的取值范围．
6．（2023秋·浙江湖州·九年级统考期末）已知二次函数．
(1)求此二次函数图象的顶点坐标；
(2)当函数值时，求自变量x的取值范围．
7．（2023秋·浙江宁波·九年级统考期末）如图，在平面直角坐标系中，一次函数的图象与二次函数的图象交于、两点．
(1)求与的函数关系式；
(2)直接写出当时，的取值范围；
(3)点为一次函数图象上一点，点的横坐标为，若将点向右平移2个单位，再向上平移4个单位后刚好落在二次函数的图象上，求的值．
8．（2023春·浙江杭州·九年级专题练习）若二次函数的图象的顶点在一次函数的图象上，则称为的伴随函数，如是的伴随函数．
(1)若函数先向右平移2个单位，再向上平移1个单位后是的伴随函数，求的值
(2)若函数的伴随函数与轴只有一个交点，求当时，的取值范围．
9．（2023春·浙江杭州·九年级专题练习）已知抛物线与一次函数有两个交点，且交点的横坐标分别为，．
(1)根据图象直接写出，当时，的取值范围为 ；
(2)将抛物线向上平移，使其顶点落在一次函数图象上，求平移后图象所对应的二次函数的表达式．
10．（2023·浙江·九年级专题练习）已知函数（a是常数，且）．
(1)若点在二次函数y的图象上，
①求该函数的表达式和顶点坐标；
②若点和在函数的图象上，且，求的取值范围；
(2)若函数y的图象过和两点，且当时，始终都有，求a的取值范围．
11．（2023春·浙江金华·九年级义乌市绣湖中学教育集团校考阶段练习）已知二次函数，．
(1)若二次函数的图象经过A，C两点，求二次函数的解析式．
(2)若二次函数图象与y轴正半轴有交点，试判断二次函数的图象与x轴的交点个数，并说明理由．
(3)若二次函数图象经过点C，设P为二次函数图象上的一个动点，当时，点P关于x轴的对称点都在直线的下方，求m的取值范围．
12．（2023·浙江杭州·九年级专题练习）已知二次函数的图象经过点．
(1)若该二次函数图象与轴的一个交点是．
①求二次函数的表达式：
②当时，函数最大值为，最小值为．若，求t的值；
(2)对于该二次函数图象上的两点，当时，始终有．求的取值范围．
13．（2023春·浙江杭州·九年级杭州市杭州中学校考阶段练习）平面直角坐标系中有函数的图象向右平移2个单位，再向上平移1个单位后与的图象重合，经过与轴的交点以及的顶点．
(1)求和的表达式；
(2)当时，试比较与的大小：
(3)当时，均随着的增大而增大，求实数的最大值．
x
•••
•••
y
•••
•••
x
……
-4
-3
-2
-1
0
1
2
3
4
……
y
……
5
0
-3
m
-3
0
1
0
-3
……
…
0
1
2
…
…
2
7
…
重难点专项突破02二次函数与不等式（3种题型）
【题型细目表】
题型一：图像法解一元二次不等式
题型二：利用不等式求自变量或函数值的范围
题型三：根据交点确定不等式的解集
【考点剖析】
题型一：图像法解一元二次不等式
一、单选题
1．（2023秋·浙江嘉兴·九年级统考期末）我们规定：形如的函数叫作“型”函数．如图是“型”函数的图象，根据图象，以下结论：
①图象关于轴对称；
②不等式的解集是或；
③方程有两个实数解时．正确的是（ ）
A．①②．B．②③．C．①③．D．①②③．
【答案】A
【分析】根据函数图象直接判断A，根据二次函数与坐标轴的交点分析，根据对称性可得轴与轴左边的交点为，即可判断B，根据图象可知当或时，原方程有两个实数根，据此即可求解．
【详解】解：由函数图象可知，此图像关于轴对称，故①正确；
②对称性可得轴与轴左边的交点为，则不等式即的解集是或，故②正确；
③∵，当时，，顶点坐标为和，且与轴交于点，
∴当或时，方程有两个实数解，
故③不正确，
故选：A．
【点睛】本题考查了二次函数图象的性质，掌握二次函数的性质是解题的关键．
2．（2022春·浙江绍兴·九年级专题练习）知函数y＝a|x﹣2|+x+b（a，b为常数）．当x＝3时，y＝0，当x＝0时，y＝﹣1，对该函数及其图象，笑笑进行探究，得到了以下结论：①a＝2；②b＝﹣5；③该函数当x≥2时，y随x的增大而增大；④结合图象，可以直接写出不等式a|x﹣2|+x+b≥﹣x2+4x+5为x≥．以上结论正确的是（ ）
A．①②③④B．①②④C．②③④D．①②③
【答案】D
【分析】①②由题意得：，即可求解；
③函数的表达式为，当时，，当时，，根据函数表达式画出函数图象，即可求解；
④观察函数图象即可求解．
【详解】解：由题意得： ，解得，故①②正确；
因此函数的表达式为，
当时，，
当时，；
根据函数表达式画出函数图象如下：
从图象看，当时，随的增大而增大，故③正确；
（3）从图象看两个函数交于点、，
联立和得：，解得（负值已舍去），
即点 的横坐标为，
从函数图象看，不等式的解集为或，故④错误；
故选：D．
【点睛】本题考查的是二次函数与不等式（组，主要要求学生通过观察函数图象的方式来求解不等式，正确画出函数图象是本题解题的关键．
二、填空题
3．（2022秋·浙江宁波·九年级校联考阶段练习）二次函数图像如图所示，当时，的取值范围是______．
【答案】
【分析】利用抛物线与x轴的两个交点坐标，然后写出抛物线在x轴下方所对应的自变量的范围即可．
【详解】解：∵抛物线与x轴的一个交点坐标为（，0），与x轴的另一个交点坐标为（3，0），
∴当时，．
故答案为：．
【点睛】本题考查了求抛物线与x轴的交点和图像法解一元二次不等式，解题的关键是通过数形结合的方法求解一元二次不等式．
4．（2022秋·浙江嘉兴·九年级校联考期中）若二次函数的图象如图所示，则不等式的解集为________．
【答案】或
【分析】直接利用函数图象即可得出结论．
【详解】∵由函数图象可知，当x3时，函数图象在x轴的下方，
∴函数y=a（x-2）2+b（x-2）+c的图象与x轴的交点为3，5，（把x-2作为一个整体，代入上面的函数中，）
∴不等式a（x-2）2+b（x-2）+c