2022-2023学年北京市和平街一中高二（上）期中数学试卷

这是一份2022-2023学年北京市和平街一中高二（上）期中数学试卷，共19页。试卷主要包含了单项选择题，填空题，解答题等内容，欢迎下载使用。
1．（4分）直线x+y+＝0的倾斜角为（ ）
A．30°B．45°C．60°D．135°
2．（4分）已知直线l的方向向量为，平面α的法向量为，则“”是“l∥α”的（ ）
A．充分不必要条件
B．必要不充分条件
C．充要条件
D．既不充分也不必要条件
3．（4分）已知圆，圆，那么两圆的位置关系是（ ）
A．相交B．外离C．外切D．内含
4．（4分）已知点A（1，2，﹣1），B（2，t，0），O为坐标原点，且，则＝（ ）
A．B．C．D．
5．（4分）在同一平面直角坐标系中，直线l1：ax+y+b＝0和直线l2：bx+y+a＝0有可能是（ ）
A．B．
C．D．
6．（4分）已知直线mx+4y﹣2＝0与2x﹣5y+n＝0互相垂直，垂足为P（1，p），则m﹣n+p的值是（ ）
A．24B．20C．0D．﹣4
7．（4分）若表示焦点在x轴上的椭圆，则实数a的取值范围是（ ）
A．（﹣2，+∞）B．（﹣∞，﹣1）∪（2，+∞）
C．（﹣2，﹣1）∪（2，+∞）D．任意实数R
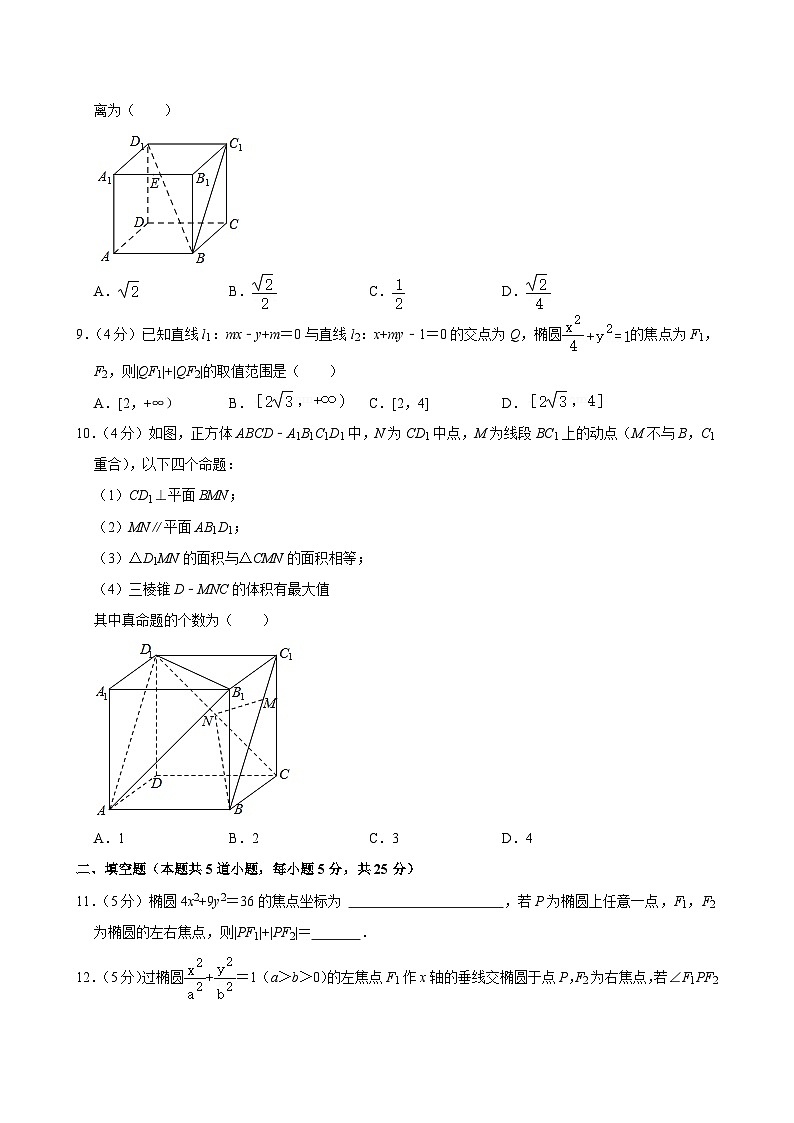
8．（4分）在棱长为1的正方体ABCD﹣A1B1C1D1中，点E为棱A1B1的中点，则点E到平面BC1D1的距离为（ ）
A．B．C．D．
9．（4分）已知直线l1：mx﹣y+m＝0与直线l2：x+my﹣1＝0的交点为Q，椭圆的焦点为F1，F2，则|QF1|+|QF2|的取值范围是（ ）
A．[2，+∞）B．C．[2，4]D．
10．（4分）如图，正方体ABCD﹣A1B1C1D1中，N为CD1中点，M为线段BC1上的动点（M不与B，C1重合），以下四个命题：
（1）CD1⊥平面BMN；
（2）MN∥平面AB1D1；
（3）△D1MN的面积与△CMN的面积相等；
（4）三棱锥D﹣MNC的体积有最大值
其中真命题的个数为（ ）
A．1B．2C．3D．4
二、填空题（本题共5道小题，每小题5分，共25分）
11．（5分）椭圆4x2+9y2＝36的焦点坐标为 ，若P为椭圆上任意一点，F1，F2为椭圆的左右焦点，则|PF1|+|PF2|＝ ．
12．（5分）过椭圆+＝1（a＞b＞0）的左焦点F1作x轴的垂线交椭圆于点P，F2为右焦点，若∠F1PF2＝60°，则椭圆的离心率为 ．
13．（5分）能说明“直线x﹣y+m＝0与圆x2+y2+4x﹣2y＝0有两个不同的交点”是真命题的一个m的值为 ．
14．（5分）已知圆C过点A（﹣1，2），B（1，0），则圆心C到原点距离的最小值为 ．
15．（5分）数学中有许多寓意美好的曲线，曲线C：（x2+y2）3＝4x2y2被称为“四叶玫瑰线”（如图所示）．给出下列三个结论：
①曲线C关于直线y＝x对称；
②曲线C上任意一点到原点的距离都不超过1；
③存在一个以原点为中心、边长为的正方形，使得曲线C在此正方形区域内（含边界）．
其中，正确结论的序号是 ．
三、解答题（本题共6道小题，共85分.要求有演算或推理步骤）
16．（13分）已知△ABC的顶点坐标分别是A（﹣1，5），B（﹣2，﹣1），C（4，3）．M为BC边的中点．
（Ⅰ）求中线AM的方程；
（Ⅱ）求经过点C且与直线AB平行的直线方程．
17．（13分）如图，在正方体ABCD﹣A1B1C1D1中，E为DD1的中点．
（Ⅰ）求证：BD1∥平面ACE；
（Ⅱ）求直线AD与平面ACE所成角的正弦值．
18．（14分）求满足下列条件的曲线方程．
（1）求过点A（3，5）且与圆O：x2+y2﹣2x﹣4y+1＝0相切的直线方程；
（2）求圆心在直线3x﹣y＝0上，与x轴相切，且被直线x﹣y＝0截得的弦长为的圆的方程．
19．（15分）在三棱锥P﹣ABC中，平面PAC⊥平面ABC，△PAC为等腰直角三角形，PA⊥PC，AC⊥BC，BC＝2AC＝4，M为AB的中点．
（Ⅰ）求证：AC⊥PM；
（Ⅱ）求二面角C﹣PA﹣B的余弦值；
（Ⅲ）在线段PB上是否存在点N使得平面CMN⊥平面PAB？若存在，求出的值，若不存在，说明理由．
20．（15分）已知椭圆G：，斜率为1的直线l与椭圆G交于A，B两点，以AB为底边作等腰三角形，顶点为P（﹣3，2）．
（Ⅰ）求椭圆G的离心率；
（Ⅱ）求△PAB的面积．
21．（15分）已知椭圆E：+＝1（a＞b＞0）经过点（﹣1，），其离心率e＝．
（Ⅰ）求椭圆E的方程；
（Ⅱ）设动直线l：y＝kx+m与椭圆C相切，切点为T，且l与直线x＝﹣4相交于点S．
试问：在x轴上是否存在一定点，使得以ST为直径的圆恒过该定点？若存在，求出该点的坐标；若不存在，请说明理由．
2022-2023学年北京市和平街一中高二（上）期中数学试卷
参考答案与试题解析
一、单项选择题（本题共10道小题，每小题4分，共40分）
1．（4分）直线x+y+＝0的倾斜角为（ ）
A．30°B．45°C．60°D．135°
【分析】根据题意，设直线x+y+＝0的倾斜角为θ，由直线斜率的定义可得直线x+y+＝0的斜率，结合直线的斜率与倾斜角的关系可得tanθ＝﹣1，结合直线倾斜角的范围，计算可得答案．
【解答】解：设直线x+y+＝0的倾斜角为θ，则0°≤θ＜180°，
直线x+y+＝0变形可得y＝﹣x﹣，其斜率为﹣1，
则有tanθ＝﹣1，且0°≤θ＜180°，
则θ＝135°，
故选：D．
【点评】本题考查直线的倾斜角的定义与计算，关键是理解直线的倾斜角与直线斜率的关系．
2．（4分）已知直线l的方向向量为，平面α的法向量为，则“”是“l∥α”的（ ）
A．充分不必要条件
B．必要不充分条件
C．充要条件
D．既不充分也不必要条件
【分析】由“”可得直线l与平面α的关系，可解决此题．
【解答】解：由“”可知⊥，可得直线l∥平面α或l⊂α，
∴“”是“l∥α”的必要不充分条件，
故选：B．
【点评】本题考查空间直线与平面及充分、必要条件的判定，考查直观想象能力，属于基础题．
3．（4分）已知圆，圆，那么两圆的位置关系是（ ）
A．相交B．外离C．外切D．内含
【分析】先求出两圆的圆心坐标和半径，进而判断两圆的位置关系．
【解答】解：圆，化为标准方程为x2+（y+3）2＝1，圆心C1（0，﹣3），半径r1＝1，
圆，圆心C2（0，0），半径r2＝3，
∵|C1C2|＝3，
∴r2﹣r1＜|C1C2|＜r1+r2，
∴两圆相交．
故选：A．
【点评】本题主要考查了圆与圆的位置关系，属于基础题．
4．（4分）已知点A（1，2，﹣1），B（2，t，0），O为坐标原点，且，则＝（ ）
A．B．C．D．
【分析】根据，求得t的值，再利用向量的模公式求解即可．
【解答】解：＝（1，2，﹣1），＝（2，t，0），
由，得1×2+2t+（﹣1）×0＝0，解得t＝﹣1，
＝（1，﹣3，1），||＝＝．
故选：D．
【点评】本题考查向量的模的计算，考查向量的数量积的计算，是基础题．
5．（4分）在同一平面直角坐标系中，直线l1：ax+y+b＝0和直线l2：bx+y+a＝0有可能是（ ）
A．B．
C．D．
【分析】把直线l1和直线l2的方程分别化为：l1：y＝﹣ax﹣b，l2：y＝﹣bx﹣a．由方程看到：l1的斜率﹣a与l2的截距相同，l1的截距﹣b与l2的斜率相同．
【解答】解：直线l1：ax+y+b＝0和直线l2：bx+y+a＝0分别化为：l1：y＝﹣ax﹣b，l2：y＝﹣bx﹣a．
由方程看到：l1的斜率﹣a与l2的截距相同，
l1的截距﹣b与l2的斜率相同．
据此可判断出：只有B满足上述条件．
故选：B．
【点评】本题考查了直线的斜率、截距的意义，属于基础题．
6．（4分）已知直线mx+4y﹣2＝0与2x﹣5y+n＝0互相垂直，垂足为P（1，p），则m﹣n+p的值是（ ）
A．24B．20C．0D．﹣4
【分析】先由两直线平行斜率相等，求出m，第一直线的方程确定了，把垂足坐标代入，可求p，垂足坐标确定了．
把垂足坐标代入第二条直线的方程可得 n，进而求得m﹣n+p的值．
【解答】解：∵直线mx+4y﹣2＝0与2x﹣5y+n＝0互相垂直，
∴×＝﹣1，
∴m＝10，
直线mx+4y﹣2＝0 即 5x+2y﹣1＝0，垂足（1，p）代入得，5+2p﹣1＝0，∴p＝﹣2．
把P（1，﹣2）代入2x﹣5y+n＝0，可得 n＝﹣12，
∴m﹣n+p＝20，
故选：B．
【点评】本题考查两直线垂直的性质，垂足是两直线的公共点，垂足坐标同时满足两直线的方程．
7．（4分）若表示焦点在x轴上的椭圆，则实数a的取值范围是（ ）
A．（﹣2，+∞）B．（﹣∞，﹣1）∪（2，+∞）
C．（﹣2，﹣1）∪（2，+∞）D．任意实数R
【分析】根据椭圆的几何性质建立不等式组，即可求解．
【解答】解：∵表示焦点在x轴上的椭圆，
∴a2＞a+2＞0，
解得a∈（﹣2，﹣1）∪（2，+∞）．
故选：C．
【点评】本题考查椭圆的几何性质，不等式思想，属基础题．
8．（4分）在棱长为1的正方体ABCD﹣A1B1C1D1中，点E为棱A1B1的中点，则点E到平面BC1D1的距离为（ ）
A．B．C．D．
【分析】由，利用等体积法求解．
【解答】解：设点E到平面BC1D1的距离为h，
因为，
即，
所以，
故选：B．
【点评】本题主要考查点面距离的计算，属于基础题．
9．（4分）已知直线l1：mx﹣y+m＝0与直线l2：x+my﹣1＝0的交点为Q，椭圆的焦点为F1，F2，则|QF1|+|QF2|的取值范围是（ ）
A．[2，+∞）B．C．[2，4]D．
【分析】判断两条直线经过的定点，判断交点所在的位置利用椭圆的定义判断求解即可．
【解答】解：椭圆的焦点为F1（﹣，0），F2（，0）；
直线l1：mx﹣y+m＝0与直线l2：x+my﹣1＝0的交点为Q，两条直线经过定点（﹣1，0），（1，0），
它们的交点Q满足：x2+y2＝1，在椭圆内部，与椭圆的短轴端点相交，
所以|QF1|+|QF2|的取值范围是：[2，4]．
故选：D．
【点评】本题考查椭圆的简单性质的应用，轨迹方程的求法，考查计算能力．
10．（4分）如图，正方体ABCD﹣A1B1C1D1中，N为CD1中点，M为线段BC1上的动点（M不与B，C1重合），以下四个命题：
（1）CD1⊥平面BMN；
（2）MN∥平面AB1D1；
（3）△D1MN的面积与△CMN的面积相等；
（4）三棱锥D﹣MNC的体积有最大值
其中真命题的个数为（ ）
A．1B．2C．3D．4
【分析】直接利用空间中线线关系，线面关系及面面关系逐一判断4个命题得答案．
【解答】解：（1）CD1与BM不垂直，所以CD1⊥平面BMN，不正确；
（2）平面BMN∥平面AB1D1，所以MN∥平面AB1D1，正确；
（3）两个三角形等底等高，△D1MN的面积与△CMN的面积相等，正确；
（4）M与B重合，三棱锥D﹣MNC的体积最大，不正确．
故选：B．
【点评】本题考查了命题的真假判断与应用，考查了空间中的线线关系和线面关系，考查了学生的空间想象能力和思维能力，是中档题．
二、填空题（本题共5道小题，每小题5分，共25分）
11．（5分）椭圆4x2+9y2＝36的焦点坐标为 （，0） ，若P为椭圆上任意一点，F1，F2为椭圆的左右焦点，则|PF1|+|PF2|＝ 6 ．
【分析】根据椭圆的几何性质即可求解．
【解答】解：∵椭圆方程4x2+9y2＝36可化为，
∴a＝3，b＝2，c＝，且焦点在x轴上，
∴焦点坐标为（，0）；
∵P为椭圆上任意一点，
∴|PF1|+|PF2|＝2a＝6．
故答案为：（，0）；6．
【点评】本题考查椭圆的几何性质，属基础题．
12．（5分）过椭圆+＝1（a＞b＞0）的左焦点F1作x轴的垂线交椭圆于点P，F2为右焦点，若∠F1PF2＝60°，则椭圆的离心率为 ．
【分析】把x＝﹣c代入椭圆方程求得P的坐标，进而根据∠F1PF2＝60°推断出 ＝整理得 e2+2e﹣＝0，进而求得椭圆的离心率e．
【解答】解：由题意知点P的坐标为（﹣c，）或（﹣c，﹣），
∵∠F1PF2＝60°，
∴＝，
即2ac＝b2＝（a2﹣c2）．
∴e2+2e﹣＝0，
∴e＝或e＝﹣（舍去）．
故答案为：．
【点评】本题主要考查了椭圆的简单性质，考查了考生综合运用椭圆的基础知识和分析推理的能力，属基础题．
13．（5分）能说明“直线x﹣y+m＝0与圆x2+y2+4x﹣2y＝0有两个不同的交点”是真命题的一个m的值为 0 ．
【分析】把圆的方程整理为标准方程，找出圆心坐标与半径r，根据直线与圆有两个不同交点得到直线与圆相交，即圆心到直线的距离d小于半径r，求出m的范围，即可作出判断．
【解答】解：圆方程整理得：（x+2）2+（y﹣1）2＝5，
∴圆心（﹣2，1），半径r＝，
∵直线x﹣y+m＝0与圆x2+y2+4x﹣2y＝0有两个不同交点，
∴直线与圆相交，即d＜r，
∴＜，即|m﹣3|＜，
解得：﹣+3＜m＜+3，
故能说明“直线x﹣y+m＝0与圆x2+y2+4x﹣2y＝0有两个不同的交点”是真命题的一个m的值可以为0．
故答案为0．
【点评】此题考查了直线与圆相交的性质，直线与圆有两个不同的交点即为直线与圆相交．
14．（5分）已知圆C过点A（﹣1，2），B（1，0），则圆心C到原点距离的最小值为 ．
【分析】由圆的性质可得圆心在弦的中垂线上，由题意可得圆心所在的直线的方程，原点到圆心的最小距离及为原点到圆心所在的直线的距离，求出其值．
【解答】解：由题意可得圆心在AB所在的中垂线上，因为A（﹣1，2），B（1，0），AB的中点D（0，1），
因为kAB＝＝﹣1，所以AB的中垂线的斜率为k＝1，
所以中垂线的方程为y＝x+1，即x﹣y+1＝0，
所以圆心C到原点距离的最小值为O到直线x﹣y+1＝0的距离d＝＝，
故答案为：．
【点评】本题考查圆的性质的应用及点到直线的距离公式的应用，属于基础题．
15．（5分）数学中有许多寓意美好的曲线，曲线C：（x2+y2）3＝4x2y2被称为“四叶玫瑰线”（如图所示）．给出下列三个结论：
①曲线C关于直线y＝x对称；
②曲线C上任意一点到原点的距离都不超过1；
③存在一个以原点为中心、边长为的正方形，使得曲线C在此正方形区域内（含边界）．
其中，正确结论的序号是 ①② ．
【分析】根据曲线的方程以及图象逐个判断3个结论即可得出．
【解答】解：对①，用（y，x）替换方程中的（x，y），方程形式不变，所以曲线C关于直线y＝x对称，正确；
对②，设点P（x，y）是曲线上任意一点，则（x2+y2）3＝4x2y2，则点P到原点的距离为，
由（x2+y2）3＝4x2y2≤4×，解得≤1，正确；
对③，由②可知，包含该曲线的以原点为圆心的最小的圆的半径为1，
所以最小圆应该是包含该曲线的最小正方形的内切圆，
即正方形的边长最短为2，所以不正确；
故答案为：①②．
【点评】本题主要考查函数曲线的性质应用，意在考查学生的直观想象能力和分析能力，属于中档题．
三、解答题（本题共6道小题，共85分.要求有演算或推理步骤）
16．（13分）已知△ABC的顶点坐标分别是A（﹣1，5），B（﹣2，﹣1），C（4，3）．M为BC边的中点．
（Ⅰ）求中线AM的方程；
（Ⅱ）求经过点C且与直线AB平行的直线方程．
【分析】（Ⅰ）先求出中点M的坐标，再结合直线的斜率公式，即可求解；
（Ⅱ）根据已知条件，结合直线平行的性质，以及直线的斜率公式，即可求解．
【解答】解：（Ⅰ）B（﹣2，﹣1），C（4，3），M为BC边的中点，
则M（1，1），
A（﹣1，5），
则，
故中线AM的方程为y﹣1＝﹣2（x﹣1），即2x+y﹣3＝0；
（Ⅱ）A（﹣1，5），B（﹣2，﹣1），
则，
故所求直线的斜率为6，
所求直线过点C（4，3），
故所求直线方程为y﹣3＝6（x﹣4），即6x﹣y﹣21＝0．
【点评】本题主要考查直线平行的性质，属于基础题．
17．（13分）如图，在正方体ABCD﹣A1B1C1D1中，E为DD1的中点．
（Ⅰ）求证：BD1∥平面ACE；
（Ⅱ）求直线AD与平面ACE所成角的正弦值．
【分析】（Ⅰ）连接BD交AC于点O，连接OE，证明OE∥BD1.然后证明BD1∥平面ACE．
（Ⅱ）不妨设正方体的棱长为2，建立空间直角坐标系A﹣xyz．求出平面ACE的法向量，利用空间向量的数量积求解直线AD与平面ACE所成角的正弦值即可．
【解答】（Ⅰ）证明：连接BD交AC于点O，连接OE，
在正方形ABCD中，OB＝OD．
因为E为DD1的中点，
所以OE∥BD1.………………（3分）
因为BD1⊄平面ACE，OE⊂平面ACE，
所以BD1∥平面ACE． ………………（5分）
（Ⅱ）解：不妨设正方体的棱长为2，建立如图所示的空间直角坐标系A﹣xyz．
则A（0，0，0），C（2，2，0），D（0，2，0），E（0，2，1），
所以，，． ………………（8分）
设平面ACE的法向量为＝（x，y，z），
所以所以即………………（10分）
令y＝﹣1，则x＝1，z＝2，
于是＝（1，﹣1，2）．………………（11分）
设直线AD与平面ACE所成角为θ，
则．………………（13分）
所以直线AD与平面ACE所成角的正弦值为．
【点评】本题考查直线与平面平行的判定定理的应用，直线与平面所成角的求法，考查空间想象能力，转化思想以及计算能力，是中档题．
18．（14分）求满足下列条件的曲线方程．
（1）求过点A（3，5）且与圆O：x2+y2﹣2x﹣4y+1＝0相切的直线方程；
（2）求圆心在直线3x﹣y＝0上，与x轴相切，且被直线x﹣y＝0截得的弦长为的圆的方程．
【分析】（1）设方程为y﹣5＝k（x+3），由直线与圆相切可得，＝2，可求k，然后检验斜率不存在时的情况，即可得到直线方程．
（2）设出圆的圆心与半径，结合已知条件，转化求解圆的方程．
【解答】解：（1）设方程为y﹣5＝k（x+3），圆（x﹣1）2+（y﹣2）2＝4，圆心坐标是（1，2），半径r＝2，
由直线与圆相切可得，＝2，
∴k＝，
当直线的斜率不存在时，此时直线的方程为x＝3也满足题意，
综上可得，所求的切线方程为x＝3和5x﹣12y+45＝0．
（2）由已知设圆心为（a，3a），与x轴相切则r＝|3a|．
圆心到直线的距离，弦长为，得：7+，解得a＝±1．
圆心为（1，3）或（﹣1，﹣3），r＝3，
所求圆的方程为（x﹣1）2+（y﹣3）2＝9或（x+1）2+（y+3）2＝9．
【点评】本题考查直线与圆的位置关系的应用，直线方程的求法，圆的方程的求法，是中档题．
19．（15分）在三棱锥P﹣ABC中，平面PAC⊥平面ABC，△PAC为等腰直角三角形，PA⊥PC，AC⊥BC，BC＝2AC＝4，M为AB的中点．
（Ⅰ）求证：AC⊥PM；
（Ⅱ）求二面角C﹣PA﹣B的余弦值；
（Ⅲ）在线段PB上是否存在点N使得平面CMN⊥平面PAB？若存在，求出的值，若不存在，说明理由．
【分析】（1）由线面垂直的判定定理即可证明AC⊥平面PMD，从而证得AC⊥PM；
（2）建立空间直角坐标系，由向量法即可求二面角；
（3）设，（0＜λ＜1），由面面垂直的向量表示建立方程即可求得λ．
【解答】证明：（1）如图，设D为AC的中点，连接MD，PD，
因为M为AB的中点，所以MD∥BC，
因为AC⊥BC，所以MD⊥AC，
又△PAC为等腰直角三角形，PA⊥PC，所以PD⊥AC，
因为MD∩PD＝D，MD，PD⊂平面PMD，所以AC⊥平面PMD，
因为PM⊂平面PMD，所以AC⊥PM；
解：（2）由（1）知，可建立以D为坐标原点，，，的方向分别为x轴、y轴、z轴正方向的空间直角坐标系，如图所示，
则A（1，0，0），B（﹣1，4，0），C（﹣1，0，0），P（0，0，1），
所以，0，1），＝（1，﹣4，1），
设平面PAB的法向量为＝（x，y，z），则，
令z＝1，则＝（1，，
由题可知，平面PAC的一个法向量为，
设二面角C﹣PA﹣B的平面角为θ，由图可知，θ为锐角，
所以＝＝，
所以二面角C﹣PA﹣B的余弦值为；
解：（3）存在．理由如下：假设在线段PB上存在点N，使平面CNM⊥平面PAB，
设，（0＜λ＜1），因为＝（﹣1，4，﹣1），所以，4λ，﹣λ），所以N（﹣λ，4λ，1﹣λ），
因为M（0，2，0），C（﹣1，0，0），所以＝（1﹣λ，4λ，1﹣λ），，
设平面CNM的法向量为＝（a，b，c），则，
令b＝1，则，
因为平面CNM⊥平面PAB，所以＝，解得，
所以存在点N使得平面CNM⊥平面PAB，此时．
【点评】本题考查线面垂直的证明，二面角的求法，面面垂直的应用，属与于中档题．
20．（15分）已知椭圆G：，斜率为1的直线l与椭圆G交于A，B两点，以AB为底边作等腰三角形，顶点为P（﹣3，2）．
（Ⅰ）求椭圆G的离心率；
（Ⅱ）求△PAB的面积．
【分析】（Ⅰ）由椭圆的离心率公式直接求解即可；
（Ⅱ）设直线AB的方程为y＝x+b，与椭圆方程联立，表示出AB的中点坐标M，进而表示出AB的中垂线方程，代入点P的坐标，可得b的值，再利用弦长公式和点到直线的距离公式即可得解．
【解答】解：（Ⅰ）由于椭圆G：，
则椭圆G的离心率为；
（Ⅱ）设直线AB的方程为y＝x+b，
代入，得4x2+6bx+3b2﹣12＝0，
由韦达定理可知，，
则，
设M为AB的中点，则，AB的中垂线斜率K＝﹣1．
∴中垂线方程为l：，
将P（﹣3，2）代入，得b＝2，
∴直线AB方程为x﹣y+2＝0，
根据弦长公式可得，
点P到直线AB的距离为，
则．
【点评】本题考查椭圆的标准方程及其性质，考查直线与椭圆的综合运用，考查运算求解能力，属于中档题．
21．（15分）已知椭圆E：+＝1（a＞b＞0）经过点（﹣1，），其离心率e＝．
（Ⅰ）求椭圆E的方程；
（Ⅱ）设动直线l：y＝kx+m与椭圆C相切，切点为T，且l与直线x＝﹣4相交于点S．
试问：在x轴上是否存在一定点，使得以ST为直径的圆恒过该定点？若存在，求出该点的坐标；若不存在，请说明理由．
【分析】（Ⅰ）由题意可知：将点代入椭圆方程，利用椭圆的离心率公式即可求得a和b的值，即可求得椭圆方程；
（Ⅱ）将直线方程代入椭圆方程，由Δ＝0，求得4k2﹣m2+3＝0，利用韦达定理及中点坐标公式，求得T点坐标，联立即可求得S点坐标，由•＝0，根据向量数量积的坐标运算，可得，即可求得A点坐标，即可求得以ST为直径的圆恒过该定点（1，0）．
【解答】解：（Ⅰ）由点（﹣1，）在椭圆上得，代入椭圆方程：，①﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣（1分）
椭圆的离心率e＝＝，则a＝2c，a2＝4c2，b2＝3c2，②﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣（2分）
②代入①解得c2＝1，a2＝4，b2＝3，
故椭圆E的标准方程为；﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣（4分）
（Ⅱ）由，消去y，整理得（4k2+3）x2+8kmx+4m2﹣12＝0；
因为动直线l与椭圆E相切，即它们有且只有一个公共点T，可设T（x0，y0），
m≠0，Δ＝0，∴（8km）2﹣4×（4k2+3）×（4m2﹣12）＝0，
∴4k2﹣m2+3＝0，③﹣﹣﹣﹣（6分）
此时，x0＝＝﹣＝﹣，y0＝kx0+m＝，则T（﹣，）．﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣（7分）
由，得S（﹣4，﹣4k+m）．﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣（8分）
假设平面内存在定点满足条件，不妨设为点A．
由图形对称性知，点A必在x轴上．﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣（9分）
设A（x1，0），则由已知条件知AS⊥AT，
即•＝0对满足③式的m，k恒成立．﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣（10分）
由＝（﹣4﹣x1，﹣4k+m），＝（﹣﹣x1，），由•＝0得：++4x1+x12﹣+3＝0，
整理得（4x1+4）+x12+4x1+3＝0，④﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣（12分）
由④式对满足③式的m，k恒成立，则，解得x1＝﹣1．
故平面内存在定点（﹣1，0），使得以ST为直径的圆恒过该定点．﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣（14分）
【点评】本题考查椭圆的标准方程，直线与椭圆的位置关系，考查韦达定理，中点坐标公式，向量数量积的坐标运算，考查计算能力，属于中档题．
声明：试题解析著作权属菁优网所有，未经书面同意，不得复制发布日期：2024/7/23 9:45:51；用户：菁优校本题库；邮箱：2471@xyh.cm；学号：56380052