2022-2023学年北京市门头沟区大峪中学高二（上）期中数学试卷

这是一份2022-2023学年北京市门头沟区大峪中学高二（上）期中数学试卷，共21页。
A．120°B．150°C．30°D．60°
2．（4分）如图，直线l1，l2，l3，l4的斜率分别为k1，k2，k3，k4，则（ ）
A．k4＜k3＜k2＜k1B．k3＜k4＜k2＜k1
C．k4＜k3＜k1＜k2D．k3＜k4＜k1＜k2
3．（4分）过两直线x+y﹣3＝0，2x﹣y＝0的交点，且与直线平行的直线方程为（ ）
A．x+3y+5＝0B．x+3y﹣5＝0C．x﹣3y+5＝0D．x﹣3y﹣5＝0
4．（4分）已知方程x2+y2+2x﹣y+m＝0表示圆，则实数m的取值范围是（ ）
A．m＞B．m＞﹣C．m＜D．m＜﹣
5．（4分）经过三个点的圆的方程为（ ）
A．B．
C．D．
6．（4分）已知＝（2，3，﹣2），＝（﹣4，2，1），＝（10，3，λ），若、、三个向量共面，则实数λ等于（ ）
A．B．C．D．
7．（4分）已知A（0，0，1），B（3，0，0），C（0，2，0），则原点到平面ABC的距离是（ ）
A．B．C．1D．
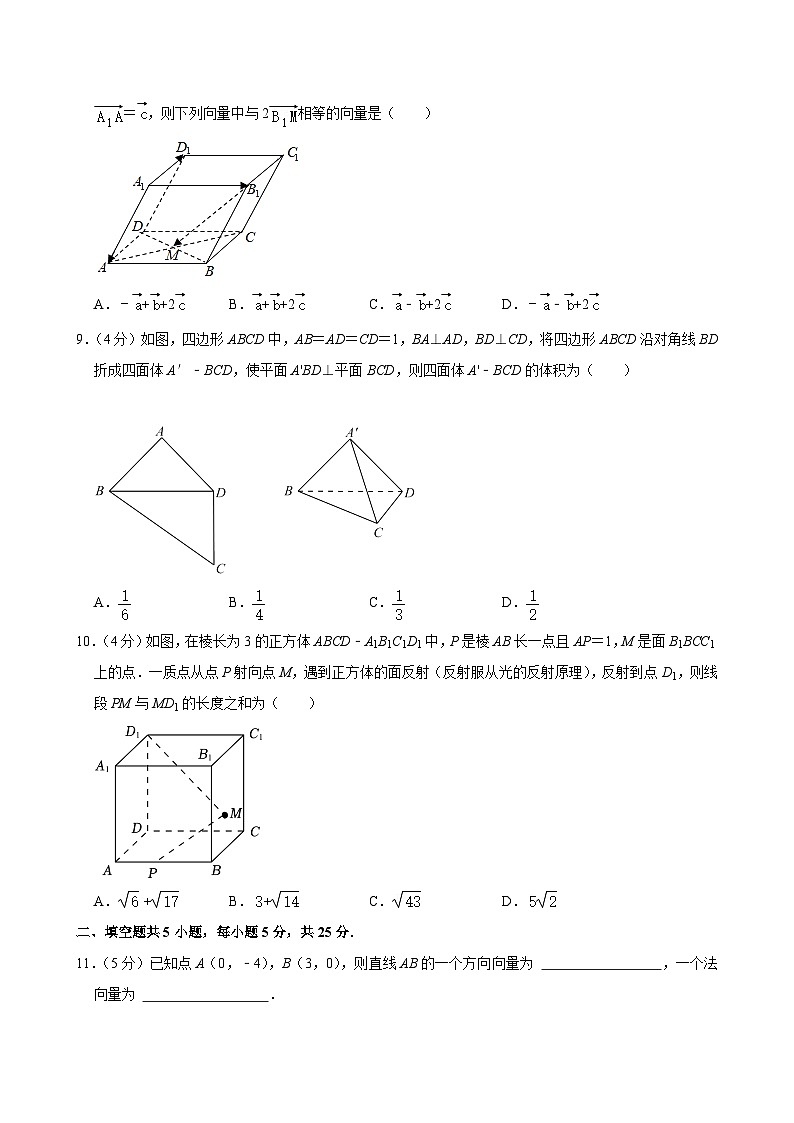
8．（4分）如图，在平行六面体ABCD﹣A1B1C1D1中，AC与BD的交点为M．设＝，＝，＝，则下列向量中与2相等的向量是（ ）
A．﹣++2B．++2C．﹣+2D．﹣﹣+2
9．（4分）如图，四边形ABCD中，AB＝AD＝CD＝1，BA⊥AD，BD⊥CD，将四边形ABCD沿对角线BD折成四面体A′﹣BCD，使平面A'BD⊥平面BCD，则四面体A'﹣BCD的体积为（ ）
A．B．C．D．
10．（4分）如图，在棱长为3的正方体ABCD﹣A1B1C1D1中，P是棱AB长一点且AP＝1，M是面B1BCC1上的点．一质点从点P射向点M，遇到正方体的面反射（反射服从光的反射原理），反射到点D1，则线段PM与MD1的长度之和为（ ）
A．B．C．D．
二、填空题共5小题，每小题5分，共25分．
11．（5分）已知点A（0，﹣4），B（3，0），则直线AB的一个方向向量为 ，一个法向量为 ．
12．（5分）如图，在正方体ABCD﹣A1B1C1D1中，E，F，G，H分别为AA1，AB，BB1，B1C1的中点，则异面直线EF与GH所成的角等于 ．
13．（5分）直线l：ax+y﹣2＝0在x轴和y轴上的截距相等，则a＝ ．
14．（5分）过圆x2+y2﹣2x+4y﹣4＝0内一点M（3，0）作圆的割线l，使它被该圆截得的线段最短，则直线l的方程是 ．
15．（5分）在平面直角坐标系中，定义d（P，Q）＝|x1﹣x2|+|y1﹣y2|为两点P（x1，y1），Q（x2，y2）之间的“折线距离“：在这个定义下，给出下列命题：
①到原点的“折线距离”等于1的点的集合是一个圆；
②到原点的“折线距离”等于1的点的集合是一个正方形；
③到M（﹣1，0），N（1，0）两点的“折线距离”差的绝对值为1的点的集合是两条平行线；
④到M（﹣1，0），N（1，0）两点的“折线距离”之和为6的点的集合是面积为16的六边形．
其中正确的命题是 .（写出所有正确命题的序号）
三、解答题共6小题，共85分．解答应写出文字说明，演算步骤或证明过程．
16．（12分）已知平行四边形ABCD的三个顶点的坐标为A（﹣1，4），B（﹣2，﹣1），C（2，3）．
（1）在△ABC中，求边AC中线所在直线方程；
（2）求平行四边形ABCD的顶点D的坐标及边BC的长度．
17．（13分）已知直线l1：ax﹣2y+3＝0，l2：x+（a﹣3）y+5a＝0．
（Ⅰ）当a＝1时，求两直线的距离；
（Ⅱ）若l1⊥l2，求a的值；
（Ⅲ）写出原点到直线l1的距离，并求出该距离的最大值．
18．（15分）已知两点D（4，2），M（3，0）及圆C：（x﹣2）2+（y﹣3）2＝5，l为经过点M的一条动直线．
（1）若直线l经过点D，求证：直线l与圆C相切；
（2）若直线l与圆C相交于两点A，B，从下列条件中选择一个作为已知条件，并求△ABD的面积．
条件①：直线l平分圆C；条件②：直线l的斜率为﹣3．
19．（15分）如图，在三棱柱ABC﹣A1B1C1中，BB1⊥平面ABC，△ABC为正三角形，侧面ABB1A1是边长为2的正方形，D为BC的中点．
（Ⅰ）求证：平面ADC1⊥平面BCC1B1；
（Ⅱ）求二面角C﹣AB﹣C1大小的余弦值．
20．（15分）在四棱锥P﹣ABCD中，底面ABCD是矩形，侧棱PA⊥底面ABCD，E，F分别是AB，PC的中点，PA＝AD＝2，．
（1）求证：EF∥平面PAD；
（2）求PC与平面DEF所成角的正弦值；
（3）在棱BC上是否存在一点M，使得DE⊥平面PAM？若存在．求出的值；若不存在，请说明理由．
21．（15分）已知直线l1，l2均过点P（1，2）．
（Ⅰ）若直线l1过点A（﹣1，3），且l1⊥l2，求直线l2的方程；
（Ⅱ）如图，O为坐标原点，若直线l1的斜率为k，其中0＜k≤2，且与y轴交于点N，直线l2过点，且与x轴交于点M，求直线l1，l2与两坐标轴围成的四边形PNOM面积的最小值．
2022-2023学年北京市门头沟区大峪中学高二（上）期中数学试卷
参考答案与试题解析
一、选择题共10小题，每小题4分，共40分．在每小题四个选项中，选出符合题目要求的一项．
1．（4分）直线x﹣y﹣1＝0的倾斜角是（ ）
A．120°B．150°C．30°D．60°
【分析】根据直线和斜率和倾斜角的关系即可求出．
【解答】解：直线的倾斜角为θ，
则tanθ＝，
∴θ＝60°，
故选：D．
【点评】本题考查了直线和斜率和倾斜角的关系，属于基础题
2．（4分）如图，直线l1，l2，l3，l4的斜率分别为k1，k2，k3，k4，则（ ）
A．k4＜k3＜k2＜k1B．k3＜k4＜k2＜k1
C．k4＜k3＜k1＜k2D．k3＜k4＜k1＜k2
【分析】根据直线的斜率与倾斜角的关系，即可得解．
【解答】解：由k＝tanα知，当倾斜角α在这一变化时，直线的斜率k逐渐增大，所以0＜k1＜k2，
当倾斜角α在第二象限变化时，直线的斜率k逐渐增大，所以k3＜k4＜0，
所以k3＜k4＜k1＜k2．
故选：D．
【点评】本题考查直线的斜率与倾斜角的关系，熟练掌握正切函数的图象与性质是解题的关键，属于基础题．
3．（4分）过两直线x+y﹣3＝0，2x﹣y＝0的交点，且与直线平行的直线方程为（ ）
A．x+3y+5＝0B．x+3y﹣5＝0C．x﹣3y+5＝0D．x﹣3y﹣5＝0
【分析】先联立两直线方程，求出两直线的交点坐标，依题意可设所求直线方程为y＝+k（k≠0），代入交点坐标，即可求出k的值，从而得到直线方程．
【解答】解：联立方程，解得：，
∴直线x+y﹣3＝0，2x﹣y＝0的交点坐标为（1，2），
设所求直线方程为y＝+k（k≠0），
代入点（1，2）得，2＝，
∴k＝，
∴所求直线方程为y＝+，即x﹣3y+5＝0，
故选：C．
【点评】本题主要考查了直线的一般方程，考查了两直线平行的位置关系，是基础题．
4．（4分）已知方程x2+y2+2x﹣y+m＝0表示圆，则实数m的取值范围是（ ）
A．m＞B．m＞﹣C．m＜D．m＜﹣
【分析】由圆的一般式方程可得D2+E2﹣4F＞0，即 4+1﹣4m＞0，由此求得m的范围．
【解答】解：由圆的一般式方程可得D2+E2﹣4F＞0，即 4+1﹣4m＞0，求得 m＜，
故选：C．
【点评】本题主要考查圆的一般式方程的特征，属于基础题．
5．（4分）经过三个点的圆的方程为（ ）
A．B．
C．D．
【分析】利用待定系数法设出圆的方程，代入点的坐标求解即可．
【解答】解：因为圆经过三个点，
设圆的方程为（x﹣a）2+（y﹣b）2＝r2，
则，解得 ，
所以圆的方程为．
故选：C．
【点评】本题考查了圆的方程的求解，主要考查了待定系数法的应用，考查了逻辑推理能力与化简运算能力，属于基础题．
6．（4分）已知＝（2，3，﹣2），＝（﹣4，2，1），＝（10，3，λ），若、、三个向量共面，则实数λ等于（ ）
A．B．C．D．
【分析】由、、三个向量共面，得＝x+y（x≠0，y≠0），列方程组，能求出结果．
【解答】解：∵＝（2，3，﹣2），＝（﹣4，2，1），＝（10，3，λ），若、、三个向量共面，
∴＝x+y（x≠0，y≠0），
∴（2，3，﹣2）＝（﹣4x，2x，x）+（10y，3y，λy）＝（﹣4x+10y，2x+3y，x+λy），
∴，
解得x＝，y＝，
∴实数λ＝﹣．
故选：D．
【点评】本题考查向量共面定理，考查运算求解能力，属于基础题．
7．（4分）已知A（0，0，1），B（3，0，0），C（0，2，0），则原点到平面ABC的距离是（ ）
A．B．C．1D．
【分析】＝（3，0，﹣1），＝（0，2，﹣1），＝（0，0，﹣1），求出平面ABC的法向量，利用原点到平面ABC的距离是d＝，能求出结果．
【解答】解：A（0，0，1），B（3，0，0），C（0，2，0），
∴＝（3，0，﹣1），＝（0，2，﹣1），＝（0，0，﹣1），
设平面ABC的法向量＝（x，y，z），
则，取x＝2，得＝（2，3，6），
∴原点到平面ABC的距离是：
d＝＝＝．
故选：B．
【点评】本题用到的知识点为：平面的法向量、点到平面的距离公式，考查运算求解能力，是中档题．
8．（4分）如图，在平行六面体ABCD﹣A1B1C1D1中，AC与BD的交点为M．设＝，＝，＝，则下列向量中与2相等的向量是（ ）
A．﹣++2B．++2C．﹣+2D．﹣﹣+2
【分析】在平行六面体ABCD﹣A1B1C1D1中，根据空间向量的加法合成法则，对向量进行线性表示即可．
【解答】解：由题意得，平行六面体ABCD﹣A1B1C1D1中，
2＝2（+）＝2（+）＝2++＝2﹣+＝﹣++2；
故选：A．
【点评】本题考查了空间向量的加法运算问题，解题时应结合图形进行解答，属于基础题．
9．（4分）如图，四边形ABCD中，AB＝AD＝CD＝1，BA⊥AD，BD⊥CD，将四边形ABCD沿对角线BD折成四面体A′﹣BCD，使平面A'BD⊥平面BCD，则四面体A'﹣BCD的体积为（ ）
A．B．C．D．
【分析】利用面面垂直的性质定理证明CD⊥平面A'BD，然后由等体积法VA'﹣BCD＝VC﹣A'BD，结合锥体的体积公式求解即可．
【解答】解：由题意，平面A'BD⊥平面BCD，平面A'BD∩平面BCD＝BD，又BD⊥CD，CD⊂平面BCD，
则CD⊥平面A'BD，
因为AB＝AD＝CD＝1，
所以，
则由等体积法可得，VA'﹣BCD＝VC﹣A'BD＝＝，
所以四面体A'﹣BCD的体积为．
故选：A．
【点评】本题考查了空间中的翻折问题，面面垂直的性质定理的应用，棱锥体积的求解，要注意翻折前后不变的信息，对于三棱锥的体积问题，一般会运用等体积法求解，考查了逻辑推理能力与化简运算能力，属于中档题．
10．（4分）如图，在棱长为3的正方体ABCD﹣A1B1C1D1中，P是棱AB长一点且AP＝1，M是面B1BCC1上的点．一质点从点P射向点M，遇到正方体的面反射（反射服从光的反射原理），反射到点D1，则线段PM与MD1的长度之和为（ ）
A．B．C．D．
【分析】以点D为坐标原点，DA、DC、DD1所在直线分别为x、y、z轴建立空间直角坐标系，作点P关于平面BCC1B1的对称点Q，计算出|D1Q|即可．
【解答】解：以点D为坐标原点，DA、DC、DD1所在直线分别为x、y、z轴建立如图所示的空间直角坐标系，
则D1（0，0，3）、P（3，1，0），
作点P关于平面BCC1B1的对称点Q（3，5，0），由对称性可知|PM|＝|MQ|，
且D1、M、Q三点共线，
故|PM|+|MD1|＝|QM|+|MD1|＝＝．
故选：C．
【点评】本题主要考查空间中的距离，属于基础题．
二、填空题共5小题，每小题5分，共25分．
11．（5分）已知点A（0，﹣4），B（3，0），则直线AB的一个方向向量为 （3，4）（不唯一） ，一个法向量为 （4，﹣3）（不唯一） ．
【分析】直接由方向向量以及法向量的定义求解即可．
【解答】解：由题意知，直线AB的一个方向向量为，
则直线的法向量与方向向量垂直，故数量积为0，可选取一个法向量为（4，﹣3）．
故答案为：（3，4）（不唯一）；（4，﹣3）（不唯一）．
【点评】本题主要考查方向向量、法向量的定义，属于基础题．
12．（5分）如图，在正方体ABCD﹣A1B1C1D1中，E，F，G，H分别为AA1，AB，BB1，B1C1的中点，则异面直线EF与GH所成的角等于 60° ．
【分析】利用异面直线夹角的定义，将EF平移至MG（G为A1B1中点），通过△MGH为正三角形求解．
【解答】解：取A1B1 中点M连接MG，MH，则MG∥EF，MG与GH所成的角等于EF与GH所成的角．容易知道△MGH为正三角形，∠MGH＝60°
∴EF与GH所成的角等于60°
故答案为：60°
【点评】本题考查异面直线夹角的计算，利用定义转化成平面角，是基本解法．找平行线是解决问题的一个重要技巧，一般的“遇到中点找中点，平行线即可出现”．
13．（5分）直线l：ax+y﹣2＝0在x轴和y轴上的截距相等，则a＝ 1 ．
【分析】把直线l：ax+y﹣2＝0化为截距式：．利用截距相等即可得出．
【解答】解：把直线l：ax+y﹣2＝0化为．
∵直线l：ax+y﹣2＝0在x轴和y轴上的截距相等，
∴，解得a＝1．
故答案为：1．
【点评】本题考查了直线的截距式，属于基础题．
14．（5分）过圆x2+y2﹣2x+4y﹣4＝0内一点M（3，0）作圆的割线l，使它被该圆截得的线段最短，则直线l的方程是 x+y﹣3＝0 ．
【分析】将圆的方程化为标准方程，找出圆心A的坐标，由垂径定理得到与直径AM垂直的弦最短，根据A和M的坐标求出直线AM的斜率，利用两直线垂直时斜率的乘积为﹣1，求出直线l的斜率，由求出的斜率及M的坐标，即可得到直线l的方程．
【解答】解：将圆的方程化为标准方程得：（x﹣1）2+（y+2）2＝9，
∴圆心A坐标为（1，﹣2），又M（3，0），
∵直线AM的斜率为＝1，
∴直线l的斜率为﹣1，
则直线l的方程为y＝﹣（x﹣3），即x+y﹣3＝0．
故答案为：x+y﹣3＝0．
【点评】此题考查了直线与圆相交的性质，涉及的知识有：圆的标准方程，两直线垂直时斜率满足的关系，以及直线的点斜式方程，根据垂径定理得到与直径AM垂直的弦最短是解本题的关键．
15．（5分）在平面直角坐标系中，定义d（P，Q）＝|x1﹣x2|+|y1﹣y2|为两点P（x1，y1），Q（x2，y2）之间的“折线距离“：在这个定义下，给出下列命题：
①到原点的“折线距离”等于1的点的集合是一个圆；
②到原点的“折线距离”等于1的点的集合是一个正方形；
③到M（﹣1，0），N（1，0）两点的“折线距离”差的绝对值为1的点的集合是两条平行线；
④到M（﹣1，0），N（1，0）两点的“折线距离”之和为6的点的集合是面积为16的六边形．
其中正确的命题是 ②③④ .（写出所有正确命题的序号）
【分析】先根据折线距离的定义分别表示出所求的集合，然后根据集合中绝对值的性质进行判定即可．
【解答】解：到原点的“折线距离”等于1的点的集合{（x，y）||x|+|y|＝1}，是一个正方形，故①错误，②正确；
到M（﹣1，0），N（1，0）两点的“折线距离”差的绝对值为1的点的集合{（x，y）||x+1|+|y|﹣|x﹣1|﹣|y|＝±1}＝{（x，y）||x+1|﹣|x﹣1|＝±1}，化简得x＝±（﹣1＜x＜1），故集合是两条平行线；故③正确，
到M（﹣1，0），N（1，0）两点的“折线距离”之和为6的点的集合是{（x，y）||x+1|+|y|+|x﹣1|+|y|＝6}，故集合是面积为16的六边形，则④正确；
故答案为：②③④．
【点评】本题考查点的轨迹问题，考查了“折线距离”的定义，以及分析问题解决问题的能力，信息给予题首先要理解清楚所给的信息的含义．
三、解答题共6小题，共85分．解答应写出文字说明，演算步骤或证明过程．
16．（12分）已知平行四边形ABCD的三个顶点的坐标为A（﹣1，4），B（﹣2，﹣1），C（2，3）．
（1）在△ABC中，求边AC中线所在直线方程；
（2）求平行四边形ABCD的顶点D的坐标及边BC的长度．
【分析】（1）由题意，利用中点公式求出AC的中点坐标，再用两点式求边AC中线所在直线的方程．
（2）由＝ 求得点D的坐标，利用两点间的距离公式求出|BC|．
【解答】解：（1）平行四边形ABCD的三个顶点的坐标为A（﹣1，4），B（﹣2，﹣1），C（2，3），
由于线段AC的中点为E（，），
故边AC中线所在直线BE的方程为＝，即9x﹣5y+13＝0．
（2）设点D（m，n），
则由＝，可得（m+1，n﹣4）＝（4，4），∴m＝3，n＝8，即点D（3，8），
|BC|＝＝4．
【点评】本题主要考查中点公式，用两点式求直线的方程，向量相等以及两点间的距离公式，属于基础题．
17．（13分）已知直线l1：ax﹣2y+3＝0，l2：x+（a﹣3）y+5a＝0．
（Ⅰ）当a＝1时，求两直线的距离；
（Ⅱ）若l1⊥l2，求a的值；
（Ⅲ）写出原点到直线l1的距离，并求出该距离的最大值．
【分析】（Ⅰ）利用两平行线间的距离公式求解．
（Ⅱ）利用两直线垂直时的斜率关系求解．
（Ⅲ）先利用点到直线距离公式求出原点到直线l1的距离d，再分析d的最小值即可．
【解答】解：（Ⅰ）当a＝1时，直线l1：x﹣2y+3＝0，直线l2：x﹣2y+5＝0，
∴两直线的距离为＝．
（Ⅱ）若l1⊥l2，则a×1+（﹣2）×（a﹣3）＝0，
解得：a＝6，
即a的值为6．
（Ⅲ）原点到直线l1的距离d＝＝，
∴当a＝0时，d的值最大，最大值为．
【点评】本题主要考查了两平行线间的距离，考查了两直线垂直的位置关系，同时考查了点到直线距离公式，属于基础题．
18．（15分）已知两点D（4，2），M（3，0）及圆C：（x﹣2）2+（y﹣3）2＝5，l为经过点M的一条动直线．
（1）若直线l经过点D，求证：直线l与圆C相切；
（2）若直线l与圆C相交于两点A，B，从下列条件中选择一个作为已知条件，并求△ABD的面积．
条件①：直线l平分圆C；条件②：直线l的斜率为﹣3．
【分析】（1）方法一：求出直线l的方程，利用点到直线距离公式求出圆心到直线l的距离，与半径比较得到结论；
方法二：观察到点D在圆C上，求出直线l的斜率及直线CD的斜率，得到直线l与直线CD垂直，从而证明出相切；
（2）选择①：得到直线l过圆心C（2，3），求出直线l的方程，得到D到直线l的距离及AB的长，从而求出面积；
选择②：求出直线l的方程，观察到圆心C（2，3）在直线l上，得到D到直线l的距离及AB的长，从而求出面积．
【解答】（1）证明：方法一：若直线l经过点D，则直线l的方程为，即2x﹣y﹣6＝0．
由题意，圆C的圆心为C（2，3），半径，则圆心C（2，3）到直线l的距离为，
所以直线l与圆C相切．
方法二：由D（4，2）满足C：（x﹣2）2+（y﹣3）2＝5，可知点D在圆C上，圆心为C（2，3）．
若直线l经过点D，则直线l的斜率，
又，所以kl•kCD＝﹣1，所以l⊥CD，
所以直线l与圆C相切．
（2）解：选择条件①：若直线l平分圆C，
则直线l过圆心C（2，3），直线l的方程为，即3x+y﹣9＝0.，
点D（4，2）到直线l的距离，
所以．
选择条件②：若直线l的斜率为﹣3，
则直线l的方程为y﹣0＝﹣3（x﹣3），即3x+y﹣9＝0，
此时圆心C（2，3）在直线l上，则，
点D（4，2）到直线l的距离，
所以．
【点评】本题主要考查直线与圆的位置关系，考查运算求解能力，属于中档题．
19．（15分）如图，在三棱柱ABC﹣A1B1C1中，BB1⊥平面ABC，△ABC为正三角形，侧面ABB1A1是边长为2的正方形，D为BC的中点．
（Ⅰ）求证：平面ADC1⊥平面BCC1B1；
（Ⅱ）求二面角C﹣AB﹣C1大小的余弦值．
【分析】（I）利用BB1⊥平面ABC，得到BB1⊥AD，又AD⊥CB，可证AD⊥面BCC1B1，再证平面ADC1⊥平面BCC1B1．
（II）选作出二面角的平面角∠CEC1，再求其余弦值．
【解答】（I）证明：∵△ABC为正三角形，D为BC的中点．
∴AD⊥CB，
∵BB1⊥平面ABC，AD⊂面ABC，BB1⊥AD，
∵BB1∩AB＝B，
∴AD⊥面BCC1B1，又∵AD⊂面ADC1，
∴平面ADC1⊥平面BCC1B1
（Ⅱ）解：取BA的中点E，连接CE，C1E，∵△ABC为正三角形，∴CE⊥AB，
∵BB1⊥平面ABC，又BB1∥CC1，∴CC1⊥平面ABC，∴∠CEC1为二面角C﹣AB﹣C1平面角，
∵侧面ABB1A1是边长为2的正方形，所以CC1＝2，
∵△ABC为正三角形，∴CE＝，
所以C1E＝，
cs∠CEC1＝＝，
∴二面角C﹣AB﹣C1大小的余弦值为＝．
【点评】本题考查面面垂直的证明方法和用定义法求二面角的大小，属基础题．
20．（15分）在四棱锥P﹣ABCD中，底面ABCD是矩形，侧棱PA⊥底面ABCD，E，F分别是AB，PC的中点，PA＝AD＝2，．
（1）求证：EF∥平面PAD；
（2）求PC与平面DEF所成角的正弦值；
（3）在棱BC上是否存在一点M，使得DE⊥平面PAM？若存在．求出的值；若不存在，请说明理由．
【分析】（1）取PD的中点G，连接AG，FG，则FG∥CD，，证明出四边形AEFG是平行四边形，从而EF∥AG，进而得出EF∥平面PAD；
（2）由PA⊥底面ABCD，则PA⊥AB，PA⊥AD，建立如图所示的空间直角坐标系A﹣xyz，利用法向量求PC与平面DEF所成角的正弦值；
（3）侧棱PA⊥底面ABCD，只要在BC上找到一点M，使得DE⊥AM，即可证明DE⊥平面PAM，根据第（2）问的向量坐标表示，利用向量的数量积为0，求出M坐标，进而得出的值．
【解答】解：（1）
取PD的中点G，连接AG，FG，∵F，G分别是PC，PD的中点，∴FG∥CD，，
∵底面ABCD是矩形，E是AB的中点，
∴AE∥FG，AE＝FG，∴四边形AEFG是平行四边形，
∴EF∥AG，
又∵FE⊄平面PAD，AG⊂平面PAD，∴EF∥平面PAD．
（2）∵PA⊥底面ABCD，∴PA⊥AB，PA⊥AD，
又∵底面ABCD是矩形，∴AB⊥AD，
建立如图所示的空间直角坐标系A﹣xyz，
∴，，D（0，2，0），P（0，0，2），，
∴，，
设平面DEF的法向量，则，即，
令y＝1，得，z＝﹣1，
∴，又，
设PC与平面DEF所成角为θ，
∴，
∴PC与平面DEF所成角的正弦值为．
（3）
∵侧棱PA⊥底面ABCD，
∴只要在BC上找到一点M，使得DE⊥AM，即可证明DE⊥平面PAM，
设BC上存在一点M，则，t∈[0，2]，
∴，∵，
∴由，解得，
∴BC上存在一点M，使得DE⊥平面PAM，
∴．
【点评】本题主要考查了线面平行的判定，线面角的求解，还考查了线面垂直关系的转化，属于中档题．
21．（15分）已知直线l1，l2均过点P（1，2）．
（Ⅰ）若直线l1过点A（﹣1，3），且l1⊥l2，求直线l2的方程；
（Ⅱ）如图，O为坐标原点，若直线l1的斜率为k，其中0＜k≤2，且与y轴交于点N，直线l2过点，且与x轴交于点M，求直线l1，l2与两坐标轴围成的四边形PNOM面积的最小值．
【分析】（Ⅰ）根题意写出直线l1的方程，进而可得直线l1的斜率为﹣，由l1⊥l2，解得k2＝2，进而可得直线l2的方程．
（Ⅱ）根据题意可得直线l1的方程为y﹣2＝k（x﹣1），写出N点的坐标，设直线l1与x轴的交点为T，同样可得T点坐标，M点坐标，则SPNOM＝S△TPM﹣S△TNO＝R2﹣+2，0＜k≤2，即可得出答案．
【解答】解：（Ⅰ）因为直线l1过点P（1，2），A（﹣1，3），
所以直线l1的方程为y﹣2＝（x﹣1），即x+2y﹣5＝0，
所以直线l1的斜率为﹣，
因为l1⊥l2，
所以（﹣）•k2＝﹣1，
所以k2＝2，
所以直线l2的方程为y﹣2＝2（x﹣1），即y＝2x．
（Ⅱ）根据题意可得直线l1的方程为y﹣2＝k（x﹣1），
令x＝0，得y＝2﹣k，即N（0，2﹣k），
令y＝0，得x＝﹣+1，
设直线l1与x轴的交点为T（﹣+1，0），
因为直线l2过P（1，2），Q（0，+2），
所以直线l2的方程为y﹣2＝（x﹣1），即y﹣2＝﹣（x﹣1），
令y＝0，得x＝R2+1，即M（R2+1，0），
所以SPNOM＝S△TPM﹣S△TNO＝[R2+1﹣（﹣+1）]×2﹣×（﹣1）×（2﹣k），
＝R2+﹣＝R2+＝R2﹣+2，0＜k≤2，
当k＝2时，SPNOM最小值为R2+1．
【点评】本题考查直线与直线的位置关系，解题中需要一定的计算能力，属于中档题．
声明：试题解析著作权属菁优网所有，未经书面同意，不得复制发布日期：2024/7/23 9:47:55；用户：菁优校本题库；邮箱：2471@xyh.cm；学号：56380052