

2023-2024学年北京市育才学校高二(上)期中数学试卷
展开
这是一份2023-2024学年北京市育才学校高二(上)期中数学试卷,共16页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
1.(4分)直线y=﹣x+2的倾斜角为( )
A.45°B.60°C.120°D.135°
2.(4分)已知向量,,则=( )
A.B.14C.D.
3.(4分)两个不同的平面α和β,平面α的一个法向量为,平面β的一个法向量,则平面α与平面β( )
A.平行B.垂直C.相交D.不能确定
4.(4分)已知圆M:x2+y2=1与圆N:(x﹣2)2+y2=9,则两圆的位置关系是( )
A.相交B.相离C.内切D.外切
5.(4分)若图中的直线l1、l2、l3的斜率分别为k1、k2、k3,则( )
A.k1<k2<k3B.k2<k1<k3C.k2<k3<k1D.k1<k3<k2
6.(4分)已知椭圆上一点P到椭圆一个焦点的距离为4,则它到另一个焦点的距离( )
A.6B.5C.4D.2
7.(4分)“a=1”是“直线l1:ax+y+2=0与直线l2:x+ay+2=0平行”的( )
A.充要条件
B.充分不必要条件
C.必要不充分条件
D.既不充分也不必要条件
8.(4分)已知半径为1的圆经过点(3,4),则其圆心到原点的距离的最小值为( )
A.4B.5C.6D.7
9.(4分)过点A(1,2)且与原点距离最大的直线方程为( )
A.2x+y﹣4=0B.x+2y﹣5=0C.x+3y﹣7=0D.3x+y﹣5=0
10.(4分)已知MN是正方体内切球的一条直径,点P在正方体表面上运动,正方体的棱长是2,则的取值范围为( )
A.[0,4]B.[0,2]C.[1,4]D.[1,2]
二、填空题(共5小题,每小题5分,共25分.)
11.(5分)圆x2+y2+2y=1的圆心坐标为 ,半径为 .
12.(5分)一个椭圆的长轴长是短轴长的2倍,则该椭圆的离心率为 .
13.(5分)已知点P(x,y)在直线x+y﹣4=0上,O是原点,则OP的最小值是 .
14.(5分)试给出一组试两条直线l1:2x﹣y=0与l2:ax+by﹣3=0互相垂直的实数a,b的值 .
15.(5分)已知M为椭圆上一点,N为椭圆长轴上一点,O为坐标原点.给出下列结论:
①存在点M,N,使得△OMN为等边三角形;
②不存在点M,N,使得△OMN为等边三角形;
③存在点M,N,使得∠OMN=90°;
④不存在点M,N,使得∠OMN=90°.
其中,所有正确结论的序号是 .
三、解答题(共6小题,共85分.解答应写出文字说明,演算步骤或证明过程.)
16.(12分)已知△ABC的顶点坐标为A(﹣1,5)、B(﹣2,﹣1)、C(4,3).
(1)求BC边的中线长;
(2)求AB边的高线所在直线方程.
17.(14分)求下列各圆的标准方程:
(1)圆心在直线y=﹣x上且过M(2,0)、N(0,﹣4)两点的圆的方程;
(2)经过A(﹣1,﹣1)、B(﹣8,0)、C(0,6)三点的圆的方程.
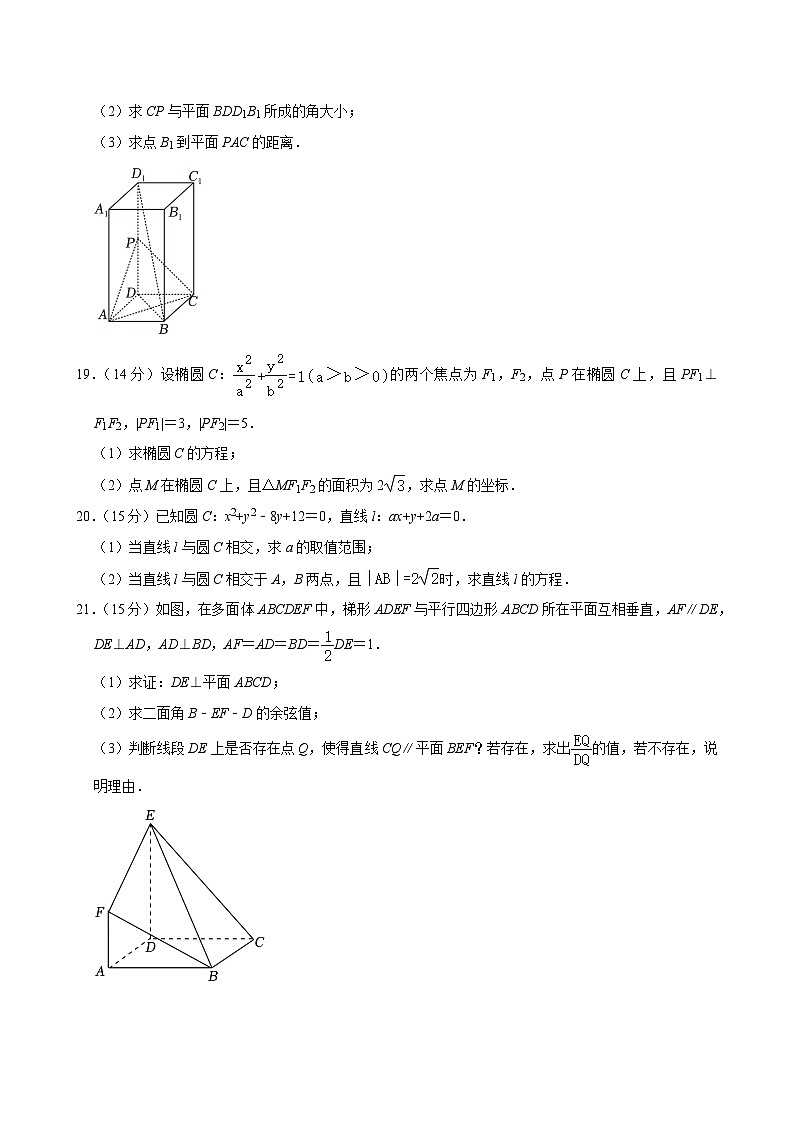
18.(15分)如图,长方体ABCD﹣A1B1C1D1中,AB=AD=1,AA1=2,点P为DD1的中点.
(1)求证:直线BD1∥平面PAC;
(2)求CP与平面BDD1B1所成的角大小;
(3)求点B1到平面PAC的距离.
19.(14分)设椭圆C:的两个焦点为F1,F2,点P在椭圆C上,且PF1⊥F1F2,|PF1|=3,|PF2|=5.
(1)求椭圆C的方程;
(2)点M在椭圆C上,且△MF1F2的面积为2,求点M的坐标.
20.(15分)已知圆C:x2+y2﹣8y+12=0,直线l:ax+y+2a=0.
(1)当直线l与圆C相交,求a的取值范围;
(2)当直线l与圆C相交于A,B两点,且时,求直线l的方程.
21.(15分)如图,在多面体ABCDEF中,梯形ADEF与平行四边形ABCD所在平面互相垂直,AF∥DE,DE⊥AD,AD⊥BD,AF=AD=BD=DE=1.
(1)求证:DE⊥平面ABCD;
(2)求二面角B﹣EF﹣D的余弦值;
(3)判断线段DE上是否存在点Q,使得直线CQ∥平面BEF?若存在,求出的值,若不存在,说明理由.
2023-2024学年北京市育才学校高二(上)期中数学试卷
参考答案与试题解析
一、选择题(共10小题,每小题4分,共40分.在每小题列出的四个选项中,选出符合题目要求的一项.)
1.(4分)直线y=﹣x+2的倾斜角为( )
A.45°B.60°C.120°D.135°
【分析】根据直线的斜率与倾斜角的关系进行求解即可.
【解答】解:由y=﹣x+2可知该直线的斜率为﹣1,
所以该直线的倾斜角135°.
故选:D.
【点评】本题考查了直线的倾斜角问题,考查直线的斜率,是基础题.
2.(4分)已知向量,,则=( )
A.B.14C.D.
【分析】根据空间向量的加法运算求得的坐标,根据模的计算公式,即得答案.
【解答】解:由题意知向量,,
则,
故.
故选:D.
【点评】本题考查了向量坐标的加法运算,根据向量的坐标求向量的长度的方法,是基础题.
3.(4分)两个不同的平面α和β,平面α的一个法向量为,平面β的一个法向量,则平面α与平面β( )
A.平行B.垂直C.相交D.不能确定
【分析】根据的坐标,判断二者共线,即可判断平面α与平面β的位置关系.
【解答】解:由题意知,,
则,即共线,则α∥β,
故选:A.
【点评】本题考查的知识要点:法向量,平面间的位置关系,主要考查学生的理解能力和计算能力,属于中档题.
4.(4分)已知圆M:x2+y2=1与圆N:(x﹣2)2+y2=9,则两圆的位置关系是( )
A.相交B.相离C.内切D.外切
【分析】根据两圆的圆心距与半径的关系,判断两圆的位置关系
【解答】解:圆M:x2+y2=1的圆心为M(0,0),半径为r1=1;
圆N:(x﹣2)2+y2=9的圆心为N(2,0),半径为r2=3;
|MN|=2=r2﹣r1,
∴两圆的位置关系是内切.
故选:C.
【点评】本题考查了两圆位置关系的判断问题,是基础题
5.(4分)若图中的直线l1、l2、l3的斜率分别为k1、k2、k3,则( )
A.k1<k2<k3B.k2<k1<k3C.k2<k3<k1D.k1<k3<k2
【分析】由k=tanα,并结合正切函数的单调性,即可得解.
【解答】解:由k=tanα知,当α∈[0,90°)时,k>0,且k随α的增大而增大,
当α∈(90°,180°)时,k<0,且k随α的增大而增大,
所以k1<k2<k3.
故选:A.
【点评】本题考查直线的斜率与倾斜角的关系,正切函数的单调性,考查逻辑推理能力和运算能力,属于基础题.
6.(4分)已知椭圆上一点P到椭圆一个焦点的距离为4,则它到另一个焦点的距离( )
A.6B.5C.4D.2
【分析】由椭圆标准方程求得长轴长,再由椭圆定义得答案.
【解答】解:由椭圆,得a2=25,a=5.
设P到椭圆另一个焦点的距离为d,
则由椭圆定义可得:4+d=2a=10,即d=6.
∴P到另一个焦点的距离为6.
故选:A.
【点评】本题考查椭圆标准方程,考查椭圆定义的应用,是基础题.
7.(4分)“a=1”是“直线l1:ax+y+2=0与直线l2:x+ay+2=0平行”的( )
A.充要条件
B.充分不必要条件
C.必要不充分条件
D.既不充分也不必要条件
【分析】先根据两直线平行求出a,再根据充分条件和必要条件的定义即可得解.
【解答】解:因为直线l1:ax+y+2=0与直线l2:x+ay+2=0平行,
所以a2﹣1=0,解得a=±1,
经检验当a=1时,两直线重合,
所以a=﹣1,
所以“a=1”是“直线l1与直线l2平行”的既不充分也不必要条件.
故选:D.
【点评】本题主要考查了两直线平行时的斜率关系,是基础题.
8.(4分)已知半径为1的圆经过点(3,4),则其圆心到原点的距离的最小值为( )
A.4B.5C.6D.7
【分析】结合题意画出满足条件的图象,结合图象求出答案即可.
【解答】解:如图示:
半径为1的圆经过点(3,4),可得该圆的圆心轨迹为(3,4)为圆心,1为半径的圆,
故当圆心到原点的距离的最小时,
连结OB,A在OB上且AB=1,此时距离最小,
由OB=5,得OA=4,
即圆心到原点的距离的最小值是4,
故选:A.
【点评】本题考查了圆的基础知识,考查数形结合思想,是一道常规题.
9.(4分)过点A(1,2)且与原点距离最大的直线方程为( )
A.2x+y﹣4=0B.x+2y﹣5=0C.x+3y﹣7=0D.3x+y﹣5=0
【分析】过点A(1,2)且与原点距离最大的直线与OA垂直,再用点斜式方程求解.
【解答】解:根据题意得,当所求直线与直线OA垂直时距离最大,
因直线OA的斜率为2,所以所求直线斜率为﹣,
所以由点斜式方程得:y﹣2=﹣(x﹣1),
化简得:x+2y﹣5=0,
故选:B.
【点评】本题考查直线方程的求解,要数形结合先判断什么时候距离最大才能求直线方程,属基础题.
10.(4分)已知MN是正方体内切球的一条直径,点P在正方体表面上运动,正方体的棱长是2,则的取值范围为( )
A.[0,4]B.[0,2]C.[1,4]D.[1,2]
【分析】建立空间直角坐标系,利用空间向量的数量积求解即可.
【解答】解:以D1为坐标原点,以D1A1,D1C1,D1D所在直线为x轴,y轴,z轴,
建立空间直角坐标系,如图所示;
设正方体内切球球心为S,MN是该内切球的任意一条直径,
则内切球的半径为1,
所以•=(+)•(+)=(+)•(﹣)=﹣1∈[0,2].
所以的取值范围是[0,2].
故选:B.
【点评】本题以正方体为载体,考查了线面、面面位置关系,以及空间向量的数量积应用问题,是中档题.
二、填空题(共5小题,每小题5分,共25分.)
11.(5分)圆x2+y2+2y=1的圆心坐标为 (0,﹣1) ,半径为 .
【分析】将圆的一般方程化为标准方程,即可得答案.
【解答】解:由题意知圆x2+y2+2y=1即圆x2+(y+1)2=2,
故该圆的圆心为(0,﹣1),半径为.
故答案为:(0,﹣1);.
【点评】本题考查的知识要点:圆的方程的转换,主要考查学生的理解能力和计算能力,属于中档题.
12.(5分)一个椭圆的长轴长是短轴长的2倍,则该椭圆的离心率为 .
【分析】由题意,a=2b,再用平方关系算得c=b,最后利用椭圆离心率公式可求出椭圆的离心率.
【解答】解:设椭圆的方程为,(a>b>0)
∵椭圆的长轴长是短轴长的2倍,
∴2a=2×2b,得a=2b
又∵a2=b2+c2
∴4b2=b2+c2,可得c=b
因此椭圆的离心率为e===
故答案为:
【点评】本题给出椭圆长轴与短轴的倍数关系,求椭圆的离心率,考查了椭圆的基本概念和简单性质的知识,属于基础题.
13.(5分)已知点P(x,y)在直线x+y﹣4=0上,O是原点,则OP的最小值是 .
【分析】OP的最小值,就是两点间的距离的最小值,转化为原点的直线的距离.
【解答】解:因为点P(x,y)在直线x+y﹣4=0上,O是原点,则OP的最小值,就是求原点O到直线x+y﹣4=0的距离,
即|OP|=.
故答案为:.
【点评】两点间的距离公式转化为点到直线的距离公式,是一种转化的数学思想.学生要掌握.
14.(5分)试给出一组试两条直线l1:2x﹣y=0与l2:ax+by﹣3=0互相垂直的实数a,b的值 a=1,b=2(满足b=2a且不为零的实数a,b的值均符合) .
【分析】由直线相互垂直可得a,b满足的等式关系,求符合条件的一组a,b的值即可.
【解答】解:两条直线l1:2x﹣y=0与l2:ax+by﹣3=0互相垂直,
则有2a+(﹣1)×b=0,即b=2a.
故答案为:a=1,b=2(满足b=2a且不为零的实数a,b的值均符合).
【点评】本题考查直线的垂直关系,属于基础题.
15.(5分)已知M为椭圆上一点,N为椭圆长轴上一点,O为坐标原点.给出下列结论:
①存在点M,N,使得△OMN为等边三角形;
②不存在点M,N,使得△OMN为等边三角形;
③存在点M,N,使得∠OMN=90°;
④不存在点M,N,使得∠OMN=90°.
其中,所有正确结论的序号是 ①④ .
【分析】利用椭圆的简单几何性质,直接可判断①正确②错误,分情况讨论点M,N的位置,利用余弦定理判断cs∠OMN的取值范围,即可确定③错误,④正确.
【解答】解:∵过原点倾斜角为60°的直线一定与椭圆由交点,
∴假设y轴右侧的交点是M,
在长轴上取ON=OM,
则△OMN就是等边三角形.
故①正确,②错误;
若点M和点N在y轴两侧,
则∠OMN一定是锐角;
若点M和点N在y轴同侧,
不妨设为在y轴的右侧.
设点M(x,y),
则,且0<x<2.
由椭圆性质可知,
当点N是长轴短点时,∠OMN最大,
∵|OM|2=x2+y2,
|MN|2=(x﹣a)2+y2=(x﹣2)2+y2,
|ON|2=a2=4
∴|OM|2+|MN|2
=x2+y2+(x﹣2)2+y2
=2x2﹣4x+4+2y2
=,
在x∈(0,2)上上式恒大于4,
即|OM|2+|MN|2<|ON|2,
∴∠OMN<90°.
故③错误,④正确.
故答案为:①④.
【点评】本题考查椭圆的几何性质的应用,直线与椭圆的位置关系,二次函数在固定区间上的最值等知识的综合应用.属于难题.
三、解答题(共6小题,共85分.解答应写出文字说明,演算步骤或证明过程.)
16.(12分)已知△ABC的顶点坐标为A(﹣1,5)、B(﹣2,﹣1)、C(4,3).
(1)求BC边的中线长;
(2)求AB边的高线所在直线方程.
【分析】(1)根据中线的定义,结合中点坐标公式和两点间距离公式进行求解即可;
(2)根据互相垂直直线的斜率关系,结合直线点斜式方程进行求解即可.
【解答】解:(1)设BC边的中点为D,因为B(﹣2,﹣1)、C(4,3),
所以点D的坐标为,即D(1,1),
所以BC边的中线长.
(2)因为,所以AB边的高线所在直线的斜率为,
因此AB边的高线所在直线方程为.
【点评】本题考查直线的垂直关系,考查直线的一般方程,属于中档题.
17.(14分)求下列各圆的标准方程:
(1)圆心在直线y=﹣x上且过M(2,0)、N(0,﹣4)两点的圆的方程;
(2)经过A(﹣1,﹣1)、B(﹣8,0)、C(0,6)三点的圆的方程.
【分析】(1)直接利用圆的一般式求出圆的方程;
(2)直接利用圆的一般式求出圆的方程.
【解答】解:(1)由于M(2,0)、N(0,﹣4)
设圆的方程为x2+y2+Dx+Ey+F=0,
所以,解得,
故圆的方程为x2+y2﹣6x+6y+8=0;
(2)设圆的方程为x2+y2+Dx+Ey+F=0,由于圆经过A(﹣1,﹣1)、B(﹣8,0)、C(0,6),
故,解得,故圆的方程为x2+y2+8x﹣6y=0.
【点评】本题考查的知识要点:圆的方程的求法.主要考查学生的理解能力和计算能力,属于中档题.
18.(15分)如图,长方体ABCD﹣A1B1C1D1中,AB=AD=1,AA1=2,点P为DD1的中点.
(1)求证:直线BD1∥平面PAC;
(2)求CP与平面BDD1B1所成的角大小;
(3)求点B1到平面PAC的距离.
【分析】(1)利用三角形中位线定理,给合线面平行的判定定理进行证明即可;
(2)根据线面垂直的判定定理,结合线面角定义进行求解即可;
(3)建立空间直角坐标系,利用空间点到面距离公式进行求解即可.
【解答】解:(1)证明:设AC∩BD=O,显然O是BD中点,连接OP,
因为点P为DD1的中点,
所以BD1∥OP,而BD1⊄平面PAC,OP⊂平面PAC,
所以直线BD1∥平面PAC;
(2)因为AB=AD=1,
所以矩形ABCD是正方形,因此AC⊥BD,
又因为DD1⊥平面ABCD,AC⊂平面ABCD,
所以DD1⊥AC,而DD1∩DB=D,DD1,DB⊂平面BDD1B1,
所以AC⊥平面BDD1B1,
所以∠CPO是CP与平面BDD1B1所成的角.
因为AB=AD=1,AA1=2,点P为DD1的中点.
所以,,
在直角三角形CPO中,sin∠CPO==,即有∠CPO=,
所以CP与平面BDD1B1所成的角大小为;
(3)建立如图所示的空间直角坐标系,
P(0,0,1),A(1,0,0),C(0,1,0),B1(1,1,2),
设平面PAC的法向量为,
,
则有,
,
点B1到平面PAC的距离.
【点评】本题考查线面平行的判定、点到平面的距离和线面角的求法,考查转化思想、运算能力、推理能力,属于中档题.
19.(14分)设椭圆C:的两个焦点为F1,F2,点P在椭圆C上,且PF1⊥F1F2,|PF1|=3,|PF2|=5.
(1)求椭圆C的方程;
(2)点M在椭圆C上,且△MF1F2的面积为2,求点M的坐标.
【分析】(1)由题意,根据椭圆定义以及勾股定理进行求解即可;
(2)根据三角形面积公式进行求解即可.
【解答】解:(1)因为点P在椭圆C上,
所以|PF1|+|PF2|=3+5=2a,
解得a=4,
因为PF1⊥F1F2,|PF1|=3,|PF2|=5,
所以,
此时,
解得|F1F2|=4,
所以2c=4,
解得c=2,
又b2=a2﹣c2=12,
则椭圆C的方程为;
(2)不妨设M(x0,y0),
因为△MF1F2 的面积为,
所以,
即,
解得,
因为点M在椭圆C上,
所以,
此时,
解得,
所以点M的坐标为或或或.
【点评】本题考查椭圆的方程,考查了逻辑推理和运算能力.
20.(15分)已知圆C:x2+y2﹣8y+12=0,直线l:ax+y+2a=0.
(1)当直线l与圆C相交,求a的取值范围;
(2)当直线l与圆C相交于A,B两点,且时,求直线l的方程.
【分析】(1)根据圆心到直线的距离小于半径可得a的范围;
(2)根据圆中相交弦长的一半与半径和圆心到直线的距离构成直角三角形,解出参数的值.
【解答】解:(1)圆C:x2+y2﹣8y+12=0化成标准方程为x2+(y﹣4)2=4,则此圆的圆心为(0,4),半径为2,
当直线l与圆 C相交,则有,解得 ;
(2)过圆心C作CD⊥AB于D,则根据题意和圆的性质,,∴,解得a=﹣7或a=﹣1,
故所求直线方程为7x﹣y+14=0或x﹣y+2=0.
【点评】考查圆的相交弦长的计算,属于基础题.
21.(15分)如图,在多面体ABCDEF中,梯形ADEF与平行四边形ABCD所在平面互相垂直,AF∥DE,DE⊥AD,AD⊥BD,AF=AD=BD=DE=1.
(1)求证:DE⊥平面ABCD;
(2)求二面角B﹣EF﹣D的余弦值;
(3)判断线段DE上是否存在点Q,使得直线CQ∥平面BEF?若存在,求出的值,若不存在,说明理由.
【分析】(1)根据面面垂直的性质定理即可证明;
(2)建立空间直角坐标系,求出平面BEF与平面DEF的法向量,利用向量计算二面角的余弦值;
(3)将线面平行转化为直线方向向量与平面法向量垂直进行计算可得.
【解答】解:(1)证明:由题意知:
平面ADEF⊥平面ABCD,平面ADEF∩平面ABCD=AD,
DE⊥AD,DE⊂平面ADEF,
故DE⊥平面ABCD;
(2)由于DE⊥平面ABCD,DC⊂平面ABCD,
故DE⊥DC,而DE⊥AD,AD⊥BD,
故以D为坐标原点,以DA,DB,DE所在直线为x轴,y轴,z轴,
建立空间直角坐标系,如图所示,,
则D(0,0,0),B(0,1,0),F(1,0,1),E(0,0,2),
则=(0,﹣1,2),=(1,﹣1,1),
设平面BEF的一个法向量为=(x,y,z),
则,令z=1,则=(1,2,1),
平面DEF的一个法向量可取=(0,1,0),
则cs<>==,
由图可知二面角B﹣EF﹣D为锐角,
故其余弦值为;
(3)假设线段DE上存在点Q,使得直线CQ∥平面BEF,又C(﹣1,1,0),
设Q(0,0,t),0≤t≤2,则CQ=(1,﹣1,t),
则=(1,﹣1,t)•(1,2,1)=0,即1﹣2+t=0,得t=1,
即Q(0,0,1),此时=1,
即线段DE上存在点Q,为DE中点,使得直线CQ∥平面BEF,则.
【点评】本题考查线面垂直的判定,考查二面角的求法,考查线面平行的判定,属中档题.
声明:试题解析著作权属菁优网所有,未经书面同意,不得复制发布日期:2024/7/17 10:05:57;用户:笑涵数学;邮箱:15699920825;学号:36906111
相关试卷
这是一份2023-2024学年北京市东北师大朝阳学校高二(上)期中数学试卷,共4页。
这是一份2022-2023学年北京市十一学校高二(上)期中数学试卷,共18页。
这是一份2022-2023学年北京市清华附中朝阳学校高二(上)期中数学试卷,共22页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。






![[数学]2023-2024学年北京市育才学校高二(上)期中试卷](http://jx-previews-01.oss-cn-hangzhou.aliyuncs.com/3/3/16207811/0-1727698066269/0.jpg?x-oss-process=image/resize,w_202)


