江苏省盐城市大丰区实验初中教育集团联考2024-2025学年九年级上学期10月期中考试数学试题

这是一份江苏省盐城市大丰区实验初中教育集团联考2024-2025学年九年级上学期10月期中考试数学试题，共13页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

1.在下列方程中，属于一元二次方程的是（ ）
A．10x2＝9B．2（x﹣1）＝3xC．D．x2﹣y2＝6
2.下列关于圆的说法中，正确的是（ ）
A. 三点确定一个圆 B. 一个圆只有一个内接三角形
C. 圆心相同的圆是同心圆 D. 等弧所对的圆心角相等
3.用配方法解方程，配方正确的是( )
A. B. (C. D.
4.小敏参加了某次演讲比赛，根据比赛时七位评委所给的分数制作了如下表格：
如果去掉一个最高分和一个最低分，那么表格中数据一定不发生变化的是（）
A. 平均数B. 中位数C. 众数D. 方差
5.如图，小球从口往下落，在每个交叉口都有向左或向右两种可能，且可能性相同，则小球最终从口落出的概率为（ ）
A.B.C.D.

第5题图 第6题图 第7题图 第8题图
6．如图，在边长为2的正八边形中，把其不相邻的四条边均向两边延长相交成一个四边形ABCD，则四边形ABCD的周长是（ ）
A．24B．12C．16D．8+8
7. 如图，在平面直角坐标系中，已知点A（0，1）、点B（0，1+t）、C（0，1﹣t）（t＞0），点P在以D（3，5）为圆心，1为半径的圆上运动，且始终满足∠BPC=90°，则t的最小值是（ ）
A. 3B. 4C. 5D. 6
8．如图所示，边长为4的正方形内接于⊙O，点E是上的一个动点（不与A、B重合），点F是上的一点，连接，分别与交于点G、H，且，有下列结论：①；②是等腰直角三角形；③四边形的面积不随点E位置的变化而变化；③周长的最小值为．其中正确的是（ ）
A．①②③B．②③④C．①②④D．①②③④
二、填空题（每题3分，计30分）
9．若，则代数式的值为 ．
10.设x1，x2是方程2x2+4x﹣3=0的两个实数根，则（x1﹣2）（x2﹣2）= ．
11．直角三角形的两条边长分别为3和4，那么这个三角形的外接圆半径等于 ．
12．如图，将含60°角的直角三角极ABC绕顶点A顺时针旋转45°度后得到△AB′C′，点B经过的路径为弧BB′．若∠BAC=60°，AC=1，则图中阴影部分的面积是 ．
13．任意抛掷一枚均匀的骰子，骰子各个面的点数分别为1，2，3，4，5，6，则朝上的点数是奇数的概率是 ．
14．为迎接全市的禁毒知识竞赛，某校进行了相关知识测试，经过层层预赛，小洋和小亮进入了最后的决赛，如图，是他们6次的测试成绩，若要从中选一名测试成绩稳定的同学去参加竞赛，则应选 .（填“小洋”或“小亮”）．


第12题 第14题
15．如图，是⊙O的内接三角形，，直径CD垂直于弦AB于点E，连接AD．若，则AD的长为 ．
16．如图，在中，，的内切圆与分别相切于点D、E、F，若的半径为2，，则的长 ．
17．如图有一个三角形点阵，从上向下有无数多行，其中第一行有个点，第二行有个点，，第行有个点，容易发现，10是三角点阵中前行的点数之和当三角点阵中点数之和是时，则三角点阵点的行数为 ．
18．如图，在矩形中，，，点分别是边上的动点，且，点是的中点，连接，则四边形面积的最小值为 ．

第15题 第16题 第17题 第18题
三、解答题（共9题，计96分）
19．解方程：
（1）x2﹣14x+21＝0．
（2）3x2﹣6x＝4（x﹣2）．
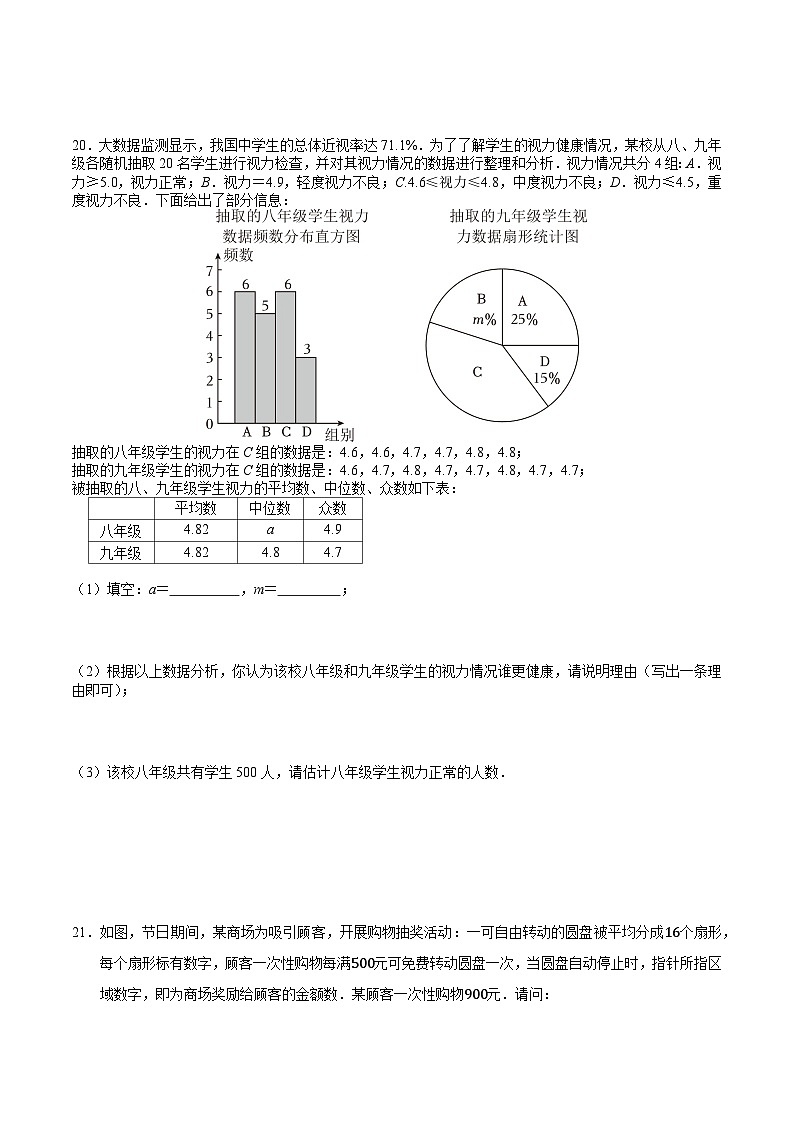
20．大数据监测显示，我国中学生的总体近视率达71.1%．为了了解学生的视力健康情况，某校从八、九年级各随机抽取20名学生进行视力检查，并对其视力情况的数据进行整理和分析．视力情况共分4组：A．视力≥5.0，视力正常；B．视力＝4.9，轻度视力不良；C.4.6≤视力≤4.8，中度视力不良；D．视力≤4.5，重度视力不良．下面给出了部分信息：
抽取的八年级学生的视力在C组的数据是：4.6，4.6，4.7，4.7，4.8，4.8；
抽取的九年级学生的视力在C组的数据是：4.6，4.7，4.8，4.7，4.7，4.8，4.7，4.7；
被抽取的八、九年级学生视力的平均数、中位数、众数如下表：
（1）填空：a＝ ，m＝ ；
（2）根据以上数据分析，你认为该校八年级和九年级学生的视力情况谁更健康，请说明理由（写出一条理由即可）；
（3）该校八年级共有学生500人，请估计八年级学生视力正常的人数．
21．如图，节日期间，某商场为吸引顾客，开展购物抽奖活动：一可自由转动的圆盘被平均分成16个扇形，每个扇形标有数字，顾客一次性购物每满500元可免费转动圆盘一次，当圆盘自动停止时，指针所指区域数字，即为商场奖励给顾客的金额数．某顾客一次性购物900元．请问：
(1)他转动一次转盘获得100元奖励的概率是多少？
(2)如果是你，是参加一次抽奖还是再购买100元的商品参加两次次抽奖？做出你的选择并简单说明你的理由．
22．如图，是直角三角形的外接圆，直径，过C点作的切线，与延长线交于点D，M为的中点，连接，，且与相交于点N．
(1)求证：与相切；
(2)当时，在的圆上取点F，使，补全图形，并求点F到直线的距离．
23．已知关于x的方程2x2+kx-1＝0．
（1）求证：方程有两个不相等的实数根．
（2）若方程的一个根是-1，求方程的另一个根．
24．定义：一元二次方程，若根的判别式是一个完全平方数（式），则此方程叫“完美方程”．
(1)判断下列方程一定是“完美方程”的是 ；（直接填序号）
①；②；③；
(2)若关于的一元二次方程
①证明：此方程一定是“完美方程”；
②设方程的两个实数根分别为，，是否存在实数，使得始终在函数的图像上？若存在，求出的值；若不存在，请说明理由．
25．云南某地一村民，2021年承包种植橙子树200亩，由于第一年收成不错，该村民每年都增加种植面积，到2023年共种植288亩．假设每年的增长率相同．
（1）求该村民这两年种植橙子亩数的平均增长率．
（2）某水果批发店销售该种橙子，市场调查发现，当橙子售价为18元/千克时，每天能售出120千克，售价每降低1元，每天可多售出15千克，为了减少库存，该店决定降价促销，已知该橙子的平均成本价为8元/千克，若使销售该种橙子每天获利840元，则售价应降低多少元？
26.如图所示，四边形是半径为r的的内接四边形，是的直径，，直线l与三条线段、、的延长线分别交于点E、F、G．且满足．
(1)求证：直线直线；
(2)若．
①求证：；
②若半径，求四边形ABCD的周长．
27．阅读理解：
（1）【学习心得】
学习完“圆”这一章内容后，有一些几何问题，如果添加辅助圆，可以使问题变得容易．我们把这个过程称为“化隐圆为显圆”．这类题目主要是两种类型．

①类型一，“定点+定长”：如图1，在中，，，D是外一点，且，求的度数．
解：若以点A（定点）为圆心，（定长）为半径作辅助圆，（请你在图1上画圆）则点C、D必在上，是的圆心角，而是圆周角，从而可容易得到 °．
②类型二，“定角+定弦”：如图，中，，，P是内部的一个动点，且满足，求线段长的最小值．
解：∵，
∴，∵，∴，
∴ ，（定角）
∴点P在以（定弦）为直径的上，请完成后面的过程．
（2）【问题解决】
如图3，在矩形中，已知，点P是边上一动点（点P不与B，C重合），连接，作点B关于直线的对称点M，则线段的最小值为 ．
（3）【问题拓展】
如图4，在正方形中，，动点E，F分别在边，上移动，且满足．连接和，交于点P．
①请你写出与的数量关系和位置关系，并说明理由；
②点E从点D开始运动到点C时，点P也随之运动，请求出点P的运动路径长
参考答案
1-4ADBB 5-8CDBA
10.5 11．或2 12． 13.½ 14.小亮 15. 16.10 17.24 18.142
19.解：（1）∵x2﹣14x+21＝0，
∴x2﹣14x＝﹣21，
∴x2﹣14x+49＝﹣21+49，
即（x﹣7）2＝28，
∴，
∴，；
（2）移项提取公因式得，3x（x﹣2）﹣4（x﹣2）＝0，
因式分解得，（x﹣2）（3x﹣4）＝0，
∴x﹣2＝0或3x﹣4＝0，
∴x1＝2，．
20.解：(1)八年级学生的视力按从小到大的顺序排序后，第10个数据和第11个数据都是4.9, :a=4.9+4.9=49, 20×25%=5,20×%15=3,C组人数为8,
∴.B组人数为20-5-3-8=4,∴m%=240×100%=20%,∴m=20,故答案为：4.9,20;
(2)∵八年级和九年级学生的视力的平均数相等，而八年级学生的视力的中位数和众数均高于九年级，∴八年级学生的视力情况谁更健康；
(3)500×0=150(人),估计八年级学生视力正常的人数为150人。
21.(1)18
(2)如果是我，我会选再购买100元的商品参加两次次抽奖
22.（1）证明：连接，
为的中点，是中点，
，
是的直径，
，
，
∵，
，
又
，
，
是切线
，
，
，
是切线；
（2）如图所示，当点在上时，连接，交于点，
，
，
，
，
直径，
，
∴，
，
；
当点在半圆上时，过点作，垂足为点，，垂足为点，
四边形是矩形，
在中，，
∵，
∴，
，
∴，
，
．
23.（1）证明：Δ＝b2﹣4ac＝k2﹣4×2×（﹣1）＝k2+8．
∵k2≥0，
∴k2+8＞0，即Δ＞0，
∴方程有两个不相等的实数根．
（2）解：设方程的另一个根为x1，
依题意得：﹣1•x1＝﹣12，
解得：x1＝12，
∴方程的另一个根为12．
24.（1）解：①，
，不是完全平方数，
不是“完美方程”；
②，
，不是完全平方式，
不是“完美方程”；
③，
，是完全平方式，
是“完美方程”；
故答案为：③；
（2）解：①证明：
，且是完全平方数，
此方程一定是“完美方程”；
②存在，理由如下：
，
，
或，
或，
设方程的两个实数根分别为、，
，，
始终在函数的图像上，
，
，
即存在实数，使得Px1,x2始终在函数的图像上，的值为
25.解：（1）设该村民这两年种植橙子亩数的平均增长率为x，
根据题意得：200（1+x）2＝288，
解得：x1＝0.2＝20%，x2＝﹣2.2（不符合题意，舍去）．
答：该村民这两年种植橙子亩数的平均增长率为20%；
（2）设售价应降价y元，则每千克的销售利润为（18﹣y﹣8）元，每天能售出（120+15y）千克，
根据题意得：（18﹣y﹣8）（120+15y）＝840，
整理得：y2﹣2y﹣24＝0，
解得：y1＝6，y2＝﹣4（不符合题意，舍去）．
答：售价应降低6元．
26.（1）证明：在中，
，
，即，
在中，
，
，
即直线直线；
（2）解：①四边形是半径为r的的内接四边形，
，
，
，
是的直径，
，
由（1）可知，
，
在与中，
，
，
②在中，，
，
是的直径，
，
，
，
，
在中，
，
即，
解得：，
由①可知，
，
，
四边形的周长为：
．
27.（1）①∵，，
∴点B，点C，点D在以点A为圆心，为半径的圆上，

如图1，．
（2），，
，，，
点在以（定弦）为直径的上，
如图2，连接交于点，此时最小，

点是的中点，，
在中，，，，
，．
最小值为4．
（2）如图3，连接，

点，点关于直线对称，
，点在以点为圆心，为半径的圆上运动，
当点在线段上时，有最小值，
，，，
∴的最小值为．
（3）①结论：，
理由：∵四边形是正方形，
∴，
∵，
在和中，
∴，
∴，，
，，，
，．
②如图4，连接，交于点O，
∵点P在运动中保持，
平均数/分
中位数/分
众数/分
方差/
平均数
中位数
众数
八年级
4.82
a
4.9
九年级
4.82
4.8
4.7