

四川省2023_2024学年高三数学上学期9月月考理试题含解析
展开
这是一份四川省2023_2024学年高三数学上学期9月月考理试题含解析,共22页。试卷主要包含了 已知,则, 已知命题,命题,则, 函数的图象大致形状为., 已知命题p等内容,欢迎下载使用。
第I卷(选择题)
一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1. 已知,则()
A. B.
C. D.
【答案】D
【解析】
【分析】根据题意理解集合A,B,进而结合交集的概念分析判断.
【详解】因为集合A是2的倍数组成的集合,集合B是3的倍数组成的集合,
可得集合A与集合B的公共元素为6的倍数,
所以.
故选:D.
2. 已知命题,命题,则()
A. “”是假命题B. “”是真命题
C. “”假命题D. “”是真命题
【答案】D
【解析】
【分析】先判断命题、命题的真假,再根据复合命题的真假判定,结合选项即可求解.
【详解】命题,如:当时,
不等式成立,所以为真命题,为假命题;
命题,当时,不等式不成立,
所以为假命题,为真命题,
故“”是真命题,“”是假命题,
“”是真命题,“”是真命题,
故选:D.
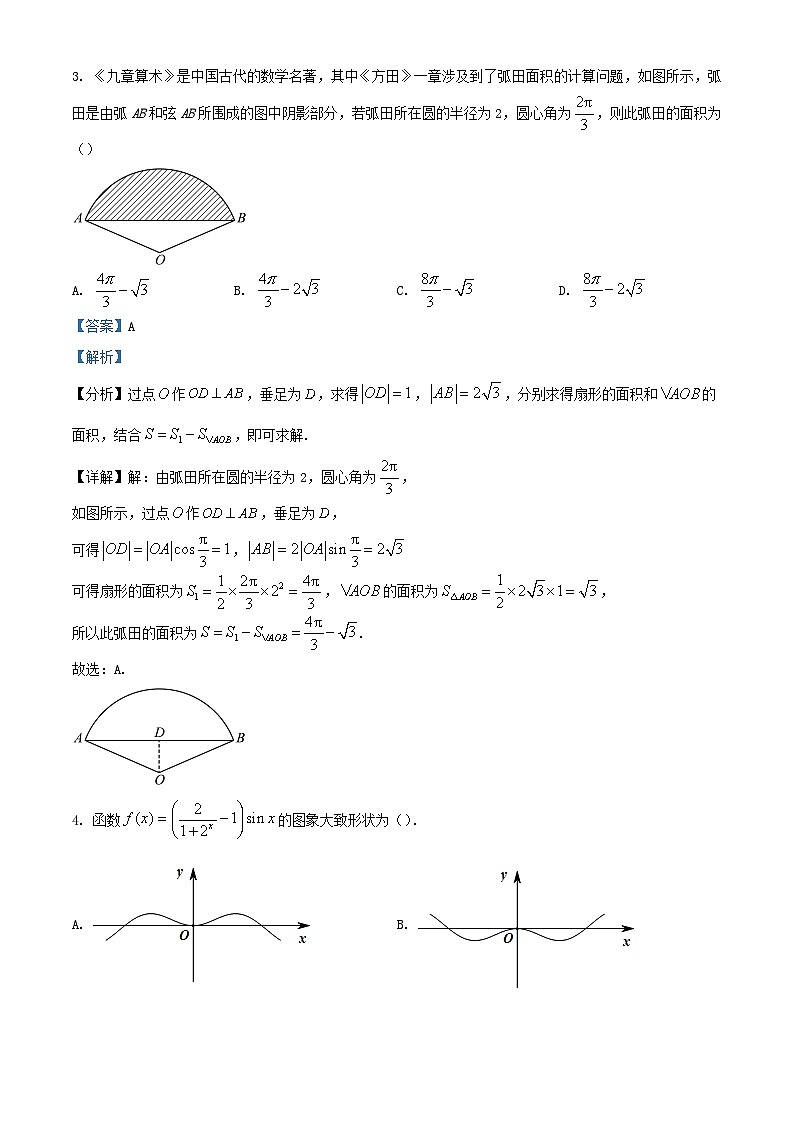
3. 《九章算术》是中国古代的数学名著,其中《方田》一章涉及到了弧田面积的计算问题,如图所示,弧田是由弧AB和弦AB所围成的图中阴影部分,若弧田所在圆的半径为2,圆心角为,则此弧田的面积为()
A. B. C. D.
【答案】A
【解析】
【分析】过点作,垂足为,求得,,分别求得扇形的面积和的面积,结合,即可求解.
【详解】解:由弧田所在圆的半径为2,圆心角为,
如图所示,过点作,垂足为,
可得,
可得扇形的面积为,的面积为,
所以此弧田的面积为.
故选:A.
4. 函数的图象大致形状为().
A. B.
C. D.
【答案】B
【解析】
【分析】
首先判断函数的奇偶性,再判断时,函数值的正负,判断得选项.
【详解】因为,所以,
,
所以函数是偶函数,关于轴对称,排除C,D,
令,则或,解得,而时,,,,此时.故排除A.
故选:B.
【点睛】思路点睛:函数图象的辨识可从以下方面入手:
(1)从函数的定义域,判断图象的左右位置;从函数的值域,判断图象的上下位置.
(2)从函数的单调性,判断图象的变化趋势;
(3)从函数的奇偶性,判断图象的对称性;
(4)从函数的特征点,排除不合要求的图象.
5. 已知,则()
A. B.
C. D.
【答案】D
【解析】
【分析】根据反例可判断AC,根据不等式的性质,结合函数的单调性即可判断BD.
详解】对于A,若,显然满足,但不能得到,故A错误,
对于B,由于,所以,又为单调递增函数,所以,故B错误,
对于C,若,显然满足,,故C错误,
对于D,若,则,函数在上单调递增,所以,
当,则,函数在上单调递增,所以,
当,则,综上可知D正确,
故选:D
6. 如图的程序框图的算法思路源于欧几里得在公元前300年左右提出的“辗转相除法”.执行该程序框图,若输入,则输出的值为()
A. 4B. 37C. 148D. 333
【答案】B
【解析】
【分析】利用辗转相除法求1813和333的最大公约数.
【详解】题中程序框图为辗转相除法求1813和333的最大公约数.
因为,,,
所以1813和333的最大公约数为37.
故选:B.
7. 已知函数,若,则()
A. B. C. D. 1
【答案】A
【解析】
【分析】根据分段函数每段都是单调的可知,且,代入解析式求解即可.
【详解】由可知函数每段上都为减函数,
所以由可知,且
所以,
解得.
故选:A
8. 已知命题p:函数在上单调递减;命题,都有.若为真命题,为假,则实数a的取值范围为().
A. B.
C. D.
【答案】A
【解析】
【分析】根据题意求出为真命题时的范围,进而根据 中一真一假分两类情况讨论即可求解.
【详解】若命题p为真,则,若为真,则 ,
由于为真命题,为假,则 中一真一假
若 真 假,则满足: ;
若 真 假,则满足: ,此时 无解,
综上
故选:A
9. 函数在区间上单调递减的必要不充分条件是()
A. B.
C. D.
【答案】C
【解析】
【分析】由复合函数的单调性与充分必要条件的概念判断,
【详解】设.
∵在上单调递减,
∴由复合函数的单调性法则可知,在上单调递减,且在上恒成立.
(注意对数的真数在上大于0)
又在上单调递减,(若函数在上单调递减,则)
∴解得.
则可得函数在区间上单调递减的充要条件是.
而所求的是函数在区间上单调递减的必要不充分条件,
故只需看是哪一个的真子集,
故选:C
10. 已知二次函数,且不等式的解集为.若不等式在上有解,则实数的取值范围为()
A. B. C. D.
【答案】B
【解析】
【分析】根据不等式解集端点为对应方程的根求出,由原不等式分离参数后换元,再由均值不等式求最值即可得解.
【详解】的解集为,
方程的两根为1和3,
,解得,
所以由可得,
,
,
设,则有解,
,当且仅当,即时取得最大值.
,即实数的取值范围为.
故选:B
11. 若函数满足,且时,,已知函数则函数在区间内的零点个数为()
A. 14B. 13C. 12D. 11
【答案】C
【解析】
【分析】由题设易知是周期为2函数,结合函数解析式画出、的函数图象,判断它们在的交点个数即可.
【详解】因为,则,
所以是周期为2函数,
因为时,则、的图象如下:
时且递增,时且递减,时且递增,
又,,,
由图知:区间上函数交点共有12个.
故选:C.
12. 已知,,,则()
A. B.
C. D.
【答案】C
【解析】
【分析】构造函数,利用导数研究其单调性,从而得到;再构造函数,进而得到,由此得解.
【详解】令,,
则,故在上单调递减,
所以,即,即,故;
令,则,所以在上单调递减,在上单调递增,所以,
令,
所以,所以在上单调递增,
,
所以,所以;
综上:.
故选:C.
【点睛】方法点睛:导函数中常用的两种常用的转化方法:
一是利用导数研究含参函数的单调性,常化为不等式恒成立问题.注意分类讨论与数形结合思想的应用;
二是函数的零点、不等式证明常转化为函数的单调性、极(最)值问题处理.
第II卷(非选择题)
二、填空题:本大题共4小题,每小题5分,共20分.把答案填在答题卡上.
13. 设函数________.
【答案】
【解析】
【分析】利用分段函数的解析式求出和再相加可得结果.
【详解】,
,
,
.
故答案为:.
14. 若,则_________.
【答案】0
【解析】
【详解】设.
则
.
15. 定义在上的函数满足是偶函数,且,若,则______
【答案】##
【解析】
【分析】由已知结合函数的奇偶性及对称性可求出函数的周期,然后结合周期,利用赋值法即可求得结果.
【详解】因为是偶函数,所以,
因为,
所以,
所以,所以,
所以的周期为6,
因为,,所以,
所以,所以,
所以,
故答案为:
16. 已知函数,若函数有四个不同的零点、、、,且,则以下结论正确的是_____.
①;
②;
③;
④.
【答案】①②④
【解析】
【分析】设,其中,利用导数分析函数的单调性与极值,数形结合可判断②的正误;分析可知,结合基本不等式可判断①的正误;构造函数,利用导数分析函数在上的单调性,可判断③④的正误.
【详解】设,其中,则,
当时,,此时函数单调递增,
当时,,此时函数单调递减,
所以,函数的极大值为,且当时,,
作出函数、的图象如下图所示:
由图可知,当时,直线与函数的图象有四个交点,②对;
因为,则,由图可知,则,
所以,,①对;
令,其中,由图可知,
,
当时,,则,此时函数单调递减,
所以,,即,
因为,,且函数在上单调递减,
所以,,则,故,③错④对.
故答案为:①②④.
【点睛】方法点睛:证明极值点偏移的相关问题,一般有以下几种方法:
(1)证明(或):
①首先构造函数,求导,确定函数和函数的单调性;
②确定两个零点,且,由函数值与的大小关系,得与零进行大小比较;
③再由函数在区间上单调性得到与的大小,从而证明相应问题;
(2)证明(或)(、都为正数):
①首先构造函数,求导,确定函数和函数的单调性;
②确定两个零点,且,由函数值与的大小关系,得与零进行大小比较;
③再由函数在区间上的单调性得到与的大小,从而证明相应问题;
(3)应用对数平均不等式证明极值点偏移:
①由题中等式中产生对数;
②将所得含对数的等式进行变形得到;
③利用对数平均不等式来证明相应的问题.
三、解答题:本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.
(一)必考题:(本大题共5小题,每小题12分,共60分)
17. 在平面直角坐标系中,角以Ox为始边,它的终边与单位圆交于第二象限内的点.
(1)若,求及的值;
(2)若,求点的坐标.
【答案】(1),
(2)
【解析】
【分析】(1)根据三角函数定义以及三角函数诱导公式直接计算求解即可;
(2)根据同角三角函数关系的转化求得进而求解即可.
【小问1详解】
若角以Ox为始边,它的终边与单位圆交于第二象限内的点,
若,则,则,
可得
【小问2详解】
由题意知,
又,①
两边平方,可得,可得,
可得,②
联立①②,可得
所以点P的坐标为
18. 已知函数在处取得极值0.
(1)求;
(2)若过点存在三条直线与曲线相切,求买数的取值范围.
【答案】(1)
(2)
【解析】
分析】(1)根据题意可得,即可得解;
(2)切点坐标为,根据导数的几何意义可得切线方程为,从而可得,再根据过点存在3条直线与曲线相切,等价于关于的方程有三个不同的根,利用导数求出函数的单调区间及极值,即可得解.
【小问1详解】
由题意知,
因为函数在处取得极值0,
所以,解得,
经检验,符合题意,所以;
【小问2详解】
由(1)可知,函数,所以,
设切点坐标为,
所以切线方程为,因为切线过点,
所以,即,
令,则,
令,解得,或,
当变化时,的变化情况如下表所示,
因此,当时,有极小值,
当时,有极大值,
过点存在3条直线与曲线相切,
等价于关于的方程有三个不同的根,则,
所以实数的取值范围是.
【点睛】方法点睛:利用导数解决函数零点问题的方法:
(1)直接法:先对函数求导,根据导数的方法求出函数的单调区间与极值,根据函数的基本性质作出图象,然后将问题转化为函数图象与轴的交点问题,突出导数的工具作用,体现了转化与化归思想、数形结合思想和分类讨论思想的应用;
(2)构造新函数法:将问题转化为研究两函数图象的交点问题;
(3)参变量分离法:由分离变量得出,将问题等价转化为直线与函数的图象的交点问题.
19. “硬科技”是以人工智能,航空航天,生物技术,光电芯片,信息技术,新材料,新能源,智能制造等为代表的高精尖技术,属于由科技创新构成的物理世界,是需长期投入,持续积累才能形成的原创技术,具有极高技术门槛和技术壁垒,难以被复制和模仿.最近十年,我国的一大批自主创新的企业都在打造自己的科技品牌,某高科技企业自主研发了一款具有自主知识产权的高级设备,并从2024年起全面发售,假设该高级设备的年产量为x百台,经测算,生产该高级设备每年需投入固完成本1500万元,最多能够生产80百台,每生产一百台台高级设备需要另投成本万元,且,每台高级设备售价为2万元,假设每年生产的高级设备能够全部售出.
(1)求企业获得年利润(万元)关于年产量x(百台)的函数关系式(利润销售收入成本);
(2)当该产品年产量为多少时,企业所获年利润最大?并求最大年利润.
【答案】(1)
(2)当年产量为60百台时,公司获利最大,且最大利润为1250万元
【解析】
【分析】(1)由条件根据利润和销售收入,成本之间的关系求出年利润与年产量之间的关系;
(2)分区间,结合二次函数性质和基本不等式求年利润的最大值.
【小问1详解】
∵,
∴当时,
.
当时,
.
综上所述,.
【小问2详解】
由(1)得
∴当时,
∴当时,(万元)
当时,
(万元)
当且仅当,即时等号成立.
又.
故当年产量为60百台时,公司获利最大,且最大利润为1250万元.
20. 已知函数=(m)是定义在R上的奇函数
(1)求m的值
(2)根据函数单调性的定义证明在R上单调递增(备注:>0)
(3)若对,不等式)0恒成立,求实数k的取值范围.
【答案】(1);
(2)证明见解析;(3).
【解析】
【分析】(1)由奇函数性质求得参数值,再验证符合题意即可;
(2)根据单调性的定义证明;
(3)由奇函数化不等式为,再由增函数化为,然后由一元二次不等式恒成立得结论.
【小问1详解】
是奇函数,∴,,
时,,满足,是奇函数,
所以;
【小问2详解】
设任意两个实数满足,
则,
∵,∴,,∴,即,
所以在R上为单调递增;
【小问3详解】
原不等式化为,
∵是奇函数,∴不等式化为,
又是增函数,所以,
∴问题转化,恒成立,
设,,
,即时,,.
,即时,,无解;
,即时,,无解;
综上,.
【点睛】方法点睛:关于具有奇偶性和单调性函数的不等式恒成立问题,解题方法是利用奇偶性化不等式为,再由单调性化去“”,转化为一般的不等式,如一元二次不等式恒成立问题,再根据不等式的知识求得参数范围.
21. 已知函数.
(1)当时,求函数在区间上的最大值;
(2)若为函数的极值点,求证:
【答案】(1)
(2)证明见解析
【解析】
【分析】(1)求定义域,求导,得到函数的单调性,分,和三种情况,求解函数在上的最大值;
(2)根据极值点定义得到,要证,只需证,令,得到单调性,从而求出,分和两种情况,结合放缩法,构造函数法进行证明.
【小问1详解】
定义域为,则,
当时,,,
所以单调递增区间为,单调递减区间为;
若,即时,在上单调递减,故;
若,即时,在上单调递增,在上单调递减,
故;
若,即时,则在上单调递增,故.
所以,;
【小问2详解】
(),
则,
因为是函数的极值点,所以,即,
要证,
只需证,即证:,
令,则,
当时,,单调递增;当时,,单调递减;
所以,即:,
所以,所以,
①当时,因为,,所以.
②当时,因为,所以,
所以,要证,
只需证,
即证对任意的恒成立,
令(),则,
当时,,单调递增;当时,,单调递减,
所以,
即当时,成立.
综上:原不等式成立.
【点睛】思路点睛:隐零点的处理思路:
第一步:用零点存在性定理判定导函数零点的存在性,其中难点是通过合理赋值,敏锐捕捉零点存在的区间,有时还需结合函数单调性明确零点的个数;
第二步:虚设零点并确定取范围,抓住零点方程实施代换,如指数与对数互换,超越函数与简单函数的替换,利用同构思想等解决,需要注意的是,代换可能不止一次.
(二)选考题(共10分,请在第22、23题中任选一题作答.如果多做,则按所做的第一题记分)
22. 在极坐标系中,是经过点且倾斜角为的直线,曲线的极坐标方程为.
(1)求的极坐标方程;
(2)若曲线的极坐标方程为,设与和的交点分别为,,求.
【答案】(1)
(2)
【解析】
【分析】(1)求的直角坐标方程,再化为极坐标方程;
(2)通过联立方程组,,由可求值.
【小问1详解】
由题意得的直角坐标方程为,即,
化为极坐标方程为,化简得.
【小问2详解】
曲线的极坐标方程为,设与和的交点分别为,,
由,解得,
由,解得,
所以.
23. 已知函数.
(1)若时,恒成立,求的取值范围;
(2)若的最小值为1,求的值.
【答案】(1)
(2)或
【解析】
【分析】(1)分类讨论,可知且当时,恒成立,利用端点值的大小关系列式可求出结果;
(2)分类讨论,去绝对值将化为分段函数,求出其最小值,结合已知最小值列式,可求出结果.
【小问1详解】
当时,因为,所以,,不合题意;
当时,由,得,得,,
因为时,恒成立,所以,解得.
【小问2详解】
,
因为,令,得;令,得,
若,则,则,
则在上为减函数,在上为增函数,在上为增函数,
所以,解得;
若,则,,不符合题意;
当时,,则,
则在上为减函数,在上为增函数,在上为增函数,
所以,解得;
当时,,则,
则在上为减函数,在上为减函数,在上为增函数,
所以,不符合题意;
1
-
0
+
0
-
单调递减
单调递增
0
单调递减
相关试卷
这是一份四川省成都市2023_2024学年高三数学上学期10月月考理试题含解析,共19页。试卷主要包含了 设集合,集合,,则, 已知复数, 展开式中的系数为, 函数的图像大致为, 设,则, 某四面体的三视图如图所示等内容,欢迎下载使用。
这是一份内蒙古包头市2023_2024学年高三数学上学期第一次月考理试题含解析,共14页。试卷主要包含了 设,则a,b,c的大小关系为, 函数y=的图象可能是等内容,欢迎下载使用。
这是一份四川省成都市2023_2024学年高三数学上学期期中试题理含解析,共24页。试卷主要包含了本试卷分选择题和非选择题两部分,考试结束后,只将答题卡交回等内容,欢迎下载使用。









