

专题05 解直角三角形(考点清单,知识导图+3个考点清单+5种题型解读)原卷版-2024-2025学年九年级数学上学期期中考点大串讲(沪教版)
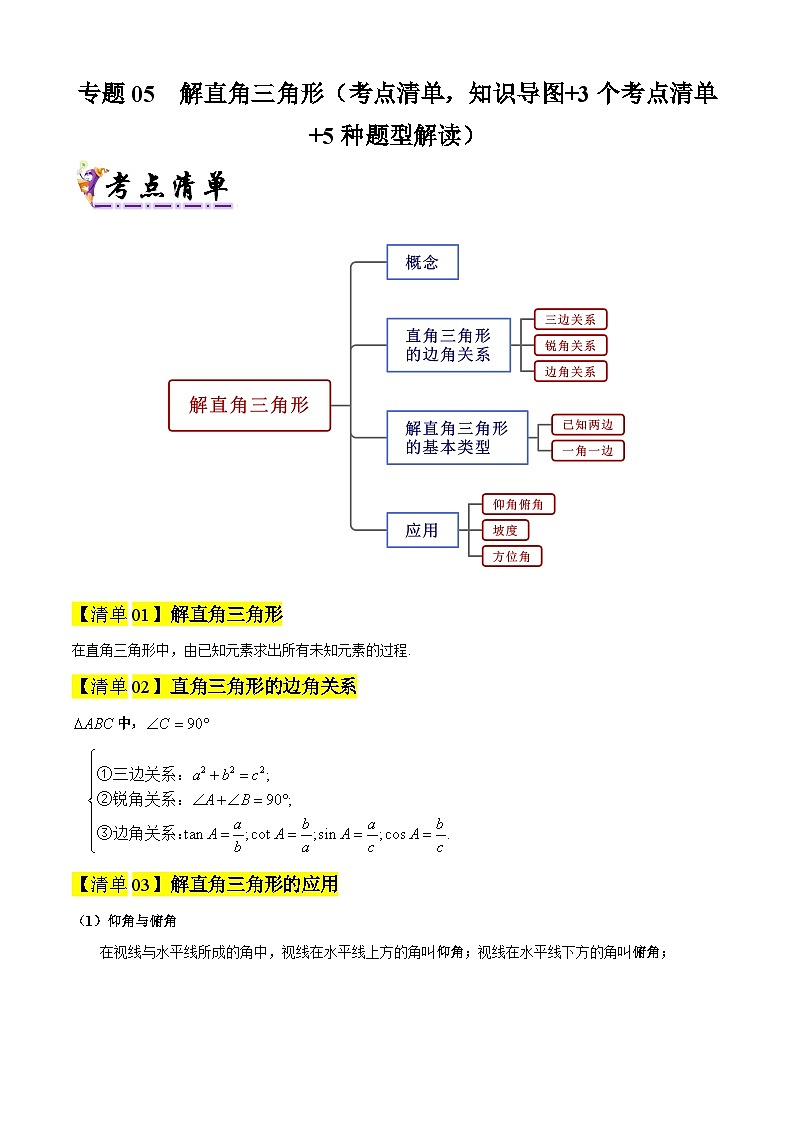
展开【清单01】解直角三角形
在直角三角形中,由已知元素求出所有未知元素的过程.
【清单02】直角三角形的边角关系
中,
【清单03】解直角三角形的应用
(1)仰角与俯角
在视线与水平线所成的角中,视线在水平线上方的角叫仰角;视线在水平线下方的角叫俯角;
(2)坡度:坡面的铅垂高度h和水平宽度的比叫做坡面的坡度,记作,即;坡度表示形式:.
坡面与水平面的夹角叫坡角,记为;坡度与坡角的关系:.
【考点题型一】解直角三角形(共7小题)
【例5】(2023秋•宝山区期中)已知平面直角坐标系中,第一象限内射线与轴正半轴的夹角为,点在射线上,如果,且,那么点的坐标是
A.B.C.D.
【变式1-1】(2023秋•松江区期中)在中,,,,则的长为
A.B.C.D.
【变式1-2】(2022秋•青浦区校级期末)如图,在边长为1个单位的方格纸中,的顶点在小正方形顶点位置,那么的正切值为 .
【变式1-3】(2022秋•虹口区期中)已知中,,,,那么的长是 .
【变式1-4】(2023秋•浦东新区校级期中)如图,在中,,,,,则线段的长 .
【变式1-5】(2023•徐汇区二模)如图,、分别是边上的高和中线,已知,.
(1)求的长;
(2)求的值.
【变式1-6】(2023秋•宝山区期中)如图,中,,,是边的中点,联结.
(1)已知,求的长;
(2)求的值.
【考点题型二】解直角三角形的应用(共6小题)
【例2】(2024•浦东新区三模)图1是第七届国际数学教育大会会徽,在其主体图案中选择两个相邻的直角三角形,恰好能组合得到如图2所示的四边形.若,,则的值为
A.B.C.D.
【变式2-1】(2024•浦东新区三模)某停车场入口“曲臂直杆道闸”在工作时,一曲臂杆绕点匀速旋转,另一曲臂杆始终保持与地面平行.如图1,是曲臂直杆道闸关闭时的示意图,此时、、在一条直线上.已知闸机高度为,,,入口宽度为.
(1)如图2,因机器故障,曲臂杆最多可逆时针旋转,求此时点到地面的距离;
(2)在(1)的条件下,一辆宽为、高为的货车可否顺利通过入口?请说明理由.(参考数据:,
【变式2-2】(2024•上海模拟)如图,某校有一块三角形空地,,为了更好的落实“双减”政策,丰富孩子们的课业生活,学校计划将该三角形空地改造成多功能区域,现要求将三角形区域设计成手工制作区,其余部分设计成健身区,经测量:米,米,米,米.
(1)求的度数;
(2)求图中健身区(阴影部分)的面积.
【变式2-3】(2023秋•虹口区期末)如图①是某款智能磁吸键盘,如图②是平板吸附在该款设备上的照片,图③是图②的示意图.已知,,.当与形成的为时,求的长.(参考数据:,,;,,
【变式2-4】(2024•杨浦区三模)如图1是光的反射规律示意图,是入射光线,是反射光线,法线平面镜,入射角等于反射角.
如图2,水平桌面上从左至右分别竖直放置了挡板、挡板、平面镜,在挡板的正上方有一可上下移动的挡板(挡板的厚度都忽略不计).已知厘米,当从点发出的光线经平面镜反射后恰好经过点时,测得入射角为.(参考数据:,
(1)点到平面镜的距离是 厘米.
(2)移动挡板,使空隙的长度是20厘米,当从点发出的光线经平面镜反射后恰好经过点时,求入射角的度数.
(3)在(2)的条件下,如果从点发出的光线经平面镜反射后通过空隙落到挡板上的最高点为,最低点为,那么的长度是 厘米.
【变式2-5】(2023•奉贤区三模)如图1,是一种购物小拉车,底部两侧装有轴承三角轮,可以在平路及楼梯上推拉物品.拉杆固定在轴上,可以绕连接点旋转,拉杆,置物板,脚架形状保持不变.图2,图3为购物车侧面示意图,拉杆,,,,,的半径均为,为三角轮的中心,,.如图2,当轮子,及点都放置在水平地面时,恰好与的最高点重合.此时,的高度为,则 ;如图3,拉动,使轮子,在楼梯表面滚动,当,且,,三点共线时,点与的垂直高度差为 .
【考点题型三】解直角三角形的应用-坡度坡角问题(共7小题)
【例3】(2024•徐汇区二模)小杰沿着坡比的斜坡,从坡底向上步行了130米,那么他上升的高度是 米.
【变式3-1】(2023秋•杨浦区期末)小华沿着坡度的斜坡向上行走了米,那么他距离地面的垂直高度上升了 米.
【变式3-2】(2024•徐汇区三模)一斜坡的坡角为,坡长比坡高多100米,那么斜坡的高为 (用的锐角三角比表示).
【变式3-3】(2022秋•崇明区期末)如图,有一斜坡长,坡顶离地面的高度为,求的长度及此斜坡的倾斜角的度数.
【变式3-4】(2024•宝山区二模)小明家院内靠墙安装了一个遮阳篷(如图,图2是它的侧面示意图,遮阳篷长米,与水平面的夹角为,靠墙端离地高度米,已知该地区冬至正午太阳光照入射角,夏至正午太阳光照入射角,因此,点、之间的区域是一年四季中阳光不一定照射到的区域,求该区域深度的长.(结果精确到0.1米)
参考数据:,,;,,;,,.
【变式3-5】(2023•奉贤区二模)图是某地下商业街的入口的玻璃顶,它是由立柱、斜杆、支撑杆组成的支架撑起的,它的示意图.经过测量,支架的立柱与地面垂直,米,点、、在同一水平线上,斜杆与水平线的夹角,支撑杆,垂足为,该支架的边与的夹角,又测得米.
(1)求该支架的边的长;
(2)求支架的边的顶端到地面的距离.(结果精确到0.1米)
(参考数据:,,,,,
【变式3-6】(2022秋•静安区期末)有一把长为6米的梯子,将它的上端靠着墙面,下端放在地面上,梯子与地面所成的角记为,地面与墙面互相垂直(如图1所示).一般满足时,人才能安全地使用这架梯子.
(1)当梯子底端距离墙面2.5米时,求的度数(结果取整数),此时人是否能安全地使用这架梯子?
(2)当人能安全地使用这架梯子,且梯子顶端离开地面最高时,梯子开始下滑,如果梯子顶端沿着墙面下滑1.5米到墙面上的点处停止,梯子底端也随之向后平移到地面上的点处(如图2所示),此时人是否能安全使用这架梯子?请说明理由.
【考点题型四】解直角三角形的应用-仰角俯角问题(共6小题)
【例4】(2023秋•徐汇区期末)世博会期间,从一架离地200米的无人机上,测得地面监测点的俯角是,那么此时无人机与地面监测点的距离是
A.米B.米C.200米D.米
【变式4-1】(2024•浦东新区校级开学)某人在高为15米的建筑物顶部测得地面一观察点的俯角为,那么这个观察点到建筑物的距离为 .
【变式4-2】(2024•青浦区二模)如图,热气球的探测器显示,从热气球处看一栋楼顶部的仰角为,看这栋楼底部的俯角为,热气球处与楼的水平距离为米,那么这栋楼的高度为
米.(用含、、的式子表示)
【变式4-3】(2024•徐汇区校级三模)社团活动课上,九年级学习小组测量学校旗杆的高度.如图,他们在处测得旗杆顶部的仰角为,,则旗杆的高度为 .
【变式4-4】(2023秋•徐汇区期末)小杰在学习了“仰角、俯角、坡比”后,他在自己居住的小区设计了如下测量方案:小杰利用小区中的一个斜坡,首先在斜坡的底端测得高楼顶端的仰角是,然后沿斜坡向上走到处,再测得高楼顶端的仰角是,已知斜坡的坡比是,斜坡的底端到高楼底端的距离是米,且、、三点在一直线上(如图所示).假设测角仪器的高度忽略不计,请根据小杰的方案,完成下列问题:
(1)求高楼的高度;
(2)求点离地面的距离(结果精确到0.1米).
(参考数据:,,,
【变式4-5】(2023秋•普陀区期末)如图,小河的对岸有一座小山,小明和同学们想知道山坡的坡度,但由于山坡前有小河阻碍,无法直接从山脚处测得山顶的仰角,于是小明和同学们展开了如下的测量:
第一步:从小河边的处测得山顶的仰角为;
第二步:从处后退30米,在处测得山顶的仰角为;
第三步:测得小河宽为33米.
已知点、、在同一水平线上,请根据小明测量的数据求山坡的坡度.
(参考数据:,,,,,
【考点题型五】解直角三角形的应用-方向角问题(共6小题)
【例5】(2023秋•金山区期末)如图,为了绕开岛礁区,一艘船从处向北偏东的方向行驶8海里到处,再从处向南偏东方向行驶到发点正东方向上的处,此时这艘船距离出发点处 海里.
【变式5-1】(2023秋•嘉定区期末)如图,在港口的南偏西方向有一座小岛,一艘船以每小时12海里的速度从港口出发,沿正西方向行驶,行了30分钟时这艘船在处测得小岛在船的正南方向,那么小岛与处的距离 海里(结果保留根号).
【变式5-2】(2023秋•徐汇区期末)如图,一段东西向的限速公路长500米,在此公路的南面有一监测点,从监测点观察,限速公路的端点在监测点的北偏西方向,端点在监测点的东北方向,那么监测点到限速公路的距离是 米(结果保留根号).
【变式5-3】(2024•普陀区校级三模)在城市地气象台测得台风中心在该地正西方向300千米的处正以每小时26千米的速度沿射线(北偏东方向)移动,如果距台风中心200千米范围内是受台风影响的区域.假如这次台风从点位置沿北偏东方向移动3小时后,方向转为北偏东方向继续行进.
请问:城市是否受到台风的影响?如果受到影响,请计算影响的时间;如果不影响,请说明理由?(结果保留一位小数,参考数据:
【变式5-4】(2022秋•崇明区期末)如图,航母由西向东航行,到达处时,测得小岛位于它的北偏东方向,且与航母相距80海里,再航行一段时间后到达处,测得小岛位于它的北偏东方向,如果航母继续航行至小岛的正南方向的处,求还需航行的距离的长.参考数据:,,
【变式5-5】(2024•嘉定区二模)某东西方向的海岸线上有、两个码头,这两个码头相距60千米,有一艘船在这两个码头附近航行.
(1)当船航行了某一刻时,由码头测得船在北偏东,由码头测得船在北偏西,如图1,求码头与船的距离的长),其结果保留3位有效数字;
(参考数据:,,,
(2)当船继续航行了一段时间时,由码头测得船在北偏东,由码头测得船在北偏西,船到海岸线的距离是(即,如图2,求的长,其结果保留根号.
清单04 图形的相似(11个考点梳理+题型解读+提升训练)-2024-2025学年九年级数学上学期期中考点大串讲(北师大版)(解析版): 这是一份清单04 图形的相似(11个考点梳理+题型解读+提升训练)-2024-2025学年九年级数学上学期期中考点大串讲(北师大版)(解析版),共40页。
清单03 概率投影和视图(8个考点梳理+题型解读+提升训练)-2024-2025学年九年级数学上学期期中考点大串讲(北师大版)(解析版): 这是一份清单03 概率投影和视图(8个考点梳理+题型解读+提升训练)-2024-2025学年九年级数学上学期期中考点大串讲(北师大版)(解析版),共35页。
专题02 有理数的运算(考点清单,知识导图+10个考点清单+6种题型解读)-2024-2025学年七年级数学上学期期中考点练习(人教版2024).zip: 这是一份专题02 有理数的运算(考点清单,知识导图+10个考点清单+6种题型解读)-2024-2025学年七年级数学上学期期中考点练习(人教版2024).zip,文件包含专题02有理数的运算考点清单知识导图+10个考点清单+6种题型解读原卷版docx、专题02有理数的运算考点清单知识导图+10个考点清单+6种题型解读解析版docx等2份试卷配套教学资源,其中试卷共38页, 欢迎下载使用。












