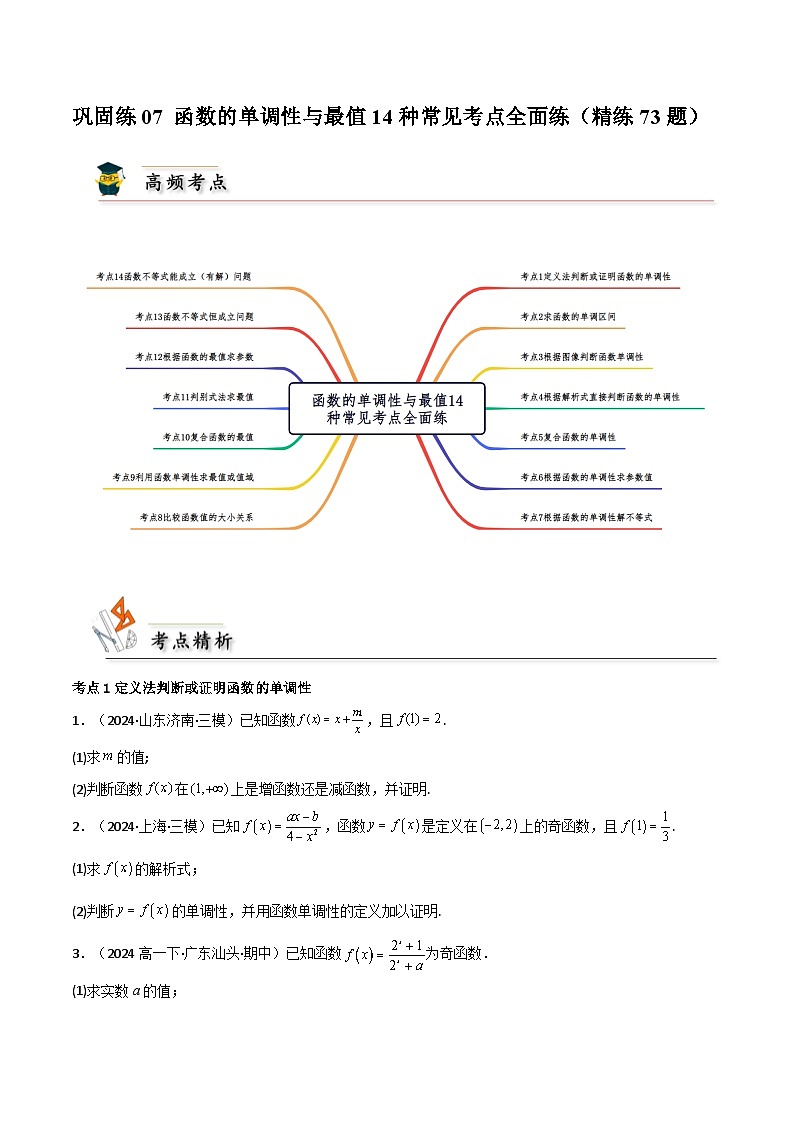




所属成套资源:备战2025年高考数学一轮复习综合练习
备战2025年高考数学一轮复习综合练习——函数的单调性与最值
展开
这是一份备战2025年高考数学一轮复习综合练习——函数的单调性与最值,文件包含巩固练07函数的单调性与最值14种常见考点全面练精练73题原卷版docx、巩固练07函数的单调性与最值14种常见考点全面练精练73题解析版docx等2份试卷配套教学资源,其中试卷共60页, 欢迎下载使用。
考点1定义法判断或证明函数的单调性
1.(2024·山东济南·三模)已知函数,且.
(1)求的值;
(2)判断函数在上是增函数还是减函数,并证明.
【答案】(1)1
(2)增函数,证明见解析
【分析】(1)将代入函数求值即可;
(2)利用单调性的定义判断即可.
【详解】(1),
(2)函数为增函数,证明如下:
设是1,+∞上的任意两个实数,且,
则
当时,,,
从而,即,
∴函数在1,+∞上为增函数.
2.(2024·上海·三模)已知,函数是定义在上的奇函数,且.
(1)求的解析式;
(2)判断的单调性,并用函数单调性的定义加以证明.
【答案】(1)
(2)在区间上为严格增函数,证明见解析
【分析】(1)根据题意,由奇函数的性质可得,求出的值,结合函数的解析式求出的值,计算可得答案;
(2)根据题意,根据单调性的定义,结合作差法证明可得答案.
【详解】(1)根据题意,是定义在上的奇函数,
则有,解得,
又由,解得,
所以,定义域为,
且,所以;
(2)在区间上为严格增函数.
证明如下:设任意,则,
由,得,
即,,,
所以,即,
故在区间上为严格增函数.
3.(2024高一下·广东汕头·期中)已知函数为奇函数.
(1)求实数a的值;
(2)判断函数的单调性(不用证明);
(3)设函数,若对任意的,总存在,使得成立,求实数m的取值范围.
【答案】(1)
(2)在,上单调递减.
(3)
【分析】(1)考虑和两种情况,根据奇函数性质计算得到答案.
(2)确定定义域,设,且,计算,得到单调性.
(3)根据单调性确定时的值域,设,换元得到二次函数,计算最大值和最小值,根据值域的包含关系得到答案.
【详解】(1)由已知函数需满足,当时,函数的定义域为,
函数为奇函数,所以f−x=−fx,
即在上恒成立,即,(舍),
当时,,函数的定义域为,
又函数为奇函数,所以,
此时,函数定义域为,
,函数为奇函数,满足,
综上所述:;
(2)在和0,+∞上单调递减,证明如下:
,定义域为,
设,且,
则
因为,且,所以,
所以,所以在0,+∞上单调递减,
同理可证,所以在上单调递减;
所以在0,+∞,上单调递减.
(3)函数在和0,+∞上单调递减,
且当时,,当x∈0,+∞时,,
时,,所以当时的值域,
又,
设,则,
当时,取最小值为,当时,取最大值为,
即在上的值域,
又对任意的,总存在,使得成立,
即,所以,解得,即.
4.(2024高二下·陕西西安·阶段练习)已知奇函数的定义域为.
(1)求实数的值;
(2)判断函数的单调性,并用定义证明;
(3)存在,使得成立,求实数m的取值范围.
【答案】(1);
(2)单调递增,证明见解析;
(3).
【分析】(1)根据函数是奇函数,由求得,再根据定义域关于原点对称求解;
(2)利用定义法证明函数的单调性;
(3)存在,使得恒成立,令,,转化为,存在时成立求解.
【详解】(1)因为函数是奇函数,所以,即,则,整理可得,所以,
又因为定义域关于原点对称,所以,即,
所以;
(2)在上单调递增,
设任意,且,
则,
因为,所以,
又,,
所以,即,
所以在上单调递增;
(3)因为,所以,
由存在,使得成立,
则,存在时成立,
令,,
则,存在时成立,
构造函数,
故,
而,当且仅当,即取等号,
对于单调递减,在单调递增,
所以,,
所以,
∴
故的取值范围为.
考点2求函数的单调区间
5.(2024·湖南岳阳·模拟预测)已知函数,则下列结论错误的是( )
A.B.的零点为3
C.在上为增函数D.的定义域为
【答案】C
【分析】由函数性质依次判断各选项可得出结果.
【详解】,可知函数的零点为3,可知A,B正确;
中,由,解得:,
故函数的定义域为,且函数在为增函数,故C错误,D正确.
故选:C
6.(2024·江西·二模)已知函数若,则的单调递增区间为( )
A.B.
C.D.
【答案】D
【分析】先根据题目条件求出 的值,再根据二次函数的性质求出 的单调递增区间
【详解】解:依题意,解得a=-1,故,可知在上单调递增
故选:D
7.(2024·全国·模拟预测)已知函数,则( )
A.在单调递增B.在单调递减
C.的图象关于直线对称D.的图象关于点对称
【答案】C
【分析】首先求函数的定义域,再化简函数,分析内层函数的单调性和对称性,从而判断选项.
【详解】函数的定义域满足 ,即,
即函数的定义域是,
,
设,
由复合函数单调性可知函数在单调递增,在单调递减,故AB不正确;
,,
所以,函数关于直线对称.
故选:C
【点睛】本题考查函数的单调性和对称性,重点考察转化与化归的思想,复合函数判断函数性质的方法,属于基础题型。
8.(2024·广东深圳·三模)函数的单调递增区间是 .
【答案】
【分析】作出函数的图象,根据图象即可求出结果.
【详解】函数,
由,解得或,
函数的图象如图所示,
由图可知,函数的单调递增区间为.
故答案为:.
9.(2024·全国·三模)函数的单调递减区间为 .
【答案】
【分析】利用导数求出的单调区间,从而可求出函数的减区间
【详解】当时,,则其在上递减,
当时,,则,
当时,,所以在上递减,
综上,的单调递减区间为,
故答案为:
考点3根据图像判断函数单调性
10.(2024高一上·福建泉州·阶段练习)如图所示是函数的图象,图中曲线与直线无限接近但是永不相交,则以下描述正确的是( )
A.函数的定义域为
B.函数的值域为
C.此函数在定义域中不单调
D.对于任意的,都有唯一的自变量x与之对应
【答案】C
【分析】由函数图象确定定义域和值域,单调性判断各项的正误.
【详解】由图知:的定义域为,值域为,A、B错;
显然在分别递增,但在定义域上不单调,C对;
显然,对应自变量x不唯一,D错.
故选:C
11.(2024·辽宁丹东·二模)设函数由关系式确定,函数,则( )
A.为增函数B.为奇函数
C.值域为D.函数没有正零点
【答案】D
【分析】化简已知函数并作出图像,即可得出结论
【详解】由题意,
在函数中,,
可知画以下曲线:
,,.
这些曲线合并组成图象,是两段以为渐近线的双曲线和一段圆弧构成.
因为作图象在轴右侧部分包括点关于x轴对称,
得到曲线,再作关于坐标原点对称,去掉点得到曲线,与合并组成图象.
由图象可知,不是奇函数,不是增函数,值域为R.
当时,图象与图象没有公共点,从而函数没有正零点.
故选:D.
12.(2024·贵州·模拟预测)已知函数,下列结论正确的是( )
A.是偶函数
B.在上单调递增
C.的图象关于直线对称
D.的图象与轴围成的三角形面积为2
【答案】C
【分析】去掉绝对值,得到,画出其图象,进而判断出四个选项.
【详解】A选项,,
画出其函数图象,如下:
故不是偶函数,A错误;
B选项,在上单调递减,故B错误;
C选项,的图象关于直线对称,C正确;
D选项,的图象与轴围成的三角形面积为,D错误.
故选:C
13.(2024高三上·广西·学业考试)在2小时内将某种药物注射进患者的血液中,在注射期间,血液中的药物含量呈线性增加;停止注射后,血液中药物含量呈指数衰减,能反映血液中药物含量Q随时间t变化的图象是( )
A. B. C. D.
【答案】C
【分析】根据题意结合单调性判断.
【详解】根据题意函数先递增再递减,进而判断C选项符合题意.
故选:C.
考点4根据解析式直接判断函数的单调性
14.(24-25高一上·全国·随堂练习)函数在上的最小值为( )
A.1B.C.D.
【答案】B
【分析】根据题意可知函数在上单调递减,结合单调性求最值.
【详解】因为在上单调递增,且恒成立,
可知函数在上单调递减,
当时,,所以函数在上的最小值为.
故选:B.
15.(24-25高三上·甘肃天水·阶段练习)下列函数中,是偶函数且在上单调递减的是( )
A.B.
C.D.
【答案】D
【分析】先检验函数的定义域是否关于原点对称,再考查是否为偶函数,结合函数解析式,分析函数在0,+∞上的单调性即得.
【详解】对于A,因,则函数为偶函数,
且显然在0,+∞上先减后增,故A错误;
对于B,因,则函数为偶函数,且,
显然函数在0,+∞上为增函数,故B错误;
对于C,函数的定义域为0,+∞,故是非奇非偶函数,故C错误;
对于D,因的定义域为,关于原点对称,
且,即函数是偶函数,且在0,+∞上单调递减,即D正确.
故选:D.
16.(2024高一上·北京·期中)下列函数中,在区间上是减函数的是( )
A.B.
C.D.
【答案】D
【分析】利用函数解析式直接判断各选项中的函数单调性即得.
【详解】函数、在R上单调递增,AB不是;
函数在上单调递增,C不是;
函数在上单调递减,D是.
故选:D
17.(2024高二下·云南·学业考试)下列函数中,在上单调递增的是( )
A.B.
C.D.
【答案】C
【分析】根据函数解析式直接判断函数单调性即可.
【详解】对于选项A:因为在上单调递减,故A错误;
对于选项B:因为在上单调递减,故B错误;
对于选项C:因为在上单调递增,故C正确;
对于选项D:因为在内单调递减,在上单调递增,故D错误;
故选:C.
考点5复合函数的单调性
18.(2024高三·全国·专题练习)函数的单调递增区间为( )
A.B.C.D.
【答案】C
【分析】先求出函数的定义域,再根据二次函数及复合函数的性质求解即可.
【详解】由题意可得,即,解得或,
令(或),则,
因为的对称轴为,
所以在上递减,在上递增,
因为在定义域内递增,
所以在上递减,在上递增.
故选:C
19.(2024高一上·全国·课后作业)函数的单调递增区间为( )
A.B.
C.D.
【答案】B
【分析】先求函数的定义域,在结合复合函数单调性分析求解.
【详解】令,解得,
所以函数的定义域为,
因为开口向下,对称轴为,
可知在上单调递增,在上单调递减,
且在定义域内单调递增,
所以在上单调递增,在上单调递减,
又因为在定义域内单调递增,
所以在上单调递增,在上单调递减,
即函数的单调递增区间为.
故选:B.
20.(2024高三上·广东湛江·开学考试)已知函数,则的增区间为( )
A.B.C.D.
【答案】A
【分析】利用复合函数的单调性求函数的增区间.
【详解】函数定义域为,
令,又在上单调递增,的增区间为,
所以的增区间为.
故选:A.
21.(2024高一上·北京·阶段练习)函数单调递增的区间是 .
【答案】
【分析】把已知函数解析式变形,再由正弦型函数的单调性求解即可.
【详解】解:函数,
则函数在上的单增区间满足:,,
解得,.
函数单调递增的区间是.
故答案为:.
考点6根据函数的单调性求参数值
22.(2024·广东揭阳·二模)已知函数在上不单调,则的取值范围为( )
A.B.
C.D.
【答案】C
【分析】根据给定条件,利用二次函数的单调性列出不等式求解即得.
【详解】函数的图象对称轴为,依题意,,得,
所以的取值范围为.
故选:C
23.(2024·天津河北·一模)设,则“”是“函数在上单调递增”的( )
A.充分不必要条件B.必要不充分条件
C.充要条件D.既不充分也不必要条件
【答案】A
【分析】根据题意,由二次函数的对称轴和函数的单调性的关系以及充分性与必要性的应用,即可得到结果.
【详解】函数的对称轴为,
由函数在上单调递增可得,即,
所以“”是“函数在上单调递增”的充分不必要条件.
故选:A
24.(2024·山东·二模)已知函数在区间上单调递增,则的取值范围是( ).
A.7,+∞B.
C.D.
【答案】A
【分析】根据题意,结合二次函数的性质,求得解得,再由,进而求得的取值范围.
【详解】由函数的对称轴是,
因为函数在区间上是增函数,所以,解得,
又因为,因此,所以的取值范围是7,+∞.
故选:A.
25.(2024·黑龙江·模拟预测)设函数在区间上单调递减,则的取值范围是( )
A.B.C.D.
【答案】D
【分析】由复合函数的单调性分析得在上单调递减,根据单调性即可得到答案.
【详解】设,易知函数是增函数,
因为在区间上单调递减,
所以由复合函数单调性可知,在上单调递减.
因为函数在上单调递减,
所以,即.
故选:D.
26.(2024·黑龙江哈尔滨·模拟预测)若函数在上单调递增,则实数的取值范围为( )
A.B.C.D.
【答案】A
【分析】根据条件得即在上恒成立,构造函数,,由二次函数的性质求出的最值即可解决问题.
【详解】因为函数在上单调递增,
所以在上恒成立,即在上恒成立,
令,,变形得,因为,所以,
所以当,即时,,所以.
故选:A.
27.(2024·陕西榆林·一模)已知函数在上单调递增,则的取值范围是( )
A.B.C.D.
【答案】B
【分析】分情况讨论,当时直接代入可得函数递减;当时,求导,构造函数,,再由得到抽象函数,求出,最后再讨论时的情况,综合得出结果.
【详解】当时,函数在上单调递减,不符合题意,所以,
由题可知恒成立,即.令,
则,所以在上单调递增,由,
可得,即,所以,所以,
当时,,不符合题意,故的取值范围是.
故选:B
28.(2024·陕西安康·模拟预测)已知函数是上的单调函数,则实数的取值范围是( )
A.B.C.D.
【答案】B
【分析】根据题意,结合分段函数的单调性的判定方法,结合对数函数的性质,列出关于的不等式,即可求解.
【详解】根据题意,当时,,可得在上递增,
要使得函数 是上的单调函数,
则满足,且,解可得,
所以实数的取值范围为.
故选:B.
29.(2024·江苏无锡·二模)已知函数满足对任意的,都有成立,则实数的取值范围为 .
【答案】
【分析】运用分段函数单调性知识,结合一次函数和指数型函数单调性知识可解.
【详解】由题意,为定义在上的减函数,则各段为减函数,还要区间端点附近递减,
所以,解得,则.
故答案为:.
30.(2024·辽宁·三模)已知函数存在两个极值点,若对任意满足的,均有,则实数的取值范围为( )
A.B.
C.D.
【答案】C
【分析】求出函数的导数,由导函数的两个零点求出的单调区间,求出所在区间,再由已知可得在同一单调递增区间内,进而求得,然后借助对勾函数单调性求出的范围.
【详解】函数的定义域为,求导得,
由函数存在两个极值点,得,即有两个不等的正根,
则,解得,当或时,,当时,,
于是函数在上单调递增,在上单调递减,
令,,则直线与的图象有3个公共点,
此时,显然,令,求导得,
即函数在上递增,则,即,于是,
由,得,
因为对任意满足的,均有,
则有必在同一单调递增区间内,因此,而恒成立,从而,
又,则,显然函数在上单调递增,
而,因此,由,得,
而函数在上单调递减,则,即,
所以实数的取值范围为.
故选:C
【点睛】关键点点睛:解决本题的关键是求出所在区间,由已知探讨得在同一单调递增区间内,再求出极小值点的范围.
考点7根据函数的单调性解不等式
31.(2024高三下·山西·阶段练习)已知函数fx=lg2x,02,若fa+1−f2a−1≥0,则实数a的取值范围是( )
A.B.C.D.
【答案】D
【分析】先求解函数的单调性,接着根据已知条件结合函数定义域和单调性即可求解.
【详解】因为当x∈0,2时,fx=lg2x是单调递增函数,此时fx≤f2=1,
当x∈2,+∞时,fx=2x−3是单调递增函数,此时fx>f2=1,
所以fx=lg2x,02是定义在0,+∞上的单调递增函数,
所以若fa+1−f2a−1≥0即fa+1≥f2a−1,
则a+1≥2a−1>0,⇒12
相关试卷
这是一份高考数学一轮复习 考点热身训练 2.2函数的单调性与最值,共5页。试卷主要包含了2函数的单调性与最值,已知函数f=,等内容,欢迎下载使用。
这是一份专题3.2 函数的单调性与最值(讲+练)-备战高考数学大一轮复习核心考点精讲精练(新高考专用),文件包含专题32函数的单调性与最值原卷版docx、专题32函数的单调性与最值解析版docx等2份试卷配套教学资源,其中试卷共43页, 欢迎下载使用。
这是一份备战2024年高考数学大一轮复习(人教A版-理)第二章 §2.2 函数的单调性与最值,共11页。试卷主要包含了掌握函数单调性的简单应用.等内容,欢迎下载使用。









