数学九年级上册3.6 圆内接四边形优秀ppt课件

这是一份数学九年级上册3.6 圆内接四边形优秀ppt课件，文件包含浙教版数学九上36《圆内接四边形》课件pptx、浙教版数学九上36《圆内接四边形》教学设计doc等2份课件配套教学资源，其中PPT共32页， 欢迎下载使用。

1.理解圆内接四边形和四边形的外接圆的概念.2.掌握圆内接四边形的性质，并会用此性质进行有关的计算和证明.3.通过对圆内接四边形的性质的探究，培养逻辑思维能力、分析问题和解决问题的能力，通过一题多解、一题多变进一步提高应用能力和思维能力.
顶点在圆上，并且两边都与圆相交的角.（二者必须同时具备）.
一条弧所对的圆周角等于它所对的圆心角的一半.
半圆（或直径）所对的圆周角是直角，90°的圆周角所对的弦是直径.
同弧或等弧所对的圆周角相等.
怎样把圆柱形原木锯成截面为正方形的木材，并使截面正方形的面积尽可能地大？
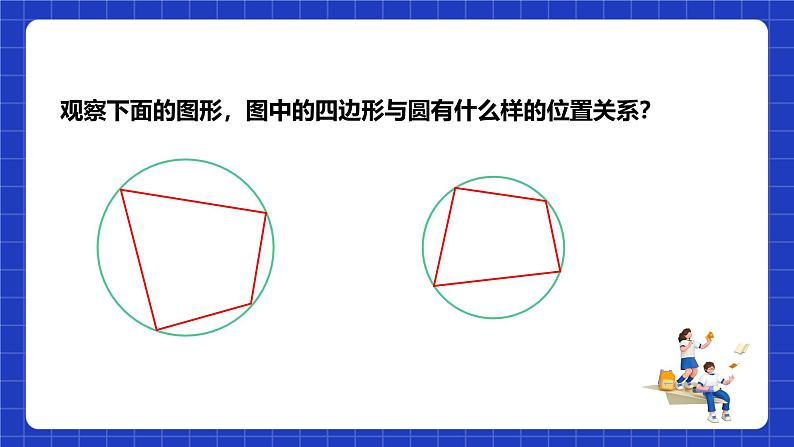
观察下面的图形，图中的四边形与圆有什么样的位置关系？
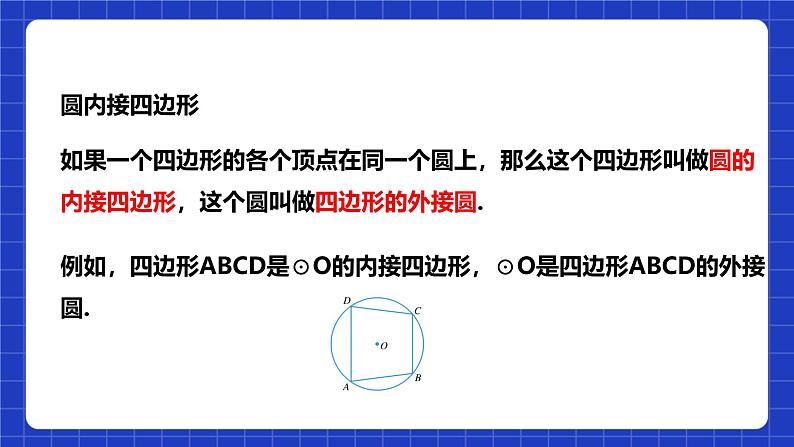
例如，四边形ABCD是⊙O的内接四边形，⊙O是四边形ABCD的外接圆.
如果一个四边形的各个顶点在同一个圆上，那么这个四边形叫做圆的内接四边形，这个圆叫做四边形的外接圆.
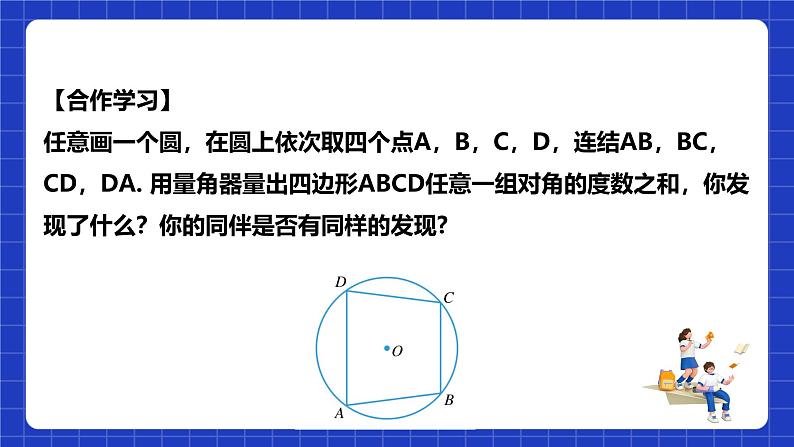
【合作学习】任意画一个圆，在圆上依次取四个点A，B，C，D，连结AB，BC，CD，DA. 用量角器量出四边形ABCD任意一组对角的度数之和，你发现了什么？你的同伴是否有同样的发现?
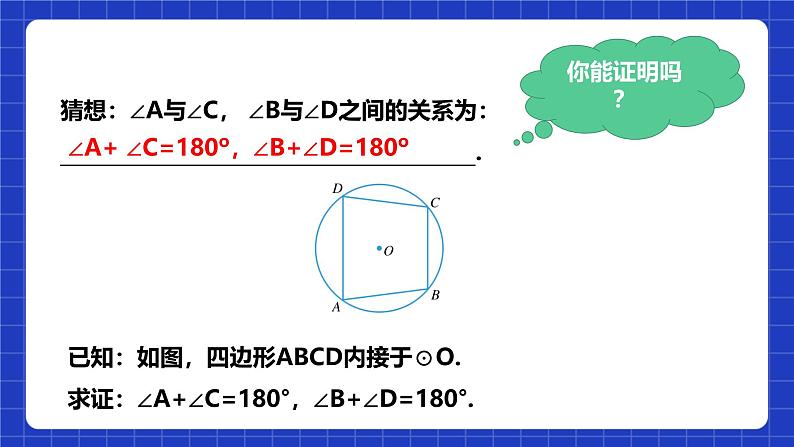
∠A+ ∠C=180º，∠B+∠D=180º
猜想：∠A与∠C， ∠B与∠D之间的关系为：________________________________________.
已知：如图，四边形ABCD内接于⊙O.求证：∠A+∠C=180°，∠B+∠D=180°.
你还有其他的证明方法吗？
圆内接四边形的性质定理:
圆内接四边形的对角互补.
符号语言：∵四边形ABCD内接于⊙O.∴∠A+∠C=180°，∠B+∠D=180°.
例1 已知：如图，AD是△ABC的外角∠EAC的平分线，与△ABC的外接圆交于点D. 求证：DB=DC.
分析：要证明DB=DC，只需证明∠DBC=∠DCB.根据“在同圆中，同弧所对的圆周角相等”,得∠DBC=∠DAC. 又根据“圆内接四边形的对角互补”和“同角的补角相等”,可得∠DCB=∠DAE.而已知∠DAC=∠DAE，这就证明了∠DBC=∠DCB.
证明：∵AD是∠EAC的平分线，∴∠DAC=∠DAE.∵四边形ABCD内接于圆，∴∠BAD+ ∠DCB=180°(圆内接四边形的对角互补).∴∠DCB=∠DAE.而∠DAC=∠DBC(在同圆中,同弧所对的圆周角相等)∴∠DCB=∠DBC，∴DB=DC.
【例2】如果要把直径为30cm的圆柱形原木锯成一根横截面为正方形的木材，并使截面尽可能地大，应怎样锯？如果这根原木长15m，问锯出的木材的体积为多少立方米(树皮等损耗略去不计)?
解：设原木的横截面为⊙O.要使锯出的木材的横截面正方形ABCD尽可能地大，正方形ABCD应内接于⊙O.由正方形ABCD四个内角都是直角，得它的两条对角线是⊙O的两条直径，且这两条直径互相垂直.所以只要在⊙O内作两条互相垂直的直径AC和BD，就可以作出⊙O的内接正方形ABCD.
【知识技能类作业】 必做题：1.如图所示，四边形ABCD为 ⊙O 的内接四边形，∠BCD=120°，则∠BOD的大小是( )A.80° B.120°C.100°D.90°
2.如图，在圆内接四边形ABCD中，若∠A，∠B，∠C的度数之比为4∶3∶5，则∠D的度数是______°.
3.如图,四边形ABCD内接于⊙O，点E在BC的延长线上，若∠BOD＝120°，求∠DCE的度数。
4.如图，四边形ABCD为⊙O的内接四边形.AB与DC的延长线交于点G，AO⊥CD，垂足为E，连接BD，∠GBC=50° ，则∠DBC的度数为( )°B.60°C.80°D.90°
【知识技能类作业】 选做题：5.如图，四边形 ABCD 是圆 O 的内接四边形，点 D 是 AC的中点，点 E 是 BC上的一点，若 ∠CED=40°，则∠ADC=_____度 .
6.如图，四边形ABCD内接于⊙O，四边形ABCO是平行四边形，则∠ADC的度数为( )°B.50° C.60° D.75°
7.如图所示，四边形ABCD内接于⊙O，∠B＝50°，∠ACD＝25°，∠BAD＝65°.求证：(1)AD＝CD；
证明：∵四边形ABCD内接于⊙O，∴∠D=180°-∠B=130°.∵∠ACD=25°，∴∠DAC=180°-∠D-∠ACD=25°，∴∠DAC=∠ACD，∴AD=CD.
7.如图所示，四边形ABCD内接于⊙O，∠B＝50°，∠ACD＝25°，∠BAD＝65°.求证：(2)AB是⊙O的直径．
证明：∵∠BAC=∠BAD-∠DAC=65°-25°=40°，∠B=50°，∴∠ACB=180°-∠B-∠BAC＝90°，∴AB是⊙O的直径．
本节课你学到了哪些知识？
1.如果一个四边形的各个顶点在同一个圆上，那么这个四边形叫做圆的内接四边形，这个圆叫做四边形的外接圆.2.圆内接四边形的性质定理：圆内接四边形的对角互补.
【知识技能类作业】必做题
1.如图，四边形ABCD内接于⊙O.若∠B＝72°，则∠D的度数为(　　).A．18°　　B．72°　　C．100°　　D．108°
2.如图，四边形ABCD内接于⊙O，E为CD延长线上一点．若∠B＝110°，则∠ADE＝(　　 ).A．35° B．55° C．70° D．110°
选做题：3.如图，四边形ABCD是⊙O的内接四边形，BE是⊙O的直径，连结AE.若∠BCD＝2∠BAD，则∠DAE的度数是(　　).A．30° B．35° C．45° D．60°
4.如图，四边形ABDE是⊙O的内接四边形，CE是⊙O的直径，连结BC，DC.若∠BDC＝20°，则∠A的度数为(　　).A．90° B．100° C．110° D．120°
【综合实践类作业】5.如图，在△ABC中，AB＝AC，以AB为直径的半圆O分别交AC，BC于点D，E.(1)求证：点E是BC的中点；
证明：如图，连结AE.∵AB为直径，∴∠AEB＝90°，即AE⊥BC.又∵AB＝AC，∴BE＝CE，即点E为BC的中点．
【综合实践类作业】5.如图，在△ABC中，AB＝AC，以AB为直径的半圆O分别交AC，BC于点D，E.(2)若∠BOD＝75°，求∠CED的度数.