






所属成套资源:浙教版数学九上课件PPT+教案整册(含单元教案)
浙教版(2024)九年级上册4.3 相似三角形获奖课件ppt
展开
这是一份浙教版(2024)九年级上册4.3 相似三角形获奖课件ppt,文件包含浙教版数学九上451《相似三角形的性质》课件pptx、浙教版数学九上451《相似三角形的性质》教学设计doc等2份课件配套教学资源,其中PPT共26页, 欢迎下载使用。
1.进一步理解相似比的概念,掌握相似三角形的性质定理.2.掌握综合运用相似三角形的判定定理和性质定理来解决问题.3.通过相似性质的学习,感受图形和语言的和谐美,进一步培养类比的教学思想.
【想一想】我们已经学过哪些判定三角形相似的方法?
方法1:两角分别相等的两个三角形相似。
方法2:两边成比例且夹角相等的两个三角形相似。
方法3:三边对应成比例的两个三角形相似。
根据相似三角形的定义,我们可得到相似三角形的两个基本性质:
相似三角形的对应角相等,对应边成比例.
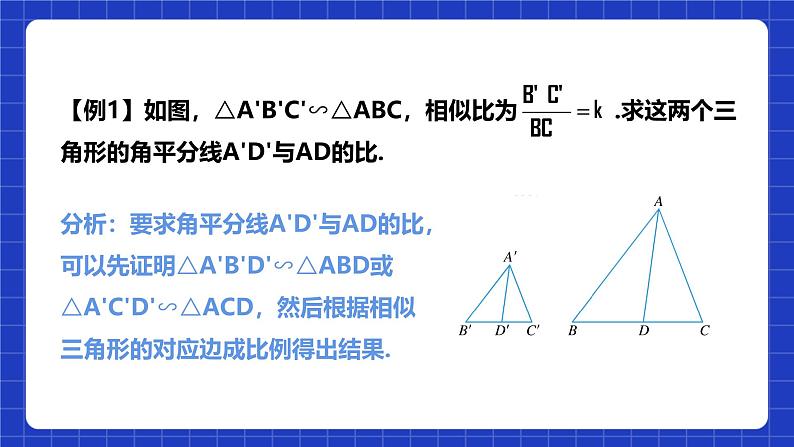
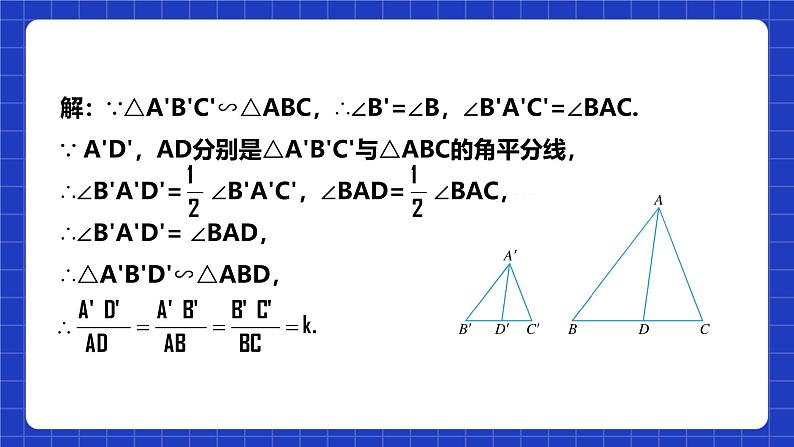
分析:要求角平分线A'D'与AD的比,可以先证明△A'B'D'∽△ABD或△A'C'D'∽△ACD,然后根据相似三角形的对应边成比例得出结果.
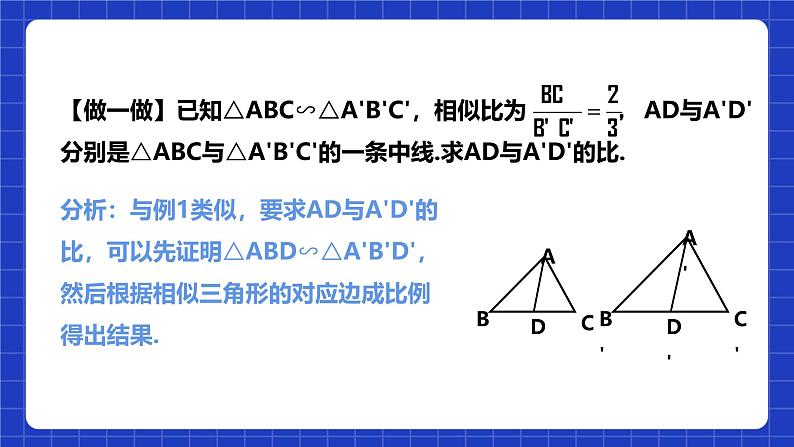
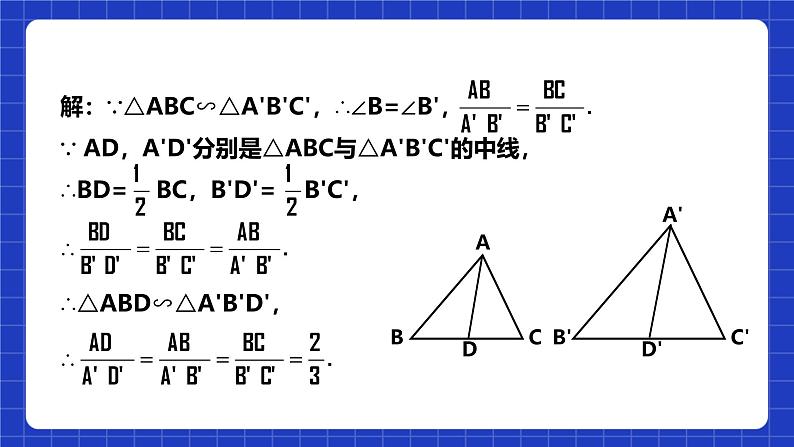
分析:与例1类似,要求AD与A'D'的比,可以先证明△ABD∽△A'B'D',然后根据相似三角形的对应边成比例得出结果.
相似三角形对应高的比、对应角平分线的比、对应中线的比都等于相似比.
一般的,我们有:相似三角形对应线段的比等于相似比。
【例2】已知:如图,BD,CE是△ABC的两条中线,P是它们的交点.求证:
例2中,如果再作BC边上的中线,这条中线与AC边上的中线BD的交点也必定分BD成1:2的两条线段,也就是点P.这就证明了三角形的三条中线相交于一点.
三角形三条中线的交点叫做三角形的重心.
三角形的重心分每一条中线成1:2的两条线段.
【知识技能类作业】 必做题:1.(1)两个相似三角形的相似比为1:2, 则对应高的比为_________, 则对应中线的比为_________.(2)两个相似三角形对应中线的比为1:4 ,则对应高的比为______ .
2.△ABC 与△A'B'C' 的相似比为3 : 4,若 BC 边上的高 AD=12 cm,则 B'C'边上的高 A'D' 为( )cm.A. 3B. 4 C. 12D. 16
3.已知△ABC∽△DEF,BG、EH是△ABC和△DEF的角平分线,BC=6cm,EF=4cm,BG=4.8cm. 求EH的长.
4.下列说法正确的是( ).A.一条线段的黄金分割点有且只有一个B.三角形三条中线的交点叫做三角形的重心,三角形的重心到一个顶点的距离等于它到中点距离的两倍C.两边对应成比例且有一角对应相等的两个三角形相似D.相似三角形对应线段(对应角平分线、对应中线、对应高)的比等于相似比
【知识技能类作业】 选做题:5.在 △ABC 和 △DEF 中,AB=2 DE,AC=2 DF,∠A=∠D,AP,DQ 是中线,若 AP=2,则 DQ的值为( ).A.2 B.4 C.1 D . 3
6. 若△ABC∽△DEF,且对应高线比为4∶9,则△ABC与△DEF的相似比为( ).A.2∶3 B.3∶2C.4∶9 D.16∶81
【综合实践类作业】7.如图,在△ABC中,点D,E分别在AB,AC上,AF平分∠BAC,交DE于点G.如果AE=3,EC=1,AD=2,BD=4,求AF∶AG的值.
解:∵AE=3,EC=1,AD=2,BD=4,∴AC=4,AB=6.∴AB∶AE=AC∶AD=2.又∵∠BAC=∠EAD,∴△ABC∽△AED.又∵AF为△ABC的角平分线,AG为△AED的角平分线,∴AF∶AG=AC∶AD=2.
本节课你学到了哪些知识?
1.相似三角形对应高的比、对应角平分线的比、对应中线的比都等于相似比.2.相似三角形对应线段的比等于相似比.3.三角形三条中线的交点叫做三角形的重心.4.三角形的重心分每一条中线成1:2的两条线段.
【知识技能类作业】必做题
1.已知△ABC∽△A′B′C′,AD、A′D′是它们的对应角平分线,且AD=8cm,A′D′=3cm,则△ABC与△A′B′C′对应高的比为( ).A. 3:8B. 8∶3C. 1∶3D. 1∶8
2. 两个相似三角形的相似比为2∶5,已知其中一个三角形的一条中线为10,那么另一个三角形对应的中线为( ).A. 2B. 4或25C. 2或4D. 4
选做题:3.如图,在△ABC中,BC=120,高AD=60,正方形EFGH的一边在BC上,点E,F分别在AB,AC上,AD交EF于点N,则AN的长为( ).A.15 B.20 C.25 D.30
【综合实践类作业】4. 如图,在△ABC中,点D,E,F分别在AB,BC,AC上,DE∥AC,EF∥AB.(1)求证:△BDE∽△EFC.
证明:∵DE∥AC,∴∠DEB=∠FCE.∵EF∥AB,∴∠DBE=∠FEC.∴△BDE∽△EFC.
相关课件
这是一份数学九年级上册第4章 相似三角形4.5 相似三角形的性质及应用授课ppt课件,共24页。PPT课件主要包含了知识点,三角形的重心及其性质,三角形的角大小不变等内容,欢迎下载使用。
这是一份初中数学浙教版九年级上册4.3 相似三角形教学演示ppt课件,共25页。PPT课件主要包含了知识点,三角形的重心及其性质,三角形的角大小不变等内容,欢迎下载使用。
这是一份初中数学浙教版九年级上册第4章 相似三角形4.3 相似三角形优秀ppt课件,文件包含浙教版数学九上453相似三角形的性质及其应用课件pptx、浙教版数学九上453相似三角形的性质及其应用学案doc、浙教版数学九上453相似三角形的性质及其应用教案doc等3份课件配套教学资源,其中PPT共20页, 欢迎下载使用。










