中考数学总复习举一反三系列(通用版)专题06分式方程及其应用(10个高频考点)(原卷版+解析)

这是一份中考数学总复习举一反三系列(通用版)专题06分式方程及其应用(10个高频考点)(原卷版+解析)，共32页。
TOC \ "1-1" \h \u
\l "_Tc11773" 【考点1 分式方程的定义】 PAGEREF _Tc11773 \h 1
\l "_Tc31517" 【考点2 分式方程的解】 PAGEREF _Tc31517 \h 2
\l "_Tc4787" 【考点3 解分式方程】 PAGEREF _Tc4787 \h 2
\l "_Tc26689" 【考点4 换元法解分式方程】 PAGEREF _Tc26689 \h 3
\l "_Tc1809" 【考点5 分式方程的增根】 PAGEREF _Tc1809 \h 3
\l "_Tc12008" 【考点6 分式方程的无解】 PAGEREF _Tc12008 \h 4
\l "_Tc17027" 【考点7 不等式与分式方程的综合】 PAGEREF _Tc17027 \h 4
\l "_Tc24191" 【考点8 分式方程中的新定义问题】 PAGEREF _Tc24191 \h 5
\l "_Tc23951" 【考点9 由实际问题抽象出分式方程】 PAGEREF _Tc23951 \h 5
\l "_Tc8456" 【考点10 分式方程的应用】 PAGEREF _Tc8456 \h 6
【要点1 分式方程的定义】
分母中含有未知数的方程叫做分式方程。
【考点1 分式方程的定义】
【例1】（2022·贵州贵阳·二模）下列关于x的方程，是分式方程的是（ ）
A．x2−3=x5B．12x−13y=5C．xπ=x3+x2D．12+x=1−2x
【变式1-1】（2022·四川省内江市第六中学二模）下列方程中，不是分式方程的是（ ）
A．x+1x=3B．1x=2
C．xx−4=5xx−4D．2x−14−x3=12
【变式1-2】（2022·河南省淮滨县第一中学模拟预测）下列方程：①1x+1=x；②x+12−3=0；③2x−1+31−x=3；④xa+xb=1（a,b为已知数），其中分式方程有（ ）
A．1个B．2个C．3个D．4个
【变式1-3】（2022·全国·九年级专题练习）在下列方程组中，（ ）是分式方程．
A．x2x−1＝1B．2x3=2
C．1x+2=3xD．x+234x5−6=−7
【考点2 分式方程的解】
【例2】（2022·浙江·宁波市鄞州实验中学模拟预测）在正实数范围内，只存在一个数是关于x的方程x2+kx+3x−1=3x+k的解，求实数k的取值范围.
【变式2-1】（2022·黑龙江·中考真题）已知关于x的分式方程m+32x−1=1的解为非负数，则m的取值范围是（ ）
A．m≥−4B．m≥−4且m≠−3C．m>−4D．m>−4且m≠−3
【变式2-2】（2022·黑龙江齐齐哈尔·中考真题）若关于x的分式方程1x−2+2x+2=x+2mx2−4的解大于1，则m的取值范围是______________．
【变式2-3】（2022·四川达州·中考真题）若分式方程2x−ax−1−4=−2x+ax+1的解为整数，则整数a=___________．
【要点2 分式方程的解法】
①将分式方程化成整式方程（去分母，即等号两边同乘以最简公分母）；
②解整式方程（去括号；移项；合并同类项；系数化为1或其它解法）；
③检验：将所得的根代入最简公分母，若等于零，就是增根，应该舍去；若不等于零，就是原方程的根。
【考点3 解分式方程】
【例3】（2022·辽宁营口·中考真题）分式方程3x=2x−2的解是（ ）
A．x=2B．x=−6C．x=6D．x=−2
【变式3-1】（2022·湖南永州·中考真题）解分式方程2x−1x+1=0去分母时，方程两边同乘的最简公分母是______．
【变式3-2】（2022·浙江台州·中考真题）如图的解题过程中，第①步出现错误，但最后所求的值是正确的，则图中被污染的x的值是____．
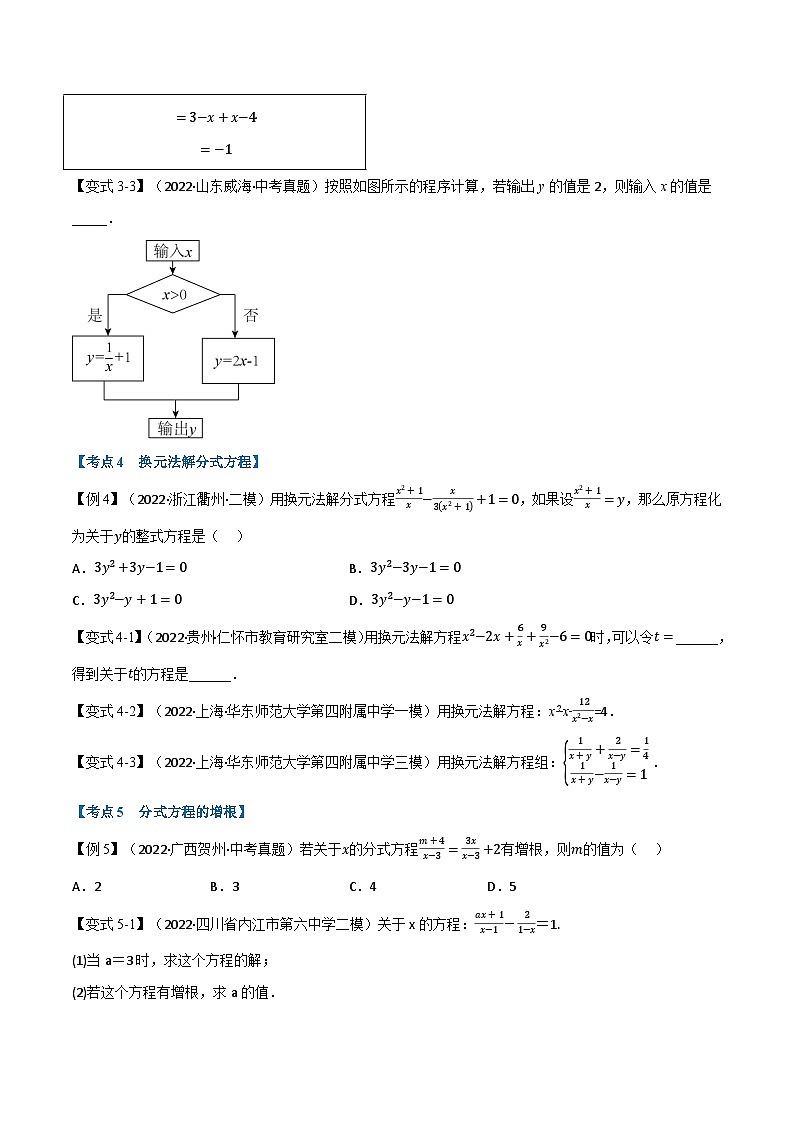
【变式3-3】（2022·山东威海·中考真题）按照如图所示的程序计算，若输出y的值是2，则输入x的值是 _____．
【考点4 换元法解分式方程】
【例4】（2022·浙江衢州·二模）用换元法解分式方程x2+1x−x3x2+1+1=0，如果设x2+1x=y，那么原方程化为关于y的整式方程是（ ）
A．3y2+3y−1=0B．3y2−3y−1=0
C．3y2−y+1=0D．3y2−y−1=0
【变式4-1】（2022·贵州·仁怀市教育研究室二模）用换元法解方程x2−2x+6x+9x2−6=0时，可以令t=______，得到关于t的方程是______．
【变式4-2】（2022·上海·华东师范大学第四附属中学一模）用换元法解方程：x2﹣x﹣12x2−x=4．
【变式4-3】（2022·上海·华东师范大学第四附属中学三模）用换元法解方程组：1x+y+2x−y=141x+y−1x−y=1．
【考点5 分式方程的增根】
【例5】（2022·广西贺州·中考真题）若关于x的分式方程m+4x−3=3xx−3+2有增根，则m的值为（ ）
A．2B．3C．4D．5
【变式5-1】（2022·四川省内江市第六中学二模）关于x的方程：ax+1x−1－21−x＝1.
(1)当a＝3时，求这个方程的解；
(2)若这个方程有增根，求a的值．
【变式5-2】（2022·河北·顺平县腰山镇第一初级中学一模）关于x的分式方程mx−2+12−x=1有增根，则(﹣1)m=（ ）
A．﹣1B．1C．2D．5
【变式5-3】（2022·黑龙江齐齐哈尔·三模）增根是在分式方程转化为整式方程的过程中产生的，分式方程的增根，不是分式方程的根，而是该分式方程化成的整式方程的根，所以涉及分式方程的增根问题的解题步骤通常为：①去分母，化分式方程为整式方程；②将增根代入整式方程中，求出方程中字母系数的值．
阅读以上材料后，完成下列探究：
探究1：m为何值时，方程3xx−3+5=m3−x有增根．
探究2：m为何值时，方程3xx−3+5=m3−x的根是−1．
探究3：任意写出三个m的值，使对应的方程3xx−3+5=m3−x的三个根中两个根之和等于第三个根；
探究4：你发现满足“探究3”条件的m1、m2、m3的关系是______．
【考点6 分式方程的无解】
【例6】（2022·浙江温州·模拟预测）设a，b为实数，关于x的方程xx−1+x−1x=a+bxx2−x无实数根，求代数式8a+4b+|8a+4b-5|的值．
【变式6-1】（2022·四川遂宁·中考真题）若关于x的方程2x=m2x+1无解，则m的值为（ ）
A．0B．4或6C．6D．0或4
【变式6-2】（2022·四川巴中·中考真题）关于x的分式方程m+x2−x−3＝0有解，则实数m应满足的条件是（ ）
A．m＝﹣2B．m≠﹣2C．m＝2D．m≠2
【变式6-3】（2022·安徽·宣州市雁翅乡初级中学二模）对于非零实数a、b，规定a⊗b=ba．若x−3⊗3−2x=0，则x的值为_______________；若关于x的方程x−3⊗3−2x−3−x⊗mx−2=−1无解，则m的值为_______________．
【考点7 不等式与分式方程的综合】
【例7】（2022·重庆·中考真题）关于x的分式方程3x−ax−3+x+13−x=1的解为正数，且关于y的不等式组y+9≤2(y+2)2y−a3>1的解集为y≥5，则所有满足条件的整数a的值之和是（ ）
A．13B．15C．18D．20
【变式7-1】（2022·重庆·中考真题）关于x的分式方程ax−3x−2+1=3x−12−x的解为正数，且使关于y的一元一次不等式组3y−22≤y−1y+2>a有解，则所有满足条件的整数a的值之和是（ ）
A．−5B．−4C．−3D．−2
【变式7-2】（2022·重庆八中模拟预测）从−7，−5，−1，0，1，3这六个数中，随机抽一个数，记为m，若数m使关于x的不等式组x−m2>0x−41，且关于x的分式方程1−x2−x+mx−2=3有非负整数解，则符合条件的m的值的个数是（ ）
A．1个B．2个C．3个D．4个
【变式7-3】（2022·重庆市第三十七中学校二模）若数a既使得关于x的不等式组x−a2+1≤x+a3x−2a>6无解，又使得关于y的分式方程5y−2−a−y2−y=1的解不小于1，则满足条件的所有整数a的和为( )
A．−4B．−3C．−2D．−5
【考点8 分式方程中的新定义问题】
【例8】（2022·湖南怀化·中考真题）定义a⊗b=2a+1b，则方程3⊗x=4⊗2的解为（ ）
A．x=15B．x=25C．x=35D．x=45
【变式8-1】（2022·内蒙古鄂尔多斯·二模）对于实数a、b，定义一种新运算“⊗”为：a⊗b=1a−b2，这里等式右边是实数运算．例如：1⊗3=11−32=−18．则方程x⊗−2=2x−4−1的解是（ ）
A．x=5B．x=6C．x=7D．x=8
【变式8-2】（2022·广东·深圳市宝安中学（集团）模拟预测）对于实数x和y，定义一种新运算“*”：x∗y=1x2+y，这里等式右边是实数运算．例如：1∗2=112+2=13，则方程2∗x=1x−4+1的解是__________．
【变式8-3】（2022·浙江宁波·中考真题）定义一种新运算：对于任意的非零实数a，b，a⊗b=1a+1b．若(x+1)⊗x=2x+1x，则x的值为___________．
【考点9 由实际问题抽象出分式方程】
【例9】（2022·辽宁阜新·中考真题）我市某区为30万人接种新冠疫苗，由于市民积极配合这项工作，实际每天接种人数是原计划的1.2倍，结果提前20天完成了这项工作．设原计划每天接种x万人，根据题意，所列方程正确的是（ ）
A．30x−301.2x=20B．30x−30x−20=1.2
C．301.2x−30x=20D．30x−20−30x=1.2
【变式9-1】（2022·辽宁鞍山·中考真题）某加工厂接到一笔订单，甲、乙车间同时加工，已知乙车间每天加工的产品数量是甲车间每天加工的产品数量的1.5倍，甲车间加工4000件比乙车间加工4200件多用3天．设甲车间每天加工x件产品，根据题意可列方程为_________．
【变式9-2】（2022·山东青岛·中考真题）为落实青岛市中小学生“十个一”行动计划，学校举办以“强体质，炼意志”为主题的体育节，小亮报名参加3000米比赛项目，经过一段时间训练后，比赛时小亮的平均速度比训练前提高了25%，少用3分钟跑完全程．设小亮训练前的平均速度为x米/分，那么x满足的分式方程为__________．
【变式9-3】（2022·山东潍坊·中考真题）观察我国原油进口月度走势图，2022年4月原油进口量比2021年4月增加267万吨，当月增速为6.6%（计算方法：2674036×100%≈6.6%）．2022年3月当月增速为−14.0%，设2021年3月原油进口量为x万吨，下列算法正确的是（ ）
A．x−42714271×100%=−14.0%B．4271−x4271×100%=−14.0%
C．x−4271x×100%=−14.0%D．4271−xx×100%=−14.0%
【考点10 分式方程的应用】
【例10】（2022·浙江衢州·中考真题）金师傅近期准备换车，看中了价格相同的两款国产车．
(1)用含a的代数式表示新能源车的每千米行驶费用．
(2)若燃油车的每千米行驶费用比新能源车多0.54元．
①分别求出这两款车的每千米行驶费用．
②若燃油车和新能源车每年的其它费用分别为4800元和7500元．问：每年行驶里程为多少千米时，买新能源车的年费用更低？（年费用=年行驶费用+年其它费用）
【变式10-2】（2022·重庆·中考真题）在全民健身运动中，骑行运动颇受市民青睐，甲、乙两骑行爱好者约定从A地沿相同路线骑行去距A地30千米的B地，已知甲骑行的速度是乙的1.2倍．
(1)若乙先骑行2千米，甲才开始从A地出发，则甲出发半小时恰好追上乙，求甲骑行的速度；
(2)若乙先骑行20分钟，甲才开始从A地出发，则甲、乙恰好同时到达B地，求甲骑行的速度．
【变式10-3】（2022·湖南益阳·中考真题）在某市组织的农机推广活动中，甲、乙两人分别操控A、B两种型号的收割机参加水稻收割比赛．已知乙每小时收割的亩数比甲少40%，两人各收割6亩水稻，乙则比甲多用0.4小时完成任务；甲、乙在收割过程中对应收稻谷有一定的遗落或破损，损失率分别为3%，2%．
(1)甲、乙两人操控A、B型号收割机每小时各能收割多少亩水稻？
(2)某水稻种植大户有与比赛中规格相同的100亩待收水稻，邀请甲、乙两人操控原收割机一同前去完成收割任务，要求平均损失率不超过2.4%，则最多安排甲收割多少小时？ 先化简，再求值：3−xx−4+1，其中x=
解：原式=3−xx−4⋅(x−4)+(x−4)
=3−x+x−4
=−1
专题06 分式方程及其应用（10个高频考点）（举一反三）

TOC \ "1-1" \h \u
\l "_Tc11773" 【考点1 分式方程的定义】 PAGEREF _Tc11773 \h 1
\l "_Tc31517" 【考点2 分式方程的解】 PAGEREF _Tc31517 \h 3
\l "_Tc4787" 【考点3 解分式方程】 PAGEREF _Tc4787 \h 5
\l "_Tc26689" 【考点4 换元法解分式方程】 PAGEREF _Tc26689 \h 7
\l "_Tc1809" 【考点5 分式方程的增根】 PAGEREF _Tc1809 \h 10
\l "_Tc12008" 【考点6 分式方程的无解】 PAGEREF _Tc12008 \h 12
\l "_Tc17027" 【考点7 不等式与分式方程的综合】 PAGEREF _Tc17027 \h 15
\l "_Tc24191" 【考点8 分式方程中的新定义问题】 PAGEREF _Tc24191 \h 19
\l "_Tc23951" 【考点9 由实际问题抽象出分式方程】 PAGEREF _Tc23951 \h 21
\l "_Tc8456" 【考点10 分式方程的应用】 PAGEREF _Tc8456 \h 23
【要点1 分式方程的定义】
分母中含有未知数的方程叫做分式方程。
【考点1 分式方程的定义】
【例1】（2022·贵州贵阳·二模）下列关于x的方程，是分式方程的是（ ）
A．x2−3=x5B．12x−13y=5C．xπ=x3+x2D．12+x=1−2x
【答案】D
【分析】根据分式方程的定义：分母里含有字母的方程叫做分式方程进行判断．
【详解】解：A．方程分母中不含未知数，故不是分式方程，不符合题意；
B．方程分母中不含未知数，故不是分式方程，不符合题意；
C．方程分母中不含表示未知数的字母，π是常数，故不是分式方程，不符合题意；
D．方程分母中含未知数x，故是分式方程，符合题意．
故选：D．
【点睛】本题主要考查了分式方程的定义，解题的关键是掌握判断一个方程是否为分式方程，主要是依据分式方程的定义，也就是看分母中是否含有未知数（注意：仅仅是字母不行，必须是表示未知数的字母）．
【变式1-1】（2022·四川省内江市第六中学二模）下列方程中，不是分式方程的是（ ）
A．x+1x=3B．1x=2
C．xx−4=5xx−4D．2x−14−x3=12
【答案】D
【分析】根据分式方程的定义逐项判断分母中是否含有未知数即可.
【详解】A、分母中含有未知数，是分式方程，故本选项不符合题意；
B、分母中含有未知数，是分式方程，故本选项不符合题意；
C、分母中含有未知数，是分式方程，故本选项不符合题意；
D、分母中不含未知数，不是分式方程，故本选项符合题意.
故选：D.
【点睛】本题考查分式方程的定义，熟练掌握定义是关键.
【变式1-2】（2022·河南省淮滨县第一中学模拟预测）下列方程：①1x+1=x；②x+12−3=0；③2x−1+31−x=3；④xa+xb=1（a,b为已知数），其中分式方程有（ ）
A．1个B．2个C．3个D．4个
【答案】B
【分析】等号两边至少有一个分母含有未知数的有理方程叫做分式方程；
【详解】解：观察各方程的分母，只有①③分母中含有未知数，而④中分母虽含有字母，但字母不是未知数，故不是分式方程，所以方程①③是分式方程，方程②④均属于整式方程．
故选：B．
【点睛】本题考查分式方程的定义，掌握定义是解题关键．
【变式1-3】（2022·全国·九年级专题练习）在下列方程组中，（ ）是分式方程．
A．x2x−1＝1B．2x3=2
C．1x+2=3xD．x+234x5−6=−7
【答案】A
【分析】根据分式方程定义进行解答即可．
【详解】A、是分式方程，故此选项符合题意；
B、不是分式方程，是整式方程，故此选项不符合题意；
C、不是分式方程，故此选项不符合题意；
D、不是分式方程，是整式方程，故此选项不符合题意；
故选：A．
【点睛】此题主要考查了分式方程，关键是掌握分母中含有未知数的方程叫做分式方程．
【考点2 分式方程的解】
【例2】（2022·浙江·宁波市鄞州实验中学模拟预测）在正实数范围内，只存在一个数是关于x的方程x2+kx+3x−1=3x+k的解，求实数k的取值范围.
【答案】k=−338或k＝-4或k≥-3
【分析】分四种情况讨论：原方程去分母化为2x2−3x−(k+3)=0①．（1）当Δ=0时，−32−4×2×−k+3=8k+33=0，得到k=−338，方程有两个相同的正实根，原方程只存在一个正实数解；（2）原方程的增根x=1是方程2x2−3x−(k+3)=0的一个根，代入得到2×12−3×1−(k+3)=0，得到k=−4代入方程有另一正实数解，原方程只存在一个正实数解；（3）当方程①有异号二实根时，根据根与系数的关系x1x2=−k−32−3，原方程只有一个正实数根；（4）当方程①有一个根为0时，推出k=−3，原方程只有一正实数根．
【详解】解：原方程可化为2x2−3x−(k+3)=0①，
（1）当Δ=−32−4×2×−k+3=8k+33=0时，k=−338，
x1=x2=32×2=34，符合题意；
（2）当x=1是方程①的根时，2×12−3×1−(k+3)=0，k=−4，
此时方程①为，2x2−3x+1=0，解得另一个根为x=12，
故原方程也只有一根x=12；
（3）当方程①有异号实根时，x1x2=−k−32−3，此时原方程也只有一个正实数根；
（4）当方程①有一个根为0时，k=−3，另一个根为x=32，此时原方程也只有一个正实根．
综上所述，满足条件的k的取值范围是：k=−338或k=−4或k≥−3．
【点睛】本题主要考查了分式方程的解与字母系数的关系，解决问题的关键是熟练掌握解分式方程的方法，增根的定义和特点，根据根的情况确定字母系数的取值，一元二次方程根的判别式和根与系数的关系，分类讨论．
【变式2-1】（2022·黑龙江·中考真题）已知关于x的分式方程m+32x−1=1的解为非负数，则m的取值范围是（ ）
A．m≥−4B．m≥−4且m≠−3C．m>−4D．m>−4且m≠−3
【答案】B
【分析】根据题意先求出分式方程的解，然后根据方程的解为非负数可进行求解．
【详解】解：由关于x的分式方程m+32x−1=1可得：x=m+42，且x≠12，
∵方程的解为非负数，
∴m+42≥0，且m+42≠12，
解得：m≥−4且m≠−3，
故选B．
【点睛】本题主要考查分式方程的解法及一元一次不等式的解法，熟练掌握分式方程的解法及一元一次不等式的解法是解题的关键．
【变式2-2】（2022·黑龙江齐齐哈尔·中考真题）若关于x的分式方程1x−2+2x+2=x+2mx2−4的解大于1，则m的取值范围是______________．
【答案】m >0且m≠1
【分析】先解分式方程得到解为x=m+1，根据解大于1得到关于m的不等式再求出m的取值范围，然后再验算分母不为0即可．
【详解】解：方程两边同时乘以x+2x−2得到：x+2+2(x−2)=x+2m，
整理得到：x=m+1，
∵分式方程的解大于1，
∴m+1>1，解得：m>0，
又分式方程的分母不为0，
∴m+1≠2且m+1≠−2，解得：m≠1且m≠−3，
∴m的取值范围是m >0且m≠1．
故答案为：m >0且m≠1．
【点睛】本题考查分式方程的解法，属于基础题，要注意分式方程的分母不为0这个隐藏条件．
【变式2-3】（2022·四川达州·中考真题）若分式方程2x−ax−1−4=−2x+ax+1的解为整数，则整数a=___________．
【答案】±1
【分析】直接移项后通分合并同类项，化简、用a来表示x，再根据解为整数来确定a的值．
【详解】解：2x−ax−1−4=−2x+ax+1，
2x−ax−1−−2x+ax+1=4
(2x−a)(x+1)−(a−2x)(x−1)(x−1)(x+1)=4
整理得：x=2a
若分式方程2x−ax−1−4=−2x+ax+1的解为整数，
∵a为整数，
当a=±1时，解得：x=±2，经检验：x−1≠0,x+1≠0成立；
当a=±2时，解得：x=±1，经检验：分母为0没有意义，故舍去；
综上:a=±1，
故答案是：±1．
【点睛】本题考查了分式方程，解题的关键是：化简分式方程，最终用a来表示x，再根据解为整数来确定a的值，易错点，容易忽略对根的检验．
【要点2 分式方程的解法】
①将分式方程化成整式方程（去分母，即等号两边同乘以最简公分母）；
②解整式方程（去括号；移项；合并同类项；系数化为1或其它解法）；
③检验：将所得的根代入最简公分母，若等于零，就是增根，应该舍去；若不等于零，就是原方程的根。
【考点3 解分式方程】
【例3】（2022·辽宁营口·中考真题）分式方程3x=2x−2的解是（ ）
A．x=2B．x=−6C．x=6D．x=−2
【答案】C
【分析】先去分母，去括号，移项，合并同类项得出答案，最后检验即可．
【详解】解：3x=2x−2，
去分母，得3(x−2)=2x，
去括号，得3x−6=2x，
移项，得3x−2x=6，
所以x=6．
经检验，x=6是原方程的解．
故选：C．
【点睛】本题主要考查了解分式方程，掌握解分式方程的步骤是解题的关键．
【变式3-1】（2022·湖南永州·中考真题）解分式方程2x−1x+1=0去分母时，方程两边同乘的最简公分母是______．
【答案】xx+1
【分析】根据解分式方程的方法中确定公分母的方法求解即可．
【详解】解：分式方程2x−1x+1=0的两个分母分别为x，(x+1)，
∴最简公分母为：x(x+1)，
故答案为：x(x+1)．
【点睛】题目主要考查解分式方程中确定公分母的方法，熟练掌握解分式方程的步骤是解题关键．
【变式3-2】（2022·浙江台州·中考真题）如图的解题过程中，第①步出现错误，但最后所求的值是正确的，则图中被污染的x的值是____．
【答案】5
【分析】根据题意得到方程3−xx−4+1=−1，解方程即可求解．
【详解】解：依题意得：3−xx−4+1=−1，即3−xx−4+2=0，
去分母得：3-x+2(x-4)=0，
去括号得：3-x+2x-8=0，
解得：x=5，
经检验，x=5是方程的解，
故答案为：5．
【点睛】本题考查了解分式方程，一定要注意解分式方程必须检验．
【变式3-3】（2022·山东威海·中考真题）按照如图所示的程序计算，若输出y的值是2，则输入x的值是 _____．
【答案】1
【分析】根据程序分析即可求解．
【详解】解：∵输出y的值是2，
∴上一步计算为2=1x+1或2=2x−1
解得x=1（经检验，x=1是原方程的解），或x=32
当x=1>0符合程序判断条件，x=32>0不符合程序判断条件
故答案为：1
【点睛】本题考查了解分式方程，理解题意是解题的关键．
【考点4 换元法解分式方程】
【例4】（2022·浙江衢州·二模）用换元法解分式方程x2+1x−x3x2+1+1=0，如果设x2+1x=y，那么原方程化为关于y的整式方程是（ ）
A．3y2+3y−1=0B．3y2−3y−1=0
C．3y2−y+1=0D．3y2−y−1=0
【答案】A
【分析】由x2+1x=y，原方程可化为y−13y+1=0，去分母把分式方程化成整式方程，即可得出答案．
【详解】解：设x2+1x=y，
∴分式方程x2+1x−x3x2+1+1=0可化为y−13y+1=0，
化为整式方程：3y2+3y−1=0，
故选：A．
【点睛】本题考查了换元法解分式方程，掌握换元法及正确把分式方程化成整式方程是解决问题的关键．
【变式4-1】（2022·贵州·仁怀市教育研究室二模）用换元法解方程x2−2x+6x+9x2−6=0时，可以令t=______，得到关于t的方程是______．
【答案】 x−3x（答案不唯一） t2−2t=0（答案不唯一）
【分析】利用完全平方公式将x2−2x+6x+9x2−6=0变形为x−3x2−2x−3x=0，令t=x−3x或t=3x−x，进入换元即可．
【详解】解：∵ x2−2x+6x+9x2−6=0，
∴x2−6+9x2−2x−6x=0，
∴x−3x2−2x−3x=0，
令t=x−3x，可得t2−2t=0；
令t=3x−x，可得−t2−2−t=0，即t2+2t=0．
故答案为：x−3x，t2−2t=0或3x−x，t2+2t=0．
【点睛】本题考查换元法解方程，利用完全平方公式将原式变形为x−3x2−2x−3x=0是解题的关键．
【变式4-2】（2022·上海·华东师范大学第四附属中学一模）用换元法解方程：x2﹣x﹣12x2−x=4．
【答案】x1=3，x2=−2
【分析】方程的两个部分是倒数关系，所以可设x2−x=y，可用换元法转化为关于y的分式方程，先求y，再求x，最后检验一下结果．
【详解】设x2−x=y，
则原方程变形为y−12y−4=0，
即y2−4y−12=0，
解得y1=−2，y2=6，
当y=-2时，x2−x+2=0，
因为△=1−8=−91的解集为y≥5，则所有满足条件的整数a的值之和是（ ）
A．13B．15C．18D．20
【答案】A
【分析】先通过分式方程求出a的一个取值范围，再通过不等式组的解集求出a的另一个取值范围，两个范围结合起来就得到a的有限个整数解．
【详解】由分式方程的解为整数可得：3x−a−x−1=x−3
解得：x=a−2
又题意得：a−2>0且a−2≠3
∴a>2且a≠5，
由y+9≤2y+2得：y≥5
由2y−a3>1得：y>3+a2
∵解集为y≥5
∴3+a20且a+4≠3，再由该一元一次不等式组有解，又可以得到a−20，a+4≠3;
∴a>−4，且a≠−1；
∵关于y的元一次不等式组3y−22≤y−1①y+2>a②有解，
由①得：y≤0;
由②得：y>a−2;
∴a−21
∵不等式组的解集为x>1，
∴m≤1，
由1−x2−x+mx−2=3可得：1−x−m=3(2−x)，
解得x=5+m2
由题意可得，x≥0，且x≠2
可得：m≥−5，且m≠−1
此时m的取值为−5，0，1
又∵x为整数，
∴m的取值为−5，1，个数为2
故选：B
【点睛】此题考查了分式方程的解、解一元一次不等式组，熟练掌握运算法则是解本题的关键．
【变式7-3】（2022·重庆市第三十七中学校二模）若数a既使得关于x的不等式组x−a2+1≤x+a3x−2a>6无解，又使得关于y的分式方程5y−2−a−y2−y=1的解不小于1，则满足条件的所有整数a的和为( )
A．−4B．−3C．−2D．−5
【答案】C
【分析】先根据关于x的不等式组无解求出数a的范围，再根据关于y的分式方程的解不小于1求出数a的范围，然后再取数a的范围的公共部分，从而即可求解．
【详解】解：解不等式x−a2+1≤x+a3，得x≤5a−6，
解不等式x−2a>6，得x>2a+6，
∵于x的不等式组x−a2+1≤x+a3x−2a>6无解，
∴5a−6≤2a+6，
∴a≤4；
又解分式方程5y−2−a−y2−y=1，得y=a+72且y≠2，
∵关于y的分式方程5y−2−a−y2−y=1的解不小于1，
∴a+72≥1且a+72≠2，
∴a≥−5且a≠−3；
综上可知：−5≤a5000，
答：每年行驶里程超过5000千米时，买新能源车的年费用更低．
【点睛】本题考查了列代数式、分式方程的应用、一元一次不等式的应用，正确建立方程和不等式是解题关键．
【变式10-1】（2022·山东东营·中考真题）为满足顾客的购物需求，某水果店计划购进甲、乙两种水果进行销售.经了解，甲水果的进价比乙水果的进价低20%，水果店用1000元购进甲种水果比用1200元购进乙种水果的重量多10千克，已知甲，乙两种水果的售价分别为6元/千克和8元/千克.
(1)求甲、乙两种水果的进价分别是多少？
(2)若水果店购进这两种水果共150千克，其中甲种水果的重量不低于乙种水果重量的2倍，则水果店应如何进货才能获得最大利润，最大利润是多少？
【答案】(1)甲种水果的进价是4元/千克，乙种水果的进价是5元/千克；
(2)水果店购进甲种水果100千克，乙种水果50千克时获得最大利润，最大利润是350元．
【分析】（1）设乙种水果的进价是x元/千克，根据“甲水果的进价比乙水果的进价低20%，水果店用1000元购进甲种水果比用1200元购进乙种水果的重量多10千克”列出分式方程，解方程检验后可得出答案；
（2）设水果店购进甲种水果a千克，获得的利润为y元，则购进乙种水果（150－a）千克，根据利润＝（售价－进价）×数量列出y关于a的一次函数解析式，求出a的取值范围，然后利用一次函数的性质解答．
【详解】（1）解：设乙种水果的进价是x元/千克，
由题意得：10001−20%x=1200x+10，
解得：x=5，
经检验，x=5是分式方程的解且符合题意，
则1−20%x=0.8×5=4，
答：甲种水果的进价是4元/千克，乙种水果的进价是5元/千克；
（2）解：设水果店购进甲种水果a千克，获得的利润为y元，则购进乙种水果（150－a）千克，
由题意得：y=6−4a+8−5150−a=−a+450，
∵－1＜0，
∴y随a的增大而减小，
∵甲种水果的重量不低于乙种水果重量的2倍，
∴a≥2150−a，
解得：a≥100，
∴当a=100时，y取最大值，此时y=−100+450=350，150−a=50，
答：水果店购进甲种水果100千克，乙种水果50千克时获得最大利润，最大利润是350元．
【点睛】本题考查了分式方程的应用，一次函数与一元一次不等式的应用，正确理解题意，找出合适的等量关系列出方程和解析式是解题的关键．
【变式10-2】（2022·重庆·中考真题）在全民健身运动中，骑行运动颇受市民青睐，甲、乙两骑行爱好者约定从A地沿相同路线骑行去距A地30千米的B地，已知甲骑行的速度是乙的1.2倍．
(1)若乙先骑行2千米，甲才开始从A地出发，则甲出发半小时恰好追上乙，求甲骑行的速度；
(2)若乙先骑行20分钟，甲才开始从A地出发，则甲、乙恰好同时到达B地，求甲骑行的速度．
【答案】(1)24千米/时
(2)18千米/时
【分析】（1）设乙的速度为x千米/时，则甲的速度为1.2x千米/时，根据甲出发半小时恰好追上乙列方程求解即可；
（2）设乙的速度为x千米/时，则甲的速度为1.2x千米/时，根据甲、乙恰好同时到达B地列方程求解即可．
(1)
解：设乙的速度为x千米/时，则甲的速度为1.2x千米/时，
由题意得：0.5×1.2x=0.5x+2，
解得：x=20，
则1.2x=24，
答：甲骑行的速度为24千米/时；
(2)
设乙的速度为x千米/时，则甲的速度为1.2x千米/时，
由题意得：30x−13=301.2x，
解得x=15，
经检验x=15是分式方程的解，
则1.2x=18，
答：甲骑行的速度为18千米/时．
【点睛】本题考查了一元一次方程的应用和分式方程的应用，找准等量关系，正确列出方程是解题的关键．
【变式10-3】（2022·湖南益阳·中考真题）在某市组织的农机推广活动中，甲、乙两人分别操控A、B两种型号的收割机参加水稻收割比赛．已知乙每小时收割的亩数比甲少40%，两人各收割6亩水稻，乙则比甲多用0.4小时完成任务；甲、乙在收割过程中对应收稻谷有一定的遗落或破损，损失率分别为3%，2%．
(1)甲、乙两人操控A、B型号收割机每小时各能收割多少亩水稻？
(2)某水稻种植大户有与比赛中规格相同的100亩待收水稻，邀请甲、乙两人操控原收割机一同前去完成收割任务，要求平均损失率不超过2.4%，则最多安排甲收割多少小时？
【答案】(1)甲操控A型号收割机每小时收割10亩水稻，乙操控B型号收割机每小时收割6亩水稻
(2)最多安排甲收割4小时
【分析】（1）设甲操控A型号收割机每小时收割x亩水稻，则乙操控B型号收割机每小时收割（1﹣40%）x亩水稻，利用工作时间＝工作总量÷工作效率，结合乙比甲多用0.4小时完成任务，即可得出关于x的分式方程，解之经检验后即可求出甲操控A型号收割机每小时收割水稻的亩数，再将其代入（1﹣40）x中即可求出乙操控B型号收割机每小时收割水稻的亩数；
（2）设安排甲收割y小时，则安排乙收割100−10y6小时，根据要求平均损失率不超过2.4%，即可得出关于y的一元一次不等式，解之取其中的最大值即可得出结论．
（1）解：设甲操控A型号收割机每小时收割x亩水稻，则乙操控B型号收割机每小时收割（1﹣40%）x亩水稻，依题意得：6(1−40%)x−6x=0.4，解得：x＝10，经检验，x＝10是原方程的解，且符合题意，∴（1﹣40%）x＝（1﹣40%）×10＝6．答：甲操控A型号收割机每小时收割10亩水稻，乙操控B型号收割机每小时收割6亩水稻．
（2）设安排甲收割y小时，则安排乙收割100−10y6小时，依题意得：3%×10y＋2%×6×100−10y6≤2.4%×100，解得：y≤4．答：最多安排甲收割4小时．
【点睛】本题考查了分式方程的应用以及一元一次不等式的应用，解题的关键是：（1）找准等量关系，正确列出分式方程；（2）根据各数量之间的关系，正确列出一元一次不等式． 先化简，再求值：3−xx−4+1，其中x=
解：原式=3−xx−4⋅(x−4)+(x−4)
=3−x+x−4
=−1