中考数学总复习举一反三系列(通用版)专题25投影与视图(10个高频考点)(强化训练)(全国通用)(原卷版+解析)

这是一份中考数学总复习举一反三系列(通用版)专题25投影与视图(10个高频考点)(强化训练)(全国通用)(原卷版+解析)，共57页。
1．（2022·湖北襄阳·统考中考真题）襄阳牛杂面因襄阳籍航天员聂海胜的一句“最想吃的还是我们襄阳的牛杂面”火爆出圈，引发了全国人民的聚焦和关注．襄阳某品牌牛杂面的包装盒及对应的立体图形如图所示，则该立体图形的主视图为（ ）
A．B．C．D．
2．（2022·广东深圳·统考中考真题）下列图形中，主视图和左视图一样的是（ ）
A．B．C．D．
3．（2022·贵州黔西·统考中考真题）如图，是由6个相同的正方体组成的立体图形，它的俯视图是（ ）
A．B．C．D．
4．（2022·浙江金华·统考中考真题）从一个边长为3cm的大立方体挖去一个边长为1cm的小立方体，得到的几何体如图所示，则该几何体的左视图正确的是（ ）
A．B．C．D．
5．（2022·浙江杭州·中考真题）小明从正面观察下图所示的两个物体，看到的是（ ）
A．AB．BC．CD．D
【题型2 根据三视图确定几何体】
6．（2022·云南·中考真题）下列图形是某几何体的三视图（其中主视图也称正视图，左视图也称侧视图），则这个几何体是（ ）
A．三棱柱B．三棱锥C．四棱柱D．圆柱
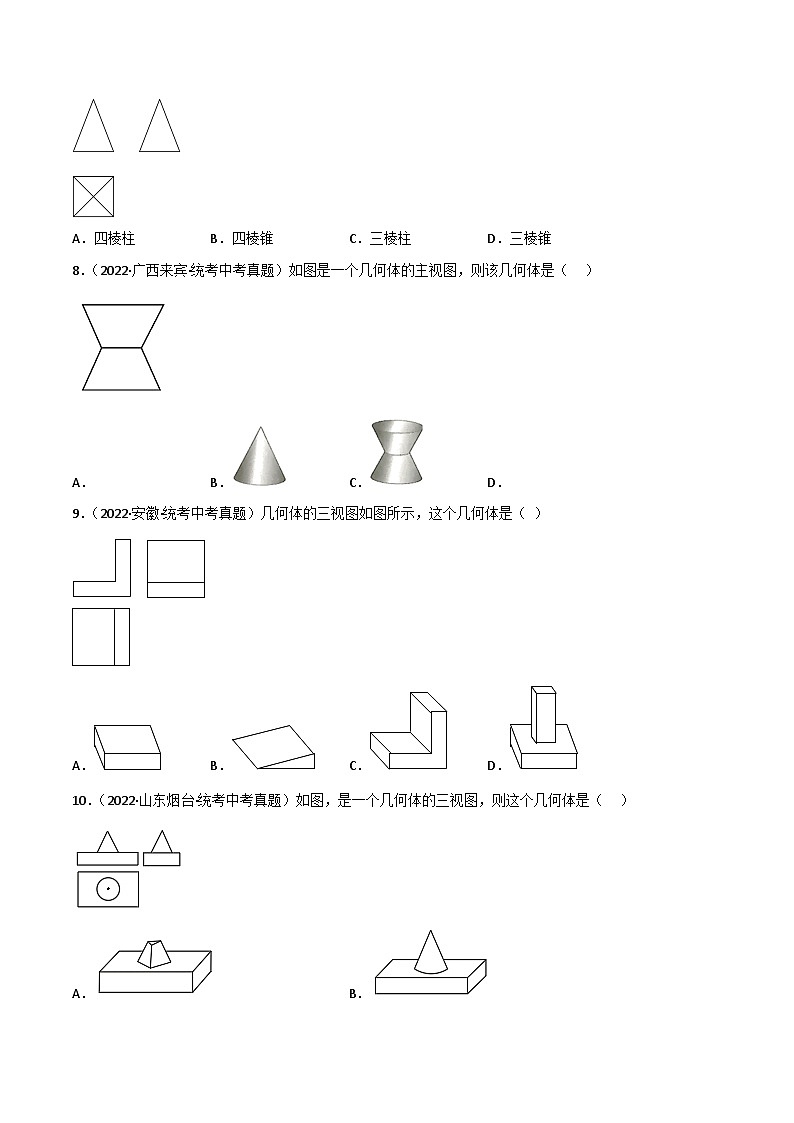
7．（2022·江苏扬州·统考中考真题）如图是某一几何体的主视图、左视图、俯视图，该几何体是（ ）
A．四棱柱B．四棱锥C．三棱柱D．三棱锥
8．（2022·广西来宾·统考中考真题）如图是一个几何体的主视图，则该几何体是（ ）
A．B．C．D．
9．（2022·安徽·统考中考真题）几何体的三视图如图所示，这个几何体是（ ）
A．B．C．D．
10．（2022·山东烟台·统考中考真题）如图，是一个几何体的三视图，则这个几何体是（ ）
A．B．
C．D．
【题型3 在格点中作几何体的三视图】
11．（2011·上海·统考中考模拟）作图与推理：如图，是由一些大小相同的小正方体组合成的简单几何体
（1）图中有 块小正方体；
（2）从正面看到该几何体的形状图如图所示，请在下面方格纸中分别画出从左面，上面看到该几何体的形状图
12．（2022·江苏盐城·校联考三模）如图是由一些棱长都为1cm的小正方体组合成的简单几何体．
（1）该几何体的主视图如图所示，请在下面方格纸中分别画出它的左视图和俯视图；
（2）如果在这个几何体上再添加一些小正方体，并保持俯视图和左视图不变，最多可以再添加 块小正方体．
13．（2022·山东淄博·中考真题）由一些相同的小正方体搭成的几何体的左视图和俯视图如图所示，请在网格中涂出一种该几何体的主视图，且使该主视图是轴对称图形．
14．（2022·湖北咸宁·统考一模）如图1，是由一些棱长为单位1的相同的小正方体组合成的简单几何体．
（1）图中有 个小正方体；
（2）请在图1右侧方格中分别画出几何体的主视图、左视图；
（3）不改变（2）中所画的主视图和左视图，最多还能在图1中添加 个小正方体．
15．（2022·河北邯郸·校考一模）如图（1）是一种包装盒的表面展开图，将它围起来可得到一个几何体的模型．
(1)图（2）是根据a，h的取值画出的几何体的主视图和俯视图，请在网格中画出该几何体的左视图；
(2)已知h＝4，求a的值和该几何体的表面积．
【题型4 根据三视图确定小立方体的个数】
16．（2022·广东深圳·校考一模）（1）如图1，若将一个小立方块①移走，则变化后的几何体与变化前的几何体从______看到的形状图没有发生改变；（填“正面”、“上面”或“左面”）
（2）如图2，请画出由6个小立方块搭成的几何体从上面看到的形状图；
（3）一个几何体由大小相同的小立方块搭成，从上面看到的几何体的形状图如图3所示，小正方形中的数字表示该位置上的小立方块的个数，请画出从左面看到的形状图．
17．（2022·甘肃定西·校联考一模）一个几何体是由若干个棱长为3cm的小正方体搭成的，从正面、左面、上面看到的几何体的形状图如图所示：
（1）在“从上面看”的图中标出各个位置上小正方体的个数；
（2）求该几何体的体积．
18．（2022·甘肃天水·校考模拟预测）如图是由几个相同的边长为1个单位的小立方块搭成的几何体从上面看到的形状，方格中的数字表示该位置的小立方块的个数．
（1）请在方格纸中分别画出从正面和左面所观察到的几何体的形状；
（2）由三个不同方向所观察到的图形可知这个组合几何体的表面积为________个平方单位（包括底面积）．
19．（2022秋·广东佛山·模拟预测）一个几何体由大小相同的小立方块搭成，从上面看到的几何体的形状如图所示，其中小正方形中的数字表示在该位置的小立方块的个数，请画出从正面和从左面看到的这个几何体的形状图．
20．（2022秋·宁夏银川·七年级校考阶段练习）如图所示，这是一个由小立方体所搭成的几何体从上面看到的形状图，小正方形中的数字表示该位置的小立方体的个数．
(1)请在方格纸中用阴影画出从它的正面和左面看到的形状图；
(2)求这个几何体的表面积．
【题型5 根据三视图确定最多或最少的小立方体的个数】
21．（2022·山东威海·校联考一模）如图是由一些大小相同的小正方体组成的几何体．
（1）画出从正面、左面、上面看到的这个几何体的形状图．
（2）若还有一些相同的小正方体，如果保持从上面看和从左面看到的图形不变，最多可以再添加 个小正方体．
22．（2022·山东青岛·二模）如图是由一些棱长均为1个单位长度的小正方体组合成的简单几何体．
(1)画该几何体的主视图、左视图：
(2)若给该几何体露在外面的面（不含底图）都喷上红漆，则需要喷漆的面积是 ；
(3)如果在这个几何体上再添加一些小正方体，并保持主视图和左视图不变，则最多可以再添加 块小正方体．
23．（2022秋·河北保定·模拟预测）用若干大小相同的小正方体搭一个几何体，使得从正面和从上面看到的这个几何体的形状如图所示，完成下列问题：
(1)搭成满足如图所示的几何体最多需要______个小正方体，最少需要______个小正方体；
(2)请在网格中画出用最多小正方体搭成的几何体从左面看到的形状图．
24．（2022秋·宁夏银川·七年级校考阶段练习）用小立方体搭一个几何体，使它从左面看和从上面看的形状图如图所示，从上面看的形状图中的小正方形中字母表示该位置小立方块的个数，试回答下列问题：
(1)b，d，e各等于几？
(2)这个几何体最少由几个小立方块搭成？最多呢？（写出计算过程）
(3)当a=1，c=f=3时，在方格纸中用阴影画出这个几何体从正面看到的形状图．
25．（2022春·河北模拟预测）根据要求完成下列题目：
(1)请在下面方格纸中分别画出它的主视图，左视图和俯视图．
(2)用小立方体搭一几何体，使得它的俯视图和左视图与你在上图方格中所画的图一致，则这样的几何体最少要 个小立方块，最多要 个小立方块．
27．（2022·山东威海·校联考一模）如图是由几个同样大小的小正方体所搭几何体从上面看到的形状图，小正方形中的数字表示该位置的小正方体的个数．请画出这个几何体从正面、左面看到的形状图．
28．（2022春·广东茂名·模拟预测）如图，是一个小正方体所搭几何体从上面看得到的平面图形，正方形中的数字表示在该位置小正方体的个数，请你画出它从正面和从左面看得到的平面图形．
29．（2022秋·河南平顶山·模拟预测）一个几何体由几个大小相同的小立方块搭成，从上面观察这个几何体，看到的形状如图所示，其中小正方形中的数字表示在该位置的小立方块的个数，请画出从正面、左面看到的这个几何体的形状图．
30．（2022秋·山东烟台·模拟预测）一个几何体由大小相同的小正方体搭成，从上面看到的几何体的形状如图所示，其中小正方形中的数字表示在该位置的小正方体个数．
(1)请画出从正面和从左面看到的这个几何体的形状图．
(2)若小正方体的棱长为2，求该几何体的体积和表面积．
【题型7 去掉或移动小立方体确定视图是否改变】
31．（2022·江苏扬州·统考二模）如图是由6个大小相同的小正方体拼成的几何体，当去掉某一个小正方体时，与原几何体比较，则下列说法正确的是 （ ）
A．去掉①，主视图不变B．去掉②，俯视图不变
C．去掉③，左视图不变D．去掉④, 俯视图不变
32．（2022·广东深圳·校考模拟预测）如图是由6个相同的小正方体搭成的几何体，若去掉上层的一个小正方体，则下列说法正确的是（ ）．
A．主视图一定变化B．左视图一定变化
C．俯视图一定变化D．三种视图都不变化
33．（2022·辽宁朝阳·统考一模）如图是由6个大小相同的小正方体拼成的几何体，若去掉最上面的小正方体，则下列说法正确的是（ ）
A．主视图不变B．左视图不变C．俯视图不变D．三种视图都不变
34．（2022秋·河北石家庄·九年级石家庄二十三中模拟预测）如图是由几个大小相同的小正方体搭成的几何体，若去掉1号小正方体，则下列说法正确的是（ ）
A．左视图和俯视图不变B．主视图和左视图不变
C．主视图和俯视图不变D．都不变
35．（2022·江苏扬州·统考二模）如图是由6个大小相同的小正方体拼成的几何体，若去掉最左面的小正方体，则视图不发生改变的是________（填主视图、左视图或俯视图）
【题型8 平行投影的概念及特点】
36．（2022·四川成都·统考一模）如图，AB和DE是直立在地面上的两根立柱，AB=5m，某一时刻AB在阳光下的投影BC=3m，同时测量出DE在阳光下的投影长为6m，则DE的长为______．
37．（2022·辽宁铁岭·统考三模）如图，日晷是我国古代利用日影测定时刻的仪器，晷针在晷面上所形成的投影属于______投影．
38．（2022·江苏泰州·校考一模）小刚身高1.7m，测得他站立在阳光下的影子长为0.85m，紧接着他把手臂竖直举起，测得影子长为1.11m，那么小刚举起的手臂超出头顶________．
39．（2022·浙江温州·统考中考真题）如图是某风车示意图，其相同的四个叶片均匀分布，水平地面上的点M在旋转中心O的正下方．某一时刻，太阳光线恰好垂直照射叶片OA,OB，此时各叶片影子在点M右侧成线段CD，测得MC=8.5m,CD=13m，垂直于地面的木棒EF与影子FG的比为2∶3，则点O，M之间的距离等于___________米．转动时，叶片外端离地面的最大高度等于___________米．
40．（2022·广西百色·中考真题）如图，长方体的一个底面ABCD在投影面P上，M，N分别是侧棱BF，CG的中点，矩形EFGH与矩形EMNH的投影都是矩形ABCD，设它们的面积分别是S1，S2，S，则S1，S2，S的关系是_____（用“=、＞或＜”连起来）
【题型9 中心投影的概念及特点】
41．（2010·江苏扬州·中考真题）如图，楼房和旗杆在路灯下的影子如图所示．
（1）试确定路灯灯泡的位置；
（2）再作出小树在路灯下的影子．（用线段表示，不写作法，保留作图痕迹）
42．（2022·江苏镇江·统考中考真题）某兴趣小组开展课外活动．如图，A，B两地相距12米，小明从点A出发沿AB方向匀速前进，2秒后到达点D，此时他（CD）在某一灯光下的影长为AD，继续按原速行走2秒到达点F，此时他在同一灯光下的影子仍落在其身后，并测得这个影长为1.2米，然后他将速度提高到原来的1.5倍，再行走2秒到达点H，此时他（GH）在同一灯光下的影长为BH（点C，E，G在一条直线上）．
（1）请在图中画出光源O点的位置，并画出他位于点F时在这个灯光下的影长FM（不写画法）；
（2）求小明原来的速度．
43．（2022·安徽滁州·校考一模）学习投影后，小明、小颖利用灯光下自己的影子长度来测量一路灯的高度，并探究影子长度的变化规律．如图，在同一时间，身高为1.6m的小明(AB)的影子BC长是3m，而小颖(EH)刚好在路灯灯泡的正下方H点，并测得HB=6m．
(1)请在图中画出形成影子的光线，并确定路灯灯泡所在的位置G；
(2)求路灯灯泡的垂直高度GH；
(3)如果小明沿线段BH向小颖（点H)走去，当小明走到BH中点B1处时，求其影子B1C1的长；当小明继续走剩下路程的13到B2处时，求其影子B2C2的长；当小明继续走剩下路程的14到B3处，…按此规律继续走下去，当小明走剩下路程的1n+1到Bn处时，其影子BnCn的长为 m．（直接用n的代数式表示）
44．（2022·安徽宿州·统考一模）我国古代数学家赵爽利用影子对物体进行测量的方法，至今仍有借鉴意义．如图1，身高1.5m的小王晚上在路灯灯柱AH下散步，他想通过测量自己的影长来估计路灯的高度，具体做法如下：先从路灯底部A向东走20步到M处，发现自己的影子端点落在点P处，作好记号后，继续沿刚才自己的影子走4步恰好到达点P处，此时影子的端点在点Q处，已知小王和灯柱的底端在同一水平线上，小王的步间距保持一致．
(1)请在图中画出路灯O和影子端点Q的位置．
(2)估计路灯AO的高，并求影长PQ的步数．
(3)无论点光源还是视线，其本质是相同的，日常生活中我们也可以直接利用视线解决问题．如图2，小明同学用自制的直角三角形纸板DEF测量树的高度AB，他调整自己的位置，设法使斜边DF保持水平，并且边DE与点B在同一直线上．测得DF=0.5m，EF=0.3m，CD=10m，小明眼睛到地面的距离为1.5m，则树高AB为______m．
45．（2022·四川自贡·校考一模）为方便住校生晚自习后回到宿舍就寝，新安装了一批照明路灯；一天上午小刚在观看新安的照明灯时，发现在太阳光的正面照射下，照明灯的灯杆的投影的末端恰好落在2.5米高文化走廊墙的顶端，小刚测得照明灯的灯杆的在太阳光下的投影从灯杆的杆脚到文化走廊的墙脚的影长为4.6米，同一时刻另外一个前来观看照明路灯小静测得身高1.5米小刚站立时在太阳光下的影长恰好为1米，请同学们画出与问题相关联的线条示意图并求出新安装的照明路灯的灯杆的高度？
【题型10 正投影的概念及特点】
46．（2022·江西·模拟预测）如图1所示的是一户外遮阳伞支架张开的状态，图1可抽象成图2，在图2中，点A可在BD上滑动，当伞完全折叠成图3时，伞的下端点F落在F′处，点C落在C′处，AE=EF，AC=BC=CE=90cm，DF′=70cm．
(1)BD的长为______．
(2)如图2，当AB=54cm时．
①求∠ACB的度数；（参考数据：sin17.5°≈0.30，tan16.7°≈0.30，sin36.9°≈0.60，tan31.0°≈0.60）
②求伞能遮雨的面积（伞的正投影可以看作一个圆）．
47．（2022·江苏扬州·校联考二模）如图 1，在平面直角坐标系中，图形 W在坐标轴上的投影长度定义如下：设点 P(x1 , y1 ) ，Q(x2 , y2) 是图形 W 上的任意两点，若x1−x2的最大值为 m ，则
图形 W 在 x 轴上的投影长度为 lx  m ；若y1−y2的最大值为 n ，则图形 W 在 y 轴上的
投影长度为 ly  n ．如图 1，图形 W 在 x 轴上的投影长度为 lx 4−0  4 ；在 y 轴上的 投影长度为 ly 3−0 3 ．
（1）已知点 A(1, 2) ， B(2, 3) ， C (3,1) ，如图 2 所示，若图形 W 为四边形 OABC ，
则 lx  ， ly  ；
（2）已知点 C (32, 0) ，点 D 在直线 y  12x  1(x  0) 上，若图形 W 为 OCD ，当 lx  ly
时，求点 D 的坐标；
（3 ）若图形 W 为函数 y  x 2(a  x  b) 的图象，其中 (0  a  b) ，当该图形满足
lx  ly  1时，请直接写出 a 的取值范围．
图 1 图 2
48．（2022·江苏扬州·统考中考真题）如图，平面内的两条直线l1、l2,点A、B在直线l2上，过点A、B两点分别作直线l1的垂线，垂足分别为A1、B1，我们把线段A1B1叫做线段AB在直线l2上的正投影，其长度可记作T（AB，CD）或T（AB，l2）,特别地，线段AC在直线l2上的正投影就是线段A1C，请依据上述定义解决如下问题.
（1）如图1，在锐角△ABC中，AB=5，T（AC，AB）=3，则T（BC，AB）= ；
（2）如图2，在Rt△ABC中，∠ACB=90°，T（AC，AB）=4，T（BC，AB）=9，求△ABC的面积；
（3）如图3，在钝角△ABC中，∠A=60°，点D在AB边上，∠ACD=90°，T（AD，AC）=2，T（BC，AB）=6，求T（BC，CD）.
49．（2022·福建厦门·统考三模）如图是某校校史荣誉室的正方形网格平面图，实线表示墙体或门．在点A处安装了360度旋转摄像头，由于墙体的的遮挡，阴影部分无法监控，这部分无法监控到的区域通常称为监控盲区．
（1）小红同学进入校史荣誉室随意参观，站在监控盲区的概率是多少？
（2）为了监控效果更好，使得监控盲区最小，请你帮助学校在墙体AB上重新设计摄像头安装的位置，画出示意图，并说明理由．
50．（2022·福建漳州·统考一模）如图，现有m、n两堵墙，两个同学分别在A处和B处，请问小明在哪个区域内活动才不会被这两个同学发现（画图用阴影表示）．

专题25 投影与视图（10个高频考点）（强化训练）
【题型1 判断几何体的三视图】
1．（2022·湖北襄阳·统考中考真题）襄阳牛杂面因襄阳籍航天员聂海胜的一句“最想吃的还是我们襄阳的牛杂面”火爆出圈，引发了全国人民的聚焦和关注．襄阳某品牌牛杂面的包装盒及对应的立体图形如图所示，则该立体图形的主视图为（ ）
A．B．C．D．
【答案】A
【分析】根据主视图的意义，从正面看该立体图形所得到的图形进行判断即可．
【详解】解：从正面看，是一个矩形，
故选：A．
【点睛】本题考查简单几何体的主视图，理解三视图的意义，掌握三视图的画法是正确判断的关键．
2．（2022·广东深圳·统考中考真题）下列图形中，主视图和左视图一样的是（ ）
A．B．C．D．
【答案】D
【分析】根据各个几何体的主视图和左视图进行判定即可．
【详解】解：A．主视图和左视图不相同，故本选项不合题意；
B．主视图和左视图不相同，故本选项不合题意；
C．主视图和左视图不相同，故本选项不合题意；
D．主视图和左视图相同，故本选项符合题意；
故选：D．
【点睛】本题考查简单几何体的三视图，解题的关键是掌握各种几何体的三视图的形状．
3．（2022·贵州黔西·统考中考真题）如图，是由6个相同的正方体组成的立体图形，它的俯视图是（ ）
A．B．C．D．
【答案】C
【分析】找到从上面看，能看到的图形即可，即俯视图．
【详解】该立体图形的俯视图为：
故：C．
【点睛】本题考查了三视图的知识，正确确定三视图是本题的关键．
4．（2022·浙江金华·统考中考真题）从一个边长为3cm的大立方体挖去一个边长为1cm的小立方体，得到的几何体如图所示，则该几何体的左视图正确的是（ ）
A．B．C．D．
【答案】C
【详解】左视图就是从物体的左边往右边看．小正方形应该在右上角，故B错误，看不到的线要用虚线，故A错误，大立方体的边长为3cm，挖去的小立方体边长为1cm，所以小正方形的边长应该是大正方形13，故D错误，所以C正确．
故此题选C．
5．（2022·浙江杭州·中考真题）小明从正面观察下图所示的两个物体，看到的是（ ）
A．AB．BC．CD．D
【答案】C
【分析】主视图是从正面看到的图形
【详解】主视图是从正面看到的图形，圆柱从正面看是长方形，正方体从正面看是正方形，所以从左往右摆放一个圆柱体和一个正方体，它们的主视图是左边一个长方形，右边一个正方形．
故选：C．
【点睛】本题考查了主视图，理解主视图是从正面看到的图形是解题关键.
【题型2 根据三视图确定几何体】
6．（2022·云南·中考真题）下列图形是某几何体的三视图（其中主视图也称正视图，左视图也称侧视图），则这个几何体是（ ）
A．三棱柱B．三棱锥C．四棱柱D．圆柱
【答案】D
【分析】根据三视图逆向即可得．
【详解】解：此几何体为一个圆柱．
故选：D．
【点睛】此题考查由三视图还原几何体，既要考虑各视图的形状，还要把各视图的情况综合考虑才能得到几何体的形状．
7．（2022·江苏扬州·统考中考真题）如图是某一几何体的主视图、左视图、俯视图，该几何体是（ ）
A．四棱柱B．四棱锥C．三棱柱D．三棱锥
【答案】B
【分析】根据各个几何体三视图的特点进行求解即可．
【详解】解：∵该几何体的主视图与左视图都是三角形，俯视图是一个矩形，而且两条对角线是实线，
∴该几何体是四棱锥，
故选B．
【点睛】本题主要考查了由三视图还原几何体，熟知常见几何体的三视图是解题的关键．
8．（2022·广西来宾·统考中考真题）如图是一个几何体的主视图，则该几何体是（ ）
A．B．C．D．
【答案】C
【分析】主视图、左视图、俯视图是分别从物体正面、左面和上面看，所得到的图形．依题意，由几何体的主视图即可判断该几何体的形状．
【详解】解：由该几何体的主视图可知，该几何体是选项C中的图形．
故选：C．
【点睛】本题考查了由三视图判断几何体，考查学生对三视图掌握程度和灵活运用能力，同时也考查了空间想象能力．
9．（2022·安徽·统考中考真题）几何体的三视图如图所示，这个几何体是（ ）
A．B．C．D．
【答案】C
【分析】根据三视图，该几何体的主视图可确定该几何体的形状，据此求解即可．
【详解】解：根据A，B，C，D三个选项的物体的主视图可知，与题图有吻合的只有C选项，
故选：C．
【点睛】本题考查了由三视图判断几何体的知识，熟练掌握三视图并能灵活运用，是解题的关键．
10．（2022·山东烟台·统考中考真题）如图，是一个几何体的三视图，则这个几何体是（ ）
A．B．
C．D．
【答案】B
【分析】结合三视图确定各图形的位置后即可确定正确的选项．
【详解】解：结合三个视图发现，这个几何体是长方体和圆锥的组合图形．
故选：B．
【点睛】本题考查了由三视图判断几何体的知识，解题的关键是能够正确的确定各个图形的位置，难度不大．
【题型3 在格点中作几何体的三视图】
11．（2011·上海·统考中考模拟）作图与推理：如图，是由一些大小相同的小正方体组合成的简单几何体
（1）图中有 块小正方体；
（2）从正面看到该几何体的形状图如图所示，请在下面方格纸中分别画出从左面，上面看到该几何体的形状图
【答案】（1）11; （2）图形见解析.
【分析】（1）根据如图所示即可得出图中小正方体的个数；
（2）读图可得，左视图有2列，每列小正方形数目分别为2，2；俯视图有4列，每行小正方形数目分别为2，2，1，1．
【详解】解：（1）2×5+1＝11（块）．
即图中有11块小正方体，
故答案为11；
（2）如图所示；左视图，俯视图分别如下图：
【点睛】此题主要考查实物体的三视图．在画图时一定要将物体的边缘、棱、顶点都体现出来，看得见的轮廓线都画成实线，看不见的画成虚线，不能漏掉．本题画几何体的三视图时应注意小正方形的数目及位置．
12．（2022·江苏盐城·校联考三模）如图是由一些棱长都为1cm的小正方体组合成的简单几何体．
（1）该几何体的主视图如图所示，请在下面方格纸中分别画出它的左视图和俯视图；
（2）如果在这个几何体上再添加一些小正方体，并保持俯视图和左视图不变，最多可以再添加 块小正方体．
【答案】（1）作图见解析；（2）6
【分析】(1)根据长对正，高平齐和宽相等的法则画出三视图；
(2)根据三视图的法则得出立体图形，从而得出答案．
【详解】解：（1）如图所示：
（2）保持俯视图和左视图不变，最多可以再添加6块小正方体.
故答案为6．
【点睛】此题主要考查了作三视图，在画图时一定要将物体的边缘、棱、顶点都体现出来，看得见的轮廓线都画成实线，看不见的画成虚线，不能漏掉．
13．（2022·山东淄博·中考真题）由一些相同的小正方体搭成的几何体的左视图和俯视图如图所示，请在网格中涂出一种该几何体的主视图，且使该主视图是轴对称图形．
【答案】作图见解析
【分析】根据俯视图和左视图可知，该几何体共两层，底层有9个正方体，上层中间一行有正方体，若使主视图为轴对称图形可使中间一行、中间一列有一个小正方体即可．
【详解】解：由三视图与轴对称图形，作图即可，
【点睛】本题考查了几何体的三视图，轴对称图形．解题的关键在于熟练掌握三视图．
14．（2022·湖北咸宁·统考一模）如图1，是由一些棱长为单位1的相同的小正方体组合成的简单几何体．
（1）图中有 个小正方体；
（2）请在图1右侧方格中分别画出几何体的主视图、左视图；
（3）不改变（2）中所画的主视图和左视图，最多还能在图1中添加 个小正方体．
【答案】（1）10；（2）见解析；（3）4.
【分析】（1）最前面1排1个小正方体，中间1排有3个正方体，最后面一排共6个小正方体，再计算总和即可；
（2）由已知条件可知，主视图有3列，每列小正方数形数目分别为3，1，2，左视图有3列，每列小正方形数目分别为3，2，1，据此可画出图形；
（3）不改变（2）中所画的主视图和左视图，最多还能在图1中添加第一排的右边2列的2个，第2排的右边第3列的2个，然后可得答案．
【详解】解：（1）依图可知，图中有1+3+6=10个小正方体；
（2）该几何体的主视图、左视图如下：
（3）不改变（2）中所画的主视图和左视图，最多还能在图1中添加第一排的右边2列的2个，第2排的右边第3列的2个，所以可添加4个小正方体.
【点睛】本题考查三视图.主要考查空间思维能力.（1）中需注意不要忽略了底层看不见的正方体；（2）中需注意画正方体的堆积体的三视图时应注意小正方形的数目及位置；（3）可在不影响主视图的前提下尝试添加正方体，然后依照左视图判断.
15．（2022·河北邯郸·校考一模）如图（1）是一种包装盒的表面展开图，将它围起来可得到一个几何体的模型．
(1)图（2）是根据a，h的取值画出的几何体的主视图和俯视图，请在网格中画出该几何体的左视图；
(2)已知h＝4，求a的值和该几何体的表面积．
【答案】(1)见解析
(2)a的值为22，该几何体的表面积为162＋24．
【分析】（1）根据三视图的画法即可画出该几何体的左视图；
（2）根据俯视图和主视图即可求a的值，进而可求该几何体的表面积．
【详解】（1）解：如图所示，图中的左视图即为所求；
（2）解：根据俯视图和主视图可知：
a2＋a2＝h2＝42，
解得a＝22，
几何体的表面积为：2ah＋2ah＋12a2×2＝162＋24．
答：a的值为22，该几何体的表面积为162＋24．
【点睛】本题考查了作图−三视图、几何体的表面积、展开图折叠成几何体，解决本题的关键是理解立体图形和平面图形之间的关系．
【题型4 根据三视图确定小立方体的个数】
16．（2022·广东深圳·校考一模）（1）如图1，若将一个小立方块①移走，则变化后的几何体与变化前的几何体从______看到的形状图没有发生改变；（填“正面”、“上面”或“左面”）
（2）如图2，请画出由6个小立方块搭成的几何体从上面看到的形状图；
（3）一个几何体由大小相同的小立方块搭成，从上面看到的几何体的形状图如图3所示，小正方形中的数字表示该位置上的小立方块的个数，请画出从左面看到的形状图．
【答案】（1）正面
（2）见解析
（2）见解析
【分析】（1）根据三视图的定义判断即可；
（2）根据三视图的定义，画出图形即可；
（3）根据三视图的定义，画出图形即可．
【详解】解：（1）如图1，将一个正方体①移走后，变化后的几何体与变化前的几何体从正面看到的形状图相同．
故答案为：正面；
（2）如图所示：
（3）如图所示：
【点睛】本题考查作图﹣三视图，解题的关键是理解三视图的定义，属于中考常考题型．
17．（2022·甘肃定西·校联考一模）一个几何体是由若干个棱长为3cm的小正方体搭成的，从正面、左面、上面看到的几何体的形状图如图所示：
（1）在“从上面看”的图中标出各个位置上小正方体的个数；
（2）求该几何体的体积．
【答案】（1）见解析；（2）270cm3
【分析】（1）根据“俯视图打地基，主视图疯狂盖，左视图拆违章”的原则解答即可得；
（2）根据每个正方体的体积乘以正方体的个数即可得．
【详解】（1）如图所示：
（2）该几何体的体积为33×（2+3+2+1+1+1）=27×10=270（cm3）．
【点睛】本题考查了学生对三视图的掌握程度和灵活运用能力，同时也体现了对空间想象能力方面的考查．如果掌握口诀“俯视图打地基，主视图疯狂盖，左视图拆违章”就更容易得到答案．
18．（2022·甘肃天水·校考模拟预测）如图是由几个相同的边长为1个单位的小立方块搭成的几何体从上面看到的形状，方格中的数字表示该位置的小立方块的个数．
（1）请在方格纸中分别画出从正面和左面所观察到的几何体的形状；
（2）由三个不同方向所观察到的图形可知这个组合几何体的表面积为________个平方单位（包括底面积）．
【答案】（1）图见解析；（2）24
【分析】（1）从正面看有2列，每列小正方形数目分别为2，3；从左面看有2列，每列小正方形数目分别为3，1；
（2）上面共有3个小正方形，下面共有3个小正方形；左面共有4个小正方形，右面共有4个正方形；前面共有5个小正方形，后面共有5个正方形，继而可得出表面积．
【详解】解：（1）如图所示
（2）根据从三个方向看的形状图，这个几何体的表面积为2×（5+4+3）＝24（平方单位），
故答案为：24．
【点睛】此题考查了从不同方向看几何体及几何体的表面积的计算，解答本题的关键是掌握立体图形的观察方法．
19．（2022秋·广东佛山·模拟预测）一个几何体由大小相同的小立方块搭成，从上面看到的几何体的形状如图所示，其中小正方形中的数字表示在该位置的小立方块的个数，请画出从正面和从左面看到的这个几何体的形状图．
【答案】见解析
【分析】主视图有3列，每行小正方形数目分别为4，2，3；左视图有3列，每列小正方形数目分别为2，4，3；依此作图即可求解．
【详解】解：如图所示：
【点睛】本题考查作图-三视图．本题画几何体的三视图时应注意小正方形的数目及位置．
20．（2022秋·宁夏银川·七年级校考阶段练习）如图所示，这是一个由小立方体所搭成的几何体从上面看到的形状图，小正方形中的数字表示该位置的小立方体的个数．
(1)请在方格纸中用阴影画出从它的正面和左面看到的形状图；
(2)求这个几何体的表面积．
【答案】(1)见解析
(2)44
【分析】（1）根据从上面看的图形可知，从正面看有3列，从左往右个数分别为3，2，3，从左面看有2列，从左往右分别为3，3，据此可画出图形；
（2）根据几何体的表面积公式即可求解．
【详解】（1）解：作图如下：
（2）该几何体的表面积为：8×2+6×2+5×2+3×2×1=44．
【点睛】本题考查几何体的三视图画法．由几何体的俯视图及小正方形内的数字，可知主视图的列数与俯视图的列数相同，且每列小正方形数目为俯视图中该列小正方形数字中的最大数字．左视图的列数与俯视图的行数相同，且每列小正方形数目为俯视图中相应行中正方形数字中的最大数字，掌握不同方向上看到的图形的画法是解题的关键．
【题型5 根据三视图确定最多或最少的小立方体的个数】
21．（2022·山东威海·校联考一模）如图是由一些大小相同的小正方体组成的几何体．
（1）画出从正面、左面、上面看到的这个几何体的形状图．
（2）若还有一些相同的小正方体，如果保持从上面看和从左面看到的图形不变，最多可以再添加 个小正方体．
【答案】（1）图形见解析（2）4
【详解】分析：根据三视图的定义结合图形可得．
详解：（1）如图所示：
（2）如果保持从上面看和从左面看到的图形不变，最多可以再添加4个小正方体，
故答案为4．
点睛：本题考查作图-三视图．在画图时一定要将物体的边缘、棱、顶点都体现出来，看得见的轮廓线都画成实线，看不见的画成虚线，不能漏掉．本题画几何体的三视图时应注意小正方形的数目及位置．
22．（2022·山东青岛·二模）如图是由一些棱长均为1个单位长度的小正方体组合成的简单几何体．
(1)画该几何体的主视图、左视图：
(2)若给该几何体露在外面的面（不含底图）都喷上红漆，则需要喷漆的面积是 ；
(3)如果在这个几何体上再添加一些小正方体，并保持主视图和左视图不变，则最多可以再添加 块小正方体．
【答案】(1)见详解；
(2)27；
(3)3．
【分析】（1）根据三视图的概念求解可得；
（2）将主视图、左视图分别乘2的面积，加上俯视图的面积即可得解；
（3）若使该几何体主视图和左视图不变，只可在底层添加方块，可以添加3块小正方体．
【详解】（1）如图所示：
（2）解：（7×2＋4×2）×（1×1）＋5×（1×1）
＝14＋8＋5
＝27
故答案为：27．
（3）若使该几何体主视图和左视图不变，可在最底层从右数第一至三列的第一行各添加一个，添加3块小正方体．
故答案为：3．
【点睛】本题主要考查了画三视图，解题的关键是掌握在画图时一定要将物体的边缘、棱、顶点都体现出来，看得见的轮廓线都化成实线，看不见的画成虚线，不能漏掉．本题画几何体的三视图时应注意小正方体的数目及位置．
23．（2022秋·河北保定·模拟预测）用若干大小相同的小正方体搭一个几何体，使得从正面和从上面看到的这个几何体的形状如图所示，完成下列问题：
(1)搭成满足如图所示的几何体最多需要______个小正方体，最少需要______个小正方体；
(2)请在网格中画出用最多小正方体搭成的几何体从左面看到的形状图．
【答案】(1)10，7
(2)见解析
【分析】（1）从上面看，结合从正面看的特征，可得结论；
（2）根据从上面和正面看的图形，解决问题即可．
【详解】（1）解：搭成满足如图所示主视图和俯视图的几何体最多需要：2+2+2+2+2=10（个），
最少需要1+2+1+1+2=7（个）；
故答案为：10，7；
（2）如图所示．
【点睛】本题考查由三视图判断几何体，解题的关键是理解三视图的定义，属于中考常考题型．
24．（2022秋·宁夏银川·七年级校考阶段练习）用小立方体搭一个几何体，使它从左面看和从上面看的形状图如图所示，从上面看的形状图中的小正方形中字母表示该位置小立方块的个数，试回答下列问题：
(1)b，d，e各等于几？
(2)这个几何体最少由几个小立方块搭成？最多呢？（写出计算过程）
(3)当a=1，c=f=3时，在方格纸中用阴影画出这个几何体从正面看到的形状图．
【答案】(1)b=1，d=1，e=2；
(2)最少由9个小立方块搭成，最多由13个小立方块搭成；
(3)见解析
【分析】（1）根据从左面看到的形状可知，第二列小立方体的个数均为1，第3列小正方体的个数为2，那么b=d=1，e=2；
（2）第一列小立方体的个数最多为3+3+3，最少为3+1+1，那么加上其他两列小立方体的个数即可；
（3）从正面看到的形状图有3列，每列小正方形数目分别为1，3，3．
【详解】（1）解：根据从左面看到的形状可知，第二列小立方体的个数均为1，第3列小正方体的个数为2，
∴b=d=1，e=2；
（2）解：由图可知，第一列小立方体的个数最多为3+3+3，最少为3+1+1，
∴这个几何体最多由3+3+3+1+1+2=13个小立方块搭成，最少由3+1+1+1+1+2=9个小立方块搭成；
（3）解：从正面看到的形状图如图所示：
【点睛】本题考查了三视图的知识，主视图是从物体的正面看到的视图，左视图是从物体的左面看到的视图，俯视图是从从物体的上面看到的视图．
25．（2022春·河北模拟预测）根据要求完成下列题目：
(1)请在下面方格纸中分别画出它的主视图，左视图和俯视图．
(2)用小立方体搭一几何体，使得它的俯视图和左视图与你在上图方格中所画的图一致，则这样的几何体最少要 个小立方块，最多要 个小立方块．
【答案】(1)图见详解
(2)5 ， 7
【分析】（1）主视图从左往右小正方形的个数为3，2；左视图从左往右小正方形的个数为3，1；俯视图从左往右小正方形的个数为2，1；
（2）由俯视图易得最底层小立方块的个数，由左视图找到其余层数里最少个数和最多个数相加即可．
【详解】（1）解：根据题意画出图如下：
（2）解：用小立方体搭一几何体，使得它的俯视图和左视图与你在上图方格中所画的图一致，
则这样的几何体最少要5个小立方块，最多要7个小立方块．
故答案为：5，7．
【点睛】本题主要考查了三视图，用到的知识点为：三视图分为主视图、左视图、俯视图，分别是从物体正面、左面和上面看，所得到的图形；俯视图决定底层立方块的个数，易错点是由主视图得到其余层数里最少的立方块个数和最多的立方块个数．
【题型6 根据俯视图中的小正方形中的数字确定其他视图】
26．（2022·福建南平·统考一模）如图是由几个小立方块所搭几何体从上面看到的图形，小正方形中的数字表示在该位置小立方块的个数，请画出相应几何体从正面、从左面看到的图形．
【答案】见解析
【分析】由已知条件可知，从正面看有3列，每列小正方数形数目分别为3，2，2；从左面看有2列，每列小正方形数目分别为3，2．据此可画出图形．
【详解】解：如图所示：
．
【点睛】本题考查了三视图，解题关键是明确从不同方向看到的小正方体个数及位置．
27．（2022·山东威海·校联考一模）如图是由几个同样大小的小正方体所搭几何体从上面看到的形状图，小正方形中的数字表示该位置的小正方体的个数．请画出这个几何体从正面、左面看到的形状图．
【答案】图形见解析
【详解】分析：根据俯视图可得出立方体的组成，进而得出其主视图与左视图．
详解：如图所示，
点睛：此题主要考查了画三视图，正确分析得出图形的组成是解题关键．
28．（2022春·广东茂名·模拟预测）如图，是一个小正方体所搭几何体从上面看得到的平面图形，正方形中的数字表示在该位置小正方体的个数，请你画出它从正面和从左面看得到的平面图形．
【答案】见解析
【分析】根据俯视图上各个位置所摆放的小正方体的个数，画出主视图、左视图即可解答．
【详解】解：画图如下：
．
【点睛】本题主要考查了几何体的三视图画法．由几何体的俯视图及小正方形内的数字，可知主视图的列数与俯视数的列数相同且每列小正方形数目为俯视图中该列小正方形数字中的最大数字．左视图的列数与俯视图的行数相同且每列小正方形数目为俯视图中相应行中正方形数字中的最大数字．
29．（2022秋·河南平顶山·模拟预测）一个几何体由几个大小相同的小立方块搭成，从上面观察这个几何体，看到的形状如图所示，其中小正方形中的数字表示在该位置的小立方块的个数，请画出从正面、左面看到的这个几何体的形状图．
【答案】图形见解析
【分析】由已知条件可知，从正面看有3列，每列小正方形数目分别为3、2、2，从左面看有2列，每列小正方形数目分别为3、2．据此即可画出图形．
【详解】解：如图所示：
【点睛】本题考查几何体的三视图画法．由几何体的俯视图及小正方形内的数字，可知主视图的列数与俯视数的列数相同，且每列小正方形数目为俯视图中该列小正方形数字中的最大数字．左视图的列数与俯视图的行数相同，且每列小正方形数目为俯视图中相应行中正方形数字中的最大数字．
30．（2022秋·山东烟台·模拟预测）一个几何体由大小相同的小正方体搭成，从上面看到的几何体的形状如图所示，其中小正方形中的数字表示在该位置的小正方体个数．
(1)请画出从正面和从左面看到的这个几何体的形状图．
(2)若小正方体的棱长为2，求该几何体的体积和表面积．
【答案】(1)见解析
(2)该几何体的体积为96，几何体的表面积为176
【分析】（1）根据从正面看，从左面看的定义，仔细画出即可；
（2）体积等于立方体的个数×单个的体积；表面积等于上下面的个数即从上面看的图形正方形个数的2倍；左右看的正方形面数，前后看的正方形面数，其和乘以一个正方形的面积即可．
【详解】（1）如图所示，
（2）∵小正方体的棱长为2，
∴每个小正方体的体积为2×2×2=8，
∴该几何体的体积为1+2+1+3+1+4×8=96；
∵，
∴每个小正方形的面积为2×2=4，
∴几何体的上下面的个数为6×2=12个，前后面的个数为9×2=18个，左右面的个数为7×2=14个，
∴几何体的表面积为：12+18+14×4=176．
【点睛】本题考查了从不同方向看，几何体体积和表面积，正确理解确定小正方体的个数是解题的关键．
【题型7 去掉或移动小立方体确定视图是否改变】
31．（2022·江苏扬州·统考二模）如图是由6个大小相同的小正方体拼成的几何体，当去掉某一个小正方体时，与原几何体比较，则下列说法正确的是 （ ）
A．去掉①，主视图不变B．去掉②，俯视图不变
C．去掉③，左视图不变D．去掉④, 俯视图不变
【答案】D
【分析】根据从正面看得到的图形是主视图，从左边看得到的图形是左视图，从上边看得到的图形是俯视图，可得答案．
【详解】解：A.去掉①，左视图不变，主视图改变了，故此选项错误；
B. 去掉②，左视图不变，俯视图改变了，故此选项错误；
C. 去掉③，主视图不变，左视图改变了，故此选项错误；
D. 去掉④, 俯视图不变，说法正确，
故选：D．
【点睛】本题考查了简单组合体的三视图，从正面看得到的图形是主视图，从左边看得到的图形是左视图，从上边看得到的图形是俯视图．
32．（2022·广东深圳·校考模拟预测）如图是由6个相同的小正方体搭成的几何体，若去掉上层的一个小正方体，则下列说法正确的是（ ）．
A．主视图一定变化B．左视图一定变化
C．俯视图一定变化D．三种视图都不变化
【答案】A
【分析】根据从正面看得到的图形是主视图，从左边看得到的图形是左视图，从上边看得到的图形是俯视图，可得答案．
【详解】解:去掉最上面的小正方体，其左视图与俯视图不变，即左视图两层下层两个小正方形，上层一个小正方形,俯视图依然还是两层，底层中间有一个正方形，上层有1个正方形；
变化的是正视图上层有两个，拿走一个，由两个小正方形组成长方形变为一个小正方形．
故答案为：A．
【点睛】本题考查了简单组合体的三视图，从正面看得到的图形是主视图，从左边看得到的图形是左视图，从上边看得到的图形是俯视图，掌握简单组合体的三视图是解题关键．
33．（2022·辽宁朝阳·统考一模）如图是由6个大小相同的小正方体拼成的几何体，若去掉最上面的小正方体，则下列说法正确的是（ ）
A．主视图不变B．左视图不变C．俯视图不变D．三种视图都不变
【答案】C
【分析】根据从正面看得到的图形是主视图，从左边看得到的图形是左视图，从上边看得到的图形是俯视图，可得答案．
【详解】若去掉最上面的小正方体，其俯视图不变，即俯视图依然还是两层，底层中间有一个正方形，上层有3个正方形；
故答案为：C．
【点睛】本题考查了简单组合体的三视图，从正面看得到的图形是主视图，从左边看得到的图形是左视图，从上边看得到的图形是俯视图．
34．（2022秋·河北石家庄·九年级石家庄二十三中模拟预测）如图是由几个大小相同的小正方体搭成的几何体，若去掉1号小正方体，则下列说法正确的是（ ）
A．左视图和俯视图不变B．主视图和左视图不变
C．主视图和俯视图不变D．都不变
【答案】A
【分析】根据从正面看得到的图形是主视图，从左边看得到的图形是左视图，从上边看得到的图形是俯视图，再从看到的小正方形的个数与排列方式两个方面逐一分析可得答案．
【详解】解：若去掉1号小正方体， 主视图一定变化，主视图中最右边的一列由两个小正方形变为一个，
从上面看过去，看到的小正方形的个数与排列方式不变，所以俯视图不变，
从左边看过去，看到的小正方形的个数与排列方式不变； 所以左视图不变，
所以A符合题意，B，C，D不符合题意；
故选：A．
【点睛】本题考查的是由小正方体堆砌而成的图形的三视图，掌握“三视图的含义”是解本题的关键.
35．（2022·江苏扬州·统考二模）如图是由6个大小相同的小正方体拼成的几何体，若去掉最左面的小正方体，则视图不发生改变的是________（填主视图、左视图或俯视图）
【答案】左视图
【分析】画出原立体图形的三视图，与去掉小正方体的立体图形与三视图，对比即可得出答案．
【详解】解：未去掉小正方形的立体图形的三视图为：
去掉最左面的小正方体后立体图形变为：
其三视图
发现其主视图与俯视图都发生改变，
只有左视图不发生改变．
故答案为：左视图．
【点睛】本题考查简单组合体的三视图，减少一个小正方体的组合体的三视图的变化，掌握简单组合体的三视图是解题关键．
【题型8 平行投影的概念及特点】
36．（2022·四川成都·统考一模）如图，AB和DE是直立在地面上的两根立柱，AB=5m，某一时刻AB在阳光下的投影BC=3m，同时测量出DE在阳光下的投影长为6m，则DE的长为______．
【答案】10
【分析】利用同一时刻物体高度与影长比值相等进而得出答案．
【详解】解：如图所示，
∵AB=5m，某一时刻AB在阳光下的投影BC=3m，EF=6m，
∴ABBC=DEEF，则53=DE6，
解得：DE=10，
答：DE的长为10m．
故答案为：10．
【点睛】此题主要考查了相似三角形的应用以及平行投影的性质，得出DE的影子位置是解题关键．
37．（2022·辽宁铁岭·统考三模）如图，日晷是我国古代利用日影测定时刻的仪器，晷针在晷面上所形成的投影属于______投影．
【答案】平行
【分析】根据太阳光是平行光线可以判定晷针在晷面上所形成的投影属于平行投影．
【详解】解：因为太阳光属于平行光线，而日晷利用日影测定时刻，所以晷针在晷面上所形成的投影属于平行投影．
故答案为：平行．
【点睛】本题考查的是平行投影的概念：如果把中心投影法的投射中心移至无穷远处，则各投射线成为相互平行的直线，这种投影法称为平行投影法．
38．（2022·江苏泰州·校考一模）小刚身高1.7m，测得他站立在阳光下的影子长为0.85m，紧接着他把手臂竖直举起，测得影子长为1.11m，那么小刚举起的手臂超出头顶________．
【答案】0.52m
【分析】由题意，得AC//DE，根据平行线分线段成比例求解即可．
【详解】解：如图，由题意，得AC//DE
AB=1.7，BC=0.85，BD=1.11
∴CD= BD- BC=1.11-0.85=0.26
∵AC//DE
∴ABAE=BCCD
∴1.7AE=
∴AE=0.52
故答案为：0.52m．
【点睛】本题考查了平行投影知识，利用平行线分线段成比例求解即可，找出题中的隐含关系是解题的关键．
39．（2022·浙江温州·统考中考真题）如图是某风车示意图，其相同的四个叶片均匀分布，水平地面上的点M在旋转中心O的正下方．某一时刻，太阳光线恰好垂直照射叶片OA,OB，此时各叶片影子在点M右侧成线段CD，测得MC=8.5m,CD=13m，垂直于地面的木棒EF与影子FG的比为2∶3，则点O，M之间的距离等于___________米．转动时，叶片外端离地面的最大高度等于___________米．
【答案】 10 10+13
【分析】过点O作AC、BD的平行线，交CD于H，过点O作水平线OJ交BD于点J，过点B作BI⊥OJ，垂足为I，延长MO，使得OK＝OB，求出CH的长度，根据EFFG=OMMH=23，求出OM的长度，证明△BIO∽△JIB，得出BI=23IJ，OI=49IJ，求出IJ、BI、OI的长度，用勾股定理求出OB的长，即可算出所求长度．
【详解】如图，过点O作AC、BD的平行线，交CD于H，过点O作水平线OJ交BD于点J，过点B作BI⊥OJ，垂足为I，延长MO，使得OK＝OB，
由题意可知，点O是AB的中点，
∵OH∥AC∥BD，
∴点H是CD的中点，
∵CD=13m，
∴CH=HD=12CD=6.5m，
∴MH=MC+CH=8.5+6.5=15m，
又∵由题意可知：EFFG=OMMH=23，
∴OM15=23，解得OM=10m，
∴点O、M之间的距离等于10m，
∵BI⊥OJ，
∴∠BIO=∠BIJ=90°，
∵由题意可知：∠OBJ=∠OBI+∠JBI=90°，
又∵∠BOI+∠OBI=90°，
∴∠BOI=∠JBI，
∴△BIO∽△JIB，
∴BIIJ=OIBI=23，
∴BI=23IJ，OI=49IJ，
∵OJ∥CD,OH∥DJ，
∴四边形IHDJ是平行四边形，
∴OJ=HD=6.5m，
∵OJ=OI+IJ=49IJ+IJ=6.5m，
∴IJ=4.5m，BI=3m，OI=2m，
∵在Rt△OBI中，由勾股定理得：OB2=OI2+BI2，
∴OB=OI2+BI2=22+32=13m，
∴OB=OK=13m，
∴MK=MO+OK=10+13m，
∴叶片外端离地面的最大高度等于10+13m，
故答案为：10，10+13．
【点睛】本题主要考查了投影和相似的应用，及勾股定理和平行四边形的判定与性质，正确作出辅助线是解答本题的关键．
40．（2022·广西百色·中考真题）如图，长方体的一个底面ABCD在投影面P上，M，N分别是侧棱BF，CG的中点，矩形EFGH与矩形EMNH的投影都是矩形ABCD，设它们的面积分别是S1，S2，S，则S1，S2，S的关系是_____（用“=、＞或＜”连起来）
【答案】S1=S＜S2
【分析】根据长方体的概念得到S1=S，根据矩形的面积公式得到S＜S2，得到答案．
【详解】解：∵立体图形是长方体，
∴底面ABCD∥底面EFGH．
∵矩形EFGH的投影是矩形ABCD，
∴S1=S．
∵EM＞EF，EH=EH，
S＜S2，
∴S1=S＜S2．
故答案为S1=S＜S2．
【点睛】本题考查了平行投影和立体图形，平行投影：由平行光线形成的投影是平行投影．
【题型9 中心投影的概念及特点】
41．（2010·江苏扬州·中考真题）如图，楼房和旗杆在路灯下的影子如图所示．
（1）试确定路灯灯泡的位置；
（2）再作出小树在路灯下的影子．（用线段表示，不写作法，保留作图痕迹）
【答案】（1）画图见解析，（2）画图见解析
【分析】（1）根据楼和旗杆的物高与影子得到光源所在；
（2）根据光源和树的物高得影子长．
【详解】解：（1）如图所示，
（2）如图所示．
【点睛】本题考查中心投影的特点与应用，解决本题的关键是得到点光源的位置．
42．（2022·江苏镇江·统考中考真题）某兴趣小组开展课外活动．如图，A，B两地相距12米，小明从点A出发沿AB方向匀速前进，2秒后到达点D，此时他（CD）在某一灯光下的影长为AD，继续按原速行走2秒到达点F，此时他在同一灯光下的影子仍落在其身后，并测得这个影长为1.2米，然后他将速度提高到原来的1.5倍，再行走2秒到达点H，此时他（GH）在同一灯光下的影长为BH（点C，E，G在一条直线上）．
（1）请在图中画出光源O点的位置，并画出他位于点F时在这个灯光下的影长FM（不写画法）；
（2）求小明原来的速度．
【答案】（1）作图见试题解析；（2）1.5m/s．
【分析】（1）利用中心投影的定义作图；
（2）设小明原来的速度为xm/s，则CE=2xm，AM=（4x﹣1.2）m，EG=3xm，BM=13.2﹣4x，由△OCE∽△OAM，△OEG∽△OMB，得到CEAM=EGBM，即代入解方程即可．
【详解】解：（1）如图，
（2）设小明原来的速度为xm/s，
则CE=2xm，AM=AF﹣MF=（4x﹣1.2）m，EG=2×1.5x=3xm，BM=AB﹣AM=12﹣（4x﹣1.2）=13.2﹣4x，
∵点C，E，G在一条直线上，CG∥AB，
∴△OCE∽△OAM，△OEG∽△OMB，
∴CEAM=OEOM，EGBM=OEOM，
∴CEAM=EGBM，即2x4x−1.2=3x13.2−4x，
解得x=1.5，经检验x=1.5为方程的解，
∴小明原来的速度为1.5m/s．
答：小明原来的速度为1.5m/s．
【点睛】本题考查相似三角形的应用以及中心投影，掌握中心投影的定义以及相似三角形的判定与性质是解题关键．
43．（2022·安徽滁州·校考一模）学习投影后，小明、小颖利用灯光下自己的影子长度来测量一路灯的高度，并探究影子长度的变化规律．如图，在同一时间，身高为1.6m的小明(AB)的影子BC长是3m，而小颖(EH)刚好在路灯灯泡的正下方H点，并测得HB=6m．
(1)请在图中画出形成影子的光线，并确定路灯灯泡所在的位置G；
(2)求路灯灯泡的垂直高度GH；
(3)如果小明沿线段BH向小颖（点H)走去，当小明走到BH中点B1处时，求其影子B1C1的长；当小明继续走剩下路程的13到B2处时，求其影子B2C2的长；当小明继续走剩下路程的14到B3处，…按此规律继续走下去，当小明走剩下路程的1n+1到Bn处时，其影子BnCn的长为 m．（直接用n的代数式表示）
【答案】(1)见解析；
(2)4.8m；
(3)3n+1．
【分析】（1）确定灯泡的位置，可以利用光线可逆可以画出；
（2）要求垂直高度GH可以把这个问题转化成相似三角形的问题，图中△ABC∽△GHC，由它们对应成比例可以求出GH；
（3）的方法和（2）一样也是利用三角形相似，对应相等成比例可以求出，然后找出规律．
【详解】（1）解：如图
（2）∵AB⊥HC，GH⊥HC，
∴AB∥GH，
∴△ABC∽△GHC，
∴ ABGH=BCHC，
∵AB=1.6m，BC=3m，HB=6m
∴ 1.6GH=36+3，
∴GH=4.8m．
（3）同理△A1B1C1∽△GHC1，
∴ A1B1GH=B1C1HC1，
设B1C1长为x，则+3，
解得：x=32，即B1C1=32．
同理+2，
解得B2C2=1，
∴+1n+1×6，
可得BnCn=3n+1，
故答案为：3n+1．
【点睛】本题主要考查相似三角形的应用及中心投影，只要是把实际问题抽象到相似三角形中，利用相似三角形的性质对应边成比例解题．
44．（2022·安徽宿州·统考一模）我国古代数学家赵爽利用影子对物体进行测量的方法，至今仍有借鉴意义．如图1，身高1.5m的小王晚上在路灯灯柱AH下散步，他想通过测量自己的影长来估计路灯的高度，具体做法如下：先从路灯底部A向东走20步到M处，发现自己的影子端点落在点P处，作好记号后，继续沿刚才自己的影子走4步恰好到达点P处，此时影子的端点在点Q处，已知小王和灯柱的底端在同一水平线上，小王的步间距保持一致．
(1)请在图中画出路灯O和影子端点Q的位置．
(2)估计路灯AO的高，并求影长PQ的步数．
(3)无论点光源还是视线，其本质是相同的，日常生活中我们也可以直接利用视线解决问题．如图2，小明同学用自制的直角三角形纸板DEF测量树的高度AB，他调整自己的位置，设法使斜边DF保持水平，并且边DE与点B在同一直线上．测得DF=0.5m，EF=0.3m，CD=10m，小明眼睛到地面的距离为1.5m，则树高AB为______m．
【答案】(1)见解析
(2)路灯AO的高为9m，影长PQ为245步
(3)9
【分析】(1)根据中心投影的知识画出图即可．
(2)利用相似三角形的判定和性质计算即可．
(3)利用勾股定理，锐角三角函数，矩形的判定和性质计算即可．
【详解】（1）路灯O和影子端点Q的位置如图所示．
．
（2）∵MN∥OA，
∴△PMN∽△PAO，
∴MNOA=PMPA，即1.5OA=44+20，
解得OA=9．
∵PB∥OA，
∴△QPB∽△QAO，
∴PBOA=PQQA，即1.59=PQPQ+24，
解得PQ=245，
∴路灯AO的高为9m，影长PQ为245步．
（3）如图，∵DF=0.5m，EF=0.3m，∠DEF=90°，
∴DE=DF2−EF2=0.52−0.32=0.4m，
∴tanD=EFDE=，
∵tanD=BCCD=34=BC10，CD=10m，
∴BC=7.5m，
∵四边形ACDG是矩形，
∴DG=AC=1.5m，
∴AB=AC+BC=7.5m+1.5m=9m，
故答案为：9．
【点睛】本题考查了解直角三角形的应用，勾股定理，正切函数，三角形相似的判定和性质，矩形的判定和性质，熟练掌握解直角三角形的应用是解题的关键．
45．（2022·四川自贡·校考一模）为方便住校生晚自习后回到宿舍就寝，新安装了一批照明路灯；一天上午小刚在观看新安的照明灯时，发现在太阳光的正面照射下，照明灯的灯杆的投影的末端恰好落在2.5米高文化走廊墙的顶端，小刚测得照明灯的灯杆的在太阳光下的投影从灯杆的杆脚到文化走廊的墙脚的影长为4.6米，同一时刻另外一个前来观看照明路灯小静测得身高1.5米小刚站立时在太阳光下的影长恰好为1米，请同学们画出与问题相关联的线条示意图并求出新安装的照明路灯的灯杆的高度？
【答案】线条示意图见解析，新安装的照明路灯的灯杆的高度为9.4m.
【分析】利用同一时刻投影的性质得出ABBE=1.51=AB4.6,进而得出答案．
【详解】解:如图所示:过点E作EB⊥AC于点B,
由题意可得:DC=BE=4．6m，DE=BC=2. 5m,
∵同一时刻身高1．5米小刚站立时在太阳光下的影长恰好为1米,
ABBE=1.51=AB4.6
解得: AB=6.9,
∴AC=AB+BC=6.9+2.5=9.4 (m),
答:新安装的照明路灯的灯杆的高度为9.4m．
【点睛】此题主要考查了投影的应用，利用同一时刻影子与高度的关系得出比例式是解题关键．
【题型10 正投影的概念及特点】
46．（2022·江西·模拟预测）如图1所示的是一户外遮阳伞支架张开的状态，图1可抽象成图2，在图2中，点A可在BD上滑动，当伞完全折叠成图3时，伞的下端点F落在F′处，点C落在C′处，AE=EF，AC=BC=CE=90cm，DF′=70cm．
(1)BD的长为______．
(2)如图2，当AB=54cm时．
①求∠ACB的度数；（参考数据：sin17.5°≈0.30，tan16.7°≈0.30，sin36.9°≈0.60，tan31.0°≈0.60）
②求伞能遮雨的面积（伞的正投影可以看作一个圆）．
【答案】(1)250cm
(2)①35°；②29484π
【分析】（1）根据题意可得BD=BF′+F′D，当伞完全折叠成图3时，伞的下端点F落在F′处，点C落在C′处，可得BF′=EF=AC+CE，代入数据求解即可；
（2）①过点C作CG⊥AG，根据BC=AC，可得AG=GB=27cm，∠ACG=12∠ACB，根据sin∠ACG=0.3，sin17.5°≈0.30，即可求解；
②根据题意可知CG∥AF，则∠EAH=17.5°，根据EH=sin17.5°⋅AE求得EH，根据勾股定理可得AH2=AE2−EH2，根据正投影是一个圆，根据圆的面积公式求解即可．
【详解】（1）解：∵BD=BF′+F′D当伞完全折叠成图3时，伞的下端点F落在F′处，点C落在C′处，可得BF′=EF=AC+CE
∴BD=BF′+F′D =EF+F′D=AC+CE+F′D=90+90+70=250cm
（2）①如图，过点C作CG⊥AG
∵BC=AC=90cm，AB=54cm
∴AG=GB=27cm，∠ACG=12∠ACB
sin∠ACG=AGAC=2790=310≈0.3
∴∠ACG=17.5°
∴∠ACB=2∠ACG=35°
②如图，连接AF，过点E作EH⊥AF，
∵AE=EF
∴AH=HF
根据题意可知CG∥AF
∴∠EAH=17.5°
∵AE=180cm
∴EH=sin17.5°⋅AE=0.3×180=54
∴AH2=AE2−EH2=1802−542=29484
∴伞能遮雨的面积为29484π
【点睛】本题考查了解直角三角形的应用，正投影，理解题意是解题的关键．
47．（2022·江苏扬州·校联考二模）如图 1，在平面直角坐标系中，图形 W在坐标轴上的投影长度定义如下：设点 P(x1 , y1 ) ，Q(x2 , y2) 是图形 W 上的任意两点，若x1−x2的最大值为 m ，则
图形 W 在 x 轴上的投影长度为 lx  m ；若y1−y2的最大值为 n ，则图形 W 在 y 轴上的
投影长度为 ly  n ．如图 1，图形 W 在 x 轴上的投影长度为 lx 4−0  4 ；在 y 轴上的 投影长度为 ly 3−0 3 ．
（1）已知点 A(1, 2) ， B(2, 3) ， C (3,1) ，如图 2 所示，若图形 W 为四边形 OABC ，
则 lx  ， ly  ；
（2）已知点 C (32, 0) ，点 D 在直线 y  12x  1(x  0) 上，若图形 W 为 OCD ，当 lx  ly
时，求点 D 的坐标；
（3 ）若图形 W 为函数 y  x 2(a  x  b) 的图象，其中 (0  a  b) ，当该图形满足
lx  ly  1时，请直接写出 a 的取值范围．
图 1 图 2
【答案】（1）4,3;(2)（-23，143）或（-10，-14）;(3) 0≤a