

上海市普陀区2024-2025学年九年级上学期数学期中考试试卷
展开
这是一份上海市普陀区2024-2025学年九年级上学期数学期中考试试卷,共11页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
一、选择题(本大题共6题,每题4分,满分24分)
【下列各题的四个选项中,有且只有一个是正确的,选择正确项的代号并填涂在答题纸的相应位置上】
1.下列函数中,一定为二次函数的是( )
A.B.C.D.
2.已知点P是线段AB的黄金分割点,且,那么下列结论正确的是( )
A.B.
C.D.
3.如图,在中,点D、E和F分别在边AB、AC和BC上,,,如果,那么下列结论中正确的是( )
A.B.C.D.
4.下列关于向量的说法中,正确的是( )
A.如果,那么
B.如果,,那么
C.已知是单位向量,如果,那么
D.如果,,其中是非零向量,那么
5.在同一平面直角坐标系中,画出直线与抛物线,这个图形可能是( )
A.B.
C.D.
6.已知在中,点D、E分别在边AB和AC上,联结CD、BE交于点F,下列条件中,不一定能得到和相似的是( )
A.B.C.D.
二、填空题(本大题共12题,每题4分,满分48分)
【请将结果直接填入答题纸的相应位置】
7.已知,且,那么_______.
8.抛物线与y轴的交点坐标为_______.
9.已知二次函数的图像经过点、,那么该二次函数图像的对称轴为直线_______.
10.已知二次函数的图像在对称轴的左侧部分是上升的,那么m的取值范围是_______.
11.如图,已知在中,,CD是边AB上的高,如果,,那么_______.
12.如图,在中,,点D和点E在边BC上,,,那么_______.
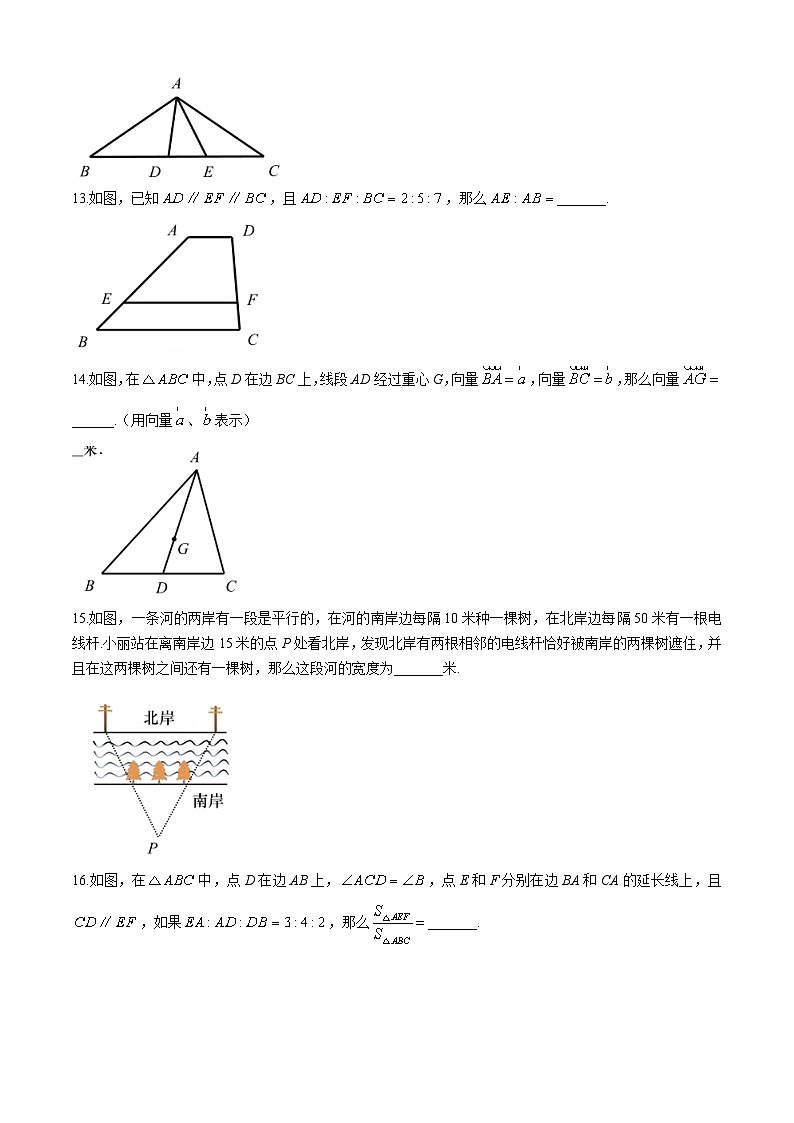
13.如图,已知,且,那么_______.
14.如图,在中,点D在边BC上,线段AD经过重心G,向量,向量,那么向量______.(用向量、表示)
15.如图,一条河的两岸有一段是平行的,在河的南岸边每隔10米种一棵树,在北岸边每隔50米有一根电线杆.小丽站在离南岸边15米的点P处看北岸,发现北岸有两根相邻的电线杆恰好被南岸的两棵树遮住,并且在这两棵树之间还有一棵树,那么这段河的宽度为_______米.
16.如图,在中,点D在边AB上,,点E和F分别在边BA和CA的延长线上,且,如果,那么_______.
17.定义:如果将抛物线上的点的横坐标不变,纵坐标变为点A的横、纵坐标之和,就会得到一个新的点,我们把这个点叫做点A的“简朴点”,已知抛物线上一点B的简朴点是,那么该抛物线上点的简朴点的坐标为_______.
18.如图,在矩形ABCD中,,在边CD上取一点E,将沿直线BE翻折,使点C恰好落在边AD上的F处,的平分线与边AD交于点M,如果,那么_______.
三、解答题(本大题共7题,满分78分)
19.(本题满分10分)
如图,已知两个不平行的向量、,求作,满足.
(不要求写作法,但要保留作图痕迹,并指出所作图中表示结论的向量.)
20.(本题满分10分,第(1)小题5分,第(2)小题5分)
已知点在二次函数的图像上.
(1)求二次函数图像的对称轴和顶点坐标;
(2)将二次函数的图像先向左平移4个单位,再向上平移t个单位后图像经过点,求的值.
21.(本题满分10分,第(1)小题5分,第(2)小题5分)
已知二次函数的图像经过原点,顶点坐标为.
(1)求二次函数的解析式;
(2)如果二次函数的图像与x轴交于点A(不与原点重合),联结OP、AP,试判断的形状并说明理由.
22.(本题满分10分,第1小题5分,第2小题5分)
如图,已知在中,点D在边AC上,过点A作,交BD的延长线于点E,点F是BE延长线上一点,联结CF,如果.
(1)求证:;
(2)如果,,求的值.
23.(本题满分12分,第(1)小题5分,第(2)小题7分)
如图,在中,CD是AB边上的高,点E是边AC的中点,联结ED并延长交CB的延长线于点F,且.
(1)求证:;
(2)如果,求证:.
24.(本题满分12分,第(1)小题4分,第(2)小题4分,第(3)小题4分)
如图,在平面直角坐标系xOy中,二次函数的图像与x轴交于点,与y轴交于点.
(1)求该二次函数的解析式;
(2)如果点是二次函数图像对称轴上的一点,联结AD、BD,求的面积;
(3)如果点P是该二次函数图像上位于第二象限内的一点,且,求点P的横坐标.
25.(本题满分14分,第(1)小题4分,第(2)小题6分,第(3)小题4分)
如图,在矩形ABCD中,,,点E是射线DA上的一点,点F是边AB延长线上的一点,且.联结CE、EF,分别交射线DB于点O、点P,联结CF、CP.
(1)当点E在边AD上时,
①求证:;
②设,,求y关于x的函数解析式;
(2)过点E作射线DB的垂线,垂足为点Q,当时,请直接写出DE的长.
2024学年第一学期九年级数学学科期中考试卷2024.10
参考答案及评分说明
一、选择题:(本大题共6题,每题4分,满分24分)
1.B;2.A;3.C;4.D;5.D;6.C.
二、填空题:(本大题共12题,每题4分,满分48分)
7.;8.;9.;10.;11.;12.;
13.;14.;15.;16.;17.;18.
三、解答题:
(本大题共7题,其中第19—22题每题10分,第23、24题每题12分,第25题14分,满分78分)
19.解: ,
20.解:(1)∵点在二次函数的图像上,
∴把,代入,得.
解得.
∴二次函数的解析式为.
∴对称轴为直线.
顶点的坐标为.
(2)二次函数的解析式化为.
∵将二次函数的图像先向左平移4个单位,再向上平移t个单位,
∴平移后新二次函数的解析式为.
∵平移后图像经过点,
∴把,代入,得.
解得.
21.解:(1)∵二次函数图像的顶点坐标为,
∴设二次函数的解析式为.
∵二次函数的图像经过原点,
∴把,代入得..
解得.
∴这个二次函数的解析式为.
(2)∵二次函数的图像与x轴交于点A,
∴把,代入得,(舍去).
得点A的坐标为.
∴.
∵,,
∴.
∵,
∴是等腰直角三角形.
22.解:(1)∵,∴.
∵,∴.
∴∴.
(2)∵,,∴.
∵,∴.
∵,∴,∴.
23.证明:(1)∵,∴.
∵CD是AB边上的高,点E是边AC的中点,
∴在中.
又∵,∴.∴.
∵,∴.
∴.
(2)∵,∴.∴.
∵,∴
∴∴.
∵,∴.
∴.∴.
24.解:(1)∵二次函数的图像与x轴交于点,与y轴交于点,
得
解得.
∴二次函数的解析式为.
(2)∵点是二次函数图像对称轴上的一点,
又∵二次函数图像的对称轴为直线.
∴,点D坐标为.
设直线AB的表达式为.
∵直线AB经过,,得,解得,
∴直线AB的表达式为.
设抛物线的对称轴与直线AB交于点E,得点E坐标为.
∴.
∴.
(3)过点P作轴,垂足为H.
设点.
∴,.
∵,
又∵,∴.
∵,∴.
∴.∴.
∴(舍去),.
即点P的横坐标是.
25.解:(1)∵四边形ABCD是矩形,
∴,,
∵,∴.
∵,∴.
∵,∴.∴.
∴.
(2)∵,∴.
即.
∵,∴.
∴.
∴.
∵,∴.∴.
又∵且,
∴.∴.
∵,∴.
∴.
∴.
∵在中,,,∴.
同理可得.
∴∴.
(3)
.
相关试卷
这是一份2021-2022学年上海市普陀区九年级下学期数学期中试题及答案,共24页。试卷主要包含了填空题,解答题等内容,欢迎下载使用。
这是一份2021-2022学年上海市普陀区九年级下学期数学4月月考试题及答案,共24页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
这是一份上海市普陀区2023-2024学年九年级上学期月考数学试题,共6页。试卷主要包含了12,1千米)等内容,欢迎下载使用。









