湖南省长沙市长郡教育集团2024年中考三模数学试卷（解析版）

这是一份湖南省长沙市长郡教育集团2024年中考三模数学试卷（解析版），共17页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
1. 的绝对值是（ ）
A. B. ﹣C. D.
【答案】C
【解析】的绝对值是，
故选：C．
2. 下列垃圾分类标识的图案既是轴对称图形，又是中心对称图形的是（ ）
A. B.
C. D.
【答案】C
【解析】A．不是轴对称图形，也不是中心对称图形，故此选项不符合题意；
B．是轴对称图形，不是中心对称图形，故此选项不符合题意；
C．是轴对称图形，也是中心对称图形，故此选项符合题意；
D．不是轴对称图形，也不是中心对称图形，故此选项不符合题意，
故选：C．
3. 下列计算中，正确的是（ ）
A. B.
C. D.
【答案】A
【解析】因为，所以A正确；
因为，所以B不正确；
因为，所以C不正确；
因为，所以D不正确．
故选：A．
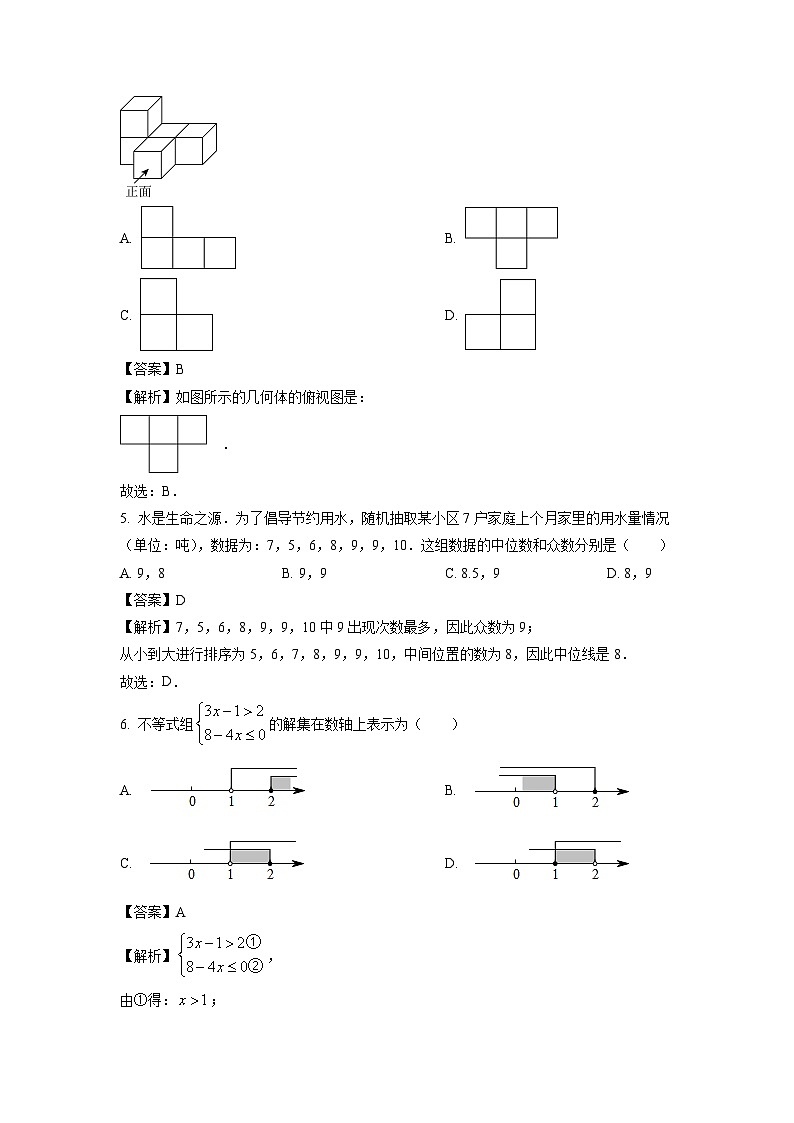
4. 如图所示的几何体是由5个完全相同的小正方体搭成的，它的俯视图是（ ）

A. B.
C. D.
【答案】B
【解析】如图所示的几何体的俯视图是：
．
故选：B．
5. 水是生命之源．为了倡导节约用水，随机抽取某小区7户家庭上个月家里的用水量情况（单位：吨），数据为：7，5，6，8，9，9，10．这组数据的中位数和众数分别是（ ）
A. 9，8B. 9，9C. 8.5，9D. 8，9
【答案】D
【解析】7，5，6，8，9，9，10中9出现次数最多，因此众数为9；
从小到大进行排序为5，6，7，8，9，9，10，中间位置的数为8，因此中位线是8．
故选：D．
6. 不等式组的解集在数轴上表示为（ ）
A. B.
C. D.
【答案】A
【解析】，
由①得：；
由②得：，
∴原不等组的解集为，；
在数轴上表示为
故选A．
7. 如图，直线，是直角三角形，，点C在直线n上．若，则的度数是（ ）

A. 60°B. 50°C. 45°D. 40°
【答案】D
【解析】延长交直线n于点D，如图所示．

∵，
∴．
在中，．故选：D．
8. 《孙子算经》中有一道题，原文是：今有木，不知长短，引绳度之，余绳四尺五寸；屈绳量之，不足一尺．木长几何？意思是：用一根绳子去量一根长木，绳子还剩余尺；将绳子对折再量长木，长木还剩余尺．问木长多少尺？设木长尺，绳长尺，根据题意列方程组得（ ）
A. B.
C. D.
【答案】A
【解析】设木长尺，绳长尺，根据题意列方程组得，
故选：A．
9. 如图，在平面直角坐标系中，已知点，，以原点O为位似中心，相似比为2，把放大，则点A的对应点的坐标是（ ）
A. B. 或
C. D. 或
【答案】D
【解析】∵以原点O为位似中心，相似比为2，把放大，点A的坐标为，
∴点A的对应点A′的坐标为或，即或，
故选：D．
10. 如图，在中，，分别以点和点为圆心，大于的长为半径作弧，两弧相交于，两点，作直线交，于点，，连接．下列说法错误的是（ ）
A. 直线是的垂直平分线B.
C. D.
【答案】D
【解析】A．由作图过程可知，直线是的垂直平分线，故选项正确，不符合题意；
B．由作图过程可知，直线是的垂直平分线，
∴点E是的中点，，
在中，，
∴，
∴，
即点D是的中点，
∴，
故选项正确，不符合题意；
C．∵点D是的中点，点E是的中点，
∴是的中位线，
∴，
故选项正确，不符合题意；
D．∵，
∴，
∴，
∴，
故选项错误，符合题意．
故选：D．
二、填空题（本大题共6个小题，每小题3分，共18分）
11. 若二次根式在实数范围内有意义，则x的取值范围是__________．
【答案】
【解析】由二次根式在实数范围内有意义可得： ，
解得： ；
故答案为 ．
12. 溶度积是化学中沉淀的溶解平衡常数．常温下的溶度积约为，将数据用科学记数法表示为__________________．
【答案】
【解析】．
故答案为：．
13. 一个七边形的内角和度数为______度．
【答案】900
【解析】七边形的内角和，
故答案为：900．
14. 抛物线的顶点坐标是______．
【答案】
【解析】抛物线的顶点坐标是，
故答案为：．
15. 在一个不透明的口袋中装有红球和白球共12个，这些球除颜色外都相同，将口袋中的球搅匀后，从中随机摸出1个球，记下它的颜色后再放回口袋中，不断重复这一过程，共摸球200次，发现有50次摸到红球，则口袋中红球约有________个．
【答案】
【解析】设红球有个，
则，
答：红球的个数约为个．
故答案为：．
16. 在一次数学活动课上，某数学老师将三张不同的牌分别发给甲、乙、丙三个同学，其中有一张牌是红桃A．
甲说：“红桃A在我手上”；
乙说：“红桃A不在我手上”；
丙说：“红桃A肯定不在甲手上”．
三个同学中只有一个说对了，则红桃A在______的手上．（填“甲”或“乙”或“丙”）
【答案】乙
【解析】由题意知，若甲正确，则乙正确，甲乙同学说法正确，故不符合要求；
若乙正确，甲错误，则红桃A在丙手上，则丙说法正确，乙丙同学说法正确，故不符合要求；
若丙正确，甲错误，乙错误，则红桃A在乙手上，
∴当三个同学中只有一个说对了，则红桃A在乙的手上，
故答案为：乙．
三、解答题（本大题共9个小题，第17、18、19题每题6分，第20、21题每题8分，第22、23题每题9分，第24、25题每题10分，共72分，解答应写出必要的文字说明、证明过程或演算步骤）
17. 计算：．
解：
．
18. 先化简，再求值：，其中．
解：原式
，
当时，原式．
19. 某风景区观景缆车路线如图所示，缆车从点出发，途经点后到达山顶，其中米，米，且段的运行路线与水平方向的夹角为，段的运行路线与水平方向的夹角为，求垂直高度．（结果精确到米，参考数据：，，）

解：过点作于，作于，则四边形矩形，

，
在中，，，
则（米），
米，
在中，，米，
则米，
米．
答：垂直高度约为米．
20. 某校为了调查本校学生对航空航天知识的知晓情况．开展了航空航天知识竞赛，从参赛学生中，随机抽取若干名学生的成绩进行统计，得到如下不完整的统计图表：

请根据图表信息解答下列问题：
（1）求a，b，c的值；
（2）补全频数直方图；
（3）某班有2名男生和1名女生的成绩都为100分，若从这3名学生中随机抽取2名学生参加演讲，用列表或画树状图的方法，求抽取的2名学生恰好为1男1女的概率．
解：（1）由题意得：抽取学生总数（人），
，
，
．
（2）补全频数分布直方图如图：

（3）画树状图如下：

共有6种等可能的结果，其中选出的2名学生恰好为一名男生、一名女生的结果有4种，
∴选出的2名学生恰好为一名男生、一名女生的概率为．
21. 如图，在中，点，分别在，的延长线上，且，连接与交于点，连接，．
（1）求证：；
（2）若，，求四边形的周长．
（1）证明：∵四边形是平行四边形
∴，（平行四边形的对边平行且相等）
∴（两直线平行，内错角相等）
∵
∴ 即
在和中，
∴；
（2）∵，
∴四边形是平行四边形（一组对边平行且相等的四边形是平行四边形）
又∵
∴是菱形（对角线互相垂直的平行四边形是菱形）
∴（菱形的四条边都相等）
∴菱形的周长.
22. 佳衣服装厂给某中学用同样的布料生产A，B两种不同款式的服装，每套A款服装所用布料的米数相同，每套B款服装所用布料的米数相同．若1套A款服装和2套B款服装需用布料5米，3套A款服装和1套B款服装需用布料7米．
（1）求每套A款服装和每套B款服装需用布料各多少米；
（2）该中学需要A，B两款服装共100套，所用布料不超过168米，那么该服装厂最少需要生产多少套B款服装？
解：（1）设每套A款服装需用布料x米，每套B款服装需用布料y米，
根据题意得：，
解得：．
答：每套A款服装需用布料米，每套B款服装需用布料米；
（2）设该服装厂需要生产m套B款服装，则需要生产套A款服装，
根据题意得：，
解得：，
∴m的最小值为60．
答：该服装厂最少需要生产60套B款服装．
23. 如图，以的边为直径作，交边于点D，过点C作交于点E，连接．

（1）求证：；
（2）若，求和的长．
（1）证明：，
，
，
，
，
；
（2）解：设，
是的直径，
，
，
，即，
根据（1）中的结论，可得，
根据勾股定理，可得，即，
解得，（舍去），
，,
根据勾股定理，可得；
解法一：如图，过点作的垂线段，交的延长线于点F，

，
，
，
，即，
，，，
，
，
，
设，则，
，
可得方程，解得，
，，
根据勾股定理，可得．
解法二：如图，连接,

，，
，
，
又，，，
，
．
24. 已知y是关于x的函数，若其图象经过点，则称点S为函数图象上的“双语点”．例如：直线上存在“双语点”．
（1）判断在下列关于x的函数中，是否存在“双语点”．存在的请在相应题目后的括号打“√”，不存在的请在相应题目后的括号打“×”；
①（ ）；②（ ）；③（ ）
（2）若抛物线上有两个“双语点”和，当时，求m的值；
（3）若关于x的函数的图象上存在两个“双语点”C和D，且同时满足①，②时，求线段CD长度L的取值范围．
解：（1）∵当时，，
∴存在“双语点”；
∵当时，方程无解，
∴不存在“双语点”；
∵当时，
，
，方程无解，
∴存在“双语点”；
故答案为：√，×，×；
（2）设抛物线“双语点”的坐标为，
将点S的坐标代入抛物线中得：
，
，
∵“双语点”为和，
∴、是方程的两个根，
则，，
，
∴，
∴，
又∵，
化简得：，，，（舍去），
综上所述；
（3）∵，∴，
∵，∴且，∴，
∵，∴，
∴，，
，
，
∵，
∴．
25. 如图1，为的外接圆，点B为的中点，点F为劣弧上除弧中点外一动点，连接，，连接交于D点，过F点作的切线交直线于E点．
（1）连接，则______，若，则的面积______；
（2）判断的形状，并进行证明；
（3）已知半径为r，如图2，取延长线上一点G，连接，且平分．
①求；（结果用r表示）
②是否为定值，若是请求出定值，若不是请说明理由．（结果用r表示）
解：（1）如图，过点O作，
∵点B为的中点，
∴，
∴，
∵，
∴，故为等边三角形，
∴，，
∴是的等腰三角形，，
，，
∴，
的面积；
（2）是等腰三角形．
理由如下：连接，延长交于点N，连接，
∵，，
∴是线段的垂直平分线，
∴，
∵是的切线，
∴，
∵，
∴，
∴，
∴；
（3）①连接，
由（2）得，，，
∵，
∴，
∴，
∴，
∵平分，
∴，
∴，
∵四边形是的内接四边形，
∴，
∵，且，
∴，
∵，
∴，
∴；
②为定值，理由如下：
设，，，
∴，，
∵平分，
∴点C到，的距离相等，设距离为h，
∴，
∵，
∴，即，整理得，即，
∴．成绩/分
频数/人
频率
10
0.1
15
b
a
0.35
40
c