人教版第一册上册函数的单调性课时练习

这是一份人教版第一册上册函数的单调性课时练习，共22页。试卷主要包含了增函数与减函数的定义，函数单调性的运算性质等内容，欢迎下载使用。


一.增函数与减函数
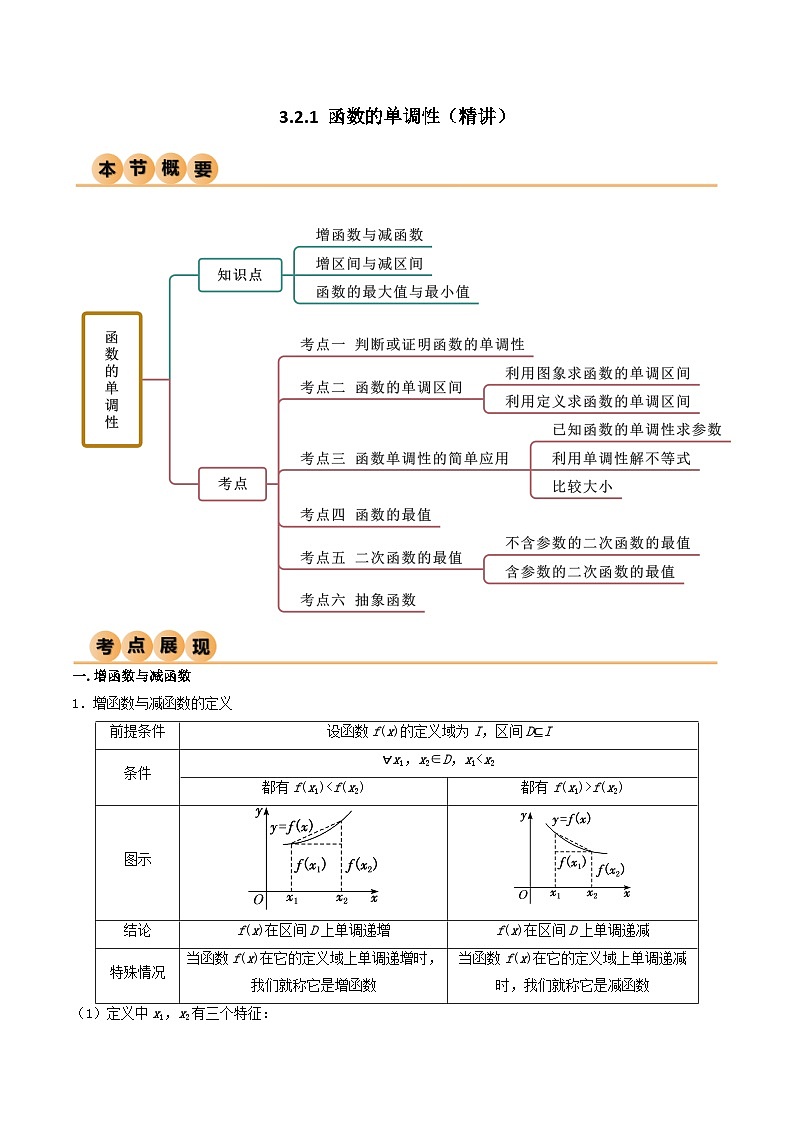
1．增函数与减函数的定义
（1）定义中x1，x2有三个特征：
一是x1，x2同属于一个单调区间；
二是x1，x2是任意的两个实数，证明单调性时不可随意用两个特殊值代替；
三是x1与x2有大小，通常规定x1＜x2，但也可规定x2＜x1.
(2)函数的递增(或递减)是针对定义域I内的某个区间D而言的，显然D⊆I.
(3)当函数值的改变量与其对应的自变量的改变量符号相同时，函数单调递增；符号相反时，函数单调递减．
(4)函数的单调区间是其定义域内的某一个区间，故讨论函数的单调性时，必须先确定函数的定义域.
(5)若函数在两个区间上都是单调递增(或递减)的，这两个单调区间不能用并集符号“∪”连接.
2．函数单调性的运算性质
若函数f(x)，g(x)在区间I上具有单调性，则在区间I上具有以下性质．
(1)f(x)与f(x)＋C(C为常数)具有相同的单调性．
(2)若a为常数，则当a＞0时，f(x)与af(x)具有相同的单调性；当a＜0时，f(x)与af(x)具有相反的单调性．Q
（3）在f(x)，g(x)的公共单调区间上，有如下结论：
二．函数的最大值与最小值
(1)最值首先是一个函数值，即存在一个自变量x0，使得f(x0)等于最值.
(2)对于定义域内的任意元素x，都有f(x)≤f(x0)(或f(x)≥f(x0))，“任意”两个字不可省略.
(3)使函数f(x)取得最大(小)值的自变量的值有时可能不止一个.
(4)函数f(x)在其定义域(某个区间)内的最大值的几何意义是其图象上最高点的纵坐标；最小值的几何意义是其图象上最低点的纵坐标.

一．利用定义证明函数单调性的步骤：
1.取值：设x1，x2是该区间内的任意两个值，且x12.作差变形：作差f(x1)－f(x2)，并通过因式分解、通分、配方、有理化等手段，转化为易判断正负的关系式；
3.定号：确定f(x1)－f(x2)的符号；
4.结论：根据f(x1)－f(x2)的符号与定义确定单调性.
二．常见函数的单调性
三．利用函数的单调性求最值的常用结论
1.若函数y＝f(x)在区间[a，b]上是增函数，则函数y＝f(x)在[a，b]上的最小值ymin＝f(a)，最大值ymax＝f(b)．
2.若函数y＝f(x)在区间[a，b]上是减函数，则函数y＝f(x)在[a，b]上的最小值ymin＝f(b)，最大值ymax＝f(a)．
3.若函数y＝f(x)在区间[a，b]上是增函数，在区间[b，c]上是减函数，则函数y＝f(x)，x∈[a，c]在x＝b处有最大值f(b)，最小值为f(a)与f(c)中的较小者．
4.若函数y＝f(x)在区间[a，b]上是减函数，在区间[b，c]上是增函数，则函数y＝f(x)，x∈[a，c]在x＝b处有最小值f(b)，最大值为f(a)与f(c)中的较大者．
四．求二次函数最值的常见类型及解法
1、类型一：是函数定义域为实数集R
法一：根据开口方向，用配方法即可求出最大(小)值
法二：根据开口和对称轴求出最值
2.类型二：定义域为某一区间----开口方向和对称轴的位置来决定
对于含参数的二次函数的最值问题，一般有如下几种类型：
(1)区间固定，对称轴变动(含参数)，求最值；
(2)对称轴固定，区间变动(含参数)，求最值；
(3)区间固定，最值也固定，对称轴变动，求参数.
通常都是根据区间端点和对称轴的相对位置进行分类讨论.
求二次函数f(x)＝ax2＋bx＋c(a＞0)在区间[m，n]上的最值一般分为以下几种情况：
①若x＝－eq \f(b,2a)在区间[m，n]内，则最小值为feq \b\lc\(\rc\)(\a\vs4\al\c1(－\f(b,2a)))，最大值为f(m)，f(n)中较大者(或区间端点m，n中与x＝－eq \f(b,2a)距离较远的一个对应的函数值为最大值)；
②若x＝－eq \f(b,2a)＜m，则f(x)在区间[m，n]上单调递增，最大值为f(n)，最小值为f(m)；
③若x＝－eq \f(b,2a)＞n，则f(x)在区间[m，n]上单调递减，最大值为f(m)，最小值为f(n)．
五．函数单调性应用
1.由函数解析式求参数
若为二次函数——判断开口方向与对称轴——利用单调性确定参数满足的条件．
若为一次函数——由一次项系数的正负决定单调性．
若为复合函数y＝|f(x)|或y＝f(|x|)——数形结合，探求参数满足的条件．
2.解不等式
当函数f(x)的解析式未知时，欲求解不等式，可以依据函数单调性的定义和性质，将符号“f”去掉，列出关于自变量的不等式(组)，然后求解，此时注意函数的定义域．
3.比较大小
利用函数的单调性可以比较函数值或自变量的大小，在解决比较函数值大小的问题时，需要自变量在同一个单调区间上，然后利用单调性比较大小
考点一 判断或证明函数的单调性
【例1】（2023·新疆乌鲁木齐）已知函数，判断并证明在上的单调性.
【答案】单调递增，证明见解析
【解析】函数在上单调递增.
证明：，任取，
，
因为，所以，，，
所以，即，
所以在上单调递增.
【一隅三反】
1．（2023·全国·高一假期作业）用定义证明：函数在上是增函数．
【答案】证明见解析
【解析】对任意，，
则，
因为，所以，
又，所以，故函数在上是增函数．
2．（2023·福建）求证：函数在区间上是减函数．
【答案】证明见解析
【解析】设，且，则,
，且，又，,
,即，故函数在区间是减函数.
3．（2023·云南）根据定义证明函数在区间上单调递增.
【答案】证明见解析
【解析】，，且，有
.
由，，得，，所以，，
又由，得，于是，即.
所以，函数在区间上单调递增.
考点二 函数的单调区间
【例2-1】（1）（2023·北京）函数，的单调减区间为（ ）
B．C．D．
（2）（2022·全国·高一专题练习）函数的单调增区间为（ ）
A．（0，+∞）B．（﹣∞，0）
C．（﹣∞，0）∪（0，+∞）D．（﹣∞，0），（0，+∞）
（3）（2023·天津和平）函数的单调递减区间为（ ）
A．B．C．D．，
（4）．（2023·全国·高一假期作业）已知的图象如图所示，则该函数的单调增区间为（ ）
A．B．和
C．D．和
（5）（2023春·高一校考开学考试）函数的单增区间为（ ）
A．B．
C．D．
【答案】（1）D（2）D（3）D（4）B（5）D
【解析】（1）函数对称轴为，开口向上，所以函数，的单调减区间为.故选：D
（2）∵函数1，定义域为{x|x≠0}，且y的单调递减区间为（﹣∞，0），（0，+∞），
故函数的单调增区间为（﹣∞，0），（0，+∞），故选：D．
（3）函数为对勾函数，由对勾函数的性质知，函数的单调递减区间为：，.
不能选C，因为不满足减函数的定义.故选：D.
（4）由图象知：该函数的单调增区间为和.故选：B
（5）.因为，，
所以的增区间是．故选：D
【一隅三反】
1．（2023·全国·高一假期作业）下列命题正确的是（ ）
A．函数在上是增函数B．函数在上是减函数
C．函数和函数的单调性相同D．函数和函数的单调性相同
【答案】C
【解析】对于A：定义域为，由二次函数的图像可知，在是增函数，在是减函数，故A错误；
对于B：的定义域为，由反比例函数的图像可知，在和上是减函数，故B错误；
对于C：在是增函数，在是减函数，
，当时，，易知为增函数，当时，，易知为减函数，所以函数和函数的单调性相同，故C正确；
对于D：定义域为，由反比例函数的图像可知，在和上是减函数；
设定义域为，取，
则，
当时，，即在上单调递减，
当，，即在上单调递减，
同理可证，在上单调递减，在上单调递增，故D错误，
故选：C．
2．（2023·浙江温州）函数单调减区间是___________.
【答案】
【解析】由，
如图所示：
由图可知函数单调减区间是：，
故答案为：.
3．（2023·全国·高一假期作业）已知函数，则的单调递增区间为__________.
【答案】
【解析】当时，单调递减；
当时，，在上单调递增，在单调递减；
故答案为：
4．（2023·上海杨浦）函数的单调减区间为___________.
【答案】和
【解析】，由于函数的单调减区间为和.
故函数的单调减区间为和.故答案为：和
考点三 函数单调性的应用
【例3-1】（1）（2023·北京）设函数是上的减函数，则有（ ）
A．B．C．D．
（2）（2023·全国·高一专题练习）“”是“函数在区间上为减函数”的（ ）
A．充分不必要条件B．必要不充分条件
C．充要条件D．既不充分也不必要条件
（3）（2023安徽芜湖）已知函数满足对任意的实数都有成立，则实数的取值范围为（ ）
A．B．C．D．
【答案】（1）D（2）A（3）B
【解析】由题意函数是上的减函数，
则，否则为常数函数，不合题意，故为一次函数，
故，故选：D
（2）的图象如图所示，要想函数在区间上为减函数，必须满足，
因为是的子集，所以“”是“函数在区间上为减函数”的充分不必要条件.
故选：A
（3）由函数满足对任意的实数都有成立，所以在上单调递减，
由题意，得，解得，故选：B．
【例3-2】（1）（2023·高一课时练习）函数的定义域为，且在定义域内是增函数，若，则m的取值范围是（ ）
A．B．C．D．
（2）（2023·江西抚州）已知函数，则不等式的解集为（ ）
A．B．或C．D．
【答案】（1）C（2）D
【解析】因为，所以，
又函数的定义域为，且在定义域内是增函数，
所以有，解得.故选：C
（2）函数中，
在上单调递减，在上单调递减，且，
则函数在定义域上单调递减，
，，解得：，
即不等式的解集为.故选：D.
【例3-3】（2023·福建）已知函数是区间内的减函数，则与的大小关系为（ ）
A．B．
C．D．不确定
【答案】B
【解析】因为，又是区间内的减函数，所以.
故选：B．
【一隅三反】
1．（2023·湖南常德）若函数在上单调递增,则a的取值范围是( )
A．B．C．D．
【答案】D
【解析】当时，则，在上单调递增，满足题意；
当时，的对称轴为，
要使函数在上单调递增，只需，解得
综上，a的取值范围是故选：D
2．（2022·广东梅州）已知函数在上单调，则实数k的取值范围为（ ）
A．B．C．D．
【答案】D
【解析】的对称轴为，
若在上单调递增，则，解得，
若在上单调递减，则，解得，
所以实数k的取值范围为.
故选：D.
3．（2022秋·四川广安·高一统考期末）已知函数在上单调递增，则实数a的取值范围为（ ）
A．B．
C．D．
【答案】C
【解析】由题意，，在中，函数单调递增，
∴，解得：，故选：C.
4．（2023·高一课时练习）己知是函数的增区间，则下列结论成立的是（ ）
A．B．C．D．
【答案】A
【解析】因为是函数的增区间，所以，故A正确；
由于无法确定、的取值情况，故无法判断的符号，故B、C、D错误；
故选：A
5．（2023·全国·高一假期作业）设函数满足：对任意的都有，则与大小关系是 （ ）
A．B．
C．D．
【答案】A
【解析】因为，当时；当时；
所以函数在实数上单调递增，又，所以.
故选：A
6．（2023·全国·高一假期作业）已知是定义在上的减函数，则不等式的解集为________.
【答案】
【解析】因为是定义在上的减函数，则，可得，故解集为.
故答案为：
考点四 函数的最值
【例4-1】（2023·北京）函数在区间[1，2]上的最大值与最小值分别是（ ）
A．B．2，5C．1，2D．
【答案】A
【解析】∵y＝x2+1在（0，+∞）上单调递增，且y＞1，
∴在区间[1，2]上单调递减，
∴函数在区间[1，2]上的最大值与最小值分别是
f（1），f（2），
故选：A．
【例4-2】（2022秋·高一单元测试）当时，则函数的值域为（ ）
A．B．
C．D．
【答案】C
【解析】令，因为，所以，
当时，函数单调递减，故，
当时，即，所以，
所以函数的值域为：.故选：C．
【例4-3】（2023·内蒙古通辽）已知函数的最大值为m，的最小值为n，则______．
【答案】
【解析】当时，，
所以此时，
当时，，
所以此时，
综上所述，，即，
所以.故答案为：.
【一隅三反】
1．（2023春·云南普洱）函数的最小值为（ ）
A．2B．C．3D．以上都不对
【答案】B
【解析】令，则，
因为在上单调递增，所以当时取得最小值，故选：B
2．（2022秋·天津和平）设函数，则的值域是（ ）
A．B．
C．D．
【答案】D
【解析】当,即，时,或,
,
因为，所以，因此这个区间的值域为.
当时,即，得,
其最小值为，其最大值为，因此这区间的值域为.
综上，函数值域为:.故选：D
3．（2022秋·新疆·高一乌鲁木齐市第70中校考期中）若函数的值域是，则实数的取值范围是 __．
【答案】
【解析】因为函数.
当时，有，当且仅当时等号成立.
当，即时，有，不满足题意；
当，即时，在上单调递减，有，不满足题意；
当，即时，在上单调递增，有.
要使的值域是，则应有，所以.
综上所述，当时，的值域是.
故答案为：.
考点五 二次函数的最值
【例5】（2023·广东）已知函数.
(1)求的最小值;
(2)求的最大值.
【答案】(1)
(2)2
【解析】（1）由题意可得：，
当时，在区间上单调递减，最小值；
当时，在区间上单调递减，在区间上单调递增，最小值；
当时，在区间上单调递增，最小值；
综上所述：.
（2）由（1）可知：当时，在单调递减，所以的最大值为；
当时，在区间上单调递增，在区间上单调递减，所以的最大值为；
当时，在单调递增，所以的最大值为；
综上所述：的最大值.
【一隅三反】
1．（2023·上海闵行）已知函数严格单调，且的最大值为8，求实数的值.
【答案】
【解析】，对称轴为，开口向上，
当时，在上单调递增，
故当时，取得最大值，，解得：，满足，
当时，在上单调递减，在上单调递增，
且，所以当时，取得最大值，
由，解得：，与矛盾，舍去；
当时，在上单调递减，在上单调递增，
且，所以当时，取得最大值，
由，解得：，与矛盾，舍去；
当时，在上单调递减，
故当时，取得最大值，，解得：，与矛盾，舍去；
综上：.
2．（2022秋·云南·高一校联考阶段练习）已知二次函数，非空集合.
(1)当时，二次函数的最小值为，求实数的取值范围；
(2)当__________时，求二次函数的最值以及取到最值时的取值.
在①，②，③，这三个条件中任选一个补充在（2）问中的横线上，并求解.
（注：如果选择多个条件分别解答，按第一个解答计分.）
【答案】(1)；
(2)见解析．
【解析】（1），
由于当且仅当时，才可取到最小值，
于是，即.
（2）根据二次函数的性质，在上单调递减，在上单调递增，
于是当时，最小值一定在取得，最大值在或处取得.
选择方案①，
当时，在上递减，
，此时，
，此时．
选择方案②，
当时，，此时或，
，此时．
选择方案③，
当时，，，此时，
，此时．
3．（2023秋·云南红河·高一统考期末）已知函数.
(1)当时，求的解集；
(2)求函数在区间上的最小值.
【答案】(1)
(2)
【解析】（1）当时， 不等式，即，解得.
所以不等式的解集为.
（2）易知的对称轴为，则
①当时，在上单调递增，则.
②当时，在上单调递减，在上单调递增，则
③当时，在上单调递减，则
综上.
考点六 抽象函数
【例6】（2023·江西抚州）已知函数的定义域为,且对任意的正实数都有,且当时,,.
(1)求;
(2)求证:为上的增函数;
(3)解不等式.
【答案】(1)
(2)证明见解析
(3)
【解析】（1）因为,,
令,则,解得,
令,则,
令,,则,
所以.
（2）设,
因为当时,,则,
令,则,即,
所以,
根据单调性定义,为上的增函数.
（3）因为在上为增函数,
又,
所以,解得,
即原不等式的解集为.
【一隅三反】
1．（2023·江苏·高一假期作业）已知函数对任意的，都有，且当时，．
(1)求证：是上的增函数；
(2)若，解不等式．
【答案】(1)证明见解析
(2)
【解析】（1）设，且，
则，即，
所以，
所以，所以是上的增函数．
（2）因为，所以．
在上式中取，则有，
因为，所以．
于是不等式等价于．
又由（1）知是上的增函数，
所以，解得或，
所以原不等式的解集为．
2．（2023·重庆沙坪坝）已知定义在的函数满足以下条件：
①；
②当时，；
③对，均有．
(1)求和的值；
(2)判断并证明的单调性；
(3)求不等式的解集．
【答案】(1)，；
(2)在上单调递增，证明见解析；
(3).
【解析】（1）因为，，
所以令，则，
令，则，
令，则，即，
得或，
令，则，即，
若，则，与已知矛盾，
所以；
（2）在上单调递增，证明如下：
任取，且，则
，
所以，
则
，
令，则，
所以，
当时，，所以，
所以，则，
所以，即，
所以当时，，
所以，
因为，
所以，即，
所以在上单调递增；
（3）由（2）可知当时，，所以，
所以可化为，
所以，所以，所以，
因为在上单调递增，所以，
令，则在上单调递增，
因为，所以可化为，所以，
即原不等式的解集为.
前提条件
设函数f(x)的定义域为I，区间D⊆I
条件
∀x1，x2∈D，x1都有f(x1)都有f(x1)>f(x2)
图示
结论
f(x)在区间D上单调递增
f(x)在区间D上单调递减
特殊情况
当函数f(x)在它的定义域上单调递增时，我们就称它是增函数
当函数f(x)在它的定义域上单调递减时，我们就称它是减函数
f(x)
g(x)
f(x)＋g(x)
f(x)－g(x)
增
增
增
不能确定单调性
增
减
不能确定单调性
增
减
减
减
不能确定单调性
减
增
不能确定单调性
减
最大值
最小值
条件
一般地，设函数y＝f(x)的定义域为I，如果存在实数M满足：∀x∈I，都有
f(x)≤M
f(x)≥M
∃x0∈I，使得f(x0)＝M
结论
称M是函数y＝f(x)的最大值
称M是函数y＝f(x)的最小值
几何意义
f(x)图象上最高点的纵坐标
f(x)图象上最低点的纵坐标
函数
单调性
一次函数y＝ax＋b(a≠0)
a＞0时，在R上单调递增；
a＜0时，在R上单调递减
反比例函数y＝eq \f(a,x)(a≠0)
a＞0时，减区间是(－∞，0)和(0，＋∞)；
a＜0时，增区间是(－∞，0)和(0，＋∞)
二次函数y＝a(x－m)2＋n(a≠0)
a＞0时，减区间是(－∞，m]，增区间是[m，＋∞)；
a＜0时，减区间是[m，＋∞)，增区间是(－∞，m]