

高中数学函数的奇偶性同步练习题
展开一.函数的奇偶性
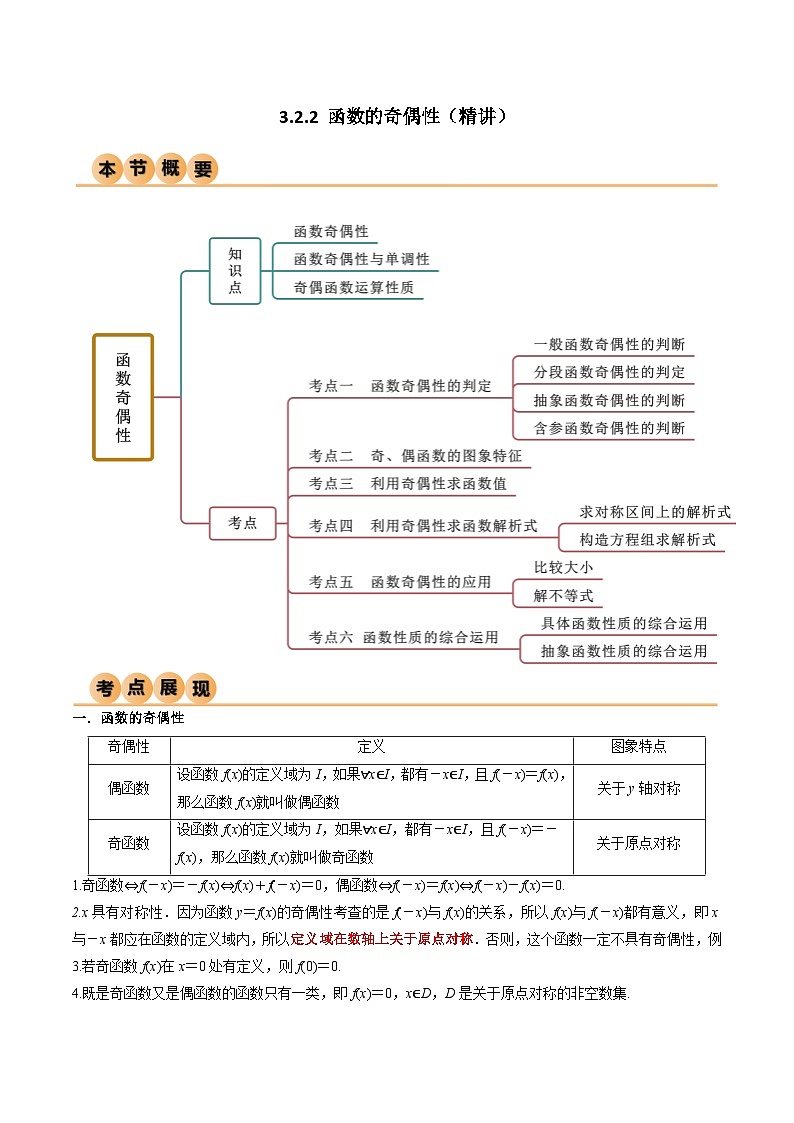
1.奇函数⇔f(-x)=-f(x)⇔f(x)+f(-x)=0,偶函数⇔f(-x)=f(x)⇔f(-x)-f(x)=0.
2.x具有对称性.因为函数y=f(x)的奇偶性考查的是f(-x)与f(x)的关系,所以f(x)与f(-x)都有意义,即x与-x都应在函数的定义域内,所以定义域在数轴上关于原点对称.否则,这个函数一定不具有奇偶性,例
3.若奇函数f(x)在x=0处有定义,则f(0)=0.
4.既是奇函数又是偶函数的函数只有一类,即f(x)=0,x∈D,D是关于原点对称的非空数集.
二.函数的奇偶性与单调性
1.若f(x)为奇函数且在区间[a,b](a
在公共定义域内:
1.两个奇函数的和函数是奇函数,两个奇函数的积函数是偶函数;
2.两个偶函数的和函数、积函数都是偶函数;
3.一个奇函数、一个偶函数的积函数是奇函数.
四.函数的对称轴与对称中心(拓展)
(1)若函数f(x)的定义域为D,对∀x∈D都有f(T+x)=f(T-x)(T为常数),则x=T是f(x)的对称轴.
(2)若函数f(x)的定义域为D,对∀x∈D都有f(a+x)+f(a-x)=2b(a,b为常数),则(a,b)是f(x)的对称中心.
一.判断函数奇偶性的方法
1.定义法:一求二看三判断
2.图象法
3.性质法
设f(x),g(x)的定义域分别是D1,D2,那么在它们的公共定义域上:奇+奇=奇,奇×奇=偶,偶+偶=偶,偶×偶=偶,奇×偶=奇.
4.分段函数奇偶性的判断,要分别从x>0或x<0来寻找等式f(-x)=f(x)或f(-x)=-f(x)成立,只有当对称的两个区间上满足相同关系时,分段函数才具有确定的奇偶性.
二.利用奇偶性求解析式
1.求哪个区间上的解析式,x就设在那个区间上;(2)把x对称转化到已知区间上,代入到已知区间上的函数解析式中;
2.利用f(x)的奇偶性将f(-x)用-f(x)或f(x)表示,从而求出f(x).
三.利用函数奇偶性和单调性解不等式
1.利用图象解不等式.
2.转化为简单不等式求解.
(1)利用已知条件,结合函数的奇偶性,把已知不等式转化为f(x1)<f(x2)或f(x1)>f(x2)的形式;
(2)根据奇函数在对称区间上的单调性一致,偶函数在对称区间上的单调性相反,去掉不等式中的“f”转化为简单不等式(组)求解.
注意:列不等式(组)时不要忘掉函数定义域.
四.比较大小的
1.在同一单调区间上,直接利用函数的单调性比较大小.
2.不在同一单调区间上,需利用函数的奇偶性把自变量转化到同一单调区间上,然后利用单调性比较大小.
五.函数的周期性、奇偶性与单调性的综合应用
函数周期性的概念:对于函数f(x),如果存在一个非零常数T,使得定义域内的每一个x值都满足f(x+T)=f(x),那么函数f(x)就叫作周期函数,非零常数T叫作这个函数的周期,T的最小正数取值称为函数f(x)的最小正周期.
考点一 函数奇偶性的判断
【例1-1】(2023·山西)判断下列函数的奇偶性:
; (2) ; (3).
(4); (5)
【一隅三反】
1.(2023春·上海宝山)函数的奇偶性为( )
A.奇函数B.偶函数C.非奇非偶函数D.既奇又偶函数
2.(2023·高一课时练习)函数的奇偶性是( )
A.奇函数B.偶函数C.非奇非偶函数D.既奇又偶函数
3.(2023·北京)下列函数中,是偶函数的是( )
A.B.C.D.
4.(2023·天津滨海)下列判断正确的是( )
A.是奇函数B.是偶函数
C.是偶函数D.既是奇函数又是偶函数
5.(2023·全国·高一假期作业)对于两个定义域关于原点对称的函数和在它们的公共定义域内,下列说法中正确的是( )
A.若和都是奇函数,则是奇函数
B.若和都是偶函数,则是偶函数
C.若是奇函数,是偶函数,则是偶函数
D.若和都是奇函数,则不一定是奇函数
考点二 奇偶函数的图像特征
【例2】(2022秋·安徽马鞍山)已知定义在R上的函数是奇函数,且当时,.
(1)求和的值;
(2)求函数的解析式;
(3)作函数的图象,并写出它的单调区间和值域.
【一隅三反】
1.(2023春·上海金山·高一统考阶段练习)已知.
(1)判断并证明函数的奇偶性;
(2)判断并证明函数在区间上的单调性;
(3)根据函数的性质,画出函数的大致图像.
2.(2023·河南三门峡·高一统考期末)已知函数的图象关于原点对称,且当时,.
(1)试求在上的解析式;
(2)画出函数的图象,根据图象写出它的单调区间.
3.(2022秋·福建福州·高一校联考期中)已知函数是定义在R上的偶函数,如图所示,现已画出函数在y轴左侧的图象,
(1)请画出y轴右侧的图像,并写出函数的解析式和单调减区间;
(2)若函数,求函数的最大值.
考点三 利用奇偶性求函数值
【例3-1】(2023春·云南红河)已知函数是定义在上的奇函数,当时,,则___.
【例3-2】(2023·广东)已知函数,且,则______.
【一隅三反】
1.(2023·全国·高一假期作业)已知是上的奇函数,当时,,则( )
A.4B.C.7D.
2.(2023·全国·高一假期作业)已知是定义在上的奇函数,且,则的值为( )
A.1B.2C.3D.4
3.(2023·湖南)已知函数,且,则______.
考点四 利用奇偶性求函数解析式
【例4-1】(2022秋·江西景德镇·高一统考期中)若是上的奇函数,且当时,,则当,______.
【例4-2】(2023·广西)已知函数是定义在R上的偶函数,当时,,则函数在R上的表达式为______.
【一隅三反】
1.(2023·重庆璧山)已知函数在上为偶函数,且当时,,则当时,的解析式是( )
A.B.
C.D.
2.(2023·全国·高一假期作业)已知是定义域为R的奇函数,当时,,则当时,的表达式为_________.
3.(2023·山东)已知奇函数则__________.
考点五 函数奇偶性的应用
【例5-1】(2022秋·江西宜春·高一校考阶段练习)设是定义在上偶函数,则在区间上是( )
A.增函数B.减函数C.先增后减函数D.与,有关,不能确定
【例5-2】(2023安徽)定义在上的偶函数满足:对任意的,有,则、、的大小关系为( )
A.B.
C.D.
【例5-3】(2023春·河南)已知函数为定义在上的奇函数,且当时,则关于的不等式的解集为( )
A. B.
C. D.
【例5-4】(2023春·江苏扬州·高一统考开学考试)已知是定义在上的偶函数,对于任意的,(),都有成立.若,则实数m的取值范围为( )
A.或B.
C.或 D.
【一隅三反】
1.(2023·江苏盐城)设是定义在上的奇函数,则=( )
A.B.C.D.
2.(2023福建)已知是奇函数且对任意正实数,恒有,则下列结论一定正确的是( )
A.B.
C.D.
3.(2023秋·高一单元测试)设偶函数 在区间 上单调递增, 则( )
A.B.
C.D.
4.(2023·广东深圳)定义在上的偶函数在单调递减,则不等式的解集是( )
A.B.C.D.
5.(2022秋·高一课时练习)若函数在上是偶函数,在上单调递增,则,,的大小关系是___________.
6.(2023·贵州黔西·高一统考期末)已知定义域为的函数是奇函数且.若对于任意,不等式恒成立,则的取值范围为_______.
考点六 函数性质的综合运用
【例6-1】(2023·北京)函数是定义在上的奇函数,且.
(1)确定的解析式;
(2)判断在上的单调性,并证明你的结论;
(3)解关于的不等式.
【例6-2】(2023春·广西南宁·高一校联考开学考试)设函数是定义在上的增函数,对于任意都有.
(1)证明是奇函数;
(2)解不等式.
【一隅三反】
1.(2023·江苏苏州)已知函数是定义在上的奇函数,且.
(1)求函数的解析式;
(2)判断在上的单调性,并用单调性定义证明;
(3)解不等式.
2.(2023·陕西渭南)已知二次函数.
(1)若函数是偶函数,求实数的值;
(2)是否存在实数,使得函数在上的值域也是?若存在,求出的值;若不存在,请说明理由.
3.(2023秋·高一单元测试)已知函数y=f(x)的定义域为R,且对任意a,b∈R,都有f(a+b)=f(a)+f(b),且当x>0时,f(x)<0恒成立.
(1)证明函数y=f(x)是R上的单调函数;
(2)讨论函数y=f(x)的奇偶性;
(3)若f(x2-2)+f(x)<0,求x的取值范围.
奇偶性
定义
图象特点
偶函数
设函数f(x)的定义域为I,如果∀x∈I,都有-x∈I,且f(-x)=f(x),那么函数f(x)就叫做偶函数
关于y轴对称
奇函数
设函数f(x)的定义域为I,如果∀x∈I,都有-x∈I,且f(-x)=-f(x),那么函数f(x)就叫做奇函数
关于原点对称
数学第一册上册对数练习: 这是一份数学第一册上册<a href="/sx/tb_c9535_t7/?tag_id=28" target="_blank">对数练习</a>,共8页。试卷主要包含了对数的概念,常用对数与自然对数,1B.8等内容,欢迎下载使用。
高中数学人教版第一册上册第二章 函数指数函数综合训练题: 这是一份高中数学人教版第一册上册<a href="/sx/tb_c9541_t7/?tag_id=28" target="_blank">第二章 函数指数函数综合训练题</a>,共10页。试卷主要包含了定义,具有三个特征,解指数型不等式,与指数函数复合的函数单调性等内容,欢迎下载使用。
高中人教版指数同步训练题: 这是一份高中人教版<a href="/sx/tb_c9536_t7/?tag_id=28" target="_blank">指数同步训练题</a>,共8页。试卷主要包含了a的n次方根的定义,a的n次方根的表示,根式,eq \r=a等内容,欢迎下载使用。













