数学指数函数当堂达标检测题

这是一份数学指数函数当堂达标检测题，共19页。试卷主要包含了定义，具有三个特征，解指数型不等式，与指数函数复合的函数单调性等内容，欢迎下载使用。


一．指数函数的概念
1.定义：一般地，函数y＝ax(a>0，且a≠1)叫做指数函数，其中指数x是自变量，定义域是R.
2.具有三个特征：
(1)底数a为大于0且不等于1的常数；(2)指数位置是自变量x；(3)ax的系数是1.
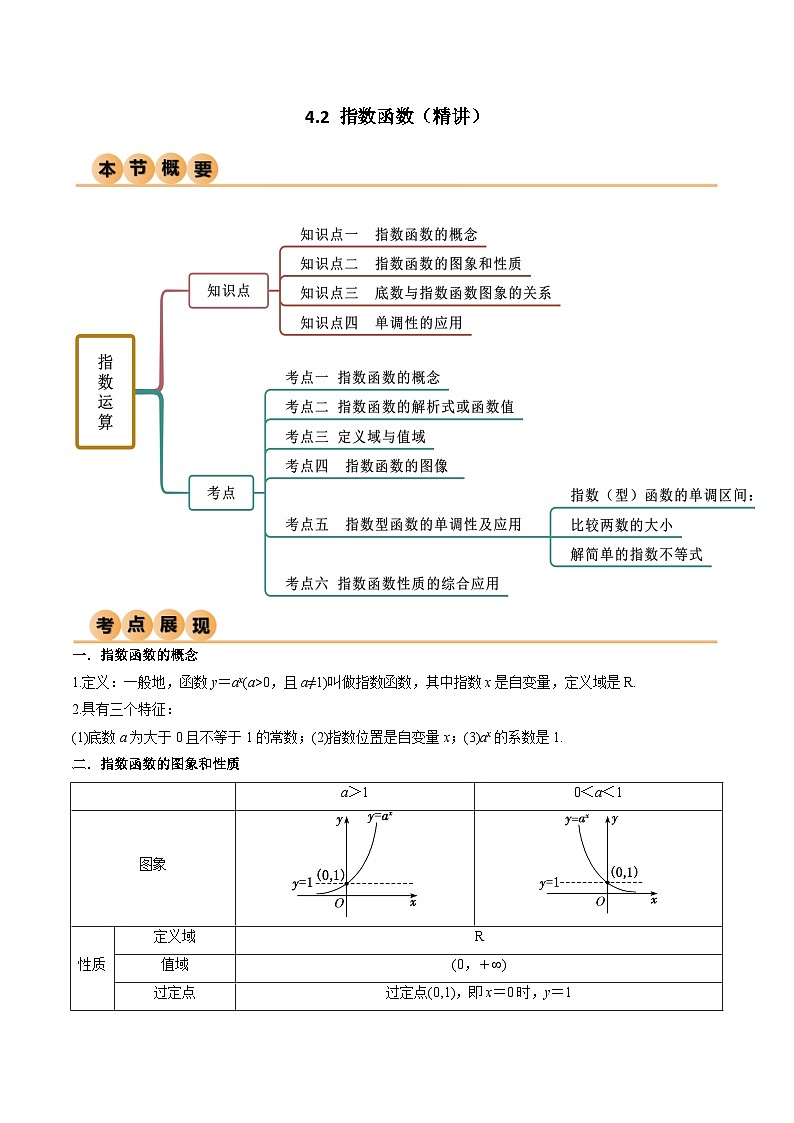
二．指数函数的图象和性质
三．底数与指数函数图象的关系
1.由指数函数y＝ax的图象与直线x＝1相交于点(1，a)可知在y轴右侧，图象从下到上相应的底数由小变大．
2.由指数函数y＝ax的图象与直线x＝－1相交于点eq \b\lc\(\rc\)(\a\vs4\al\c1(－1，\f(1,a)))可知，在y轴左侧，图象从下到上相应的底数由大变小．如图所示，指数函数底数的大小关系为0＜a4＜a3＜1＜a2＜a1.
四．单调性的应用
3.解指数型不等式
(1)形如af(x)>ag(x)的不等式，可借助y＝ax的单调性求解；
(2)形如af(x)>b的不等式，可将b化为以a为底数的指数幂的形式，再借助y＝ax的单调性求解；
(3)形如ax>bx的不等式，可借助两函数y＝ax，y＝bx的图象求解.
4.与指数函数复合的函数单调性
一般地，形如y＝af(x)(a>0，且a≠1)函数的性质有：
(1)函数y＝af(x)与函数y＝f(x)有相同的定义域.
(2)当a>1时，函数y＝af(x)与y＝f(x)具有相同的单调性；当0一．函数图象
1.抓住特殊点：指数函数的图象过定点(0，1)，求指数型函数图象所过的定点时，只要令指数为0，求出对应的y的值，即可得函数图象所过的定点.
2.巧用图象变换：函数图象的平移变换(左右平移、上下平移).
3.利用函数的性质：奇偶性与单调性.
4.在y轴右侧，图象从上到下相应的底数由大变小，即“底数大图象高”；
在y轴左侧，图象从上到下相应的底数由小变大，即“底数大图象低”.
二.y＝af(x)型函数的定义域、值域的求法
(1)形如y＝af(x)的函数的定义域就是f(x)的定义域.
(2)形如y＝af(x)的函数的值域，先求出u＝f(x)的值域，再结合y＝au的单调性求出y＝af(x)的值域.若a的取值范围不确定，则需对a进行分类讨论.
2.y＝f(ax)型函数的定义域、值域的求法
三．比较指数幂大小的常用方法
1.底数相同，指数不同：利用指数函数的单调性来判断
2.底数不同，指数相同：利用底数不同的指数函数的图象的变化规律来判断或者按幂函数性质判断
3.底数不同，指数不同：通过中间量来比较
考点一 指数函数的概念
【例1-1】（2023秋·高一课时练习）下列函数：①；②；③；④．其中为指数函数的个数是（ ）
A．B．
C．D．
【答案】B
【解析】指数函数解析式为且，
对于①②④，、和不符合指数函数解析式特征，①②④错误；
对于③，符合指数函数解析式特征，③正确.
故选：B.
【例1-2】（2023秋·吉林长春·高一长春外国语学校校考期末）若函数是指数函数，则等于（ ）
A．或B．C．D．
【答案】C
【解析】因为函数是指数函数，
所以.故选：C
【一隅三反】
1．（2023·全国·高一课堂例题）下列函数为指数函数的是（ ）
A．B．C．D．
【答案】C
【解析】根据指数函数的定义知，
可得函数不是指数函数；函数不是指数函数；
函数是指数函数；函数不是指数函数.
故选：C.
2．（2023秋·高一课时练习）（多选）下列函数是指数函数的是（ ）
A．
B．
C．
D．（且）
【答案】AD
【解析】对于A选项，为指数函数；
对于B选项，不是指数函数；
对于C选项，不是指数函数；
对于D选项，当且时，且，
则（且）为指数函数.
故选：AD.
3．（2023·全国·高一假期作业）（多选）下列函数中，是指数函数的是（ ）
A．B．
C．D．
【答案】BC
【解析】由指数函数形式为且，显然A、D不符合，C符合；
对于B，且，故符合.故选：BC
考点二 指数函数的解析式与函数值
【例2】（2023春·新疆）指数函数且图像经过点，则（ ）
A．3B．6C．9D．12
【答案】C
【解析】由题意，得，故，
故选：C
【一隅三反】
1．（2023·全国·高一专题练习）函数，且的图象经过点，则（ ）
A．B．C．D．9
【答案】D
【解析】由题意可知，，，且，得，
所以，.
故选：D
2．（2023秋·高一课时练习）若指数函数的图象经过点，则 ．
【答案】/
【解析】设指数函数且，
过点，，解得：，，
.
故答案为：.
3．（2023春·贵州黔东南·高一校考期末）已知指数函数的图像经过点，则 ．
【答案】/0.5
【解析】设（，且），由于其图像经过点 ，
所以，解得或（舍去），
因此，故 .故答案为：.
考点三 定义域与值域
【例3-1】（2023秋·高一课前预习）求下列函数的定义域：
（1）；（2）.
【答案】（1）；（2）.
【解析】（1）由题意可得，即，又指数函数单调递增，得.
所以函数的定义域为；
（2）由题意，得，得，
又指数函数单调递减，且.
所以函数的定义域为.
【例3-2】（2023秋·江西）求下列函数的值域；
(1)； (2)； (3).
【答案】(1)(2)(3)
【解析】（1）的定义域为R，值域为；
（2）由知，故的定义域为；
由知，故的值域为；
（3）的定义域为；由知，故的值域为.
【例3-3】（2023·全国·高三专题练习）已知函数的值域为R，则实数a的取值范围是（ ）
A．B．C．D．
【答案】D
【解析】当时，，当时， ，
因为函数的值域为，所以，得，
所以实数的取值范围是，故选：D.
【一隅三反】
1．（2023秋·高一课时练习）函数 的定义域是（ ）
A．B．
C．D．
【答案】C
【解析】由题意得所以，即，
又指数函数为上的单调减函数，所以，解得.故选：C.
2．（2022秋·高一课时练习）函数的定义域为 .
【答案】
【解析】由题意可得，解得：，所以函数的定义域为.
故答案为：.
3．（2023秋·高一课时练习）函数的值域是 ．
【答案】
【解析】由函数值域为，则函数的值域为.故答案为：
4．（2023秋·高一单元测试）函数的值域为 ．
【答案】
【解析】因为函数在上是增函数，所以，
，故函数值域为：，故答案为：.
5．（2023·上海）已知，则的值域是 ；
【答案】
【解析】当 时, 根据指数函数的图象与性质知，
当 时, . 综上: 的值域为 .故答案为：.
6．（2023黑龙江）已知函数的值域为R，则a的取值范围是
【答案】
【解析】当时，，而函数在上单调递增，又是增函数，
因此函数在上单调递增，，即函数在上的值域为，
当时，函数的值域为，而函数的值域为R，因此，
而当时，，必有，解得，
所以a的取值范围是.
考点四 指数函数的图像
【例4-1】（2022春·北京）已知对不同的值，函数的图象恒过定点，则点的坐标是 .
【答案】
【解析】由指数函数的图象恒过点
而要得到函数的图象，
可将指数函数的图象向右平移1个单位，再向上平移2个单位.
则点平移后得到点.
则点的坐标是
故答案为：
【例4-2】（2023秋·高一单元测试）函数的图象如图所示，其中a，b为常数，则下列结论正确的是（ ）

A．B．
C．D．
【答案】D
【解析】由图象可知，函数为减函数，
从而有；
法一：由图象，函数与轴的交点纵坐标，
令，得，
由，即，解得 .
法二：函数图象可看作是由向左平移得到的，
则，即.
故选：D.
【一隅三反】
1．（2023秋·高一课时练习）函数（，且）的图象可能是（ ）
A． B．
C． D．
【答案】D
【解析】A，B选项中，，于是，所以图象与y轴的交点的纵坐标应在之间，
显然A，B的图象均不正确；
C，D选项中，，于是，图象与y轴的交点的纵坐标应在小于，所以D项符合.
故选：D
2．（2023·西藏林芝）的图像大致是（ ）
A．B．
C．D．
【答案】C
【解析】由题知，根据，，，
则，排除B，D，
当时，没有意义，排除A.
故选：C
3．（2023·全国·高三专题练习）（多选）对于函数且），，在同一直角坐标系下的图象可能为（ ）
A． B．
C． D．
【答案】AD
【解析】当a＞1时，f（x）＝ax是指数函数，单调递增，且图象过点（0，1），
而g（x）＝ax2﹣x＝a（x）2，对称轴x1，故A正确，B错误；
当0＜a＜1时，f（x）＝ax是指数函数，单调递减，且图象过点（0，1），
而g（x）＝ax2﹣x＝a（x）2，对称轴x，故D正确，C错误.
故选：AD．
4．（2023秋·宁夏石嘴山 ）函数，无论取何值，函数图像恒过一个定点，则定点坐标为 .
【答案】
【解析】则定点坐标为.
故答案为: .
5．（2023·全国·高一课堂例题）利用函数的图象，作出下列各函数的图象：
(1)；(2)；(3)；(4)；(5)．
【答案】作图见解析
【解析】（1）将图象向右平移一个单位即得，如下图，

（2）将右侧图象以y轴为对称轴作出左侧图象，去掉原图象左侧部分即得，如下图，

（3）将图象向下平移一个单位即得，如下图，

（4）以x轴为对称轴，画出与对称的图象即得，如下图，

（5）将（3）所得图象在x轴下方部分，翻折到上方即得，如下图，

考点五 指数函数型的单调性及应用
【例5-1】（2023秋·高一课时练习）函数的单调递增区间为（ ）
A．B．
C．D．
【答案】B
【解析】令，解得，
所以函数的定义域为，
因为开口向下，对称轴为，
可知在上单调递增，在上单调递减，
且在定义域内单调递增，
所以在上单调递增，在上单调递减，
又因为在定义域内单调递增，
所以在上单调递增，在上单调递减，
即函数的单调递增区间为.
故选：B.
【例5-2】（2023春·山东菏泽）设函数在区间单调递增，则a的取值范围是（ ）
A．B．
C．D．
【答案】A
【解析】函数在R上单调递增，而函数在区间上单调递增，
则有函数在区间上单调递增，因此，解得，
所以的取值范围是.
故选：A
【例5-3】（1）（2023·全国·高一专题练习）已知，，，则（ ）.
A．B．C．D．
（2）（2022秋·浙江宁波·高一校联考期中）下列大小关系正确的是（ ）
A．B．
C．D．
【答案】（1）B（2）A
【解析】（1），即；，即；
，即.所以有.故选：B.
（2）由幂函数在R上单调递增，则，
又指数函数在R上单调递减，则.则故选：A.
【例5-4】（2023·广东）已知函数，则不等式的解集为 ．
【答案】
【解析】构建函数，，可得函数单调递增，
，，则函数单调递增，
且，因此函数在上是增函数．
，，
解得，于是不等式的解集为．
故答案为：.
【一隅三反】
1．（2023秋·广东湛江）已知函数，则的增区间为（ ）
A．B．C．D．
【答案】A
【解析】函数定义域为，
令，又在上单调递增，的增区间为，
所以的增区间为.故选：A.
2．（2023春·宁夏石嘴山）设函数在区间上单调递增，则的取值范围为（ ）
A．B．C．D．
【答案】D
【解析】令，则二次函数的图象开口向上，对称轴为直线，
因为外层函数在上为减函数，函数在区间上为增函数，
所以，内层函数在上为减函数，故.故选：D.
3．（2022秋·青海海东·高一校考阶段练习）已知，则（ ）
A．B．C．D．
【答案】A
【解析】最小，
又，在上单调递增，
所以，即，
综上，，
故选：A．
4．（2022秋·江西南昌·高一统考期中）已知，则的大小关系为（ ）
A．B．
C．D．
【答案】B
【解析】，因为，所以，因此.
故选：B.
5（2023·河北）已知函数，则不等式的解集是（ ）
A．B．C．D．
【答案】A
【解析】因为，所以在上是奇函数.
因为在上是增函数，又在上是减函数，
所以在上是增函数.
所以，
所以，
所以不等式的解集是.
故选：
考点六 指数函数性质的综合运用
【例6-1】（2023春·河北石家庄·高一校考期末）已知函数为奇函数．
(1)求实数的值；
(2)求不等式的解集．
【答案】(1)
(2)
【解析】（1）（1）因为为奇函数，定义域为，
因为，即，
所以，经检验，符合题意．
（2）因为，
所以，
所以，
因为为奇函数，，
所以，
由（1）知：因为在R上递增，
所以在上是增函数，
所以，
解得，
所以不等式的解集是.
【例6-2】（2023秋·新疆塔城·高一乌苏市第一中学校考期末）已知函数奇函数．
(1)求a的值；
(2)判断在上的单调性并用定义证明；
(3)设，求在上的最小值．
【答案】(1)
(2)在上单调递增，证明见解析
(3)答案见解析
【解析】（1）解：是定义域为的奇函数，
；
经检验符合题意；
（2）在上单调递增．证明如下：
，
则，
因为，
所以，所以，，
可得．
即当时，有
所以在上单调递增．
（3）
，
令，又，则，
所以，，对称轴为，
则当时，；
当，；
当时，．
【一隅三反】
1．（2023秋·安徽）已知函数．
(1)若为奇函数，求的值；
(2)在（1）的条件下，求的值域．
【答案】(1)
(2)
【解析】（1）因为为奇函数，所以，
即，
所以.
（2）,
令，则 ，
因为，所以，
所以的值域．
2．（2023秋·河北衡水 ）已知函数（，且）是奇函数，且．
(1)求，的值；
(2)若对于，不等式成立，求的取值范围．
【答案】(1)，；
(2)
【解析】（1）因为函数是奇函数，所以，
即，得，
所以，，得或（舍），
综上，，；
（2）由（1）知，，
则恒成立，
，，
所以，对恒成立，
即恒成立，
设，函数由外层函数和内层函数复合而成，
当，，单调递增，当，单调递增，
所以根据复合函数的单调性可知，函数单调递增，最小值为，
即，则.
3．（2023秋·江苏南通 ）已知二次函数，且不等式的解集为.
(1)求解析式；
(2)若不等式在上有解，求实数的取值范围.
【答案】(1)
(2)
【解析】（1）由题意知的解集为，
故方程的两个根是1和3，
故，即，
故.
（2）由题意在上有解，即在上有解，
∵，∴在上的最大值，
设，则，则
又，当且仅当即时，等号成立，
∴，即实数的取值范围为.a＞1
0＜a＜1
图象
性质
定义域
R
值域
(0，＋∞)
过定点
过定点(0,1)，即x＝0时，y＝1
函数值的变化
当x＞0时，y＞1
当x＞0时，0＜y＜1
当x＜0时，0＜y＜1
当x＜0时，y＞1
单调性
在R上是增函数
在R上是减函数
对称性
y＝ax与y＝eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(1,a)))x的图象关于y轴对称