2024-2025学年上学期初中数学北师大版（2024）七年级期中必刷常考题之探索与表达规律

这是一份2024-2025学年上学期初中数学北师大版（2024）七年级期中必刷常考题之探索与表达规律，共21页。试卷主要包含了如图等内容，欢迎下载使用。

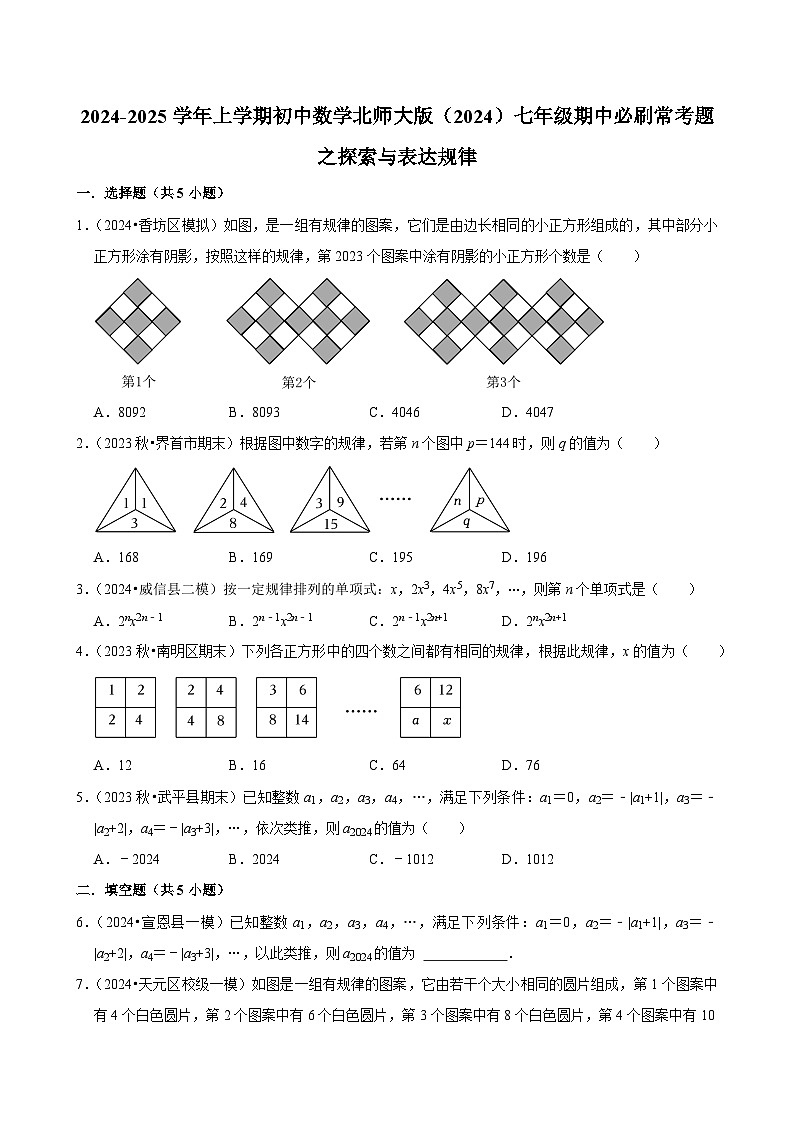
1．（2024•香坊区模拟）如图，是一组有规律的图案，它们是由边长相同的小正方形组成的，其中部分小正方形涂有阴影，按照这样的规律，第2023个图案中涂有阴影的小正方形个数是（ ）
A．8092B．8093C．4046D．4047
2．（2023秋•界首市期末）根据图中数字的规律，若第n个图中p＝144时，则q的值为（ ）
A．168B．169C．195D．196
3．（2024•威信县二模）按一定规律排列的单项式：x，2x3，4x5，8x7，⋯，则第n个单项式是（ ）
A．2nx2n﹣1B．2n﹣1x2n﹣1C．2n﹣1x2n+1D．2nx2n+1
4．（2023秋•南明区期末）下列各正方形中的四个数之间都有相同的规律，根据此规律，x的值为（ ）
A．12B．16C．64D．76
5．（2023秋•武平县期末）已知整数a1，a2，a3，a4，…，满足下列条件：a1＝0，a2＝﹣|a1+1|，a3＝﹣|a2+2|，a4＝﹣|a3+3|，…，依次类推，则a2024的值为（ ）
A．﹣2024B．2024C．﹣1012D．1012
二．填空题（共5小题）
6．（2024•宣恩县一模）已知整数a1，a2，a3，a4，…，满足下列条件：a1＝0，a2＝﹣|a1+1|，a3＝﹣|a2+2|，a4＝﹣|a3+3|，…，以此类推，则a2024的值为 ．
7．（2024•天元区校级一模）如图是一组有规律的图案，它由若干个大小相同的圆片组成，第1个图案中有4个白色圆片，第2个图案中有6个白色圆片，第3个图案中有8个白色圆片，第4个图案中有10个白色圆片，……依此规律，第2024个图案中应该有 个白色圆片．
8．（2024•岗巴县一模）如图：用棋子摆出下列一组“口”字，按照这种方法摆下去，则摆第n个“口”字需用棋子 个．
9．（2024春•聊城期中）如图，在∠AOB内部顺次有一组射线OP1，OP2，⋯，OPn，满足∠AOP1=12∠AOB，∠P1OP2=13∠P1OB，∠P2OP3=14∠P2OB，⋯，∠Pn−1OPn=1n+1∠Pn−1OB．若∠AOB＝α，则∠PnOB＝ ．（用含n，α的代数式表示）
10．（2024•垦利区模拟）如图，∠MON＝30˚，在OM上截取OA1=3．过点A1作A1B1⊥OM，交ON于点B1，以点B1为圆心，B1O为半径画弧，交OM于点A2；过点A2作A2B2⊥OM，交ON于点B2，以点B2为圆心，B2O为半径画弧，交OM于点A3；…按此规律，所得线段A2024B2024的长等于 ．
三．解答题（共5小题）
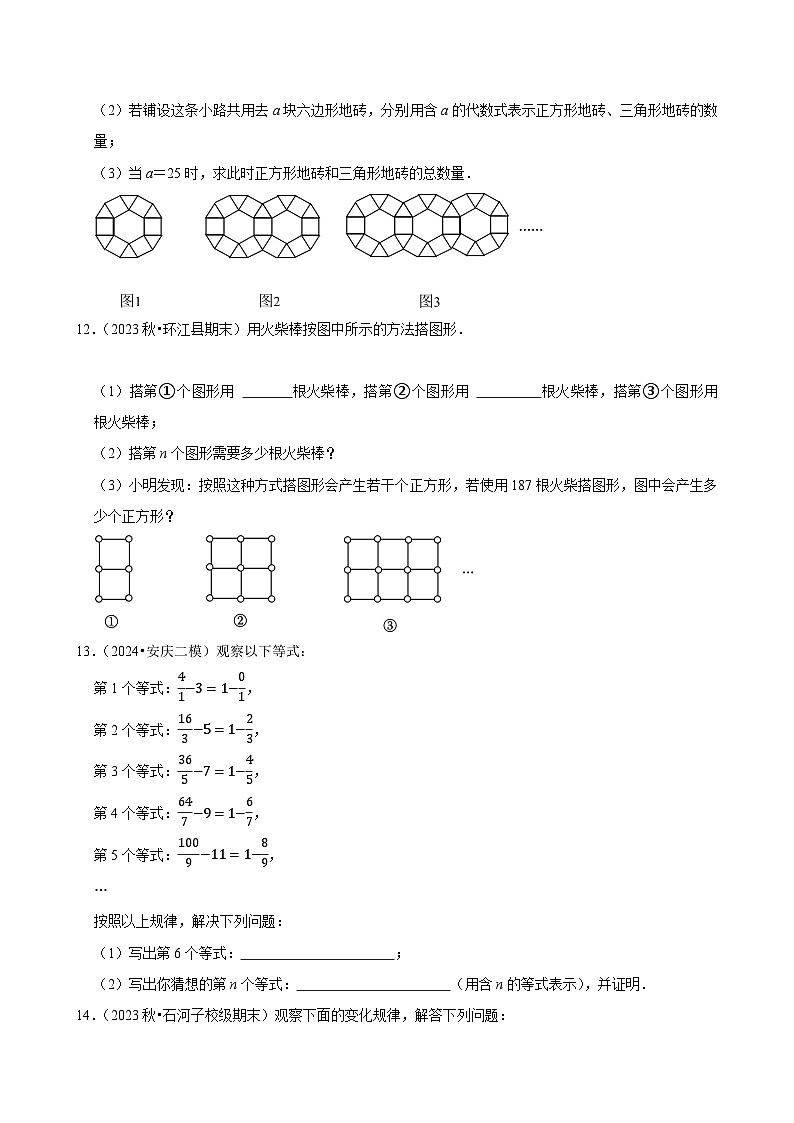
11．（2024•蜀山区模拟）某公园中的一条小路使用六边形、正方形、三角形三种地砖按照如图方式铺设．图1为有1块六边形地砖时，正方形地砖有6块，三角形地砖有6块；图2为有2块六边形地砖时，正方形地砖有11块，三角形地砖有10块；…．
（1）按照规律，每增加一块六边形地砖，正方形地砖会增加 块，三角形地砖会增加 块；
（2）若铺设这条小路共用去a块六边形地砖，分别用含a的代数式表示正方形地砖、三角形地砖的数量；
（3）当a＝25时，求此时正方形地砖和三角形地砖的总数量．
12．（2023秋•环江县期末）用火柴棒按图中所示的方法搭图形．
（1）搭第①个图形用 根火柴棒，搭第②个图形用 根火柴棒，搭第③个图形用 根火柴棒；
（2）搭第n个图形需要多少根火柴棒？
（3）小明发现：按照这种方式搭图形会产生若干个正方形，若使用187根火柴搭图形，图中会产生多少个正方形？
13．（2024•安庆二模）观察以下等式：
第1个等式：41−3=1−01，
第2个等式：163−5=1−23，
第3个等式：365−7=1−45，
第4个等式：647−9=1−67，
第5个等式：1009−11=1−89，
…
按照以上规律，解决下列问题：
（1）写出第6个等式： ；
（2）写出你猜想的第n个等式： （用含n的等式表示），并证明．
14．（2023秋•石河子校级期末）观察下面的变化规律，解答下列问题：
11×2=1−12，12×3=12−13，13×4=13−14，14×5=14−15．
（1）若n为正整数，猜想1n(n+1)= ；
（2）计算：12×3+13×4+14×5+⋯+1x(x+1)；（x为正整数）
（3）计算：11×3+13×5+15×7+17×9+19×11+111×13+113×15．
15．（2024春•鼓楼区期末）如图，把一些相同规格的碗整齐地叠放在水平桌面上，这摞碗的高度随着碗的数量变化而变化的情况如表格所示：
（1）h（cm）表示这摞碗的高度，x（只）表示这摞碗的数量，请用含x的代数式表示h；
（2）若这摞碗共有15个，求这摞碗的高度；
（3）若这摞碗的高度为11.2cm，求这摞碗的数量．
2024-2025学年上学期初中数学北师大版（2024）七年级期中必刷常考题之探索与表达规律
参考答案与试题解析
一．选择题（共5小题）
1．（2024•香坊区模拟）如图，是一组有规律的图案，它们是由边长相同的小正方形组成的，其中部分小正方形涂有阴影，按照这样的规律，第2023个图案中涂有阴影的小正方形个数是（ ）
A．8092B．8093C．4046D．4047
【考点】规律型：图形的变化类．
【专题】规律型；运算能力；推理能力．
【答案】B
【分析】先数出三个图形中阴影小正方形的个数，再总结规律并推广至一般情形，从而求出第2022个图案中涂有阴影的小正方形个数．
【解答】解：第一个图案有5个：5＝1×4+1，
第二个图案有9个：9＝2×4+1，
第三个图案有13个：13＝3×4+1，
…，
则第n个图形有：4⋅n+1＝（4n+1）个，
故第2023个图案中有4×2023+1＝8093（个）．
故选：B．
【点评】本题考查图案的变化规律问题，解决本题的关键是找到正确的变化规律即可．
2．（2023秋•界首市期末）根据图中数字的规律，若第n个图中p＝144时，则q的值为（ ）
A．168B．169C．195D．196
【考点】规律型：图形的变化类．
【专题】规律型；推理能力．
【答案】A
【分析】在“n”区域的规律是第n个图：n，在“P”区域的规律是第n个图：P＝n2，在“q”区域的规律是：第n个图：q＝（n+1）2﹣1；由p＝144，可求出n＝12，代入q的规律即可求解．
【解答】解：由图得：
在“n”区域的规律是：
第1个图：1，
第2个图：2，
第3个图：3，
……，
第n个图：n；
在“P”区域的规律是：
第1个图：1，
第2个图：22，
第3个图：32，
……，
第n个图：P＝n2；
在“q”区域的规律是：
第1个图：（1+1）2﹣1，
第2个图：（2+1）2﹣1，
第3个图：（3+1）2﹣1，
……，
第n个图：q＝（n+1）2﹣1；
当p＝144时，
n2＝144，
∴n＝12，
∴q＝（12+1）2﹣1＝168；
故选：A．
【点评】本题考查了数字类的规律探究，找出规律是解题的关键．
3．（2024•威信县二模）按一定规律排列的单项式：x，2x3，4x5，8x7，⋯，则第n个单项式是（ ）
A．2nx2n﹣1B．2n﹣1x2n﹣1C．2n﹣1x2n+1D．2nx2n+1
【考点】规律型：数字的变化类；单项式．
【专题】规律型；运算能力；推理能力．
【答案】B
【分析】根据题意得：第1个单项式为21﹣1x2×1﹣1，第2个单项式为2x3＝22﹣1x2×2﹣1，第3个单项式为4x5＝23﹣1x2×3﹣1，第4个单项式为8x7＝24﹣1x2×4﹣1，……，由此发现规律，即可求解．
【解答】解：根据题意得：第1个单项式为21﹣1x2×1﹣1，
第2个单项式为2x3＝22﹣1x2×2﹣1，
第3个单项式为4x5＝23﹣1x2×3﹣1，
第4个单项式为8x7＝24﹣1x2×4﹣1，
……，
由此得到第n个单项式为2n﹣1x2n﹣1．
故选：B．
【点评】本题主要考查了数字类规律题，明确题意，准确得到规律是解题的关键．
4．（2023秋•南明区期末）下列各正方形中的四个数之间都有相同的规律，根据此规律，x的值为（ ）
A．12B．16C．64D．76
【考点】规律型：数字的变化类．
【专题】猜想归纳；推理能力．
【答案】D
【分析】观察正方形表格中的四个数，发现变化规律即可解决问题．
【解答】解：观察题中所给表格可知，
左下角的数字：2＝21，4＝22，8＝23，…，
所以a＝26＝64．
右下角的数字：4＝2+2，8＝4+4，14＝6+8，…，
所以x＝a+12＝76．
故选：D．
【点评】本题考查数字变化的规律，能根据所给表格发现每个位置数的变化规律是解题的关键．
5．（2023秋•武平县期末）已知整数a1，a2，a3，a4，…，满足下列条件：a1＝0，a2＝﹣|a1+1|，a3＝﹣|a2+2|，a4＝﹣|a3+3|，…，依次类推，则a2024的值为（ ）
A．﹣2024B．2024C．﹣1012D．1012
【考点】规律型：数字的变化类．
【专题】猜想归纳；推理能力．
【答案】C
【分析】依次计算出a1，a2，a3，…，根据发现的规律即可解决问题．
【解答】解：由题知，
a1＝0，
a2＝﹣|a1+1|＝﹣1，
a3＝﹣|a2+2|＝﹣1，
a4＝﹣|a3+3|＝﹣2，
a5＝﹣|a4+4|＝﹣2，
a6＝﹣|a5+5|＝﹣3，
a7＝﹣|a6+6|＝﹣3，
…
由此可见，ai和ai+1（i为偶数）相等，且都等于−i2．
所以a2024=−20242=−1012．
故选：C．
【点评】本题考查实数计算中的规律问题，能根据所给的计算方式，求出前几个数并以此发现数的规律是解题的关键．
二．填空题（共5小题）
6．（2024•宣恩县一模）已知整数a1，a2，a3，a4，…，满足下列条件：a1＝0，a2＝﹣|a1+1|，a3＝﹣|a2+2|，a4＝﹣|a3+3|，…，以此类推，则a2024的值为 ﹣1012 ．
【考点】规律型：数字的变化类．
【专题】规律型；运算能力．
【答案】﹣1012．
【分析】根据题意，可以写出这列数的前几个数，从而可以发现数字的变化特点，从而可以得到a2024的值．
【解答】解：由题意可得，
a1＝0，
a2＝﹣|a1+1|＝﹣1，
a3＝﹣|a2+2|＝﹣1，
a4＝﹣|a3+3|＝﹣2，
a5＝﹣|a4+4|＝﹣2，
……，
∴a2023=−2023−12=−1011，
a2024＝﹣|﹣1011+2023|＝﹣1012．
故答案为：﹣1012．
【点评】本题考查数字的变化类，解答本题的关键是明确题意，发现数字的变化特点，写出相应项的值．
7．（2024•天元区校级一模）如图是一组有规律的图案，它由若干个大小相同的圆片组成，第1个图案中有4个白色圆片，第2个图案中有6个白色圆片，第3个图案中有8个白色圆片，第4个图案中有10个白色圆片，……依此规律，第2024个图案中应该有 4050 个白色圆片．
【考点】规律型：图形的变化类．
【专题】规律型；运算能力．
【答案】4050．
【分析】由于第1个图案中有4个白色圆片4＝2+2×1，第2个图案中有6个白色圆片6＝2+2×2，第3个图案中有8个白色圆片8＝2+2×3，第4个图案中有10个白色圆片10＝2+2×4，…，可得第n（n≥1）个图案中有白色圆片的总数为2+2n．从而可得答案．
【解答】解：第1个图案中有4个白色圆片4＝2+2×1，
第2个图案中有6个白色圆片6＝2+2×2，
第3个图案中有8个白色圆片8＝2+2×3，
第4个图案中有10个白色圆片10＝2+2×4，
…，
∴第n（n≥1）个图案中有（2+2n）个白色圆片．
∴第2024个图案中应该有2×2024+2＝4050个白色圆片．
故答案为：4050．
【点评】此题考查图形的变化规律，通过从一些特殊的数字变化中发现不变的因素或按规律变化的因素，然后推广到一般情况．解题关键是总结归纳出图形的变化规律．
8．（2024•岗巴县一模）如图：用棋子摆出下列一组“口”字，按照这种方法摆下去，则摆第n个“口”字需用棋子 4n 个．
【考点】规律型：图形的变化类．
【专题】规律型．
【答案】见试题解答内容
【分析】首先根据图形得到规律是：每增加一个数就增加四个棋子，然后根据规律解题即可．
【解答】解：
n＝1时，棋子个数为4＝1×4；
n＝2时，棋子个数为8＝2×4；
n＝3时，棋子个数为12＝3×4；
…；
n＝n时，棋子个数为n×4＝4n．
故答案为4n．
【点评】本题考查了图形的变化类问题，主要培养学生的观察能力和空间想象能力．
9．（2024春•聊城期中）如图，在∠AOB内部顺次有一组射线OP1，OP2，⋯，OPn，满足∠AOP1=12∠AOB，∠P1OP2=13∠P1OB，∠P2OP3=14∠P2OB，⋯，∠Pn−1OPn=1n+1∠Pn−1OB．若∠AOB＝α，则∠PnOB＝ αn+1 ．（用含n，α的代数式表示）
【考点】规律型：数字的变化类；列代数式．
【专题】规律型；运算能力．
【答案】αn+1．
【分析】根据∠AOB＝α，得出∠AOP1=12∠AOB=12α，求出∠P1OB=α−12α=12α，∠P2OB=12α−13×12α=13α，∠P3OB=13α−14×13α=14α，∠P4OB=14α−15×14α=15α，得出一般规律即可．
【解答】解：∵∠AOB＝α，
∴∠AOP1=12∠AOB=12α，
∴∠P1OB=α−12α=12α，
∴∠P1OP2=13∠P1OB=13×12α，
∴∠P2OB=12α−13×12α=13α，
∴∠P2OP3=14∠P2OB=14×13α，
∴∠P3OB=13α−14×13α=14α，
∴∠P3OP4=15∠P3OB=15×14α，
∴∠P4OB=14α−15×14α=15α，
⋯，
∴∠PnOB=αn+1．
故答案为：αn+1．
【点评】本题主要考查了图形规律探索，角的计算，解题的关键是根据已知条件，找出规律．
10．（2024•垦利区模拟）如图，∠MON＝30˚，在OM上截取OA1=3．过点A1作A1B1⊥OM，交ON于点B1，以点B1为圆心，B1O为半径画弧，交OM于点A2；过点A2作A2B2⊥OM，交ON于点B2，以点B2为圆心，B2O为半径画弧，交OM于点A3；…按此规律，所得线段A2024B2024的长等于 22023 ．
【考点】规律型：图形的变化类．
【专题】规律型；推理能力．
【答案】见试题解答内容
【分析】利用三角形中位线定理证明A2B2＝2A1B1，A3B3＝2A2B2＝22•A1B1，寻找规律解决问题即可．
【解答】解：∵B1O＝B1A2，B1A1⊥OA2，
∴OA1＝A1A2，
∵B2A2⊥OM，B1A1⊥OM，
∴B1A1∥B2A2，
∴B1A1=12A2B2，
∴A2B2＝2A1B1，
同法可得A3B3＝2A2B2＝22•A1B1，
…，
由此规律可得AnBn＝2n﹣1•A1B1，
∵∠MON＝30°，OA1=3，
∵A1B1＝1，
∴AnBn＝2n﹣1．
∴A2024B2024＝22023．
故答案为：22023．
【点评】本题考查规律型：图形的变化类，直角三角形的性质，三角形中位线定理，解题的关键是学会探究规律的方法，属于中考常考题型．
三．解答题（共5小题）
11．（2024•蜀山区模拟）某公园中的一条小路使用六边形、正方形、三角形三种地砖按照如图方式铺设．图1为有1块六边形地砖时，正方形地砖有6块，三角形地砖有6块；图2为有2块六边形地砖时，正方形地砖有11块，三角形地砖有10块；…．
（1）按照规律，每增加一块六边形地砖，正方形地砖会增加 5 块，三角形地砖会增加 4 块；
（2）若铺设这条小路共用去a块六边形地砖，分别用含a的代数式表示正方形地砖、三角形地砖的数量；
（3）当a＝25时，求此时正方形地砖和三角形地砖的总数量．
【考点】规律型：图形的变化类；列代数式；代数式求值．
【专题】猜想归纳；推理能力．
【答案】（1）5，4；
（2）用去正方形地砖的块数为（5a+1）块，用去三角形地砖的块数为（4a+2）块；
（3）此时正方形地砖和三角形地砖的总数量为228块．
【分析】（1）根据所给图形，依次求出图形中正方形和三角形地砖的块数，发现规律即可解决问题．
（2）根据（1）中发现的规律即可解决问题．
（3）根据（1）中发现的规律即可解决问题．
【解答】解：（1）由所给图形可知，
图1中三角形地砖块数为：6＝1×4+2，正方形地砖块数为：6＝1×5+1，六边形地砖块数为：1；
图2中三角形地砖块数为：10＝2×4+2，正方形地砖块数为：11＝2×5+1，六边形地砖块数为：2；
图3中三角形地砖块数为：14＝3×4+2，正方形地砖块数为：16＝3×5+1，六边形地砖块数为：3；
…，
所以图n中三角形地砖块数为（4n+2）块，正方形地砖块数为（5n+1）块，六边形地砖块数为n块；
由此可见，每增加一块六边形地砖，正方形地砖会增加5块，三角形地砖会增加4块．
故答案为：5，4．
（2）由（1）发现的规律可知，
当铺设这条小路共用去a块六边形地砖时，
用去正方形地砖的块数为（5a+1）块，用去三角形地砖的块数为（4a+2）块．
（3）当a＝25时，
5a+1＝5×25+1＝126（块），
4a+2＝4×25+2＝102（块），
所以126+102＝228（块），
即此时正方形地砖和三角形地砖的总数量为228块．
【点评】本题考查图形变化的规律，能根据所给图形发现三角形、正方形和六边形地砖块数变化的规律是解题的关键．
12．（2023秋•环江县期末）用火柴棒按图中所示的方法搭图形．
（1）搭第①个图形用 7 根火柴棒，搭第②个图形用 12 根火柴棒，搭第③个图形用 17 根火柴棒；
（2）搭第n个图形需要多少根火柴棒？
（3）小明发现：按照这种方式搭图形会产生若干个正方形，若使用187根火柴搭图形，图中会产生多少个正方形？
【考点】规律型：图形的变化类．
【专题】规律型；运算能力；推理能力．
【答案】（1）7，12，17；
（2）搭第n个图形需要（5n+2）根火柴棒；
（3）110个．
【分析】（1）直接观察图形即可得出答案；
（2）观察图形，归纳得出规律即可；
（3）观察图形得出：第n个图形共有3n﹣1个正方形，由5n+2＝187，求得n＝37，进而可求得相应的正方形个数．
【解答】解：（1）观察图形可得：搭第①个图形用火柴棒数为7，
搭第②个图形用火柴棒数为12，
搭第③个图形用火柴棒数为17，
故答案为：7，12，17；
（2）∵搭第①个图形用火柴棒数为7＝5×1+2，
搭第②个图形用火柴棒数为12＝5×2+2，
搭第③个图形用火柴棒数为17＝5×3+2，
……
∴搭第n个图形用火柴棒数为5n+2，
答：搭第n个图形需要（5n+2）根火柴棒；
（3）观察图形可得：第①个图形共有2个正方形，2＝3×1﹣1，
第②个图形共有5个正方形，5＝3×2﹣1，
第③个图形共有8个正方形，8＝3×3﹣1，
……
第n个图形共有3n﹣1个正方形，
∵5n+2＝187，
∴n＝37，
∴3n﹣1＝3×37﹣1＝110，
答：使用187根火柴搭图形，图中会产生110个正方形．
【点评】本题考查了规律型：图形的变化类，仔细观察图形得到后一个图形比前一个图形多5根火柴棒及后一个图形比前一个图形中正方形多3个是解题的关键．
13．（2024•安庆二模）观察以下等式：
第1个等式：41−3=1−01，
第2个等式：163−5=1−23，
第3个等式：365−7=1−45，
第4个等式：647−9=1−67，
第5个等式：1009−11=1−89，
…
按照以上规律，解决下列问题：
（1）写出第6个等式： 14411−13=1−1011 ；
（2）写出你猜想的第n个等式： 4n22n−1−(2n+1)=1−2n−22n−1 （用含n的等式表示），并证明．
【考点】规律型：数字的变化类；列代数式．
【专题】规律型；运算能力；推理能力．
【答案】（1）14411−13=1−1011；（2）4n22n−1−(2n+1)=1−2n−22n−1，证明见解析．
【分析】（1）观察等式中的4个数中的数字与等式的序号的关系，第一个数的分子是序号的2倍的平方，分母是从1开始的连续奇数，第二个数是从3开始的连续奇数，第三个数均是1，第四个数的分子是从0开始的连续偶数，分母是从1开始的连续奇数，以此规律可得结论；
（2）依据（1）中找出的规律得到第n个式子，通过计算式子的左边和右边来证明猜想的正确．
【解答】解：（1）观察等式中的4个数中的数字与等式的序号的关系可得：第一个数的分子是序号的2倍的平方，分母是从1开始的连续奇数，第二个数是从3开始的连续奇数，第三个数均是1，第四个数的分子是从0开始的连续偶数，分母是从1开始的连续奇数．
∴(2×6)22×6−1−(2×6+1)=1−2×(6−1)2×6−1．
即：14411−13=1−1011．
故答案为：14411−13=1−1011．
（2）依据（1）中找出的规律得到第n个式子为：
4n22n−1−(2n+1)=1−2n−22n−1．
证明：∵左边=4n2−(2n+1)(2n−1)2n−1=4n2−4n2+12n−1=12n−1，
右边=2n−1−(2n−2)2n−1=2n−1−2n+22n−1=12n−1，
∴左边＝右边．
∴等式成立．
故答案为：4n22n−1−(2n+1)=1−2n−22n−1．
【点评】本题主要考查了数字的变化的规律，列代数式，分式的加减．准确找出等式中的数字与等式序号的关系是解题的关键．
14．（2023秋•石河子校级期末）观察下面的变化规律，解答下列问题：
11×2=1−12，12×3=12−13，13×4=13−14，14×5=14−15．
（1）若n为正整数，猜想1n(n+1)= 1n−1n+1 ；
（2）计算：12×3+13×4+14×5+⋯+1x(x+1)；（x为正整数）
（3）计算：11×3+13×5+15×7+17×9+19×11+111×13+113×15．
【考点】规律型：数字的变化类．
【专题】规律型；运算能力．
【答案】（1）1n−1n+1；（2）x−12(x+1)；（3）715．
【分析】（1）猜想1n(n+1)=1n−1n+1，再根据异分母分式相加减计算，即可求解；
（2）根据（1）中的规律进行计算即可；
（3）根据（1）中的规律把原式变形为12×(1−13)+12×(13−15)+12×(15−17)+12×(17−19)+12×(19−111)+12×(111−113)+12×(113−115)，可得到12×(1−115)，即可求解．
【解答】解：（1）1n(n+1)=1n−1n+1；
验证：右边=1n−1n+1
=n+1n(n+1)−nn(n+1)
=n+1−nn(n+1)
=1n(n+1)
＝左边，
∴猜想成立；
故答案为：1n−1n+1；
（2）12×3+13×4+14×5+⋯+1x(x+1)
=12−13+13−14+14−15+⋅⋅⋅+1x−1x+1
=12−1x+1
=x+12(x+1)−22(x+1)
=x+1−22(x+1)
=x−12(x+1)；
（3）11×3+13×5+15×7+17×9+19×11+111×13+113×15
=12×(1−13)+12×(13−15)+12×(15−17)+12×(17−19)+12×(19−111)+12×(111−113)+12×(113−115)
=12×(1−13+13−15+15−17+17−19+19−111+111−113+113−115)
=12×(1−115)
=12×1415
=715．
【点评】本题主要考查了分式的加减运算，有理数加减运算．明确题意，准确得到规律是解题的关键．
15．（2024春•鼓楼区期末）如图，把一些相同规格的碗整齐地叠放在水平桌面上，这摞碗的高度随着碗的数量变化而变化的情况如表格所示：
（1）h（cm）表示这摞碗的高度，x（只）表示这摞碗的数量，请用含x的代数式表示h；
（2）若这摞碗共有15个，求这摞碗的高度；
（3）若这摞碗的高度为11.2cm，求这摞碗的数量．
【考点】规律型：图形的变化类；列代数式．
【专题】计算题；规律型；运算能力；推理能力．
【答案】（1）h＝1.2x+2.8；
（2）这摞碗的高度是20.8cm；
（3）碗的数量为7只．
【分析】（1）由表格中两个变量的变化关系可得：h＝4+1.2（x﹣1）＝1.2x+2.8；
（2）将x＝15代入h＝1.2x+2.8中计算即可；
（3）将h＝11.2cm代入h＝1.2x+2.8中计算即可．
【解答】解：（1）由表格中两个变量的变化关系可得：h＝4+1.2（x﹣1）＝1.2x+2.8，
答：用含x的代数式表示h为：h＝1.2x+2.8；
（2）当x＝15时，可得：h＝1.2×15+2.8＝20.8（cm），
答：当这摞碗共有15个时，这摞碗的高度是20.8cm；
（3）当h＝11.2cm时，将其代入h＝1.2x+2.8，
可列：1.2x+2.8＝11.2，
解得：x＝7，
答：当这摞碗的高度为11.2cm，碗的数量为7只．
【点评】本题考查的是图形的变化规律和列代数式，熟练掌握上述知识点是解题的关键．
考点卡片
1．列代数式
（1）定义：把问题中与数量有关的词语，用含有数字、字母和运算符号的式子表示出来，就是列代数式．
（2）列代数式五点注意：①仔细辨别词义． 列代数式时，要先认真审题，抓住关键词语，仔细辩析词义．如“除”与“除以”，“平方的差（或平方差）”与“差的平方”的词义区分． ②分清数量关系．要正确列代数式，只有分清数量之间的关系． ③注意运算顺序．列代数式时，一般应在语言叙述的数量关系中，先读的先写，不同级运算的语言，且又要体现出先低级运算，要把代数式中代表低级运算的这部分括起来．④规范书写格式．列代数时要按要求规范地书写．像数字与字母、字母与字母相乘可省略乘号不写，数与数相乘必须写乘号；除法可写成分数形式，带分数与字母相乘需把代分数化为假分数，书写单位名称什么时不加括号，什么时要加括号．注意代数式括号的适当运用． ⑤正确进行代换．列代数式时，有时需将题中的字母代入公式，这就要求正确进行代换．
【规律方法】列代数式应该注意的四个问题
1．在同一个式子或具体问题中，每一个字母只能代表一个量．
2．要注意书写的规范性．用字母表示数以后，在含有字母与数字的乘法中，通常将“×”简写作“•”或者省略不写．
3．在数和表示数的字母乘积中，一般把数写在字母的前面，这个数若是带分数要把它化成假分数．
4．含有字母的除法，一般不用“÷”（除号），而是写成分数的形式．
2．代数式求值
（1）代数式的值：用数值代替代数式里的字母，计算后所得的结果叫做代数式的值．
（2）代数式的求值：求代数式的值可以直接代入、计算．如果给出的代数式可以化简，要先化简再求值．
题型简单总结以下三种：
①已知条件不化简，所给代数式化简；
②已知条件化简，所给代数式不化简；
③已知条件和所给代数式都要化简．
3．规律型：数字的变化类
探究题是近几年中考命题的亮点，尤其是与数列有关的命题更是层出不穷，形式多样，它要求在已有知识的基础上去探究，观察思考发现规律．
（1）探寻数列规律：认真观察、仔细思考，善用联想是解决这类问题的方法，通常将数字与序号建立数量关系或者与前后数字进行简单运算，从而得出通项公式．
（2）利用方程解决问题．当问题中有多个未知数时，可先设出其中一个为x，再利用它们之间的关系，设出其他未知数，然后列方程．
4．规律型：图形的变化类
图形的变化类的规律题
首先应找出图形哪些部分发生了变化，是按照什么规律变化的，通过分析找到各部分的变化规律后直接利用规律求解．探寻规律要认真观察、仔细思考，善用联想来解决这类问题．
5．单项式
（1）单项式的定义：数或字母的积组成的式子叫做单项式，单独的一个数或字母也是单项式．
用字母表示的数，同一个字母在不同的式子中可以有不同的含义，相同的字母在同一个式子中表示相同的含义．
（2）单项式的系数、次数
单项式中的数字因数叫做单项式的系数，一个单项式中所有字母的指数的和叫做单项式的次数．
在判别单项式的系数时，要注意包括数字前面的符号，而形如a或﹣a这样的式子的系数是1或﹣1，不能误以为没有系数，一个单项式的次数是几，通常称这个单项式为几次单项式．碗的数量（只）
1
2
3
4
5
…
高度（cm）
4
5.2
6.4
7.6
8.8
…
碗的数量（只）
1
2
3
4
5
…
高度（cm）
4
5.2
6.4
7.6
8.8
…