

宁夏回族自治区吴忠市2023-2024学年八年级下学期期中数学试卷(解析版)
展开一、选择题
1. 若式子在实数范围内有意义,则的取值范围是( )
A. B. C. D.
【答案】B
【解析】由题意知:被开方数,
解得:,
故选:B.
2. 的倒数为( )
A. B. 2C. D.
【答案】C
【解析】∵,
∴的倒数是.
故选:C.
3. 若,则的值为 ( )
A. 2B. C. D.
【答案】A
【解析】∵,
∴,
∴,
故选A
4. 在直角坐标系中,点到原点的距离是( )
A. B. C. D. 2
【答案】B
【解析】如图所示:过点P作轴于点A,
则,,
∴
故选:B.
5. 在中,斜边,则等于( )
A. 8B. 4C. 6D. 以上都不对
【答案】A
【解析】∵在中,斜边为,
∴,
∵,
∴,
∴,
故选A.
6. 如图,在▱ABCD中,已知AD=5cm,AB=3cm,AE平分∠BAD交BC边于点E,则EC等于 ( )
A. 1cmB. 2cmC. 3cmD. 4cm
【答案】B
【解析】如图,
∵AE平分∠BAD交BC边于点E,
∴∠BAE=∠EAD,
∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC=5cm,
∴∠DAE=∠AEB,
∴∠BAE=∠AEB,
∴AB=BE=3cm,
∴EC=BC-BE=5-3=2cm.
故选B.
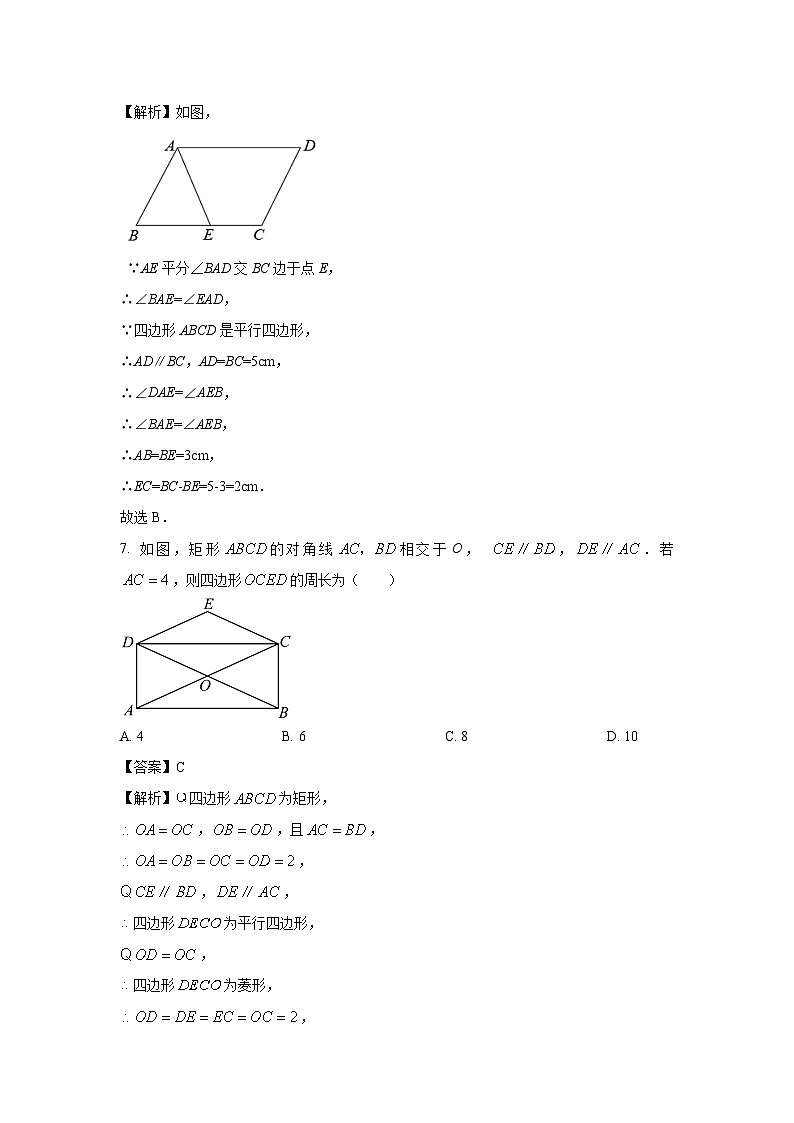
7. 如图,矩形的对角线相交于O, ,.若,则四边形的周长为( )
A. 4B. 6C. 8D. 10
【答案】C
【解析】四边形为矩形,
,,且,
,
,,
四边形为平行四边形,
,
四边形为菱形,
,
则四边形的周长为,
故选:C.
8. 已知四边形是平行四边形,下列结论中不一定成立的是 ( )
A. B.
C. 当时,它是菱形D. 当时,它是矩形
【答案】B
【解析】A.∵四边形是平行四边形,
∴正确,故A不符合题意.
B.∵四边形是平行四边形,
∴不一定相等,故B符合题意.
C.∵四边形是平行四边形,
∴当时,它是菱形,故C不符合题意.
D.∵四边形是平行四边形,
∴当时,它是矩形,故D不符合题意.
故选:B.
9. 矩形两条对角线夹角为,对角线长,则矩形较短的边长为( )
A. B. C. D.
【答案】D
【解析】如图,由题意可知,,
∵在矩形中,
∴,
又∵,
∴是等边三角形,
∴,
∴矩形较短边长为,
故选:D.
10. 如图,在菱形ABCD中,∠A=60°,AD=4,点P是AB边上的一个动点,点E、F分别是DP、BP的中点,则线段EF的长为( )
A. 2B. 4C. D.
【答案】A
【解析】连接BD,
因为,四边形ABCD是菱形,
所以,AB=AD=4,
又因为∠A=60°,
所以,三角形ABD是等边三角形.
所以,BD=AB=AD=4
因为,E,F是DP、BP的中点,
所以,EF是三角形ABD的中位线,
所以,EF=BD=2
故选A
二、填空题
11. 若最简二次根式与可以合并,则__________.
【答案】2
【解析】∵最简二次根式与可以合并,
∴最简二次根式与是同类二次根式,
∴,
∴,
故答案为:2.
12. 计算:的结果为___.
【答案】1
【解析】
.
故答案为:1.
13. 计算: _____________.
【答案】
【解析】
故答案为:.
14 若实数a、b满足,则代数式= _____________.
【答案】
【解析】∵
∴,
∴,
∴.
故答案为.
15. 在实数范围内分解因式:a3-7a=________.
【答案】
【解析】,
故答案为:.
16. 如图,有一长、宽各2m、高3m且封闭的长方体纸盒,一只昆虫从顶点A爬到与A点相对的顶点B,那么这只昆虫爬行的最短路径为__________m.
【答案】
【解析】由题意得,路径一:
;
路径二:
;
路径三:
;
,
为最短路径.
故答案为:
17. 如图,在正方形的外侧,作等边,则____.
【答案】
【解析】∵四边形是正方形,
∴,,
∵是等边三角形,,
∴,,
∴,,
∴,
故答案为:.
18. 如图,若面积为12,则阴影面积为__________
【答案】3
【解析】如图,
∵四边形是平行四边形,
∴,,,
∴,,,
∴,
∴,
∴阴影部分的面积等于.
故答案为:3
19. 如图,在中,于点E,于点F,若,则_____
【答案】
【解析】,,
,
∵,
,
∵四边形是平行四边形,
,
,
.
故答案为:.
20. 用直角边分别为3和4的两个直角三角形拼成一个平行四边形(非矩形),所得的平行四边形的周长是______.
【答案】18或16
【解析】直角边分别为3和4,
斜边为:,
若以边长为3的边为对角线,则所得的平行四边形的周长是:;
若以边长为4的边为对角线,则所得的平行四边形的周长是:;
若以边长为5的边为对角线,则所得的平行四边形的周长是:(此时是矩形,舍去);
综上可得:所得的平行四边形的周长是:16或18.
故答案为:16或18.
三、解答或证明题
21. 计算:
(1);
(2).
解:(1)
(2)
.
22. 先化简,再求值:,其中
解:原式=
=
当时,原式=.
23. 如图,在中,,BC边上的中线.求证:是等腰三角形.
证明:,为的中线,
,
,,,
,
为直角三角形,
,
,
,
,
是等腰三角形.
24. 如图,O是对角线的中点,过点O的直线分别与、交于点E、F.证明:四边形是平行四边形.
证明:∵点O为对角线的中点,
∴,,
∴,,
∴,
∴,
又,
∴四边形是平行四边形.
25. 如图,菱形花坛的边长为,,沿着菱形的对角线修建了两条小路和,求两条小路的长和花坛的面积.
解:∵花坛是菱形,
,
中,
,
.
∵,
∴菱形花坛的面积是.
26. 如图,矩形ABCD中,AB=8,BC=4,将矩形沿对角线AC折叠,点D落在D′处.
(1)求证:AF=CF
(2)求重叠部分△AFC的面积.
(1)证明:依题意可知,矩形沿对角线AC对折后有:
∠D′=∠B=90°,∠AFD′=∠CFB,BC=AD′
∴△AD′F≌△CBF(AAS)
∴CF=AF
(2)解:设AF=CF=x
∴BF=8﹣x
在Rt△BCF中有BC2+BF2=FC2
即42+(8﹣x)2=x2
解得x=5.
∴S△AFC=AF•BC=×5×4=10.
27. 如图所示,在四边形ABCD中,AD∥BC,AD=24cm,BC=30cm,点P从A向点D以1cm/s的速度运动,到点D即停止.点Q从点C向点B以2cm/s的速度运动,到点B即停止.直线PQ将四边形ABCD截得两个四边形,分别为四边形ABQP和四边形PQCD,则当P,Q两点同时出发,几秒后所截得两个四边形中,其中一个四边形为平行四边形?
解:设当P,Q两点同时出发,t秒后,四边形ABQP或四边形PQCD是平行四边形,
根据题意可得:
AP=tcm,PD=(24-t)cm,CQ=2tcm,BQ=(30-2t)cm,
①若四边形ABQP是平行四边形, 则AP=BQ,
∴t=30-2t, 解得:t=10,
∴10s后四边形ABQP是平行四边形;
②若四边形PQCD是平行四边形, 则PD=CQ,
∴24-t=2t, 解得:t=8,
∴8s后四边形PQCD是平行四边形;
综上:当P,Q两点同时出发,8秒或10秒后,四边形ABQP或四边形PQCD是平行四边形.
宁夏回族自治区吴忠市第六中学2023-2024学年八年级下学期期中质量检测数学试卷: 这是一份宁夏回族自治区吴忠市第六中学2023-2024学年八年级下学期期中质量检测数学试卷,共4页。
[数学]宁夏回族自治区吴忠市2023-2024学年八年级下学期期中试题(解析版): 这是一份[数学]宁夏回族自治区吴忠市2023-2024学年八年级下学期期中试题(解析版),共14页。试卷主要包含了选择题,填空题,解答或证明题等内容,欢迎下载使用。
宁夏回族自治区吴忠市青铜峡市2023-2024学年九年级下学期期中数学试题(原卷版+解析版): 这是一份宁夏回族自治区吴忠市青铜峡市2023-2024学年九年级下学期期中数学试题(原卷版+解析版),文件包含宁夏回族自治区吴忠市青铜峡市2023-2024学年九年级下学期期中数学试题原卷版docx、宁夏回族自治区吴忠市青铜峡市2023-2024学年九年级下学期期中数学试题解析版docx等2份试卷配套教学资源,其中试卷共30页, 欢迎下载使用。












