湖北省宜昌市长阳县2024年中考模拟数学试卷(解析版)

这是一份湖北省宜昌市长阳县2024年中考模拟数学试卷(解析版)，共20页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
1. 2024的倒数是（ ）
A. B. C. 2024D.
【答案】A
【解析】 ， 2024的倒数是．
故选：A．
2. 下列图案，既是轴对称图形又是中心对称图形的是（ ）
A. B.
C. D.
【答案】C
【解析】A．不是轴对称图形，是中心对称图形，故不符合题意；
B．是轴对称图形，不是中心对称图形，故不符合题意；
C．是轴对称图形，也是中心对称图形，故不符合题意；
D．不是轴对称图形，是中心对称图形，故不符合题意；
故选：C．
3. 下列运算正确的是（ ）
A. B.
C. D.
【答案】D
【解析】A．，故选项错误，不符合题意；
B．，故选项错误，不符合题意；
C．，故选项错误，不符合题意；
D．，故选项正确，符合题意．
故选：D．
4. 不等式的解集在数轴上表示为（ ）
A. B.
C. D.
【答案】A
【解析】
∴，
∴，
∴，
在数轴上表示为：
故选：A．
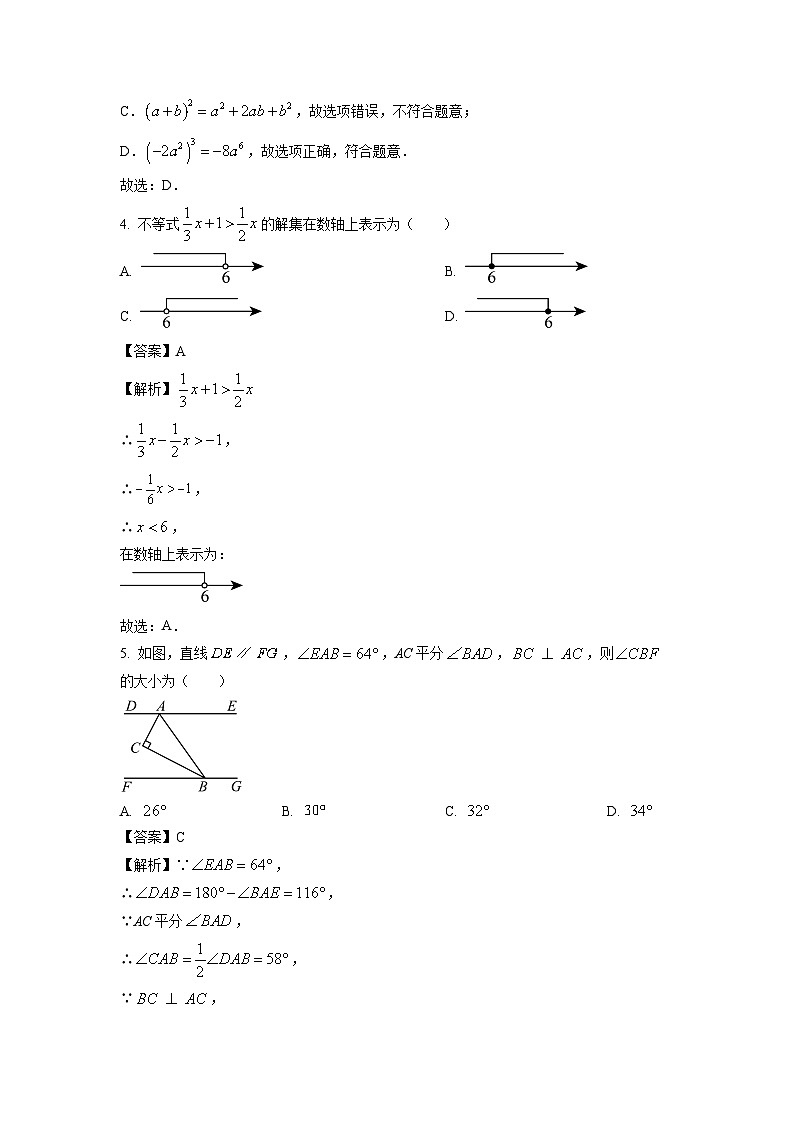
5. 如图，直线，，AC平分，，则的大小为（ ）
A. B. C. D.
【答案】C
【解析】∵，
∴，
∵AC平分，
∴，
∵，
∴，
∵，
∴，
∴，
故选C．
6. 已知正n边形的内角和是它的外角和的3倍，则这个正n边形的中心角为（ ）
A. B. C. D.
【答案】D
【解析】根据题意，得，
解得，
∴这个正n边形的中心角为，
故选：D．
7. 下列说法正确的是（ ）
A. 旅客乘坐飞机，需进行安全检查，安检宜采用抽样调查的方式
B. 五位同学某次考试的成绩分别为76分、72分、94分、101分、65分，则这组数据的中位数为94分
C. 甲、乙两位同学同时进行了5轮篮球训练，每轮训练各投篮10次，两人进球个数平均数都为6，甲的成绩的方差为6.4，乙的成绩的方差为14.6，则乙的成绩更稳定
D. 一组数据1，4，5，a，b，其中a，b是一元二次方程的两根，则这组数据的平均数为3
【答案】D
【解析】A. 旅客乘坐飞机，需进行安全检查，安检宜采用全面调查的方式，故该选项错误，不合题意；
B. 五位同学某次考试的成绩分别为76分、72分、94分、101分、65分，
按从小到大排序为：65分、72分、76分、94分、101分，
则这组数据的中位数为76分，故该选项错误，不合题意；
C. 甲、乙两位同学同时进行了5轮篮球训练，每轮训练各投篮10次，两人进球个数平均数都为6，甲的成绩的方差为6.4，乙的成绩的方差为14.6，则甲的成绩更稳定，故该选项错误，不合题意；
D. 一组数据1，4，5，a，b，其中a，b是一元二次方程的两根，
∵解得，
∴这组数据为1，4，5，2，3，
则这组数据的平均数为，故该选项正确，符合题意；
故选：D．
8. 如图，与相切于点A，的延长线交于点C，连接，已知，则的大小为（ ）
A. B. C. D.
【答案】C
【解析】如图所示，连接，
∵是的切线，
∴，
∴，
∵，
∴，
∴，
∵，
∴，
解得：，
∴，
故选：C．
9. 如图，在中，，，对角线，相交于点O，经过点O的直线分别交，于点M，N，当恰好平分时，的长为（ ）
A. 2B. 3C. 4D. 6
【答案】B
【解析】∵平分，
∴，
∴四边形是平行四边形，
∴，，
∴，
∴，，
∴，
∵，，，
∴，
∴，
∴，
故选：B．
10. 如图，已知二次函数的图象关于直线对称，与x轴的一个交点在原点和之间，下列结论错误的是（ ）
A. B.
C. D. （m任意实数）
【答案】C
【解析】A．∵抛物线开口向上，
∴，
∵对称轴为直线，
∴，
∴，
∵抛物线与轴交于负半轴，
∴，
∴，
原题结论正确，故此选项不符合题意；
B．∵对称轴为直线，
∴，
∴，
故选项正确，不符合题意；
C．∵对称轴为直线，，
∴，
∴当时，
原题结论错误，故此选项符合题意；
D．当时，为最小值，
∴，∴，∴，
原题结论正确，故此选项不符合题意．
故选：C．
二、填空题（共5题，每题3分，共15分）
11. 计算：________．
【答案】2
【解析】原式
．
12. 如图所示的是一个电路图，当随机闭合开关，，中的两个时，小灯泡发光的概率为________．
【答案】
【解析】画树状图得：
∵共有6种等可能的结果，能够让灯泡发光的是闭合， ，，，
∴能够让灯泡发光的概率为．
故答案为：．
13. 《九章算术》是中国古代重要的数学著作，其中“盈不足术”记载：今有共买鸡，人出九，盈十一；人出六，不足十六．问人数鸡价各几何？译文：今有人合伙买鸡，每人出9钱，会多出11钱；每人出6钱，又差16钱．问人数、买鸡的钱数各是多少．答：人数为________人，买鸡的钱数为________钱．
【答案】9 70
【解析】设人数为x，买鸡的钱数为y，
根据题意，得，解得，
故答案为：9，70．
14. 如图，矩形的边在x轴的负半轴上，对角线的延长线与y轴交于点E，反比例函数的图象经过点A，当的面积为6时，k的值为________．
【答案】
【解析】设，，
∴，
∵四边形为矩形，
∴，
∵，
∴，
∴，
∴，
∴，
∵，
∴，
∵反比例函数的图象经过点A，
∴，
故答案为：．
15. 如图，在中，，，D是上一点，，点M在上，点N在上，将沿折叠，点A恰好与点D重合，则折痕的长为________．
【答案】
【解析】过M作于G，过N作于H，
∵，，
∴，，
∵，
∴，，
设，，
∵，，，
∴，是等腰直角三角形，
∴，，
∴，
∵将沿折叠，点A恰好与点D重合，
∴，，，
∴，
又，
∴，
∴，即，
整理得，
解得或（舍去）
∴
∴
故答案为：．
三、解答题（共9题，共75分，解答应写出文字说明、证明过程或演算步骤）
16. 计算：．
解：.
17. 如图，在中，，B是的中点，于点G，过F作的平行线交的延长线于点C，延长至点D，使，连接，判断四边形的形状，并说明理由．
解：四边形是菱形
理由：∵，B是的中点，
∴，
∵，，
∴，
∴，
∴，
∵，
∴，
又，
∴四边形是平行四边形，
又
∴平行四边形是菱形．
18. “恒升包装”公司的产品质量上乘，信誉良好．该公司今年3月初接到商家24000件产品的订单，按计划生产5天后，商家因需求将产品追加5000件，该公司经理加大对工人的奖励力度，提高工人的积极性，结果每天比原计划多生产200件，刚好（包括前面5天一起）在原计划的时间内完成生产任务按时交付商家．该公司原计划每天生产产品多少件？
解：设原计划每天生产产品x件，
根据题意，得，
解得，
经检验是原方程的解，
答：原计划每天生产产品800件．
19. 为提高广大市民的消防安全意识，和平社区大力进行“远离火灾，珍爱生命，共建平安家园”宣传活动，为了了解本次活动的效果，社区抽取部分市民进行了调查，根据调查结果绘制了如图所示两幅不完整的统计图，其中A：“不了解”，B：“了解一些”，C：“基本了解”，D：“非常了解”．
（1）本次共调查了 人，D组所在扇形的圆心角的大小是 °；
（2）补全条形统计图；
（3）若该社区共5000人，估计该社区对消防知识“不了解”的人数；
（4）“安全无小事”，根据这次调查结果，说说你的看法或对该社区工作的建议．
解：（1），
∴本次共调查了200人，
∴D组的人数为人，
∴D组所在扇形的圆心角的大小是，
故答案为：200，72；
（2）补图如下：
（3），
∴对消防知识“不了解”的人数为500人；
（4）利用社区文化活动，体育活动，进行安全知识竞赛宣传，特别要各多组织一些“以人为本，安全第一”为主题的社区活动．如：“安全生产进社区”活动、“安全生产进家庭”活动等等．
20. 如图，已知反比例函数与一次函数的图象交于点A和点．
（1） ， ；
（2）C是线段延长线上一点，轴，垂足为E，交反比例函数的图象于点D，若的面积为18，求点C的坐标．
解：（1）把分别代入、，
得，，
解得，，
故答案为：6，；
（2）由（1）知：、
设，
∵轴，
∴C、D的纵坐标相同，
∴D的纵坐标为，
∴D的横坐标为，
∵的面积为18，
∴，
解得，（舍去），
∴．
21. 如图，四边形是平行四边形，过A，C，D三点的与相切于点A，与交于点E，连接，．
（1）求证：；
（2）若，，求的长．
（1）证明：过A作直径，连接，，
∴，
∴，
∵是切线，
∴，即，
∴，
∵，
∴，
∵四边形是平行四边形，
∴，，
∴，
∴，
∴，
∵，，，
∴，
∴，
又，，
∴；
（2）解：∵，
∴，
∵，，
∴，
又，
∴，，
∴，，
∴，
∴，
∴，
∴．
22. 麻花是我国的一种特色油炸面食小吃，色、香、味俱全，品种多样，十分畅销．阳光超市购进了一批麻花礼盒进行销售，成本价为30元/件，根据市场预测，在一段时间内，销售单价为40元/件时，每天的销售量为300件，销售单价每提高10元/件，将少售出50件．
（1）求超市销售该麻花礼盒每天的销售量y（件）与销售单价x（元/件）之间的函数关系式；
（2）当销售单价定为多少时，超市销售该麻花礼盒每天获得的利润最大？并求出最大利润；
（3）若超市销售该麻花礼盒每天要获得不低于5000元的利润，但物价部门规定，销售该麻花礼盒的利润率不得高于，该超市应如何确定销售单价．
解：（1）；
（2）设利润为w元，由题意得
，
∴当时，w最大为6125，
∴当销售单价定为65元时，超市销售该麻花礼盒每天获得的利润最大，最大利润为6125元；
（3）由题意得，，解得，
所以，销售单价应为元．
23. 【实践操作】
（1）如图1，是等边三角形，D是外一点，且，如果将绕点A顺时针旋转，得到，直接写出线段，，之间的数量关系；
【类比探究】
（2）如图2，是等腰直角三角形，，D是外一点，且，试写出线段，，之间的数量关系，并说明理由；
【拓展应用】
（3）如图3，在四边形中，，，若，，，求的长和四边形的面积．
解：[实践操作]
理由：∵是等边三角形，
∴，，
∵，
∴，
∵绕点A顺时针旋转，得到，
∴，，
∴，，，
∴是等边三角形，
∴，E、B、D三点共线，
又，
∴；
[类比探究]
理由：∵是等腰直角三角形，∴，，
∵，∴，
将绕点A顺时针旋转，得到，
∴，，
∴，，，
∴等腰直角三角形，E、B、D三点共线，
∴，
又，∴；
[拓展应用]
过A作于E，于F，连接，
∵，
设，则，
∴，
∴，
∴，
∴，，
∴，
∵，
∴，
又，
∴，
又，，
∴，
∴，，
又，
∴，
∴，
∴，
∴
．
24. 已知直线与x轴交于点B，与y轴交于点C，抛物线经过B，C两点，与x轴的另一个交点为A，其顶点为D，P是抛物线上的动点．
（1）求抛物线的解析式，并写出D点坐标；
（2）如图1，点在抛物线上，连接，点P在抛物线对称轴左侧，满足，请求出点P的坐标；
（3）如图2，连接，．
①判断的形状；
②当时，直接写出点P的坐标．
解：（1）当时，，
∴，
当时，，解得，
∴，
把B、C的坐标代入，得，
解得，
∴，
∴顶点D的坐标为；
（2）把代入，得，
∴，
∴轴，则轴，，
∵，，
∴，
如图，连接，过B作于F，
则四边形是矩形，
又，
∴四边形是正方形，
∴，，
∴，
∵，
∴，
又，
∴，
∴，
∴，
设的解析式为，
则，
解得，
∴，
联立方程组，
解得或，
∴
（3）①∵，，，
∴，，，
∴，∴是直角三角形，其中；
②当在的上方时，如图，
设直线解析式为，
则，解得，
∴，
∵，
∴，
∴设的解析式为，
∴，
∴，
联立方程组，
解得或，
∴P的坐标为；
当在的下方时，
如图，过B作，交于G，过G作于H
又①知，
∴，
又，，
∴，
∴，
∵，，
∴，
∴，
∴，
∴，
又，
∴，
∴，
∴设的解析式为，
∴，
∴，
∴
联立方程组，
解得或，
∴P坐标为；
综上，P的坐标为或．