数学必修 第一册2.1 等式性质与不等式性质综合训练题

这是一份数学必修 第一册2.1 等式性质与不等式性质综合训练题，共30页。
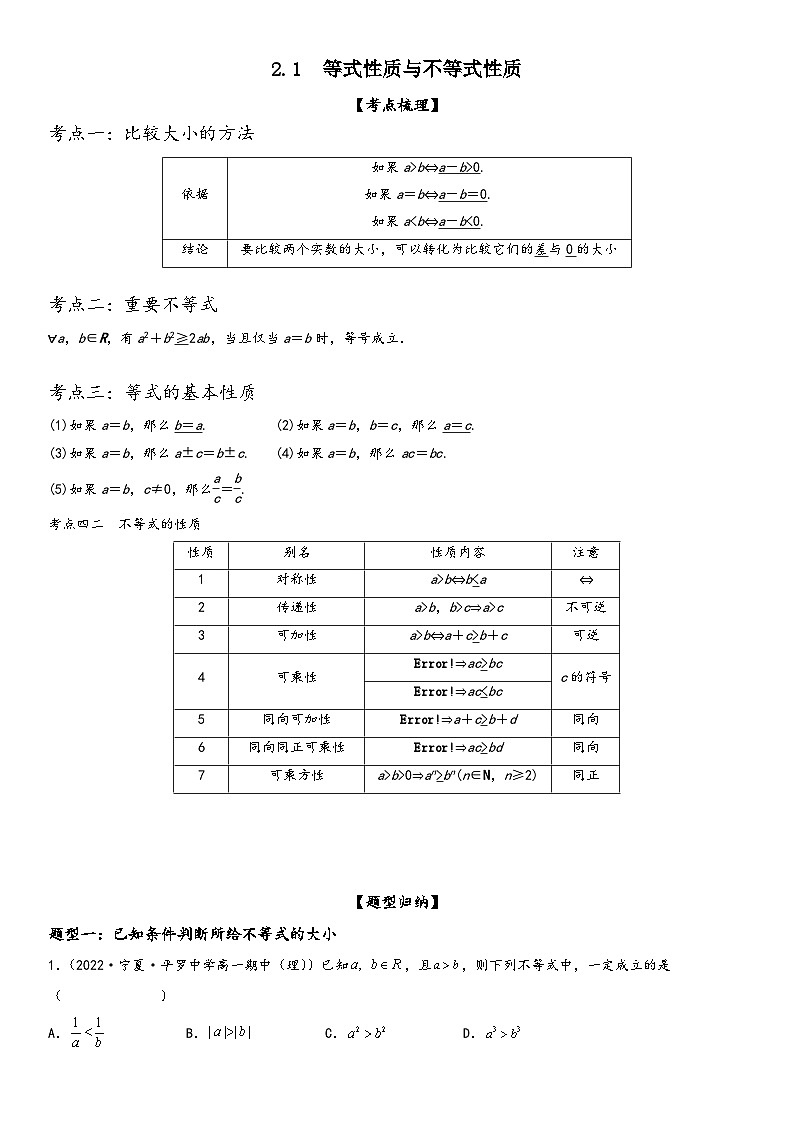
考点一：比较大小的方法
考点二：重要不等式
∀a，b∈R，有a2＋b2≥2ab，当且仅当a＝b时，等号成立．
考点三：等式的基本性质
(1)如果a＝b，那么b＝a.(2)如果a＝b，b＝c，那么a＝c.
(3)如果a＝b，那么a±c＝b±c.(4)如果a＝b，那么ac＝bc.
(5)如果a＝b，c≠0，那么eq \f(a,c)＝eq \f(b,c).
考点四二 不等式的性质
【题型归纳】
题型一：已知条件判断所给不等式的大小
1．（2022·宁夏·平罗中学高一期中（理））已知，且，则下列不等式中，一定成立的是（ ）
A．B．C．D．
2．（2022·内蒙古·赤峰市元宝山区第一中学高一期中）若，则下列不等式不能成立的是（ ）
A．B．C．D．
3．（2022·四川省峨眉第二中学校高一期中（理））若，则下列不等式正确的是（ ）
A．B．C．D．
题型二：不等式的性质比较数的大小
4．（2022·浙江省淳安中学高一期中）已知实数满足，则“”是“”（ ）
A．充分不必要条件B．必要不充分条件
C．充分必要条件D．既不充分也不必要条件
5．（2022·重庆巴蜀中学高一期末）若，则下列不等式一定成立的是（ ）
A．B．C．D．
6．（2022·山东青岛·高一期末）已知，则下述一定正确的是（ ）
A．B．
C．D．
题型三：作差法或作商法比较不等式的大小
7．（2022·甘肃张掖·高一期末）若，，则下列结论正确的是（ ）
A．B．C．D．a，b大小不确定
8．（2021·山东·泰安一中高一期中）设，，则（ ）．
A．B．C．D．
9．（2022·河北沧州·高一期末）下列说法正确的是（ ）
A．若，，则B．若a，，则
C．若，，则D．若，则
题型四：利用不等式求取值范围
10．（2022·吉林延边·高一期末）已知，，则的取值范围是（ ）
A．B．
C．D．
11．（2022·江苏·高一）已知，则的取值范围为（ ）
A．B．C．D．
12．（2021·全国·高一专题练习）下列选项中，使不等式成立的x的取值范围是（ ）
A．B．
C．D．
题型五：由不等式性质证明不等式
13．（2022·湖南·高一课时练习）利用不等式的性质证明下列不等式：
(1)若，，则；
(2)若，，则．
14．（2022·湖南·高一课时练习）求证：
(1)若，且，则；
(2)若，且，同号，，则；
(3)若，且，则．
15．（2021·湖南·衡阳市田家炳实验中学高一阶段练习）（1）已知a，b，c，d均为正数.求证：
（2）已知.求证：y
【双基达标】
一、单选题
16．（2022·内蒙古·赤峰二中高一阶段练习（理））下列命题正确的是（ ）
A．若，则B．若，则
C．若，则D．若，则
17．（2022·江苏·高一）已知，，，则的大小关系为（ ）
A．B．C．D．无法确定
18．（2022·湖南·新化县教育科学研究所高一期末）已知a，b，c，d均为实数，则下列命题正确的是（ ）
A．若，，则B．若，，则
C．若，则D．若，则
19．（2022·广东珠海·高一期末）对于任意实数，给定下列命题正确的是（ ）
A．若，则B．若，则
C．若，则D．若，则
20．（2022·湖南·高一课时练习）已知00，求证：
50．（2021·全国·高一）已知，，，求证：
(1)；
(2).
（2021·全国·高一）
（1）若bc－ad≥0，bd>0，求证：≤；
（2）已知c>a>b>0，求证：；
（3）观察以下运算：
1×5＋3×6>1×6＋3×5，
1×5＋3×6＋4×7>1×6＋3×5＋4×7>1×7＋3×6＋4×5.
①若两组数a1，a2与b1，b2，且a1≤a2，b1≤b2，则a1b1＋a2b2≥a1b2＋a2b1是否成立，试证明；
②若两组数a1，a2，a3与b1，b2，b3且a1≤a2≤a3，b1≤b2≤b3，对a1b3＋a2b2＋a3b1，a1b2＋a2b1＋a3b3，a1b1＋a2b2＋a3b3进行大小顺序(不需要说明理由).依据
如果a>b⇔a－b>0.
如果a＝b⇔a－b＝0.
如果ac⇒a>c
不可逆
3
可加性
a>b⇔a＋c>b＋c
可逆
4
可乘性
eq \b\lc\ \rc\}(\a\vs4\al\c1(a>b,c>0))⇒ac>bc
c的符号
eq \b\lc\ \rc\}(\a\vs4\al\c1(a>b,cd))⇒a＋c>b＋d
同向
6
同向同正可乘性
eq \b\lc\ \rc\}(\a\vs4\al\c1(a>b>0,c>d>0))⇒ac>bd
同向
7
可乘方性
a>b>0⇒an>bn(n∈N，n≥2)
同正
【答案详解】
1．D
【详解】
对A，当时，不成立，故A错误；
对B，当时，不成立，故B错误；
对C，当时，不成立，故C错误；
对D，因为为增函数，故时一定成立，故D正确；
故选：D
2．D
【解析】
【分析】
根据条件，结合结合不等式性质判断A，B，C正确，再举例说明D错误..
【详解】
因为，所以，，，，
又，所以，所以成立，
，所以，
，所以，
取可得，，，所以不成立，
故选：D.
3．D
【解析】
【分析】
根据不等式的性质判断．
【详解】
，A错，B错；
即，C错；
，D正确．
故选：D．
4．A
【解析】
【分析】
由，，依题意可得只需比较与的大小，再根据充分条件、必要条件的定义判断可得；
【详解】
解：因为，
又，则，
所以要比较与的大小，即比较与的大小，
即比较与的大小，
当且时，且，
即，所以，即，故充分性成立，
当时，此时也满足，故必要性不成立；
即“”是“”充分不必要条件；
故选：A
5．D
【解析】
【分析】
利用不等式的性质可判断ABD，取特殊值可判断C选项.
【详解】
选项A：因为，所以，
所以，故A错误；
选项B：因为，则，
所以，即，
又，所以不等式
两侧同时乘以，则，故B错误；
选项C：当时，此时，
，，
，故C错误；
选项D：因为，所以，
则 ，故D正确.
故选：D.
6．C
【详解】
解：因为，
所以，，故AB错误；
，所以，
所以，所以，
即，故C正确；
对于D，若时，
则，故D错误.
故选：C.
7．B
【详解】
解：因为
，
所以．
故选：B.
8．D
【解析】
【分析】
首先配方判断、均大于零，然后作商即可比较大小.
【详解】
，
，
则
.
故，当且仅当时，取等号，
故选：D
【点睛】
本题考查了作商法比较两个式子的大小，属于基础题.
9．C
【解析】
【分析】
结合特殊值、差比较法确定正确选项.
【详解】
A：令，；，，则，，不满足，故A错误；
B：a，b异号时，不等式不成立，故B错误；
C：，，，，即，故C正确；
D：令，，不成立，故D错误.
故选：C
10．A
【解析】
【分析】
先求的范围，再根据不等式的性质，求的范围.
【详解】
因为，所以，
由，得.
故选：A.
11．C
【解析】
【分析】
由不等式的性质求解
【详解】
，
故，，得
故选：C
12．A
【解析】
【分析】
根据给定条件解不等式，再分类等价转化即可求解作答.
【详解】
因，则有，解得：或，
当时，，显然不成立，无解，
当时，，不等式恒成立，解得或，则有，
所以使不等式成立的x的取值范围是.
故选：A
13．(1)证明见解析
(2)证明见解析
【解析】
【分析】
（1）可知，而，即可得证；
（2）可知，而，即可得证；
(1)
证明： ，
，
又，
；
(2)
证明：，
，
又，
．
14．(1)证明见解析
(2)证明见解析
(3)证明见解析
【解析】
【分析】
（1）将变为，利用不等式同向正值的可乘性，即可证明结论；
（2）由以及，可得，再根据，同号，得，利用不等式同向正值的可乘性证明结论；
（3）由可得，继而可得,利用不等式的性质可得结论.
(1)
证明：因为，所以，
又，故，
即；
(2)
证明：因为，，所以 ，
因为，同号，所以 ，，
故，即 ，所以；
(3)
证明：因为，所以 ，
又，所以 ，
故.
15．详见解析.
【解析】
【分析】
（1）利用基本不等式即证；
（2）利用不等式的性质，由，可得0，c－b>0，∴
.
50．(1)证明见解析
(2)证明见解析
【解析】
【分析】
（1）根据不等式的性质证明即可；
（2）结合（1）和不等式的性质求解.
(1)
证明：因为，，
所以
所以；
(2)
证明：由（1）得，
又，所以.
51．（1）证明见解析；（2）证明见解析；（3）①成立，证明见解析；②a1b3＋a2b2＋a3b1≤a1b2＋a2b1＋a3b3≤a1b1＋a2b2＋a3b3
【详解】
证明：（1）因为，所以，
又，即，
所以，所以，即≤；
（2）因为，所以，，
所以，
所以；
（3）解：①成立，证明如下：
∵a1b1＋a2b2－(a1b2＋a2b1)＝a1(b1－b2)＋a2(b2－b1)＝(a1－a2)(b1－b2)，
又a1≤a2，b1≤b2，∴(a1－a2)(b1－b2)≥0，即a1b1＋a2b2≥a1b2＋a2b1；
②a1b3＋a2b2＋a3b1≤a1b2＋a2b1＋a3b3≤a1b1＋a2b2＋a3b3