高中数学人教A版 (2019)必修 第一册5.7 三角函数的应用习题

这是一份高中数学人教A版 (2019)必修 第一册5.7 三角函数的应用习题，共36页。试卷主要包含了三角函数模型的作用，函数f，已知f等内容，欢迎下载使用。

知识点一 三角函数的应用
1．三角函数模型的作用
三角函数作为描述现实世界中周期现象的一种数学模型，可以用来研究很多问题，在刻画周期变化规律、预测未来等方面发挥重要作用．
2．用函数模型解决实际问题的一般步骤
收集数据―→画散点图―→选择函数模型―→求解函数模型―→检验．
知识点二 函数y＝Asin(ωx＋φ)，A>0，ω>0中参数的物理意义
三角函数在物理中的应用
函数的周期，振幅，初相分别是
A．B．C．D．
三角函数的振幅和最小正周期分别为
A．，B．，C．，D．，
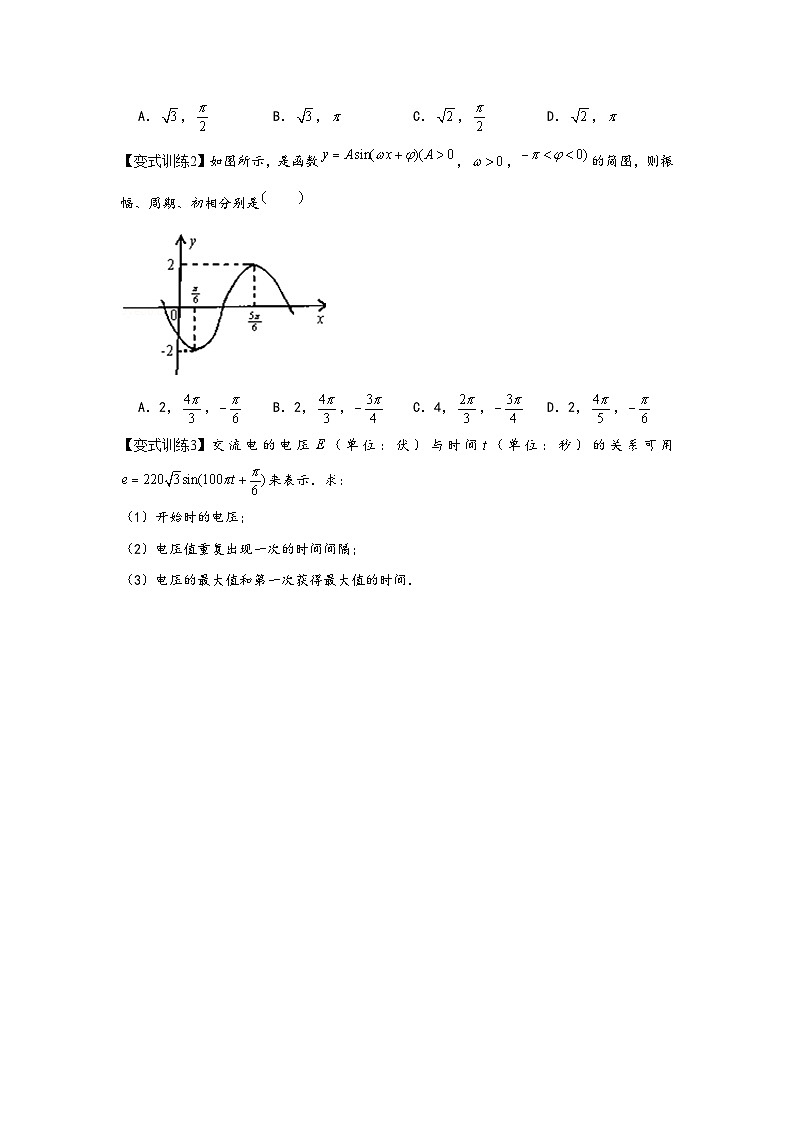
如图所示，是函数，，的简图，则振幅、周期、初相分别是
A．2，，B．2，，C．4，，D．2，，
交流电的电压（单位：伏）与时间（单位：秒）的关系可用来表示．求：
（1）开始时的电压；
（2）电压值重复出现一次的时间间隔；
（3）电压的最大值和第一次获得最大值的时间．
三角函数在生活中的应用
弹簧挂着的小球做上下运动，它在秒时相对于平衡位置厘米有下列关系确定．
（1）以为横坐标，为纵坐标，作出这个函数在一个周期内的图象；
（2）小球在开始振动时的位置在哪里？
（3）小球的最高点和最低点与平衡位置的距离分别是多少？
（4）经过多少时间小球往复运动一次？
（5）每秒钟小球能往复振动多少次？
摩天轮常被当作一个城市的地标性建筑，如深圳前海的“湾区之光”摩天轮．如图所示，某摩天轮最高点距离地面128米，转盘直径为120米，设置若干个座舱，游客从离地面最近的位置进舱，开启后按逆时针匀速旋转分钟后，游客距离地面的高度为米，满足．若在，时刻，游客距离地面的高度相等，则的最小值为
A．15B．30C．45D．60
唐代李皋发明了“桨轮船”，这种船是原始形态的轮船，是近代明轮航行模式之先导．如图，某桨轮船的轮子的半径为，它以的角速度逆时针旋转．轮子外边沿有一点，点到船底的距离是（单位：，轮子旋转时间为（单位：．当时，点在轮子的最高点处．
（1）当点第一次入水时， ；
（2）当时， ．，
已知是半径为的圆形砂轮边缘上的一个质点，它从初始位置开始，按逆时针方向做圆周运动，角速度为．如图，以砂轮圆心为原点，建立平面直角坐标系，若，则点的纵坐标关于时间（单位：的函数关系式为
A．B．
C．D．
一半径为2米的水轮如图所示，水轮圆心距离水面1米，已知水轮每60秒逆时针匀速转动一圈，如果当水轮上点从水中浮现时（图中点开始计时，则点距离水面的高度（米与（秒的一个函数解析式为
A．B．
C．D．
某高校专家楼前现有一块矩形草坪，已知草坪长米，宽米，为了便于专家平时工作、起居，该高校计划在这块草坪内铺设三条小路、和，并要求是的中点，点在边上，点在边上，且为直角，如图所示．
（Ⅰ）设（弧度），试将三条路的全长（即的周长）表示成的函数，并求出此函数的定义域；
（Ⅱ）这三条路，每米铺设预算费用均为400元，试问如何设计才能使铺路的总费用最低？并求出最低总费用（结果保留整数）（可能用到的参考值：取1.732，取．
学校拟在一块三角形边角地上建外籍教室和留学生公寓楼，如图，已知中，，，．在它的内接正方形中建房，其余部分绿化，假设的面积为，正方形的面积为．
（1）用，表示和；
（2）设，试求的最大值；
某工厂生产主要产品后，留下大量圆心角为，半径为的扇形边角料，现要废物利用，从中剪裁出矩形毛坯，要求矩形面积尽可能大，并如图设计了两种裁剪方法，一种是使矩形的一边落在扇形的半径上，另一种是使矩形的两顶点分别在扇形的两条半径上，请选出最佳方案．
长春某日气温是时间，单位：小时）的函数，下面是某天不同时间的气温预报数据：
根据上述数据描出的曲线如图所示，经拟合，该曲线可近似地看成余弦型函数的图象．
（1）根据以上数据，试求，，的表达式；
（2）大数据统计显示，某种特殊商品在室外销售可获3倍于室内销售的利润，但对室外温度要求是气温不能低于．根据（1）中所得模型，一个24小时营业的商家想获得最大利润，应在什么时间段（用区间表示）将该种商品放在室外销售，单日室外销售时间最长不能超过多长时间？（忽略商品搬运时间及其它非主要因素，理想状态下．
某园林公司计划在一块以为圆心，为常数，单位为米）为半径的半圆形（如图）地上种植花草树木，其中弓形区域用于观赏样板地，区域用于种植花木出售，其余区域用于种植草皮出售．已知观赏样板地的成本是每平方米2元，花木的利润是每平方米8元，草皮的利润是每平方米3元．
（1）设（单位：弧度），用表示弓形的面积；
（2）园林公司应该怎样规划这块土地，才能使总利润最大？并求相对应的．
（参考公式：扇形面积公式，表示扇形的弧长）
一．选择题（共8小题）
1．若函数f（x）＝sin（ωx+φ）的部分图象如图所示，则ω和φ的值可以是（ ）
A．ω=12，φ=π6B．ω=12，φ=−π6C．ω＝1，φ=π3D．ω＝1，φ=−π3
2．已知f（x）＝sinx+acsx，实数x0满足对于任意的x∈R，都有f（x）≤f（x0），若tanx0＝3，则实数a的值为（ ）
A．﹣3B．3C．−13D．13
3．函数f（x）＝Asin（ωx+φ）（A＞0，ω＞0，|φ|＜π2）的部分图象如图所示，则ω，φ的值分别为（ ）
A．2，0B．2，π4C．2，−π3D．2，π6
4．已知f（x）＝sin（ωx+π6）（ω∈Z）x∈（0，π3]时f（x）=12有唯一解，则满足条件的ω的个数是（ ）
A．3B．4C．5D．6
5．已知A是函数f(x)=3sinωx(ω＞0)图象的一个最高点，B，C为直线y=32与函数f（x）图象的两个相邻的交点，若存在B，C，使得△ABC是等边三角形，则ω＝（ ）
A．23B．2C．2π3D．23π3
6．已知x为锐角，a−csxsinx=3，则a的取值范围为（ ）
A．（1，2]B．(1，3)C．[﹣2，2]D．（1，2）
7．如图，摩天轮是一种大型转轮状的机械建筑设施，游客坐在摩天轮的座舱里慢慢地往上转，可以从高处俯瞰四周景色．某摩天轮最高点距离地面高度为120m，转盘直径为110m设置有48个座舱，开启后按逆时针方向匀速旋转，游客在座舱转到距离地面最近的位置进舱，转一周大约需要20min．游客甲坐上摩天轮的座舱，开始转动tmin后距离地面的高度为Hm，则在转动一周的过程中，高度H关于时间t的函数解析式是（ ）
A．H=55cs(π10t−π2)+65(0≤t≤20)
B．H=55sin(π10t−π2)+65(0≤t≤20)
C．H=55cs(π10t+π2)+65(0≤t≤20)
D．H=55sin(π10t+π2)+65(0≤t≤20)
8．如图，飞机飞行的航线AB和地面目标C在同一铅直平面内，在A处测得目标C的俯角为30°，飞行10千米到达B处，测得目标C的俯角为75°，这时B处与地面目标C的距离为（ ）
A．5千米B．52千米C．4千米D．42千米
二．填空题（共4小题）
9．若函数y＝sin（ωx+φ）（ω＞0）的部分图象如图，则ω＝ ．
10．振动量y=2sin（ωx+φ）（ω＞0）的初相和频率分别是﹣π和32，则它的相位是 ．
11．函数f（x）＝2sin（ωx+φ）（ω＞0，0＜φ＜π）的部分图象如图所示，其中f(0)=f(5π9)，f(−2π9)=0，若对于任意的x1∈[−π9，π6)，x2∈(π6，π3)，f（x1）﹣λ＞cs2x2﹣sin3x1恒成立，则实数λ的取值范围为 ．
12．一辆汽车以每小时40千米的速度在公路上（公路是笔直的，不考虑公路的宽度）由东向西行驶，在A处看建筑物P在汽车的北偏西60°，1小时后，汽车行驶到B处，在B处看建筑物P在汽车的北偏西15°，则建筑物P距离该公路 千米．
三．解答题（共3小题）
13．函数f(x)=Asin(ωx+φ)(A＞0，ω＞0，|φ|＜π2，x∈R)的部分图象如图，M是图象的一个最低点，图象与x轴的一个交点的坐标为(π2，0)，与y轴的交点坐标为(0，−2)．
（Ⅰ）求A，ω，φ的值；
（Ⅱ）若关于x的方程f（x）﹣m＝0在[0，2π]上有一解，求实数m的取值范围．
14．已知函数f(x)=Asin(ωx+π6)(A＞0，ω＞0)的部分图象如图所示．
（1）求A，ω的值；
（2）求f（x）的单调增区间；
（3）求f（x）在区间[−π6，π4]上的最大值和最小值．
15．已知函数f（x）=2cs（2x−π4）．
（1）求函数f（x）的最小正周期、单调区间；
（2）求函数f（x）在区间[−π8，π2]上的最小值和最大值．
（时
0
3
6
9
12
15
18
21
24
15.7
14.0
15.7
20.0
24.2
26.0
24.2
20.0
15.7
专题5.7 三角函数的应用
知识点一 三角函数的应用
1．三角函数模型的作用
三角函数作为描述现实世界中周期现象的一种数学模型，可以用来研究很多问题，在刻画周期变化规律、预测未来等方面发挥重要作用．
2．用函数模型解决实际问题的一般步骤
收集数据―→画散点图―→选择函数模型―→求解函数模型―→检验．
知识点二 函数y＝Asin(ωx＋φ)，A>0，ω>0中参数的物理意义
三角函数在物理中的应用
函数的周期，振幅，初相分别是
A．B．C．D．
【解答】解：函数
振幅是2，初相是
又的系数是，故函数的周期是
对照四个选项知应选
故选：．
三角函数的振幅和最小正周期分别为
A．，B．，C．，D．，
【解答】解：
，
三角函数的振幅和最小正周期分别为：，．
故选：．
如图所示，是函数，，的简图，则振幅、周期、初相分别是
A．2，，B．2，，C．4，，D．2，，
【解答】解：由图知周期，，
又因为，知；
再将点，代入，计算求出，
故选：．
交流电的电压（单位：伏）与时间（单位：秒）的关系可用来表示．求：
（1）开始时的电压；
（2）电压值重复出现一次的时间间隔；
（3）电压的最大值和第一次获得最大值的时间．
【解答】解：（1）由题意，开始时的电压；
（2），
电压值重复出现一次的时间间隔；
（3）由题意，电压的最大值为，
由得，，
故第一次获得最大值的时间为．
三角函数在生活中的应用
弹簧挂着的小球做上下运动，它在秒时相对于平衡位置厘米有下列关系确定．
（1）以为横坐标，为纵坐标，作出这个函数在一个周期内的图象；
（2）小球在开始振动时的位置在哪里？
（3）小球的最高点和最低点与平衡位置的距离分别是多少？
（4）经过多少时间小球往复运动一次？
（5）每秒钟小球能往复振动多少次？
【解答】解：（1）由题意可得的图象，
（2）由题意可得当时，，
故小球在开始振动时的位置在，
（3）由解析式可得振幅，
故小球的最高点和最低点与平衡位置的距离均为2（厘米）；
（4）可得函数的周期为，故小球往复运动一次需，
（5）可得频率为，即每秒钟小球能往复振动次
摩天轮常被当作一个城市的地标性建筑，如深圳前海的“湾区之光”摩天轮．如图所示，某摩天轮最高点距离地面128米，转盘直径为120米，设置若干个座舱，游客从离地面最近的位置进舱，开启后按逆时针匀速旋转分钟后，游客距离地面的高度为米，满足．若在，时刻，游客距离地面的高度相等，则的最小值为
A．15B．30C．45D．60
【解答】解：由题意得当时，取得最小值，当，即时，取得最大值128，
由对称性可知当时，，
故选：．
唐代李皋发明了“桨轮船”，这种船是原始形态的轮船，是近代明轮航行模式之先导．如图，某桨轮船的轮子的半径为，它以的角速度逆时针旋转．轮子外边沿有一点，点到船底的距离是（单位：，轮子旋转时间为（单位：．当时，点在轮子的最高点处．
（1）当点第一次入水时， ；
（2）当时， ．，
【解答】解：如图所示，当第一次入水时到达点，由几何关系知，又圆的半径为3，故，
此时轮子旋转的圆心角为：，故；
由题可知，其中，
即，
当时，．
故答案为：
已知是半径为的圆形砂轮边缘上的一个质点，它从初始位置开始，按逆时针方向做圆周运动，角速度为．如图，以砂轮圆心为原点，建立平面直角坐标系，若，则点的纵坐标关于时间（单位：的函数关系式为
A．B．
C．D．
【解答】解：设点的纵坐标关于时间 （单位：的函数关系式为，
由题意可得，，
时，射线可视角的终边，则．
故选：．
一半径为2米的水轮如图所示，水轮圆心距离水面1米，已知水轮每60秒逆时针匀速转动一圈，如果当水轮上点从水中浮现时（图中点开始计时，则点距离水面的高度（米与（秒的一个函数解析式为
A．B．
C．D．
【解答】解：设点距离水面的高度为（米和（秒的函数解析式为，，，
由题意，，，
所以，解得，
由，得，
所以．
当时，，
所以，则，
又因为，所以．
则．
故选：．
某高校专家楼前现有一块矩形草坪，已知草坪长米，宽米，为了便于专家平时工作、起居，该高校计划在这块草坪内铺设三条小路、和，并要求是的中点，点在边上，点在边上，且为直角，如图所示．
（Ⅰ）设（弧度），试将三条路的全长（即的周长）表示成的函数，并求出此函数的定义域；
（Ⅱ）这三条路，每米铺设预算费用均为400元，试问如何设计才能使铺路的总费用最低？并求出最低总费用（结果保留整数）（可能用到的参考值：取1.732，取．
【解答】解：（Ⅰ）在中，，，，
在中，，，，
．
又，
，
三条路的全长（即的周长）．
当点在点时，这时角最小，求得此时；
当点在点时，这时角最大，求得此时．
故此函数的定义域为，；
（Ⅱ）由题意知，要求铺路总费用最低，只要求的周长的最小值即可．
由（Ⅰ）得，，，
设，则，
由，，，
得，
从而，当，即时，，
所以当米时，铺路总费用最低，最低总费用为96560元．
学校拟在一块三角形边角地上建外籍教室和留学生公寓楼，如图，已知中，，，．在它的内接正方形中建房，其余部分绿化，假设的面积为，正方形的面积为．
（1）用，表示和；
（2）设，试求的最大值；
【解答】解：（1）由题意知，，
所以的面积为：
，其中；
又，
所以，
，
所以正方形的面积为：
，其中；
（2）由题意知，其中，
所以；
由，，
所以，
即，当且仅当，即时“”成立；
所以的最大值为．
某工厂生产主要产品后，留下大量圆心角为，半径为的扇形边角料，现要废物利用，从中剪裁出矩形毛坯，要求矩形面积尽可能大，并如图设计了两种裁剪方法，一种是使矩形的一边落在扇形的半径上，另一种是使矩形的两顶点分别在扇形的两条半径上，请选出最佳方案．
【解答】解：方案一，如图，矩形有两个顶点在半径上，
设，则．
扇形圆心角为，．
由正弦定理，得，
．
故矩形的面积为
．
当．即时，取得最大值．
方案二：如图，矩形有两个顶点分别在扇形的两条半径、上．
设，，，
由正弦定理，得．
．
又．
．
矩形的面积为
，
即在此情况下，时，可求出点，然后作出面积为最大．
由于，
所以第一种方案能使截出的矩形面积最大，即，使取在弧中点，分别向扇形的一条半径作垂线及平行线得到矩形，即为最大矩形．
长春某日气温是时间，单位：小时）的函数，下面是某天不同时间的气温预报数据：
根据上述数据描出的曲线如图所示，经拟合，该曲线可近似地看成余弦型函数的图象．
（1）根据以上数据，试求，，的表达式；
（2）大数据统计显示，某种特殊商品在室外销售可获3倍于室内销售的利润，但对室外温度要求是气温不能低于．根据（1）中所得模型，一个24小时营业的商家想获得最大利润，应在什么时间段（用区间表示）将该种商品放在室外销售，单日室外销售时间最长不能超过多长时间？（忽略商品搬运时间及其它非主要因素，理想状态下．
【解答】（1）根据以上数据知，，解得，；
由，解得，所以；
由时，即，
解得，即，；
所以，；
由，解得；
所以，，；
（2）令，得，
即，；
解得，；
当时，，
所以一个24小时营业的商家想获得最大利润，应在，时间段将该种商品放在室外销售，
且单日室外销售时间最长不能超过（小时）．
某园林公司计划在一块以为圆心，为常数，单位为米）为半径的半圆形（如图）地上种植花草树木，其中弓形区域用于观赏样板地，区域用于种植花木出售，其余区域用于种植草皮出售．已知观赏样板地的成本是每平方米2元，花木的利润是每平方米8元，草皮的利润是每平方米3元．
（1）设（单位：弧度），用表示弓形的面积；
（2）园林公司应该怎样规划这块土地，才能使总利润最大？并求相对应的．
（参考公式：扇形面积公式，表示扇形的弧长）
【解答】解：（1），，．
（2）设总利润为元，草皮利润为元，花木地利润为，观赏样板地成本为，，，
．
设，．上为减函数；上为增函数．
当时，取到最小值，此时总利润最大．
答：所以当园林公司把扇形的圆心角设计成时，总利润最大．
一．选择题（共8小题）
1．若函数f（x）＝sin（ωx+φ）的部分图象如图所示，则ω和φ的值可以是（ ）
A．ω=12，φ=π6B．ω=12，φ=−π6C．ω＝1，φ=π3D．ω＝1，φ=−π3
【解答】解：由函数的图象可知：T=4×(2π3+π3)=4π，
T=2πω，所以ω=12．
函数的图象过（−π3，0），
所以0＝sin[12×(−π3)+ϕ]，所以ϕ=π6．
故选：A．
2．已知f（x）＝sinx+acsx，实数x0满足对于任意的x∈R，都有f（x）≤f（x0），若tanx0＝3，则实数a的值为（ ）
A．﹣3B．3C．−13D．13
【解答】解：由题意及正弦函数的图象可知，x0是f（x）的一个极大值点，
由f′（x0）＝csx0﹣asinx0＝0，得a=1tanx0=13，
故选：D．
3．函数f（x）＝Asin（ωx+φ）（A＞0，ω＞0，|φ|＜π2）的部分图象如图所示，则ω，φ的值分别为（ ）
A．2，0B．2，π4C．2，−π3D．2，π6
【解答】解：由函数的图象可知：3T4=11π12−π6=3π4，T＝π，所以ω＝2，A＝1，
函数的图象经过（π6，1），所以1＝sin（2×π6+φ），因为|φ|＜π2，所以φ=π6．
故选：D．
4．已知f（x）＝sin（ωx+π6）（ω∈Z）x∈（0，π3]时f（x）=12有唯一解，则满足条件的ω的个数是（ ）
A．3B．4C．5D．6
【解答】解：当ω＞0时，
∵x∈（0，π3]，
∴ωx+π6∈（π6，πω3+π6]，
∵f（x）在x∈（0，π3]时，f（x）=12有唯一解，
∴πω3∈[2π3，2π)，即ω∈[2，6），
∵ω∈Z，
∴ω＝2，3，4，5，
当ω＜0时，
∵x∈（0，π3]，
∴ωx+π6∈[πω3+π6，π6)，
∴πω3+π6∈(−11π6，−7π6]，
∴πω3∈(−2π，−4π3]，解得ω∈（﹣6，﹣4]，
又∵ω∈Z，
∴ω＝﹣5，﹣4，
综上ω的值为﹣5，﹣4，2，3，4，5共有6个满足题意，
故选：D．
5．已知A是函数f(x)=3sinωx(ω＞0)图象的一个最高点，B，C为直线y=32与函数f（x）图象的两个相邻的交点，若存在B，C，使得△ABC是等边三角形，则ω＝（ ）
A．23B．2C．2π3D．23π3
【解答】
解：令3sinωx=32，
则方程在[0，πω]的解为π6ω，5π6ω，
由△ABC是等边三角形，
则5π6ω−π6ω=2×(3−32)×33=1，
则ω=2π3，
故选：C．
6．已知x为锐角，a−csxsinx=3，则a的取值范围为（ ）
A．（1，2]B．(1，3)C．[﹣2，2]D．（1，2）
【解答】解：x为锐角，a−csxsinx=3，
考点a＝csx+3sinx＝2sin（x+π6），
x+π6∈（π6，2π3），
2sin（x+π6）∈（1，2]．
故选：A．
7．如图，摩天轮是一种大型转轮状的机械建筑设施，游客坐在摩天轮的座舱里慢慢地往上转，可以从高处俯瞰四周景色．某摩天轮最高点距离地面高度为120m，转盘直径为110m设置有48个座舱，开启后按逆时针方向匀速旋转，游客在座舱转到距离地面最近的位置进舱，转一周大约需要20min．游客甲坐上摩天轮的座舱，开始转动tmin后距离地面的高度为Hm，则在转动一周的过程中，高度H关于时间t的函数解析式是（ ）
A．H=55cs(π10t−π2)+65(0≤t≤20)
B．H=55sin(π10t−π2)+65(0≤t≤20)
C．H=55cs(π10t+π2)+65(0≤t≤20)
D．H=55sin(π10t+π2)+65(0≤t≤20)
【解答】解：如图，设舱座距离地面最近的位置为P，
以轴心Q为原点，与底面平行的直线为x轴，建立直角坐标系，
设t＝0min时，游客甲位于点P（0，﹣55），以OP为终边的角为−π2，
根据转一周大约需要20min，可知座舱转动的角速度为2π20=π10，
则在转动一周的过程中，高度H关于时间t的函数解析式是：
H＝55sin（π10t−π2）+65（0≤t≤20）．
故选：B．
8．如图，飞机飞行的航线AB和地面目标C在同一铅直平面内，在A处测得目标C的俯角为30°，飞行10千米到达B处，测得目标C的俯角为75°，这时B处与地面目标C的距离为（ ）
A．5千米B．52千米C．4千米D．42千米
【解答】解：由题意知，在△ABC中，AB＝10，∠BAC＝30°，∠ACB＝75°﹣30°＝45°，
由正弦定理得BCsin30°=10sin45°，
解得BC=10×1222=52．
∴B处与地面目标C的距离为52千米．
故选：B．
二．填空题（共4小题）
9．若函数y＝sin（ωx+φ）（ω＞0）的部分图象如图，则ω＝ 4 ．
【解答】解：由函数的图象可知，（x0，y0）与（x0+π4，﹣y0），纵坐标相反，而且不是相邻的对称点，
所以函数的周期T＝2（x0+π4−x0）=π2，
所以T=2πω=π2，所以ω＝4．
故答案为：4．
10．振动量y=2sin（ωx+φ）（ω＞0）的初相和频率分别是﹣π和32，则它的相位是 3πx﹣π ．
【解答】解：y=2sin（ωx+φ）（ω＞0）的初相和频率分别是﹣π和32，
所以φ＝﹣π，T=132=23，ω=2πT=2π23=3π，
所以函数的关系式为y=2sin(3πx−π)．
所以它的相位是3πx﹣π，
故答案为：3πx﹣π
11．函数f（x）＝2sin（ωx+φ）（ω＞0，0＜φ＜π）的部分图象如图所示，其中f(0)=f(5π9)，f(−2π9)=0，若对于任意的x1∈[−π9，π6)，x2∈(π6，π3)，f（x1）﹣λ＞cs2x2﹣sin3x1恒成立，则实数λ的取值范围为 （﹣∞，−12] ．
【解答】解：因为f(0)=f(5π9)，所以y＝f（x）的图象关于直线x=5π18对称，
又f(−2π9)=0，由图知3T4=5π18+2π9=π2，
所以T=2π3，从而ω＝3，
由3×（−2π9）+φ＝0，得φ=2π3，
所以f（x）＝2sin（3x+2π3），
f（x1）﹣λ＞cs2x2﹣sin3x1，可化为3cs3x1＞cs2x2+λ，
当x1∈[−π9，π6)，x2∈(π6，π3)时，3cs3x1∈（0，3]，cs2x2+λ∈（λ−12，λ+12），
所以λ+12≤0，解得λ≤−12，即λ∈（﹣∞，−12]．
故答案为：（﹣∞，−12]．
12．一辆汽车以每小时40千米的速度在公路上（公路是笔直的，不考虑公路的宽度）由东向西行驶，在A处看建筑物P在汽车的北偏西60°，1小时后，汽车行驶到B处，在B处看建筑物P在汽车的北偏西15°，则建筑物P距离该公路 103+10 千米．
【解答】解：如图，过点P作PC⊥AB．
由题意可得AB＝40千米，∠PAB＝30°，∠PBA＝105°，
则∠APB＝45°，∠PBC＝75°．
由正弦定理可得：ABsin45°=PBsin30°，则PB=40×1222=202千米．
因为PC⊥AB，所以∠PCB＝90°，
所以PC=202⋅sin75°=103+10千米，
即建筑物P距离该公路103+10千米．
故答案为：103+10．
三．解答题（共3小题）
13．函数f(x)=Asin(ωx+φ)(A＞0，ω＞0，|φ|＜π2，x∈R)的部分图象如图，M是图象的一个最低点，图象与x轴的一个交点的坐标为(π2，0)，与y轴的交点坐标为(0，−2)．
（Ⅰ）求A，ω，φ的值；
（Ⅱ）若关于x的方程f（x）﹣m＝0在[0，2π]上有一解，求实数m的取值范围．
【解答】解：（Ⅰ）由函数f（x）的部分图象可知，函数f（x）的周期为T=4×[π2−(−π2)]=4π，
∴2πω=4π，解得ω=12；
又函数图象与x轴的一个交点坐标为(π2，0)，
∴Asin(12×π2+φ)=0，
∴sin(π4+φ)=0，
∴π4+φ=kπ，k∈Z，即φ=kπ−π4(k∈Z)；
由|φ|＜π2，得−π2＜φ＜π2，
∴φ=−π4；
∴函数y＝f（x）＝Asin（12x−π4）．
当x＝0时，y=Asin(−π4)=−2，
∴A＝2；
综上可知，A＝2，ω=12，φ=−π4．
（Ⅱ）由f（x）﹣m＝0得f（x）＝m，
要使方程f（x）﹣m＝0在x∈[0，2π]上有一解，
只需直线y＝m与函数f（x）的图象在x∈[0，2π]上只有一个交点；
由（Ⅰ）可知f(x)=2sin(12x−π4)，
画出函数f(x)=2sin(12x−π4)在区间[0，2π]上的图象，如图所示；
由图象知，当−2≤m＜2或m＝2时，满足题意，
所以m的取值范围是m∈[−2，2)∪{2}．
14．已知函数f(x)=Asin(ωx+π6)(A＞0，ω＞0)的部分图象如图所示．
（1）求A，ω的值；
（2）求f（x）的单调增区间；
（3）求f（x）在区间[−π6，π4]上的最大值和最小值．
【解答】解：（1）由图象知A＝1，…（2分）
由图象得函数的最小正周期为2(2π3−π6)=π，
则由2πω=π得ω＝2．…（4分）
（2）∵−π2+2kπ≤2x+π6≤π2+2kπ，
∴−2π3+2kπ≤2x≤π3+2kπ．
∴−π3+kπ≤x≤π6+kπ．
所以f（x）的单调递增区间为[−π3+kπ，π6+kπ]，k∈Z．…（9分）
（3）∵−π6≤x≤π4，∵−π3≤2x≤π2，
∴−π6≤2x+π6≤2π3．
∴−12≤sin(2x+π6)≤1．…（12分）
当2x+π6=π2，即x=π6时，f（x）取得最大值1；
当2x+π6=−π6，即x=−π6时，f（x）取得最小值−12．…（14分）
15．已知函数f（x）=2cs（2x−π4）．
（1）求函数f（x）的最小正周期、单调区间；
（2）求函数f（x）在区间[−π8，π2]上的最小值和最大值．
【解答】解：（1）函数f（x）=2cs（2x−π4）中，它的最小正周期为T=2π2=π，
令﹣π+2kπ≤2x−π4≤2kπ，k∈Z，
解得−3π8+kπ≤x≤π8+kπ，k∈Z，
所以f（x）的单调增区间为[−3π8+kπ，π8+kπ]，k∈Z；
令2kπ≤2x−π4≤π+2kπ，k∈Z，
解得π8+kπ≤x≤5π8+kπ，k∈Z，
所以f（x）的单调减区间为[π8+kπ，5π8+kπ]，k∈Z；
（2）x∈[−π8，π2]时，−π4≤2x≤π，所以−π2≤2x−π4≤3π4；
令2x−π4=3π4，解得x=π2，此时f（x）取得最小值为f（π2）=2×（−22）＝﹣1；
令2x−π4=0，解得x=π8，此时f（x）取得最大值为f（π8）=2×1=2．
（时
0
3
6
9
12
15
18
21
24
15.7
14.0
15.7
20.0
24.2
26.0
24.2
20.0
15.7