

2024年江苏省扬州市中考数学试题含答案
展开1. 实数2的倒数是( )
A. B. 2C. D.
2. “致中和,天地位焉,万物育焉”,对称之美随处可见.下列选项分别是扬州大学、扬州中国大运河博物馆、扬州五亭桥、扬州志愿服务的标识.其中的轴对称图形是( )
A B. C. D.
3. 下列运算中正确的是( )
A. B.
C. D.
4. 第8个全国近视防控宣传教育月的主题是“有效减少近视发生,共同守护光明未来”.某校积极响应,开展视力检查.某班45名同学视力检查数据如下表:
这45名同学视力检查数据的众数是( )
A. B. C. D.
5. 在平面直角坐标系中,点关于原点的对称点的坐标是( )
A. B. C. D.
6. 如图是某几何体的表面展开后得到的平面图形,则该几何体是( )
A. 三棱锥B. 圆锥C. 三棱柱D. 长方体
7. 在平面直角坐标系中,函数的图像与坐标轴的交点个数是( )
A. 0B. 1C. 2D. 4
8. 1202年数学家斐波那契在《计算之书》中记载了一列数:1,1,2,3,5,……,这一列数满足:从第三个数开始,每一个数都等于它前两个数之和.则在这一列数的前2024个数中,奇数的个数为( )
A. 676B. 674C. 1348D. 1350
二、填空题(本大题共有10小题,每小题3分,共30分.不需写出解答过程,请把答案直接填写在答题卡相应位置上)
9. 近年来扬州经济稳步发展:2024年4月26日,扬州市统计局、国家统计局扬州调查队联合发布一季度全市实现地区生产总值约18700000万元,把18700000这个数用科学记数法表示为____.
10. 分解因式:_____.
11. 某学习小组做抛掷一枚瓶盖的实验,整理的实验数据如表:
随着实验次数的增大,“盖面朝上”的概率接近于__________(精确到0.01).
12. 若二次根式有意义,则x的取值范围是___.
13. 若用半径为的半圆形纸片围成一个圆锥的侧面,则这个圆锥底面圆的半径为____.
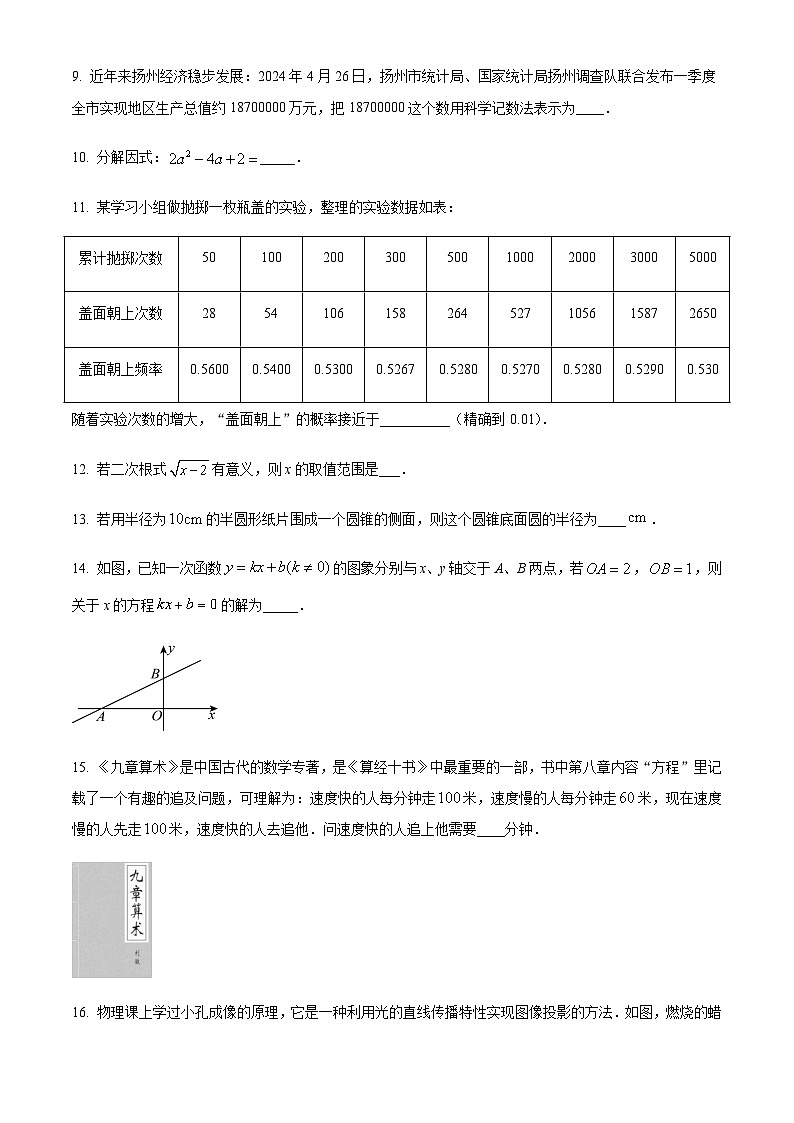
14. 如图,已知一次函数的图象分别与x、y轴交于A、B两点,若,,则关于x的方程的解为_____.
15. 《九章算术》是中国古代的数学专著,是《算经十书》中最重要的一部,书中第八章内容“方程”里记载了一个有趣的追及问题,可理解为:速度快的人每分钟走米,速度慢的人每分钟走米,现在速度慢的人先走米,速度快的人去追他.问速度快的人追上他需要____分钟.
16. 物理课上学过小孔成像的原理,它是一种利用光的直线传播特性实现图像投影的方法.如图,燃烧的蜡烛(竖直放置)经小孔在屏幕(竖直放置)上成像.设,.小孔到的距离为,则小孔到的距离为_____.
17. 如图,在平面直角坐标系中,点A的坐标为,点B在反比例函数的图像上,轴于点C,,将沿翻折,若点C的对应点D落在该反比例函数的图像上,则k的值为_____.
18. 如图,已知两条平行线、,点A是上的定点,于点B,点C、D分别是、上的动点,且满足,连接交线段于点E,于点H,则当最大时,的值为_____.
三、解答题(本大题共有10小题,共96分.请在答题卡指定区域内作答,解答时应写出必要的文字说明、证明过程或演算步骤)
19. (1)计算:;
(2)化简:.
20. 解不等式组,并求出它的所有整数解的和.
21. 2024年5月28日,神舟十八号航天员叶光富、李聪、李广苏密切协同,完成出舱活动,活动时长达8.5小时,刷新了中国航天员单次出舱活动时间纪录,进一步激发了青少年热爱科学的热情.某校为了普及“航空航天”知识,从该校1200名学生中随机抽取了200名学生参加“航空航天”知识测试,将成绩整理绘制成如下不完整的统计图表:
成绩统计表
成绩条形统计图
根据所给信息,解答下列问题:
(1)本次调查的成绩统计表中________%,并补全条形统计图;
(2)这200名学生成绩的中位数会落在________组(填A、B、C、D或E);
(3)试估计该校1200名学生中成绩在90分以上(包括90分)的人数.
22. 2024年“五一”假期,扬州各旅游景区持续火热.小明和小亮准备到东关街、瘦西湖、运河三湾风景区、个园、何园(分别记作A、B、C、D、E)参加公益讲解活动.
(1)若小明在这5个景区中随机选择1个景区,则选中东关街的概率是______;
(2)小明和小亮在C、D、E三个景区中,各自随机选择1个景区,请用画树状图或列表的方法,求小明和小亮选到相同景区的概率.
23. 为了提高垃圾处理效率,某垃圾处理厂购进A、B两种机器,A型机器比B型机器每天多处理40吨垃圾,A型机器处理500吨垃圾所用天数与B型机器处理300吨垃圾所用天数相等.B型机器每天处理多少吨垃圾?
24. 如图1,将两个宽度相等的矩形纸条叠放在一起,得到四边形.
(1)试判断四边形的形状,并说明理由;
(2)已知矩形纸条宽度为,将矩形纸条旋转至如图2位置时,四边形的面积为,求此时直线所夹锐角的度数.
25. 如图,已知二次函数的图像与轴交于,两点.
(1)求的值;
(2)若点在该二次函数的图像上,且的面积为,求点的坐标.
26 如图,已知及边上一点.
(1)用无刻度直尺和圆规射线上求作点,使得;(保留作图痕迹,不写作法)
(2)在(1)的条件下,以点为圆心,以为半径的圆交射线于点,用无刻度直尺和圆规在射线上求作点,使点到点的距离与点到射线的距离相等;(保留作图痕迹,不写作法)
(3)在(1)、(2)的条件下,若,,求的长.
27. 如图,点依次在直线上,点固定不动,且,分别以为边在直线同侧作正方形、正方形,,直角边恒过点,直角边恒过点.
(1)如图,若,,求点与点之间的距离;
(2)如图,若,当点在点之间运动时,求的最大值;
(3)如图,若,当点在点之间运动时,点随之运动,连接,点是的中点,连接,则的最小值为_______.
28. 在综合实践活动中,“特殊到一般”是一种常用方法,我们可以先研究特殊情况,猜想结论,然后再研究一般情况,证明结论.
如图,已知,, 是的外接圆,点在上(),连接、、.
【特殊化感知】
(1)如图1,若,点在延长线上,则与的数量关系为________;
【一般化探究】
(2)如图2,若,点、在同侧,判断与的数量关系并说明理由;
【拓展性延伸】
(3)若,直接写出、、满足数量关系.(用含的式子表示)
参考答案
一、选择题(本大题共有8小题,每小题3分,共24分.在每小题所给出的四个选项中,恰有一项是符合题目要求的,请将该选项的字母代号填涂在答题卡相应位置上)
1. 【答案】D
【解析】解:∵,
∴的倒数为,
故选:D .
2. 【答案】C
【解析】解:A,B,D选项中的图形都不能找到一条直线,使图形沿一条直线折叠,直线两旁的部分能够互相重合,所以不是轴对称图形;
C选项中的图形能找到一条直线,使图形沿一条直线折叠,直线两旁的部分能够互相重合,所以是轴对称图形;
故选:C.
3. 【答案】B
【解析】解:A、,原选项错误,不符合题意;
B、,正确,符合题意;
C、,原选项错误,不符合题意;
D、,原选项错误,不符合题意;
故选:B .
4. 【答案】B
【解析】解:这45名同学视力检查数据中,出现的次数最多,因此众数是.
故选:B.
5. 【答案】D
【解析】∵点关于原点的对称点为,
∴的坐标为(-1,-2),
故选D.
6. 【答案】C
【解析】解:根据图示,上下是两个三角形,中间是长方形,
∴三棱柱,
故选:C .
7. 【答案】B
【解析】当时,,
∴与y轴的交点为;
由于是分式,且当时,,即,
∴与x轴没有交点.
∴函数的图像与坐标轴的交点个数是1个,
故选:B.
8. 【答案】D
【解析】这一列数为:1,1,2,3,5,8,13,21,34,…
可以发现每3个数为一组,每一组前2个数为奇数,第3个数为偶数.
由于,
即前2024个数共有674组,且余2个数,
∴奇数有个.
故选:D
二、填空题(本大题共有10小题,每小题3分,共30分.不需写出解答过程,请把答案直接填写在答题卡相应位置上)
9. 【答案】
【解析】,
故答案为:.
10. 【答案】
【解析】解:先提取公因式2后继续应用完全平方公式分解即可:
原式,
故答案为:.
11. 【答案】0.53
【解析】解:由表中数据可得:随着实验次数的增大,“盖面朝上”的概率接近0.53,
故答案:0.53
12. 【答案】
【解析】解:根据题意,使二次根式有意义,即x﹣2≥0,
解得:x≥2.
故答案为:x≥2.
13. 【答案】5
【解析】解:圆锥的侧面展开图的弧长为,
∴圆锥的底面半径为,
故答案为:5.
14. 【答案】
【解析】解:∵,
∴,
∵一次函数图象与轴交于点,
∴当时,,即时,,
∴关于的方程的解是.
故答案为:.
15. 【答案】
【解析】解:根据题意,设分钟追上,
∴,
解得,,
∴速度快的人追上速度慢的人需要分钟,
故答案为: .
16. 【答案】
【解析】由题意得:,
∴,
如图,过作于点,交于点,
∴,,
∴,即,
∴(),
即小孔到的距离为,
故答案为:.
17. 【答案】
【解析】解:如图,过点作轴于点.
∵点A的坐标为,
∴,
∵,,
设,则,
由对称可知,,
∴,
∴,,
∴,
∵点B的对应点D落在该反比例函数的图像上,
∴,
解得:,
∵反比例函数图象在第一象限,
∴,
故答案为:.
18. 【答案】
【解析】解:∵两条平行线、,点A是上的定点,于点B,
∴点B为定点,的长度为定值,
∵,
∴,,
∵,
∴,
∴,
∵,
∴,
∴点H在以为直径的圆上运动,
如图,取线段的中点O,以点O为圆心,为半径画圆,
则点在上运动,
∴当与相切时最大,
∴,
∵,
∴,
∵,
∴,
故答案为:.
三、解答题(本大题共有10小题,共96分.请在答题卡指定区域内作答,解答时应写出必要的文字说明、证明过程或演算步骤)
19. 【答案】(1);(2)
【解析】解:(1)
;
(2)
.
20. 【答案】,整数和为6
【解析】解:,
由①得,,
解得,;
由②得,,
移项得,,
解得,,
∴原不等式组的解为:,
∴所有整数解为:,
∴所有整数解的和为:.
21. 【答案】(1)20,条形统计图见详解
(2)D (3)300人
【解析】
【小问1详解】
,
C组人数为:,
补全条形统计图如图所示:
故答案为:20
【小问2详解】
,
,
∴200名学生成绩的中位数会落在D组.
【小问3详解】
(人)
估计该校1200名学生中成绩在90分以上(包括90分)的人数为300人.
22. 【答案】(1)
(2)
【解析】
【小问1详解】
解:由题意得从这些景区随机选择1个景区,选中东关街的有1种可能,
∴选中东关街的概率是,
故案䅁为:;
【小问2详解】
列表如下:
共有9种等可能结果,其中小明和小亮选到相同景区的结果有3种结果,
∴小明和小亮选到相同景区的概率:;
答:小明和小亮选到相同景区的概率.
23. 【答案】B型机器每天处理60吨
【解析】解:设型机器每天处理吨垃圾,则型机器每天处理吨垃圾,
根据题意,得,
解得.
经检验,是所列方程的解.
答:B型机器每天处理60吨.
24. 【答案】(1)四边形是菱形,理由见详解
(2)
【解析】
【小问1详解】
解:四边形是菱形,理由如下,
如图所示,过点作于点,过点作于点,
根据题意,四边形,四边形是矩形,
∴,
∴,
∴四边形是平行四边形,
∵宽度相等,即,且,
∴,
∴,
∴平行四边形是菱形;
【小问2详解】
解:如图所示,过点作于点,
根据题意,,
∵,
∴,
由(1)可得四边形是菱形,
∴,
在中,,
∴.
25. 【答案】(1)
(2)
【解析】
【小问1详解】
解:二次函数的图像与轴交于,两点,
∴,
解得,,
∴;
【小问2详解】
解:由(1)可知二次函数解析式为:,,,
∴,
设,
∴,
∴,
∴,
∴当时,,无解,不符合题意,舍去;
当时,,;
∴.
26. 【答案】(1)作图见详解 (2)作图见详解
(3)
【解析】
【小问1详解】
解:如图所示,
∴;
点O即为所求
【小问2详解】
解:如图所示,
连接,以点为圆心,以为半径画弧交于点,以点为圆心,以任意长为半径画弧交于点,分别以点为圆心,以大于为半径画弧,交于点,连接并延长交于点,
∵是直径,
∴,即,
根据作图可得,
∴,即,是点到的距离,
∵,
∴,
∴,
点即为所求点的位置;
【小问3详解】
解:如图所示,
根据作图可得,,连接,
∴在中,,
∴,
∴,
∵是直径,
∴,
∴,
设,则,
∴在中,,
解得,(负值舍去),
∴,
在中,.
27. 【答案】(1)或;
(2);
(3).
【解析】
【小问1详解】
解:设,则,
∵四边形、是正方形,
∴,,,
∴,,
∵,
∴,
∴,
∴,
∴,即,则,
解得:或,
∴或;
【小问2详解】
设,则,
∵四边形、是正方形,
∴,,,
∴,,
∵,
∴,
∴,
∴,
∴,即,
∴,
当时,有最大,最大值为;
【小问3详解】
连接,
∵四边形是正方形,
∴,
即点在对角线所在直线上运动,
如图,作关于的对称点,连接,过作于点,
∴,四边形为矩形,
则点三点共线,,
∴,
∴,
∵,点是的中点,
∴,
∴,
∴当三点共线时,有最小值,
∴在中,由勾股定理得:,
∴的最小值为,
故答案为:.
28. 【答案】(1);(2)(3)当在上时,;当在上时,
【解析】解:∵,,
∴是等边三角形,则
∵是的外接圆,
∴是的角平分线,则
∴
∵四边形是圆内接四边形,
∴
∴
设交于点,则,
设,则
在中,
∴
∴,
∵是直径,则,
在中,
∴
∴
(2)如图所示,在上截取,
∵
∴
∴是等边三角形,
∴,则
∴
∵四边形是圆内接四边形,
∴
∴;
∵,,
∴是等边三角形,则
∴,
又∵
∴
在中
∴
∴,
∴
即;
(3)解:①如图所示,当在上时,
在上截取,
∵
∴
又∵
∴,则
∴即
又∵
∴
∴
∴
∵
∴
如图所示,作于点,
在中,,
∴
∴
∴,即
②当在上时,如图所示,延长至,使得,连接,
∵四边形是圆内接四边形,
∴
又∵
∴,则
∴即,
又∵
∴
∴
∴,
∵
同①可得
∴
∴
综上所述,当在上时,;当在上时,.
注意事项
考生在答题前请认真阅读本注意事项及各题答题要求
1.本试卷共6页,包含选择题(第1题~第8题,共8题)、非选择题(第9题~第28题,共20题)两部分.本卷满分150分,考试时间为120分钟.考试结束后,请将本试卷和答题卡一并交回.
2.答题前,请务必将自己的姓名、准考证号用0.5毫米黑色墨水的签字笔填写在试卷及答题卡的规定位置,在试卷第一面的右下角填写好座位号.
3.请认真核对监考员在答题卡上所粘贴的条形码上的姓名、准考证号与本人是否相符.
4.答选择题,必须用2B铅笔将答题卡上对应选项的方框涂满、涂黑;如需改动,请用橡皮擦干净后,再选涂其他答案.答非选择题,必须用0.5毫米黑色墨水的签字笔在答题卡上的指定位置作答,在其他位置作答一律无效.
5.如需作图,必须用2B铅笔绘、写清楚,线条、符号等须加黑、加粗.
视力
人数
7
4
4
7
11
10
5
3
累计抛掷次数
50
100
200
300
500
1000
2000
3000
5000
盖面朝上次数
28
54
106
158
264
527
1056
1587
2650
盖面朝上频率
0.5600
0.5400
0.5300
0.5267
0.5280
0.5270
0.5280
0.5290
0.530
组别
成绩x(分)
百分比
A组
B组
C组
a
D组
E组
小亮 小明
C
D
E
C
D
E
2024年江苏省扬州市中考数学试题(图片版,含答案): 这是一份2024年江苏省扬州市中考数学试题(图片版,含答案),共7页。试卷主要包含了 10, 20 17, 30°,AD-BD=CD等内容,欢迎下载使用。
2024年江苏省扬州市中考数学试题: 这是一份2024年江苏省扬州市中考数学试题,共6页。
2024年江苏省扬州市中考数学试题: 这是一份2024年江苏省扬州市中考数学试题,共6页。












