河北省石家庄市平山县2023-2024学年七年级下学期期中数学试卷(解析版)

这是一份河北省石家庄市平山县2023-2024学年七年级下学期期中数学试卷(解析版)，共15页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
一、选择题（本大题共12个小题，每小题3分，共36分．在每小题给出的四个选项中，有且仅有一项是符合题目要求的）
1. 如图，下列各角与是内错角的是（ ）

A. B. C. D.
【答案】B
【解析】A、与是同旁内角；
B、与是内错角；
C、与不是内错角；
D、与是同位角；
故选：B．
2. 9的算术平方根是（ ）
A. B. 9C. 3D.
【答案】C
【解析】∵，∴9的算术平方根是3，
故选：C．
3. 如图，点在线段上，则点的纵坐标可能是（ ）
A. B. 4C. 6D.
【答案】B
【解析】观察图象可知，点的纵坐标在和之间，
点的纵坐标可能是，
故选：B．
4. 下列命题不成立的是（ ）
A. 等角补角相等B. 两直线平行,内错角相等
C. 同位角相等D. 对顶角相等
【答案】C
【解析】A. 等角的补角相等，正确．
B. 两直线平行，内错角相等，正确．
C.两直线平行，同位角相等．这是平行线的性质，没有两直线平行的前提，同位角相等，错误．
D.对顶角相等，正确．
故选C．
5. 如图所示，点E在BA的延长线上，点F在BC的延长线上，则下列条件中能判定AB∥CD的是（ ）
A. ∠1＝∠2B. ∠DAE＝∠B
C. ∠D＋∠BCD＝180°D. ∠3＝∠4
【答案】D
【解析】A、当∠1＝∠2时，可得：AD∥BC，故本选项不合题意；
B、当∠DAE＝∠B时，可得AD∥BC，故本选项不合题意；
C、当∠D＋∠BCD＝180°时，可得：AD∥BC，故本选项不合题意；
D、当∠3＝∠4时，可得：AB∥CD，故本选项符合题意；
故选：D．
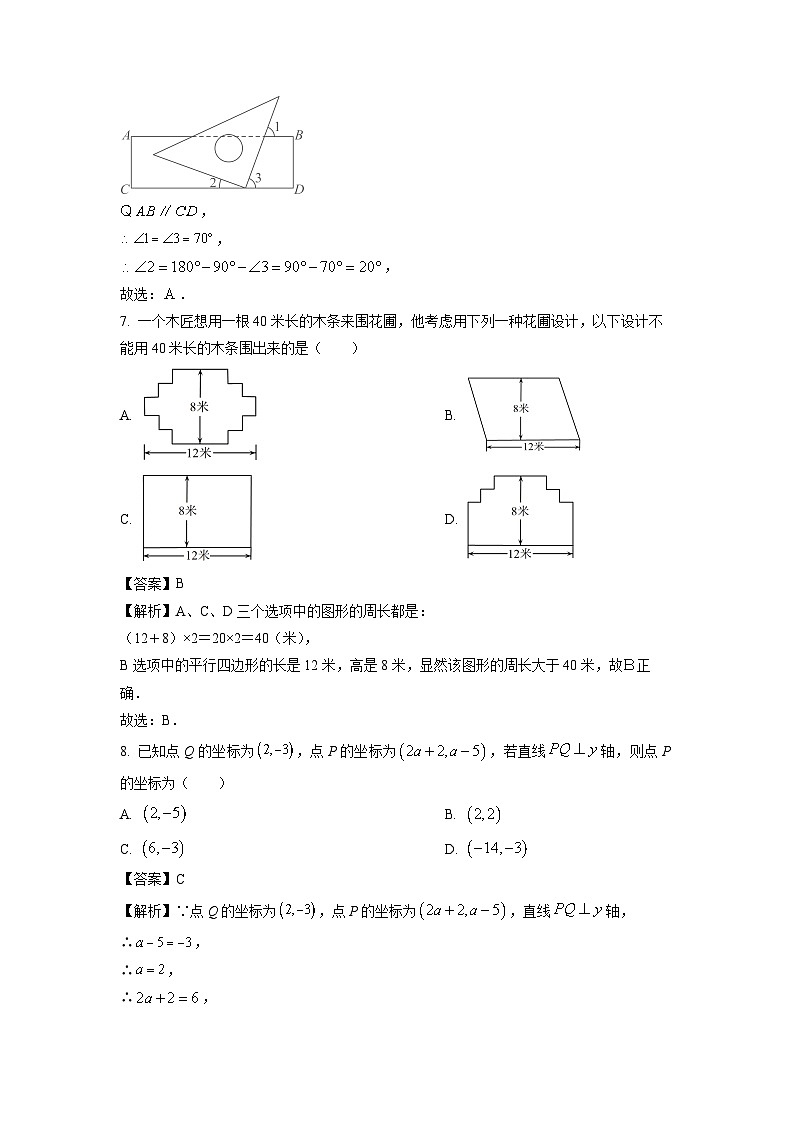
6. 如图，一块直角三角板的直角顶点放在直尺的一边上．如果，那么的度数是（ ）

A. B.
C. D.
【答案】A
【解析】如下图进行标注，

，
，
，
故选：．
7. 一个木匠想用一根40米长的木条来围花圃，他考虑用下列一种花圃设计，以下设计不能用40米长的木条围出来的是（ ）
A. B.
C. D.
【答案】B
【解析】A、C、D三个选项中的图形的周长都是：
（12＋8）×2＝20×2＝40（米），
B选项中的平行四边形的长是12米，高是8米，显然该图形的周长大于40米，故Ｂ正确．
故选：B．
8. 已知点Q的坐标为，点P的坐标为，若直线轴，则点P的坐标为（ ）
A. B.
C. D.
【答案】C
【解析】∵点Q的坐标为，点P的坐标为，直线轴，
∴，
∴，
∴，
∴点P的坐标为．
故选：C．
9. 在一次“寻宝”游戏中，寻宝人已经找到两个标志点和，并且知道藏宝地点的坐标是，则藏宝处应为图中的（ ）
A. 点B. 点C. 点D. 点
【答案】B
【解析】∵点和，∴坐标原点的位置如下图：
∵藏宝地点的坐标是，∴藏宝处应为图中的：点，
故选：B．
10. 小明观察“抖空竹”时发现，可以将某一时刻的情形抽象成数学问题：如图，已知ABCD，∠BAE＝91°，∠DCE＝124°，则∠AEC的度数是（ ）
A. 29°B. 30°C. 31°D. 33°
【答案】D
【解析】延长DC，交AE于点M，如图所示：
∴AB∥CD，
∴∠CME＝∠BAE＝91°，
∴∠AEC＝∠DCE﹣∠CME＝124°﹣91°＝33°．
故选：D．
11. 如图，在一条不完整的数轴上，从左到右的点A、B、C把数轴分成①②③④四部分，点A、B、C对应的实数分别是a、b、c，若原点在第③部分，则下列结论：（1），（2），（3）（4），其中，正确的是（ ）
A. （1）和（2）B. （3）和（4）
C. （2）和（3）D. （1）和（4）
【答案】C
【解析】若原点在第③部分，则a＜0，b＜0，c＞0，a＜b＜0＜c，
（1）∵a＜0，b＜0，∴，
故（1）错误；
（2）∵a＜0，b＜0，∴，
故（2）正确；
（3）∵a＜0，c＞0，∴，
故（3）正确；
（4）∵a＜b＜0，∴，
故（4）错误；
故选：C．
12. 如图，在平面直角坐标系中，从点，，，，，……，依次扩展下去，则的坐标是（ ）
A. B.
C. D.
【答案】D
【解析】，，，，，，，，……
，，，
．
故选：D．
二、填空题（本大题有4个小题，每小题3分，共12分．）
13. 根据下面表格中的数据求出2.5921的平方根是____．
【答案】
【解析】由表格信息可得：当时，则
∵，∴
∴
∴
∴2.5921的平方根是
故答案为：
14. 如图所示，已知，，则______．

【答案】
【解析】如图，
∵，，
∴，
∴，
故答案为：．

15. 如下图所示，在平面直角坐标系中，点P的坐标为，点Q是x轴上的一个动点，当线段的长最小时，点Q的坐标为___________．
【答案】（1，0）
【解析】根据题意得：当PQ⊥x轴时，PQ最小，此时点P、Q的横坐标相同，
∵点P的坐标为，点Q是x轴上的一个动点，
∴当线段的长最小时，点Q的坐标为（1，0）．
故答案为：（1，0）
16. 如图，两个直角三角形重叠在一起，将其中一个沿点B到点C的方向平移到的位置，，，阴影部分的面积为48，则平移距离为______．

【答案】6
【解析】根据平移的性质可知，，，
∵，
∴，
设，
∵，
∴，
∴，
解得．
故答案为： 6．
三、解答题（本大题有8个小题，共72分．解答应写出文字说明、证明过程或演算步骤）
17. 计算：
（1）；（2）．
解：（1）；
（2）.
18. 已知，求证：．

证明：已知
∴（_____________）
已知
∴（_______________）
∴（平行于同一直线的两直线平行）
____________________
解：∵（已知），
∴（内错角相等，两直线平行），
∵（已知），
∴（同位角相等，两直线平行），
∴（平行于同一直线两直线平行），
∴（两直线平行，同旁内角互补），
故答案为：，内错角相等，两直线平行；，同位角相等，两直线平行；，；两直线平行，同旁内角互补．
19. 已知七个实数，，4，，，0，．其中五个数已在数轴上分别用点、、、、表示．
（1）点表示数______，点表示数______，点表示数______，点表示数______；
（2）在数轴上准确地表示数（提示：注意观察正方形的面积），并将所有的数用“＜”连接；
______＜______＜ 0 ＜______＜______＜______＜______．
解：（1）根据在数轴上的位置,可知，点表示数，点表示数，点表示数, 点表示数
故答案为:0，，，4；
（2）在数轴上准确地表示数 如图所示：
由数轴可知，.
20. 如下图所示，在平面直角坐标系中，三角形的顶点均在网格的格点处．
（1）请写出A，B，C的坐标；
（2）三角形的坐标分别为．
①请在图中画出三角形；
②三角形能否由三角形通过平移得到？如果能，请写出平移的过程．
解：（1）根据题意得： A（－3，0），B（－2，2），C（1，1）．
（2）①三角形DEF如图所示．
②能通过平移得到．理由如下：
根据题意得：点A（-3，0）先向右平移1个单位，再向下平移3个单位得到点（-2，-3），点B（-2，2）先向右平移1个单位再向下平移3个单位得到点（-1，-1），点C（1，1）先向右平移1个单位，再向下平移3个单位得到点（2，-2），
∴三角形ABC先向下平移3个单位，再向右平移1个单位（或先向右平移1个单位再向下平移3个单位）即可得到三角形DEF．
21. 如图所示正方形纸板是由两张大小相同的长方形纸板拼接而成的，已知一个长方形纸板的面积为．
（1）求正方形纸板的边长；
（2）若将该正方形纸板进行裁剪，然后拼成一个体积为的正方体，求剩余纸板的面积．
解：（1）正方形纸板的面积为，
所以正方形纸板的边长为．
（2）拼成的体积为的正方体的棱长为，
所以剩余纸板的面积为．
22. 如图，是上一点，，交于点，点在边上，且．

（1）判断，的位置关系，并说明理由；
（2）若，求的度数．
解：（1），理由如下：
∵，
∴
∵，
∴，
∴．
（2）∵，
∴，
∵，
∴，
∵，
∴，
又∵，
∴．
23. 如图，在长方形中，为平面直角坐标系的原点，点的坐标为，点的坐标为且，满足，点在第一象限内，点从原点出发，以每秒2个单位长度的速度沿着的线路移动．
（1）点的坐标为_____；当点移动5秒时，点的坐标为______；
（2）在移动过程中，当点到轴的距离为4个单位长度时，求点移动的时间；
（3）当点在的线路移动过程中，是否存在点使的面积是20，若存在，直接写出点移动的时间；若不存在，请说明理由．
解：（1）且
，，
，，
∵四边形是长方形，
，
轴, 轴，
∴；
当点移动秒时，则移动的距离是(单位长度)，
此时点在边上，且单位长度，
∴,
故答案为：；；
（2）设点移动的时间为t秒，
∵点到轴的距离为个单位长度，
∴点在边上或边上，
当点在边上，则 ，
解得 ；
当点在边上，则，
解得 ，
综上所述，点移动的时间为秒或14秒.
（3）存在，设点移动的时间为秒，当点在边上时，如图，
, 且，，
解得 ；
当点在边上时，如图，
且，
，
解得 ；
当点在边上时，如图，
且，
，
解得 ；
综上所述，点P移动的时间 秒或 秒或秒.
24. 如图1，，，，是线段上一点，过点分别作，，分别交于点，点．

（1）求度数．
（2）点为直线上的一个动点，连接．
①如图2，当点在点的左侧，且时，判断与的位置关系，并说明理由．
②在整个运动过程中，是否存在点，使得？若存在，请求出的度数；若不存在，请说明理由．
解：（1），
，
，
．
．
，
．
．
．

（2）①．理由如下：
，
．
，．
．
．
②存在点，使得．
下分两种情况：
Ⅰ．如图，当点在点的左侧时．
，．
，．
，， ．

Ⅱ．如图，当点在点的右侧时．
，．
，．
，，．
x
16
16.1
16.2
16.3
x2
256
259.21
262.44
265.69