

河北省2024年中考真题数学试卷
展开一、选择题(本大题共16个小题,共38分.1~6小题各3分,7~16小题各2分.在每小题给出的四个选项中,只有一项是符合题目要求的)
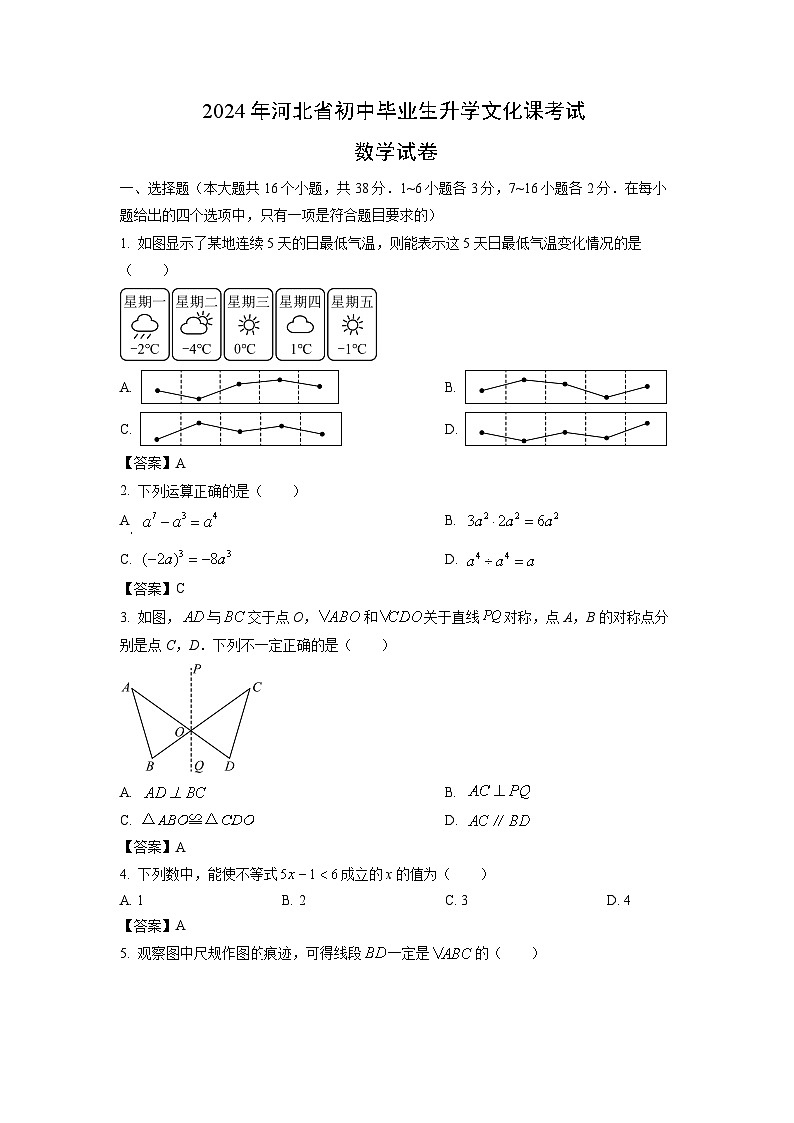
1. 如图显示了某地连续5天的日最低气温,则能表示这5天日最低气温变化情况的是( )
A. B.
C. D.
【答案】A
2. 下列运算正确的是( )
A B.
C. D.
【答案】C
3. 如图,与交于点O,和关于直线对称,点A,B的对称点分别是点C,D.下列不一定正确的是( )
A. B.
C. D.
【答案】A
4. 下列数中,能使不等式成立的x的值为( )
A. 1B. 2C. 3D. 4
【答案】A
5. 观察图中尺规作图痕迹,可得线段一定是的( )
A. 角平分线B. 高线C. 中位线D. 中线
【答案】B
6. 如图是由个大小相同的正方体搭成的几何体,它的左视图是( )
A. B.
C. D.
【答案】D
7. 节能环保已成为人们的共识.淇淇家计划购买500度电,若平均每天用电x度,则能使用y天.下列说法错误的是( )
A. 若,则B. 若,则
C. 若x减小,则y也减小D. 若x减小一半,则y增大一倍
【答案】C
8. 若a,b是正整数,且满足,则a与b的关系正确的是( )
A. B.
C. D.
【答案】A
9. 淇淇在计算正数a的平方时,误算成a与2的积,求得的答案比正确答案小1,则( )
A. 1B. C. D. 1或
【答案】C
10. 下面是嘉嘉作业本上的一道习题及解答过程:
若以上解答过程正确,①,②应分别为( )
A. ,B. ,
C. ,D. ,
【答案】D
11. 直线l与正六边形的边分别相交于点M,N,如图所示,则( )
A. B. C. D.
【答案】B
12. 在平面直角坐标系中,我们把一个点的纵坐标与横坐标的比值称为该点的“特征值”.如图,矩形位于第一象限,其四条边分别与坐标轴平行,则该矩形四个顶点中“特征值”最小的是( )
A. 点AB. 点BC. 点CD. 点D
【答案】B
13. 已知A为整式,若计算的结果为,则( )
A. xB. yC. D.
【答案】A
14. 扇文化是中华优秀传统文化的组成部分,在我国有着深厚的底蕴.如图,某折扇张开的角度为时,扇面面积为、该折扇张开的角度为时,扇面面积为,若,则与关系的图象大致是( )
A. B.
C. D.
【答案】C
15. “铺地锦”是我国古代一种乘法运算方法,可将多位数乘法运算转化为一位数乘法和简单的加法运算.淇淇受其启发,设计了如图1所示的“表格算法”,图1表示,运算结果为3036.图2表示一个三位数与一个两位数相乘,表格中部分数据被墨迹覆盖,根据图2中现有数据进行推断,正确的是( )
A. “20”左边的数是16B. “20”右边的“□”表示5
C. 运算结果小于6000D. 运算结果可以表示为
【答案】D
16. 平面直角坐标系中,我们把横、纵坐标都是整数,且横、纵坐标之和大于0的点称为“和点”.将某“和点”平移,每次平移的方向取决于该点横、纵坐标之和除以3所得的余数(当余数为0时,向右平移;当余数为1时,向上平移;当余数为2时,向左平移),每次平移1个单位长度.
若“和点”Q按上述规则连续平移16次后,到达点,则点Q的坐标为( )
A. 或B. 或
C. 或D. 或
【答案】D
二、填空题(本大题共3个小题,共10分.17小题2分,18~19小题各4分,每空2分)
17. 某校生物小组的9名同学各用100粒种子做发芽实验,几天后观察并记录种子的发芽数分别为:89,73,90,86,75,86,89,95,89,以上数据的众数为______.
【答案】89
18. 已知a,b,n均正整数.
(1)若,则______;
(2)若,则满足条件的a的个数总比b的个数少____个.
【答案】
19. 如图,的面积为,为边上的中线,点,,,是线段的五等分点,点,,是线段的四等分点,点是线段的中点.
(1)的面积为______;
(2)的面积为______.
【答案】
三、解答题(本大题共7个小题,共72分.解答应写出文字说明、证明过程或演算步骤)
20. 如图,有甲、乙两条数轴.甲数轴上的三点A,B,C所对应的数依次为,2,32,乙数轴上的三点D,E,F所对应的数依次为0,x,12.
(1)计算A,B,C三点所对应的数的和,并求的值;
(2)当点A与点D上下对齐时,点B,C恰好分别与点E,F上下对齐,求x的值.
解:(1)∵甲数轴上的三点A,B,C所对应的数依次为,2,32,
∴,,,
∴;
(2)∵点A与点D上下对齐时,点B,C恰好分别与点E,F上下对齐,
∴,∴,解得:;
21. 甲、乙、丙三张卡片正面分别写有,除正面的代数式不同外,其余均相同.
(1)将三张卡片背面向上并洗匀,从中随机抽取一张,当时,求取出的卡片上代数式的值为负数的概率;
(2)将三张卡片背面向上并洗匀,从中随机抽取一张,放回后重新洗匀,再随机抽取一张.请在表格中补全两次取出的卡片上代数式之和的所有可能结果(化为最简),并求出和为单项式的概率.
解:(1)当时,,,,
∴取出的卡片上代数式的值为负数的概率为:;
(2)补全表格如下:
∴所有等可能的结果数有种,和为单项式的结果数有种,
∴和为单项式的概率为.
22. 中国的探月工程激发了同学们对太空的兴趣.某晚,淇淇在家透过窗户的最高点P恰好看到一颗星星,此时淇淇距窗户的水平距离,仰角为;淇淇向前走了后到达点D,透过点P恰好看到月亮,仰角为,如图是示意图.已知,淇淇的眼睛与水平地面的距离,点P到的距离,的延长线交于点E.(注:图中所有点均在同一平面)
(1)求的大小及的值;
(2)求的长及的值.
解:(1)由题意可得:,,,
,,
∴,,,
∴,
∴,;
(2)∵,,
∴,
如图,过作于,
∵,设,则,
∴,
解得:,
∴,
∴.
23. 情境 图1是由正方形纸片去掉一个以中心O为顶点的等腰直角三角形后得到的.
该纸片通过裁剪,可拼接为图2所示的钻石型五边形,数据如图所示.
(说明:纸片不折叠,拼接不重叠无缝隙无剩余)
操作 嘉嘉将图1所示的纸片通过裁剪,拼成了钻石型五边形.
如图3,嘉嘉沿虚线,裁剪,将该纸片剪成①,②,③三块,再按照图4所示进行拼接.根据嘉嘉的剪拼过程,解答问题:
(1)直接写出线段的长;
(2)直接写出图3中所有与线段相等的线段,并计算的长.
探究淇淇说:将图1所示纸片沿直线裁剪,剪成两块,就可以拼成钻石型五边形.
请你按照淇淇的说法设计一种方案:在图5所示纸片的边上找一点P(可以借助刻度尺或圆规),画出裁剪线(线段)的位置,并直接写出的长.
解:如图,过作于,
结合题意可得:四边形为矩形,
∴,
由拼接可得:,
由正方形的性质可得:,
∴,,为等腰直角三角形,
∴为等腰直角三角形,
设,
∴,
∴,,
∵正方形的边长为,
∴对角线的长,
∴,
∴,
解得:,
∴;
(2)∵为等腰直角三角形,;
∴,
∴,
∵,
,
∴;
如图,以为圆心,为半径画弧交于,交于,则直线为分割线,
此时,,符合要求,
或以圆心,为半径画弧,交于,交于,则直线为分割线,
此时,,
∴,
综上:的长为或.
24. 某公司为提高员工的专业能力,定期对员工进行技能测试,考虑多种因素影响,需将测试的原始成绩x(分)换算为报告成绩y(分).已知原始成绩满分150分,报告成绩满分100分、换算规则如下:
当时,;
当时,.
(其中p是小于150的常数,是原始成绩的合格分数线,80是报告成绩的合格分数线)
公司规定报告成绩为80分及80分以上(即原始成绩为p及p以上)为合格.
(1)甲、乙的原始成绩分别为95分和130分,若,求甲、乙的报告成绩;
(2)丙、丁的报告成绩分别为92分和64分,若丙的原始成绩比丁的原始成绩高40分,请推算p的值:
(3)下表是该公司100名员工某次测试的原始成绩统计表:
①直接写出这100名员工原始成绩的中位数;
②若①中的中位数换算成报告成绩为90分,直接写出该公司此次测试的合格率.
解:(1)当时,甲的报告成绩为:分,
乙的报告成绩为:分;
(2)设丙的原始成绩为分,则丁的原始成绩为分,
①时,,,
由①②得,∴,
∴,故不成立,舍;
②时,,,
由③④得:,
∴,
∴,
∴,
∴,故不成立,舍;
③时,,
,
联立⑤⑥解得:
,且符合题意,
综上所述;
(3)①共计100名员工,且成绩已经排列好,
∴中位数是第50,51名员工成绩的平均数,
由表格得第50,51名员工成绩都是130分,
∴中位数为130;
②当时,则,解得,故不成立,舍;
当时,则,解得,符合题意,
∴ 由表格得到原始成绩为110及110以上的人数为,
∴合格率为:.
25. 已知的半径为3,弦,中,.在平面上,先将和按图1位置摆放(点B与点N重合,点A在上,点C在内),随后移动,使点B在弦上移动,点A始终在上随之移动,设.
(1)当点B与点N重合时,求劣弧的长;
(2)当时,如图2,求点B到的距离,并求此时x的值;
(3)设点O到的距离为d.
①当点A在劣弧上,且过点A的切线与垂直时,求d的值;
②直接写出d的最小值.
解:(1)如图,连接,,
∵的半径为3,,
∴,
∴为等边三角形,
∴,
∴的长为;
(2)过作于,过作于,连接,
∵,
∴,
∴四边形是矩形,
∴,,
∵,,
∴,而,
∴,
∴点B到的距离为;
∵,,
∴,
∴,
∴;
(3)①如图,∵过点A的切线与垂直,
∴过圆心,
过作于,过作于,而,
∴四边形为矩形,
∴,
∵,,
∴,
∴,
∴,
∴,即;
②如图,当为中点时,
过作于,过作于,
∴,
∴,此时最短,
如图,过作于,而,
∵为中点,则,
∴由(2)可得,
∴,
∴,
∵,
∴,
∴,
∴,
∴,
设,则,
∴,
解得:(不符合题意的根舍去),
∴的最小值为.
26. 如图,抛物线过点,顶点为Q.抛物线(其中t为常数,且),顶点为P.
(1)直接写出a的值和点Q的坐标.
(2)嘉嘉说:无论t为何值,将的顶点Q向左平移2个单位长度后一定落在上.
淇淇说:无论t为何值,总经过一个定点.
请选择其中一人的说法进行说理.
(3)当时,
①求直线PQ的解析式;
②作直线,当l与的交点到x轴的距离恰为6时,求l与x轴交点的横坐标.
(4)设与的交点A,B的横坐标分别为,且.点M在上,横坐标为.点N在上,横坐标为.若点M是到直线PQ的距离最大的点,最大距离为d,点N到直线PQ的距离恰好也为d,直接用含t和m的式子表示n.
解:(1)∵抛物线过点,顶点为Q.
∴,解得:,
∴抛物线为:,∴;
(2)把向左平移2个单位长度得到对应点的坐标为:,
当时,
∴,
∴在上,
∴嘉嘉说法正确;
∵
,
当时,,
∴过定点;
∴淇淇说法正确;
(3)①当时,
,
∴顶点,而,
设为,
∴,
解得:,
∴为;
②如图,当(等于6两直线重合不符合题意),
∴,
∴交点,交点,
由直线,设直线为,
∴,
解得:,
∴直线:,
当时,,
此时直线与轴交点的横坐标为,
同理当直线过点,
直线为:,
当时,,
此时直线与轴交点的横坐标为,
(4)如图,∵,,
∴是由通过旋转,再平移得到的,两个函数图象的形状相同,
如图,连接交于,连接,,,,
∴四边形是平行四边形,
当点M是到直线PQ的距离最大的点,最大距离为d,点N到直线PQ的距离恰好也为d,
此时与重合,与重合,
∵,,
∴的横坐标为,
∵,,
∴的横坐标为,
∴,
解得:.已知:如图,中,,平分的外角,点是的中点,连接并延长交于点,连接.
求证:四边形是平行四边形.
证明:∵,∴.
∵,,,
∴①______.
又∵,,
∴(②______).
∴.∴四边形是平行四边形.
例:“和点”按上述规则连续平移3次后,到达点,其平移过程如下:
原始成绩(分)
95
100
105
110
115
120
125
130
135
140
145
150
人数
1
2
2
5
8
10
7
16
20
15
9
5
2022年 河北省 数学 中考真题: 这是一份2022年 河北省 数学 中考真题,共2页。
2024年河北省中考数学真题: 这是一份2024年河北省中考数学真题,共4页。
模拟真题河北省中考数学模拟真题练习 卷(Ⅱ)(含详解): 这是一份模拟真题河北省中考数学模拟真题练习 卷(Ⅱ)(含详解),共27页。试卷主要包含了下列计算中,正确的是,下列式子中,与是同类项的是,已知,则的补角等于等内容,欢迎下载使用。












