浙江省宁波市鄞州区2023-2024学年八年级下学期4月期中数学试卷(解析版)

这是一份浙江省宁波市鄞州区2023-2024学年八年级下学期4月期中数学试卷(解析版)，共18页。试卷主要包含了选择题，填空题，综合题等内容，欢迎下载使用。
1. 下列各式是二次根式的是（ ）
A. B. C. D.
【答案】A
【解析】A.是二次根式，本选项符合题意；
B.不满足被开方数大于等于0，不是二次根式，本选项不符合题意；
C.字母不确定，不能保证，故不一定是二次根式，本选项不符合题意；
D.的根指数是3，故不是二次根式，本选项不符合题意，
故选：A．
2. 下列计算正确的是（ ）
A. B.
C. D.
【答案】A
【解析】；；；
故选A.
3. 下表记录了四位射击运动员选拔比赛成绩的平均数和方差：
根据表中数据，要从中选择一名成绩好且发挥稳定的运动员参加比赛，应该选择（ ）
A. 甲B. 乙C. 丙D. 丁
【答案】D
【解析】∵乙和丁的平均数较大，
∴从乙和丁中选择一人参加竞赛，
∵丁的方差较小，
∴选择丁参加比赛，
故选：D．
4. 用反证法证明“若，则”时，应假设（ ）
A. B. C. D.
【答案】A
【解析】反证法的一般步骤是先假设结论不成立，
故用反证法证明“若a>b>0，则a2>b2”的第一步是假设a2⩽b2，故选：A.
5. 若是关于的一元二次方程的一个根，则m的值为（ ）
A. 1B. 3C. D.
【答案】C
【解析】将代入方程，得：，解得：．
故选：C．
6. 一次足球联赛实行单循环比赛（每两支球队之间都比赛一场），计划安排15场比赛，设应邀请了x支球队参加联赛，则下列方程中符合题意的是（ ）
A. B.
C. D.
【答案】B
【解析】设应邀请了x支球队参加联赛，根据题意得：．故选：B
7. 如图，在平面直角坐标系中，的两条对角线，交于直角坐标系的原点，点的坐标是，则点的坐标是（ ）
A. B. C. D.
【答案】A
【解析】∵四边形ABCD是平行四边形，O为角线AC与BD的交点，
∴B与D关于原点O对称，
∵点D的坐标为（2，1），
∴点B的坐标为（-2，-1），
故选：A．
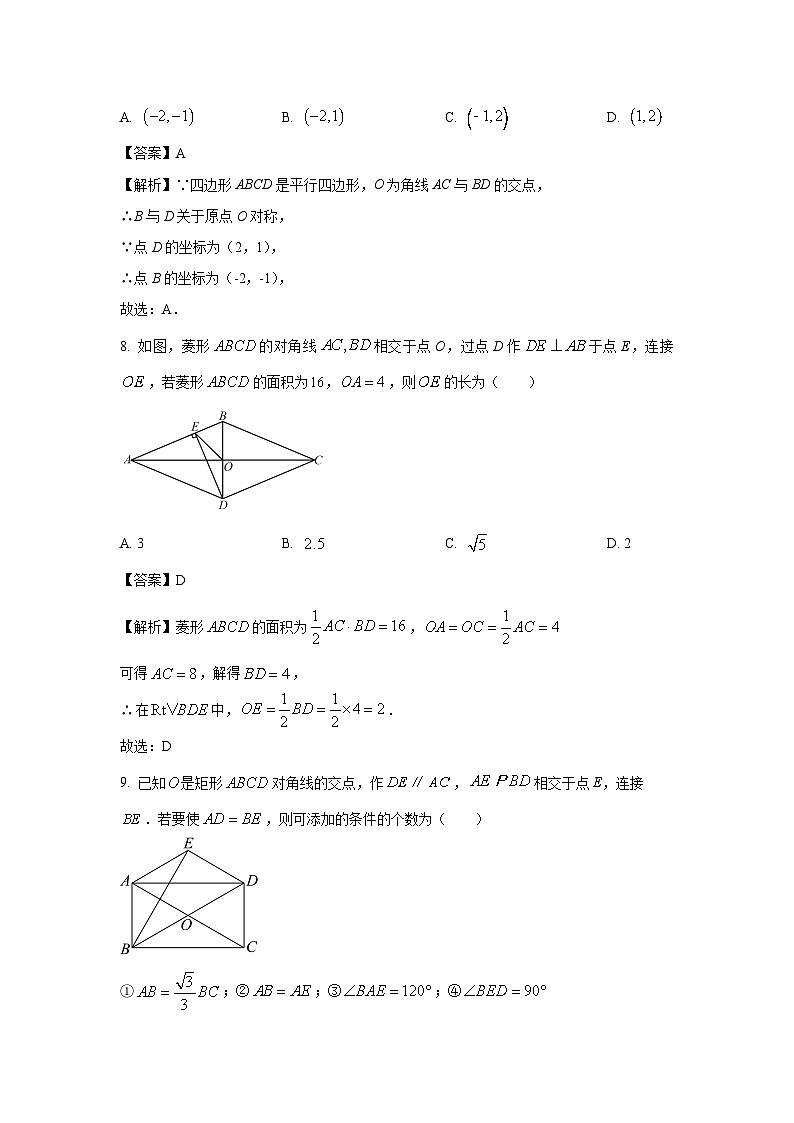
8. 如图，菱形的对角线相交于点O，过点D作于点E，连接，若菱形的面积为，，则的长为（ ）
A. 3B. C. D. 2
【答案】D
【解析】菱形的面积为，
可得，解得，
∴中，．
故选：D
9. 已知是矩形对角线的交点，作，相交于点E，连接．若要使，则可添加的条件的个数为（ ）

①；②；③；④
A. 1B. 2C. 3D. 4
【答案】D
【解析】∵四边形是矩形，
∴，
∵，，
∴四边形是平行四边形，
∵，
∴四边形是菱形，
∴，，
①当时，，，
∴，
∴是等边三角形，
∴，
∴，
∴，
∵，，
∴，
∴，故①正确，
②当时是等边三角形，同理可证；故②正确；
③当时，
∴，则等边三角形，同理可证；故③正确；
④当时，设与交于点，连，

∵，，
∴，
∵，
∴，
∴是的垂直平分线，
∴
∴,
在和中，
，
∴，
∴，故④正确；
∴可添加的条件是①②③④．故选：D．
10. 如图，边长一定的正方形ABCD，Q为CD上一个动点，AQ交BD于点M，过M作MN⊥AQ交BC于点N，作NP⊥BD于点P，连接NQ，下列结论：①AM＝MN；②MP＝BD；③BN＋DQ＝NQ；④为定值，其中正确的结论个数是（ ）
A. 1B. 2C. 3D. 4
【答案】D
【解析】如图1，连接AC、AN，AC交BD于点H，
∵四边形ABCD是正方形，
∴AC⊥BD，AC=BD，AH=CH，∠DBC＝∠ABD＝45°，
∵∠AMN＝∠ABC＝90°，∴A，B，N，M四点共圆，
∴∠NAM＝∠DBC＝45°，∠ANM＝∠ABD＝45°，
∴∠ANM＝∠NAM＝45°，∴AM＝MN，故①正确；
∵∠MAH+∠AMH=90°，∠PMN+∠AMH=90°，
∴∠HAM＝∠PMN，
∵∠AHM＝∠MPN=90°，AM＝MN，
∴Rt△AHM≌Rt△MPN（AAS），
∴MP＝AH＝AC＝BD，故②正确；
如图2，将△ADQ绕点A顺时针旋转90°至△ABR，使AD和AB重合，连接AN，
则AR=AQ，∠BAR=∠DAQ，∠ABR=∠ADQ=90°，
∴R、B、N三点在同一直线上，
∵∠BAN＋∠QAD＝∠NAQ＝45°，
∴∠RAN=∠QAN=45°，
又∵AN=AN，
∴△RAN≌△QAN（SAS），
∴RN=QN，即BN＋DQ＝NQ，故③正确；
如图3，作MS⊥AB，垂足为S，作MW⊥BC，垂足为W，
∵点M是对角线BD上的点，
∴四边形SMWB是正方形，有MS＝MW＝BS＝BW，
∵∠AMN=∠SMW=90°，
∴∠AMS=∠NMW，
又∵∠ASM=∠NWM=90°，
∴△AMS≌△NMW（ASA），∴AS＝NW，
∴AB＋BN＝SB＋BW＝2BW，
∵BW：BM＝1∶，
∴，故④正确．
故答案为D．
二、填空题
11. 一个多边形的内角和为，则这个多边形的边数是_____．
【答案】12
【解析】设这个多边形的边数为n，
根据多边形内角和定理得，
，
解得．
故答案为：12．
12. 若最简二次根式和可以合并，则的值为___________．
【答案】2
【解析】由题意得：，解得：．
所以，
∴．
故答案为2．
13. 小明用计算一组数据的方差，那么 ____．
【答案】30
【解析】由，知这10个数据的平均数为3，
所以，
故答案为：30．
14. 设、是方程的两个根，且，则________．
【答案】4
【解析】∵、是方程的两个根，
∴，，
∵，
∴，
∴．
故答案为：4．
15. 在平行四边形ABCD中，∠BAD的平分线交直线CD于点E，∠ABC的平分线交直线CD于点F，AD＝5，EF＝2，则线段AB的长为______．
【答案】8或12
【解析】∵四边形ABCD是平行四边形，
∴ BC＝AD＝5，AB＝CD，
∵AE平分∠BAD，
∴∠BAE＝∠DAE，
又∵ABCD，
∴∠EAB＝∠DEA，
∴∠DAE＝∠AED，
则AD＝DE＝5；
同理可得，CF＝CB＝5，
当点F在D、E之间时，如图1，
∵EF＝2，
∴AB＝CD＝DE+CE＝DE+（CF﹣EF）＝5+5﹣2＝8；
当点F在C、E之间时，如图2，
∵EF＝2，
∴AB＝CD＝DE+EF+CF＝5+2+5＝12．
故答案为：8或12．
16. 如图，是等边三角形，M是正方形ABCD对角线BD（不含B点）上任意一点，，（点N在AB的左侧），当AM+BM+CM的最小值为时，正方形的边长为______．
【答案】
【解析】∵为正三角形，
∴，，∴
∵BD是正方形ABCD的对角线，
∴，∴．
在和中
，
∴（SAS）
∴
在中，
又∵，
∴为等边三角形，
∴．
∵AM+BM+CM最小值为．
∴EN+MN+CM的最小值为即CE=．
过点E作交CB的延长线于F，可得．
设正方形的边长为x，则BF=，．
在，
∵，
∴
解得（负值舍去）．
∴正方形的边长为．
故答案为：．
三、综合题
17. 计算：
（1）；
（2）．
解：（1）原式；
（2），
∴，
，
∴∴，．
18. 定义：在边长为1的小正方形方格纸中，把顶点落在方格交点上的线段、三角形、四边形分别称为格点线段、格点三角形、格点四边形，在的正方形网格中，若每一个小正方形的边长均为1，请仅用无刻度直尺按要求画图．
（1）在图①中画一个以为边画一个格点正方形．
（2）在图②中画一个格点平行四边形，使平行四边形面积为6．
（3）在图③中画一个格点菱形，不是正方形（温馨提示：请画在答题卷相对应的图上）
（1）解：画一个以为边画一个格点正方形，如图所示，
（2）解：画一个格点平行四边形．如图所示，
；
（3）解：画一个格点菱形，不是正方形，如图所示，

19. 为了开展阳光体育运动，提高学生身体素质，学校开设了“引体向上”课程．为了解学生做引体向上的情况，现从八年级各班随机抽取了部分男生进行测试，绘制出不完整的统计图1和图2，请根据有关信息，解答下列问题：
（1）本次接受随机抽样调查的男生人数为 ，图1中m的值是 ；
（2）本次调查获取的样本数据（6，7，8，9，10）中，众数为 ，中位数为 ；
（3）补全条形统计图；
（4）根据样本数据，若八年级有280名男生，请你估计该校八年级男生“引体向上”次数在8次及以上的人数．
解：（1）本次接受随机抽样调查的男生人数为4÷10%＝40（人），
m%＝×100%＝15%，即m＝15，
故答案为：40，15；
（2）样本中“引体向上”次数为7次的人数为：40﹣6﹣10﹣8﹣4＝12（人），
∴众数为7次，中位数为＝8（次）．
故答案为：7，8；
（3）补全条形统计图如图：
（4）280×＝154（人），
答：估计该校八年级男生“引体向上”次数在8次及以上的人数有154人．
20. 如图，有一段15m长的旧围墙AB，现打算利用该围墙的一部分（或全部）为一边，再用32m长的篱笆围成一块长方形场地CDEF．
（1）怎样围成一个面积为126m2的长方形场地？
（2）长方形场地面积能达到130m2吗？如果能，请给出设计方案，如果不能，请说明理由．

解：（1）设CD=xm，则DE=（32﹣2x）m，
依题意得：x（32﹣2x）=126，
整理得x2﹣16x+63=0，
解得x1=9，x2=7，
当x1=9时，（32﹣2x）=14
当x2=7时,（32﹣2x）=18＞15（不合题意舍去）
∴能围成一个长14m，宽9m的长方形场地．
（2）设CD=ym，则DE=（32﹣2y）m，
依题意得y（32﹣2y）=130
整理得y2﹣16y+65=0
△=（﹣16）2﹣4×1×65=﹣4＜0
故方程没有实数根，
∴长方形场地面积不能达到130m2．
21. 如图所示，≌，点在上．
（1）求证：四边形是平行四边形；
（2）若，，求的度数．
（1）证明：，
，，，
，
，
，
四边形是平行四边形；
（2）解：由（1）知，
，
，
，
设，，
，，
，
，
，
，，
，，
．
22. 小明在学习二次根式后，发现一些含根号的式子可以写成另一个式子的平方，如：，善于思考的小明利用完全平方公式进行了以下探索：
．请你仿照小明的方法解决下列问题：
（1），则______，_______；
（2）已知x是的算术平方根，求的值；
（3）当时，化简_______．
解：（1）∵，
∴，，
故答案为：2，1；
（2）∵，x是的算术平方根，
∴，
∴
∴，整理得，
∴；
（3）∵，
∴，，
∴，
，
∴，
故答案为：．
23. 定义：对角线互相垂直的四边形叫做“垂美”四边形．
了解性质：如图1：已知四边形中，．垂足为，则有：；
性质应用：（1）如图1，四边形是垂美四边形，若，，，则 ；
性质变式：（2）如图2，图3，P是矩形所在平面内任意一点，则有以下重要结论：．请以图3为例将重要结论证明出来．
应用变式：（3）①如图4，在矩形中，O为对角线交点，P为中点，则；（写出证明过程）
②如图5，在中，，，D是内一点，且，，则最小值是 ．
（1）解：如图1，四边形是垂美四边形，
，
，，，
，
．
故答案为：；
（2）证明：过作于，交的延长线于，
由（1）性质可知：，
即：
，
又由勾股定理可知：
，
，
即；
（3）解：①设，则，
由（2）可得，
，
；
②以、为边作矩形，连接、，如图所示：
则，
由题意得：，
即，
解得：，
当、、三点共线时，最小，
的最小值的最小值；
故答案为：．
运动员
甲
乙
丙
丁
平均数（环）
方差（环）