

贵州省黔东南州榕江县乐里中学2024-2025学年 九年级上学期期中质量监测数学试卷
展开一、选择题(每小题3分,共36分.每小题均有A、B、C、D四个选项,其中只有一个选项正确)
1.下列图形中,既是轴对称图形又是中心对称图形的是( )
A.B.C.D.
2.下列方程一定属于一元二次方程的是( )
A.B.C.D.
3.平面直角坐标系内与点关于原点对称的点的坐标是( )
A.B.C.D.
4.一元二次方程的根是( )
A.B.C.,D.,
5.二次函数的顶点坐标为( )
A.B.C.D.
6.一元二次方程的根的情况是( )
A.有一个实数根B.有两个相等的实数根
C.有两个不等的实数根D.无实数根
7.将抛物线向左平移1个单位长度,再向下平移4个单位长度,得到的抛物线的解析式为( )
A.B.
C.D.
8.某品牌手机三月份销售量为400万部,四、五月份销售量连续增长,五月份销售量达到900万部,求四、五月份该品牌手机销售量的月平均增长率.设四、五月份该品牌手机销售量的月平均增长率为,根据题意可列方程为( )
A.B.
C.D.
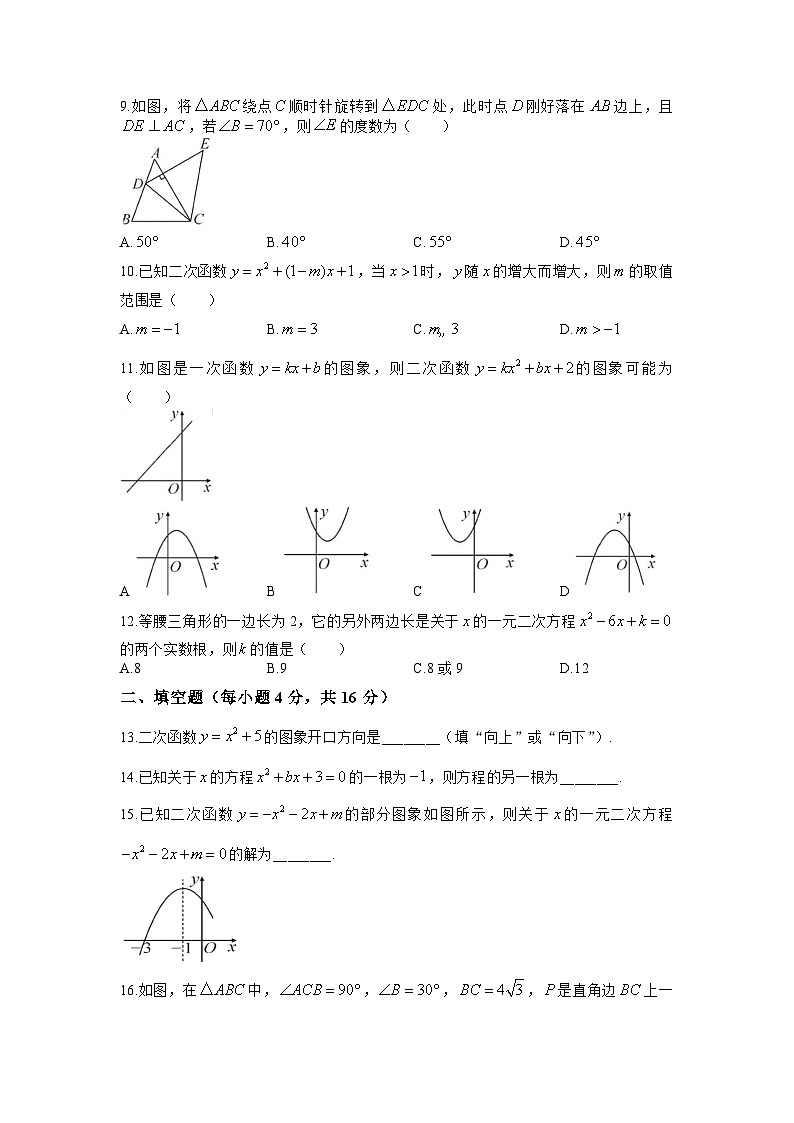
9.如图,将绕点顺时针旋转到处,此时点刚好落在边上,且,若,则的度数为( )
A.B.C.D.
10.已知二次函数,当时,随的增大而增大,则的取值范围是( )
A.B.C.D.
11.如图是一次函数的图象,则二次函数的图象可能为( )
ABCD
12.等腰三角形的一边长为2,它的另外两边长是关于的一元二次方程的两个实数根,则的值是( )
A.8B.9C.8或9D.12
二、填空题(每小题4分,共16分)
13.二次函数的图象开口方向是________(填“向上”或“向下”).
14.已知关于的方程的一根为,则方程的另一根为________.
15.已知二次函数的部分图象如图所示,则关于的一元二次方程的解为________.
16.如图,在中,,,,是直角边上一动点(点不与点,重合),连接,将线段绕点顺时针旋转得线段,连接,则线段的最小值是________.
三、解答题(本大题共9题,共98分.解答应写出必要的文字说明、证明过程或演算步骤)
17.(本题满分12分)用适当的方法解下列方程:
(1);(2).
18.(本题满分10分)如图,在平面直角坐标系中,的顶点均在格点上,已知点,.
(1)画出关于原点对称的;
(2)画出绕原点顺时针旋转后得到的,并写出点的对应点的坐标.
19.(本题满分10分)已知关于的一元二次方程.
(1)求证:无论取何值,方程总有两个不等的实数根;
(2)若方程的两个实数根为,,且,求的值.
20.(本题满分10分)如图,抛物线与直线相交于点和点.
(1)求和的值;
(2)求点的坐标,并结合图象写出不等式的解集.
21.(本题满分10分)如图,正方形的边长为2,是正方形内一点,绕点顺时针旋转到的位置,点的对应点是点,点的对应点是点.
(1)求旋转角的度数;
(2)若,,求线段的长.
22.(本题满分10分)一商店销售某种商品,平均每天可售出20件,每件盈利40元.为了扩大销售、增加盈利,该店采取了降价措施,在每件盈利不少于25元的前提下,经过一段时间销售,发现销售单价每降低1元,平均每天可多售出2件,设降价元.
(1)若降价后的销售量为件,则与之间的函数解析式为________________;(不要求写出自变量的取值范围)
(2)当每件商品降价多少元时,该商店每天销售利润为1200元?
23.(本题满分12分)小红看到一处喷水景观,喷出的水柱呈抛物线形(如图①),她对此展开研究:测得喷水头距地面,水柱在距喷水头水平距离处达到最高,最高点距地面.建立如图②所示的平面直角坐标系,并设抛物线的解析式为,其中(单位:)是水柱距喷水头的水平距离,(单位:)是水柱距地面的高度.
(1)求抛物线的解析式;
(2)小红站在水柱正下方且距喷水头水平距离处,身高的哥哥在水柱下方走动,当哥哥的头顶恰好接触到水柱时,求小红与哥哥的水平距离.
24.(本题满分12分)已知二次函数.
(1)若二次函数的图象经过点,求二次函数的解析式;
(2)在(1)的条件下,当时,求二次函数的最大值与最小值;
(3)在(1)的条件下,若点,在二次函数的图象上,且位于对称轴的两侧,当时,求的取值范围.
25.(本题满分12分)【观察猜想】
(1)如图①,在和中,,,,点在线段上,连接,,则和的数量关系是________________.
【探索证明】
(2)如图②,将绕点顺时针旋转,点落在线段上,其他条件不变,此时的度数是________,探究线段,,的关系,写出探究过程.
【拓展应用】
(3)如图③,是等腰直角三角形,,为外一点,且,连接,若,,请求出线段的长.
答案:
1.D 2.C 3.C 4.B 5.C 6.D 7.C 8.D 9.A 10.C 11.C 12.B 13.向上 14.
15., 16.2
17.解:(1),. (2),.
18.解:(1)如图,即为所求.
(2)如图,即为所求,点的坐标为.
19.(1)证明:因为,
所以无论取何值,方程总有两个不等的实数根.
(2)解:由根与系数的关系,得,.
由,得,解得.
20.解:(1)因为抛物线经过点,
所以,所以.
因为直线经过点,
所以,所以.
(2)由(1)知抛物线的解析式为,直线的解析式为.联立解得或
所以点的坐标为.
结合图象可知,不等式的解集为.
21.解:(1)由题意,得旋转角为.四边形为正方形,旋转角为.
(2)正方形的边长为2,.在中,,,..
由题意可得,.
22.(1)
(2)解:依题意,得.
整理,得.
解得,.
当时,,,符合题意.
当时,,,不符合题意,舍去.
答:当每件商品降价10元时,该商品每天销售利润为1200元.
23.解:(1)由题意知,抛物线顶点为,所以抛物线的解析式为.
将代入,得,解得.
所以抛物线的解析式为.
(2)当时,,解得,,
所以小红与哥哥的水平距离为或.
答:当哥哥的头顶恰好接触到水柱时,小红与哥哥的水平距离是或.
24.解:(1)因为二次函数的图象经过点,
所以.解得.
所以二次函数的解析式为.
(2)因为,,
所以当时,函数有最小值.
当时,函数有最大值,是,
所以当时,二次函数的最大值是5,最小值是.
(3)因为,所以二次函数的图象开口向上.
由(1)可知二次函数图象的对称轴为直线.
若点在直线的左侧,点在直线的右侧.
由题意可得
所以.
若点在直线的左侧,点在直线的右侧.
由题意可得
此不等式组无解.综上所述,的取值范围为.
25(1)
(2)解:(2).探究过程如下:
,.
又,,.
,.
,,,
,.
.
..
(3)(3)如图③,过点作,且,连接,,
,,.
.
,,.
.
,.
.易得.
贵州省黔东南州从江县宰便中学2024-2025学年七年级上学期期中质量监测数学试卷: 这是一份贵州省黔东南州从江县宰便中学2024-2025学年七年级上学期期中质量监测数学试卷,文件包含贵州省黔东南州从江县宰便中学2024-2025学年度七年级上学期期中质量监测数学试卷docx、答案docx等2份试卷配套教学资源,其中试卷共9页, 欢迎下载使用。
贵州省黔东南州从江县宰便中学2024-2025学年 九年级上学期期中质量监测数学试卷: 这是一份贵州省黔东南州从江县宰便中学2024-2025学年 九年级上学期期中质量监测数学试卷,文件包含贵州省黔东南州从江县宰便中学2024-2025学年度九年级上学期期中质量监测数学试卷docx、答案pdf等2份试卷配套教学资源,其中试卷共11页, 欢迎下载使用。
贵州省黔东南州从江县宰便中学2024-2025学年 八年级上学期期中质量监测数学试卷: 这是一份贵州省黔东南州从江县宰便中学2024-2025学年 八年级上学期期中质量监测数学试卷,文件包含贵州省黔东南州从江县宰便中学2024-2025学年度八年级上学期期中质量监测数学试卷docx、答案docx等2份试卷配套教学资源,其中试卷共10页, 欢迎下载使用。












