北师大版（2024）九年级下册第三章 圆4 圆周角和圆心角的关系同步练习题

这是一份北师大版（2024）九年级下册第三章 圆4 圆周角和圆心角的关系同步练习题，文件包含北师大版数学九下同步讲义专题12垂径定理圆周角和圆心角的关系6个知识8种题型原卷版docx、北师大版数学九下同步讲义专题12垂径定理圆周角和圆心角的关系6个知识8种题型解析版docx等2份试卷配套教学资源，其中试卷共54页， 欢迎下载使用。

倍速学习四种方法
【方法一】 脉络梳理法
知识点1.垂径定理（重点）
知识点2.垂径定理的推论（难点）
知识点3.圆周角（重点）
知识点4.圆周角定理（重点）
知识点5.圆周角定理的推论（难点）
知识点6.圆内接四边形的概念与性质（重点）
【方法二】 实例探索法
题型1.最短距离问题
题型2.辅助线的添加方法
题型3.方程思想
题型4.垂径定理的实际应用
题型5.圆中角度的计算
题型6.圆内接四边形与圆周角定理的综合应用
题型7.动点问题
题型8.圆周角定理与其他几何知识的综合
【方法三】成果评定法
【学习目标】
掌握垂径定理，并会运用垂径定理进行简单的计算。
掌握与垂径定理有关的推论，并能运用这一推论解决相关问题。
3.认识圆周角，掌握圆周角和圆心角的关系，直径所对的圆周角的特征。
4.能运用圆心角和圆周角的关系、直径所对的圆周角的特征解决相关问题。
【知识导图】
【倍速学习五种方法】
【方法一】脉络梳理法
知识点1.垂径定理（重点）
垂直于弦的直径平分这条弦，并且平分弦所对的两条弧．
【例1】．（2022秋•锡山区校级月考）如图，在⊙O中，OC⊥AB于点C，若⊙O的半径为10，AB＝16，则OC的长为 ．
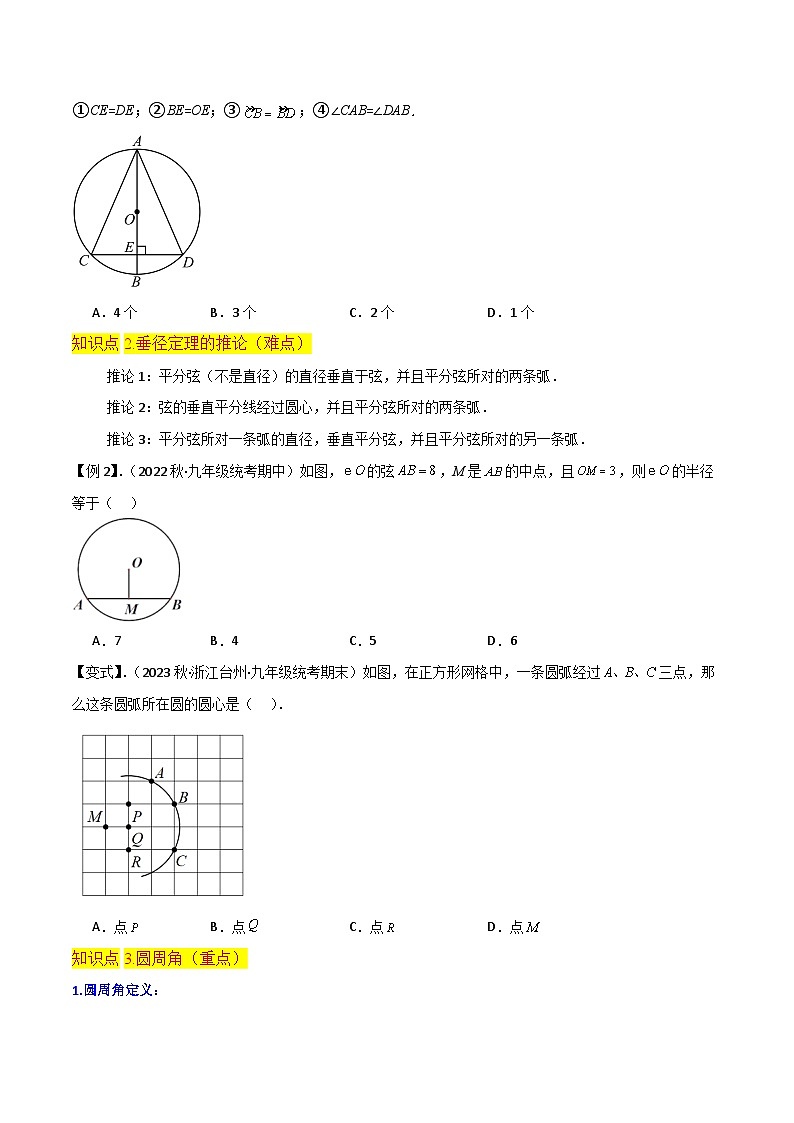
【变式】．（2022秋·江苏南京·九年级南京市第一中学校考阶段练习）如图，AB是⊙O的直径，弦CD⊥AB于点E，则下列结论一定正确的个数有（ ）
①CE=DE；②BE=OE；③；④∠CAB=∠DAB．
A．4个B．3个C．2个D．1个
知识点2.垂径定理的推论（难点）
推论1：平分弦（不是直径）的直径垂直于弦，并且平分弦所对的两条弧．
推论2：弦的垂直平分线经过圆心，并且平分弦所对的两条弧．
推论3：平分弦所对一条弧的直径，垂直平分弦，并且平分弦所对的另一条弧．
【例2】．（2022秋·九年级统考期中）如图，的弦，M是的中点，且，则的半径等于（ ）
A．7B．4C．5D．6
【变式】．（2023秋·浙江台州·九年级统考期末）如图，在正方形网格中，一条圆弧经过三点，那么这条圆弧所在圆的圆心是（ ）．
A．点B．点 C．点 D．点
知识点3.圆周角（重点）
1.圆周角定义：
像图中∠AEB、∠ADB、∠ACB这样的角，它们的顶点在圆上，并且两边都与圆相交的角叫做圆周角．

2.圆心角与圆周角的区别与联系
【例3】观察下图中角的顶点与两边有何特征? 指出哪些角是圆周角?
知识点4.圆周角定理（重点）
在同圆或等圆中，同弧或等弧所对的圆周角相等，都等于这条弧所对的圆心角的一半．
【例4】如图，，点C在上，且点C不与A、B重合，则的度数为（ ）
A． B．或 C． D． 或
【变式】如图，AB是⊙O的弦，∠AOB＝80°则弦AB所对的圆周角是 .
知识点5.圆周角定理的推论（难点）
半圆（或直径）所对的圆周角是直角，90°的圆周角所对的弦是直径．
要点诠释：
(1)圆周角必须满足两个条件：①顶点在圆上；②角的两边都和圆相交.
(2)圆周角定理成立的前提条件是在同圆或等圆中.
（3）圆心与圆周角存在三种位置关系：圆心在圆周角的一边上；圆心在圆周角的内部；圆心在圆周角的外部．（如下图）
【例5】（2023秋·江苏·九年级专题练习）如图，是的直径，A、B是上的两点，若，则的度数为（ ）

A．B．C．D．
【变式】如图，⊙A过点O(0，0)，C(，0)，D(0，1)，点B是x轴下方⊙A上的一点，连接BO、BD，则∠OBD的度数是 ．
知识点6.圆内接四边形的概念与性质（重点）
（1）定义: 圆内接四边形：顶点都在圆上的四边形，叫圆内接四边形．
（2）性质：圆内接四边形对角互补，外角等于内对角（即它的一个外角等于它相邻内角的对角）．
【例6】（2022秋•靖江市期末）如图，已知四边形ABCD内接于⊙O．求证：∠A+∠C＝180°．
【变式】如图已知四边形ABCD内接于⊙O，∠ABC＝70°，则∠ADC的度数是 ．
【方法二】实例探索法
题型1.最短距离问题
1．（2022秋·江苏无锡·九年级校考阶段练习）如图，在平面直角坐标系中，交x轴于，两点，交y轴于C，两点，点S是 上一动点，N是的中点，则线段的最小值是 ．
题型2.辅助线的添加方法
2．（2021秋·江苏·九年级专题练习）将一盛有不足半杯水的圆柱形玻璃水杯拧紧杯盖后放倒，水平放置在桌面上，水杯的底面如图所示，已知水杯内径（图中小圆的直径）是8cm，水的最大深度是2cm，则杯底有水面AB的宽度是（ ）cm.
A．6B．C．D．
题型3.方程思想
3.（2022秋•江宁区校级月考）如图是一个隧道的横截图，它的形状是以点O为圆心的一部分，如果M是⊙O中弦CD的中点，EM经过圆心O交⊙O于点E，若CD＝4m，EM＝6m，则⊙O的半径为 m．
题型4.垂径定理的实际应用
4.（2022秋•如皋市校级月考）兴隆蔬菜基地建圆弧形蔬菜大棚的剖面如图所示，已知AB＝16m，半径OA＝10m，高度CD为 m．
5.（2022•钟楼区校级模拟）筒车是我国古代发明的一种水利灌溉工具，如图1，筒车盛水桶的运行轨道是以轴心O为圆心的圆，如图2，已知圆心O在水面上方，且⊙O被水面截得弦AB长为4米，⊙O半径长为3米．若点C为运行轨道的最低点，则点C到弦AB所在直线的距离是（ ）
A．1米B．2米C．米D．米
6.（2022秋•泰州月考）如图，有一座拱桥是圆弧形，它的跨度AB＝60米，拱高PD＝18米．
（1）求圆弧所在的圆的半径r的长；
（2）当洪水泛滥到跨度只有30米时，要采取紧急措施，若拱顶离水面只有4米，即PE＝4米时，是否要采取紧急措施？
题型5.圆中角度的计算
7．（2022秋•鼓楼区期末）如图，AB为⊙O的直径，D是弦AC延长线上一点，AC＝CD，DB的延长线交⊙O于点E，连接CE．
（1）求证∠A＝∠D；
（2）若的度数为108°，求∠E的度数．
题型6.圆内接四边形与圆周角定理的综合应用
8．（2022秋•宿城区期末）如图，四边形ABCD内接于一圆，CE是边BC的延长线．
（1）求证∠DAB＝∠DCE；
（2）若∠DAB＝60°，∠ACB＝70°，求∠ABD的度数．
9．（2022秋•镇江期中）如图，四边形ABCD为⊙O的内接四边形，∠EAD＝∠BAC，BA、CD延长线交于点E．
求证：BD＝BC．
题型7.动点问题
10．（2023·江苏泰州·统考中考真题）已知：A、B为圆上两定点，点C在该圆上，为所对的圆周角．

知识回顾
(1)如图①，中，B、C位于直线异侧，．
①求的度数；
②若的半径为5，，求的长；
逆向思考
(2)如图②，P为圆内一点，且，，．求证：P为该圆的圆心；
拓展应用
(3)如图③，在（2）的条件下，若，点C在位于直线上方部分的圆弧上运动．点D在上，满足的所有点D中，必有一个点的位置始终不变．请证明．
题型8.圆周角定理与其他几何知识的综合
11．（2023•滨江区一模）如图1，AB为⊙O的直径，CD⊥AB于点E，，BF与CD交于点G．
（1）求证：CD＝BF．
（2）若BE＝1，BF＝4，求GE的长．
（3）连结GO，OF，如图2，求证：．
【方法三】 成果评定法
一．选择题（共6小题）
1．（2023秋•惠山区校级期中）如图，是的直径，弦于点，，，则的长为
A．B．C．D．
2．（2023春•鼓楼区校级月考）如图，在正方形中，，以边为直径作半圆，是半圆上的动点，于点，于点，设，，则的最小值是
A．B．C．D．
3．（2023秋•滨湖区校级期中）“圆材埋壁”是我国古代数学名著《九章算术》中的一个问题：“今有圆材，埋在壁中，不知大小，以锯锯之，深一寸，锯道长一尺．问：径几何？”用现在的几何语言表达即：如图，弦，垂足为点，寸，尺寸），则圆的直径长度是
A．12寸B．24寸C．13寸D．26寸
4．（2023秋•铜山区校级月考）如图，点、、在上，，则的度数是
A．B．C．D．
5．（2023•苏州）如图，是半圆的直径，点，在半圆上，，连接，，，过点作，交的延长线于点．设的面积为，的面积为，若，则的值为
A．B．C．D．
6．（2023秋•梁溪区校级期中）如图，是内接四边形的一个外角，若，那么的度数为
A．B．C．D．
二．填空题（共6小题）
7．（2023秋•滨海县期中）如图，点，，，在上，，，则 ．
8．（2023秋•镇江期中）如图，某圆弧形拱桥的跨度，拱高，则该拱桥的半径为 ．
9．（2023秋•高新区校级期中）如图是一个圆柱形的玻璃保温水杯，将其横放，截面是个半径为的圆，杯内水面，则水的最大深度是 ．
10．（2023秋•丰县期中）如图，点是半圆上的一个三等分点，点是的中点，是直径上一动点，的半径是2，则的最小值为 ．
11．（2023秋•鼓楼区校级月考）如图，已知的半径为7，是的弦，点在弦上．若，，则的长为 ．
12．（2023秋•建湖县期中）如图，点、、在上，，连接并延长，交于点，连接、．若，则的大小为 ．
三．解答题（共6小题）
13．（2023秋•仪征市期中）如图，在以点为圆心的两个同心圆中，大圆的弦交小圆于点、．
（1）求证；
（2）若，大圆和小圆的半径分别为6和4，则的长度是 ．
14．（2023秋•广陵区期中）如图，四边形内接于，为的直径，．
（1）若，求的度数；
（2）求证：．
15．（2023秋•句容市期中）已知：如图，，是以为直径的上的两点，分别连接、、、、，且，求证：．
16．（2023秋•淮安区期中）某地有一座圆弧形拱桥，桥下水面宽度为，拱顶高出水面（即，，
（1）求出该圆弧形拱桥所在圆的半径；
（2）现有一艘宽，船舱高出水面的货船要经过这里，此货船能顺利通过这座桥吗？
17．（2023秋•邳州市期中）“圆材埋壁”是我国古代著名数学著作《九章算术》中的一个问题：“今有圆材，埋在壁中，不知大小，以锯锯之，深一寸，锯道长一尺，问径几何？”此问题的实质是解决下面的问题：如图，为的直径，弦于点，，，求的长．
18．（2023秋•泗阳县期中）如图，是的直径，是的弦，，求的度数．