初中数学人教版（2024）七年级下册7.1.2平面直角坐标系优秀课后复习题

这是一份初中数学人教版（2024）七年级下册7.1.2平面直角坐标系优秀课后复习题，文件包含人教版数学七年级下册同步讲义+练习第七章第02讲平面直角坐标系3个知识点+5类热点题型讲练+习题巩固原卷版docx、人教版数学七年级下册同步讲义+练习第七章第02讲平面直角坐标系3个知识点+5类热点题型讲练+习题巩固解析版docx等2份试卷配套教学资源，其中试卷共28页， 欢迎下载使用。


知识点01 平面直角坐标系与点的坐标
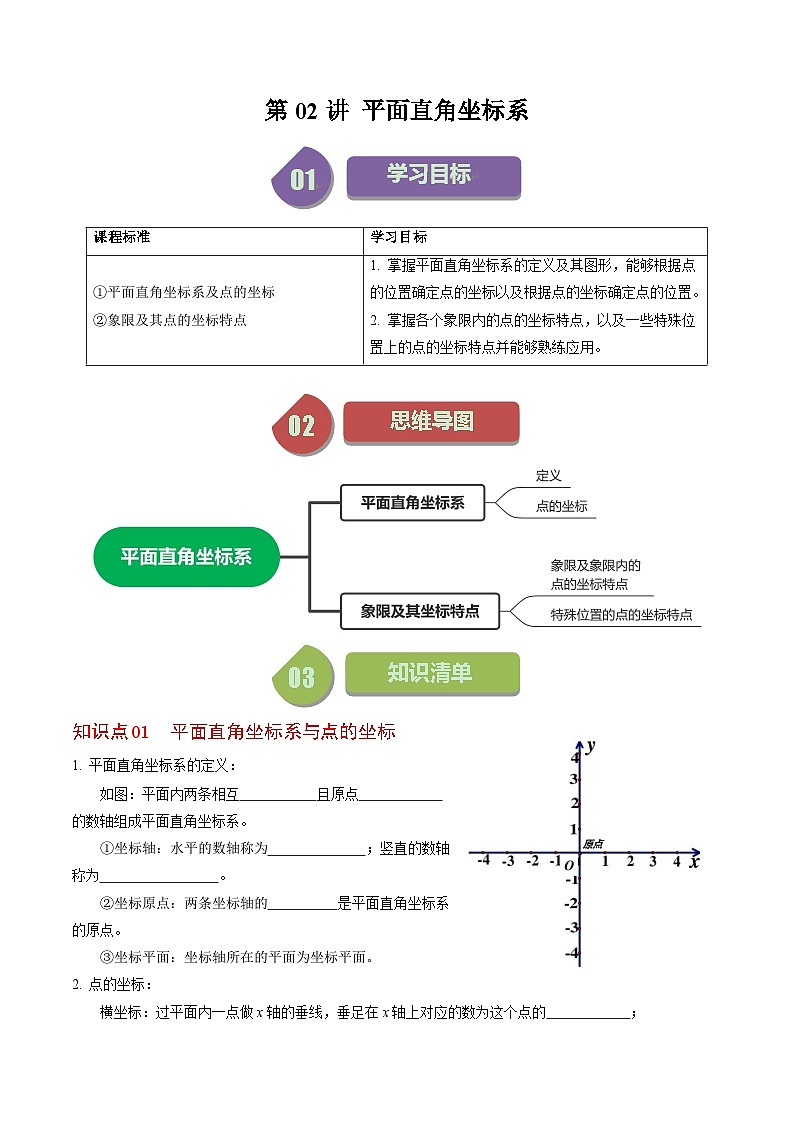
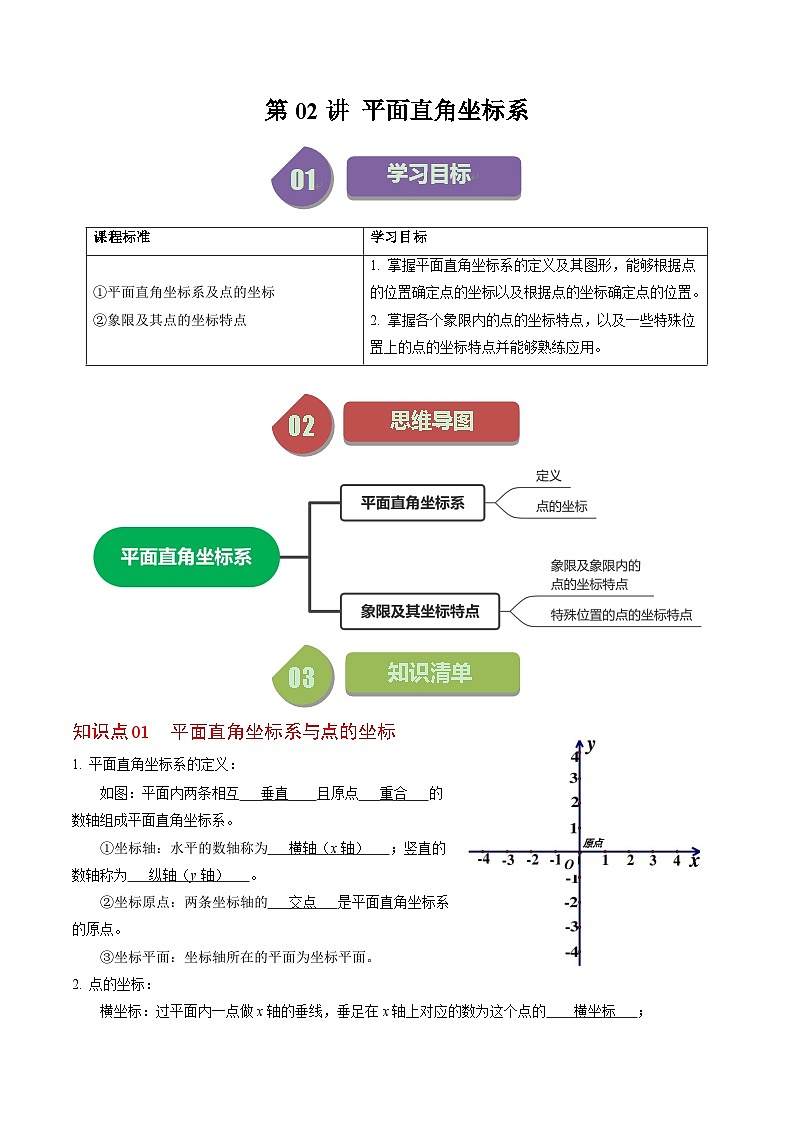
平面直角坐标系的定义：
如图：平面内两条相互 垂直 且原点 重合 的数轴组成平面直角坐标系。
①坐标轴：水平的数轴称为 横轴（x轴） ；竖直的数轴称为 纵轴（y轴） 。
②坐标原点：两条坐标轴的 交点 是平面直角坐标系的原点。
③坐标平面：坐标轴所在的平面为坐标平面。
点的坐标：
横坐标：过平面内一点做x轴的垂线，垂足在x轴上对应的数为这个点的 横坐标 ；
纵坐标：过平面内一点做y轴的垂线，垂足在y轴上对应的数为这个点的 纵坐标 ；
【即学即练1】
1．如图，写出坐标系中各点的坐标．
【解答】解：A（﹣3，1），B（0，1），C（1，﹣1），D（﹣2，0），E（2，0），F（﹣1，﹣2）．
【即学即练2】
2．在平面直角坐标系中描出下列各点：A（﹣3，2），B（﹣2，3），C（0，2），D（﹣4，0）．
【解答】解：如图所示．
知识点02 象限及象限内的坐标特点
象限：
如图，坐标轴把坐标平面分成了四个部分，每一个部分称为象限，从右上角为 第一象限 ；逆时针一次得到 第二象限 、
第三象限 以及 第四象限 。 特别地，坐标轴不属于任何一个象限。
象限内的点的坐标特点：
第一象限内的所有点的坐标，横坐标纵坐标均 大于 0；可以表示为 （+，+） 。
第二象限内的所有点的坐标，横坐标 小于 0，纵坐标, 大于 0；可以表示为 （－，+） 。
第三象限内的所有点的坐标，横坐标 小于 0，纵坐标, 小于 0；可以表示为 （－，－） 。
第四象限内的所有点的坐标，横坐标 大于 0，纵坐标, 小于 0；可以表示为 （+，－） 。
【即学即练1】
3．在平面直角坐标系中，点（4，﹣4）所在的象限是（ ）
A．第一象限B．第二象限C．第三象限D．第四象限
【解答】解：在平面直角坐标系中，点（4，﹣4）所在的象限是第四象限，
故选：D．
【即学即练2】
4．如果点A（a，b）在第二象限，则点B（b，a）在（ ）
A．第一象限B．第二象限C．第三象限D．第四象限
【解答】解：∵点A（a，b）在第二象限，
∴a＜0，b＞0，
∴点B（b，a）在第四象限．
故选：D．
知识点03 特殊位置上的点的坐标特点
坐标轴上的点的坐标特点：
①x轴上的所有点的纵坐标等于 0 ，可表示为 （x，0） 。
②y轴上的所有点的横坐标等于 0 ，可表示为 （0，y） 。
象限角平分线上的点的坐标特点：
①一、三象限的角平分线上的点的横坐标与纵坐标 相等 。
②二、四象限的角平分线上的点的横坐标与纵坐标 互为相反数 。
平行与x轴（垂直于y轴）的直线上的点的坐标特点：
平行与x轴（垂直于y轴）的直线上的所有点的坐标 纵坐标 相等。
平行与y轴（垂直于x轴）的直线上的点的坐标特点：
平行与y轴（垂直于x轴）的直线上的所有点的坐标 横坐标 相等。
点到坐标轴的距离：
点到横坐标轴的距离等于该点的 纵坐标的绝对值 。
点到纵坐标轴的距离等于该点的 横坐标的绝对值 。
【即学即练1】
5．如果点P（m+3，2m+4）在y轴上，那么点P的坐标是（ ）
A．（0，﹣2）B．（3，0）C．（1，0）D．（2，0）
【解答】解：∵点P（m+3，2m+4）在y轴上，
∴m+3＝0，
解得m＝﹣3，
∴2×m+4＝﹣6+4＝﹣2，
∴点P的坐标为（0，﹣2）．
故选：A．
【即学即练2】
6．点P（3﹣2x，5﹣x）在二、四象限的角平分线上，则x＝（ ）
A．B．2C．D．﹣2
【解答】解：∵点P（3﹣2x，5﹣x）在二、四象限的角平分线上，
∴点P的横纵坐标互为相反数，即3﹣2x＝﹣（5﹣x），
解得：．
故选：A．
【即学即练3】
7．已知点P位于y轴左侧，距y轴3个单位长度，位于x轴上方，距离x轴4个单位长度，则点P的坐标是（ ）
A．（﹣3，4）B．（3，﹣4）C．（﹣4，3）D．（4，﹣3）
【解答】解：∵P点位于y轴左侧，x轴上方，
∴P点在第二象限，
又∵P点距y轴3个单位长度，距x轴4个单位长度，
∴P点横坐标为﹣3，纵坐标为4，即点P的坐标为（﹣3，4）．
故选：A．
【即学即练4】
8．已知线段MN平行于y轴，且M（3，﹣5），N（x，2），那么x＝ 3 ．
【解答】解：∵线段MN平行于y轴，
∴M、N两点的横坐标相同，
∵两点坐标为M（3，﹣5），N（x，2），
∴x＝3．
故答案填：3．
题型01 确定点的坐标以及在平面直角坐标系中确定点的位置
【典例1】写出图中A，B，C，D，E，F，O各点的坐标．
【解答】解：A（2，3），B（3，2），C（﹣2，1），D（﹣1，﹣2），E（2.5，0），F（0，﹣2），O（0，0）．
【变式1】请在如图所示的平面直角坐标系中描出下列各点．
A（5，﹣2），B（3，0），C（2，1），D（6，3）．
【解答】解：如图所示：
【变式2】如图，在平面直角坐标系中，
（1）确定点A、B的坐标；
（2）描出点C（﹣1，﹣2），点D（2，﹣3）．
【解答】解：（1）A（﹣1，2），B（2，0）；
（2）如图所示：C，D点即为所求．
【变式3】如图，在平面直角坐标系中，
（1）写出点A，B，C，D，E的坐标；
（2）描出点P（﹣2，﹣1），Q（3，﹣2），S（2，5），T（﹣4，3），分别指出各点所在的象限．
【解答】解：（1）A（3，3），B（﹣5，2），C（﹣4，﹣3），D（4，﹣3），E（5，0）；
（2）如图所示：
点P在第三象限，点Q在第四象限，点S在第一象限，点T在第二象限．
题型02 判定点所在的象限
【典例1】在平面直角坐标系中，点P（﹣2，3）在（ ）
A．第一象限B．第二象限C．第三象限D．第四象限
【解答】解：因为点P（﹣2，3）的横坐标小于0，纵坐标大于0，
所以点P（﹣2，3）在第二象限．
故选：B．
【变式1】平面直角坐标系中，（m2+1，﹣2）在第 四 象限．
【解答】解：∵该点的横坐标m2+1＞0，纵坐标﹣2＜0，
∴该点位于第四象限．
故答案为：四．
【变式2】若点P（﹣3，a）在x轴上，则点Q（a﹣3，a+1）所在象限是（ ）
A．第一象限B．第二象限C．第三象限D．第四象限
【解答】解：由题意得：a＝0，
∴a﹣3＝﹣3，a+1＝1，
∴Q（﹣3，1）在第二象限，
故选：B．
【变式3】若点P（a，b）在第二象限，则M（ab，﹣a）应在（ ）
A．第一象限B．第二象限C．第三象限D．第四象限
【解答】解：∵点P（a，b）在第二象限，
∴a＜0，b＞0，
∴ab＜0，﹣a＞0，
∴点M（ab，﹣a）在第二象限．
故选：B．
【变式4】若a＜0，b＞0，则点（a，b+1）在（ ）
A．第一象限B．第二象限C．第三象限D．第四象限
【解答】解：∵a＜0，b＞0，
∴b+1＞0，
点（a，b+1）在第二象限．
故选：B．
题型03 根据点所在的位置的特点求值
【典例1】在平面直角坐标系中，点M（m﹣3，m+1）在x轴上，则点M的坐标为（ ）
A．（﹣4，0）B．（0，﹣2）C．（﹣2，0）D．（0，﹣4）
【解答】解：∵点M（m﹣3，m+1）在平面直角坐标系的x轴上，
∴m+1＝0，
解得m＝﹣1，
∴m﹣3＝﹣1﹣3＝﹣4，
点M的坐标为（﹣4，0）．
故选：A．
【变式1】已知点A（m﹣1，m+4）在y轴上，则m的值为（ ）
A．﹣4B．﹣1C．1D．4
【解答】解：∵点A（m﹣1，m+4）在y轴上，
∴m﹣1＝0，
解得m＝1．
故选：C．
【变式2】已知点P（5a+1，6a+2）在一、三象限的角平分线上，则a＝ ﹣1 ．
【解答】解：∵点P（5a+1，6a+2）在一、三象限的角平分线上，
∴5a+1＝6a+2，
解得a＝﹣1．
故答案为：﹣1．
【变式3】若点M（5+a，a﹣3）在第二、四象限角平分线上，则a的值是（ ）
A．1B．2C．﹣1D．﹣2
【解答】解：∵点M（5+a，a﹣3）在第二、四象限角平分线上，
∴5+a+a﹣3＝0，
∴a＝﹣1，
故选：C．
【变式4】在平面直角坐标系中，点P（a，b）在第一象限的角平分线上，且a、b满足2a+b＝9，则点P的坐标为（ ）
A．（1，7）B．（2，2）C．（3，3）D．（9，﹣9）
【解答】解：∵点P（a，b）在第一象限的角平分线上，
∴a＝b，
∵2a+b＝9，
∴2a+a＝9，
∴a＝3，
∴符合要求的坐标为（3，3）．
故选：C．
【变式5】已知点P、Q的坐标分别为（2m﹣5，m﹣1）、（n+2，2n﹣1），若点P在第二、四象限的角平分线上，点Q在第一、三象限的角平分线上，则mn的值为 8 ．
【解答】解：∵点P（2m﹣5，m﹣1）在第二、四象限的角平分线上，
∴2m﹣5+m﹣1＝0．
解得：m＝2．
∵点Q（n+2，2n﹣1）在第一、三象限的角平分线上，
∴n+2＝2n﹣1．
解得：n＝3．
∴mn＝23＝8．
故答案为：8．
题型04 根据点到坐标轴的距离求坐标
【典例1】第三象限内的点P到x轴的距离是7，到y轴的距离是8，那么点P的坐标是（ ）
A．（﹣8，﹣7）B．（﹣7，﹣8）C．（8，7）D．（7，8）
【解答】解：∵第三象限的点P到x轴的距离是7，到y轴的距离是8，
∴点P的横坐标是﹣8，纵坐标是﹣7，
∴点P的坐标为（﹣8，﹣7）．
故选：A．
【变式1】点M在第二象限，距离x轴5个单位长度，距离y轴3个单位长度，则M点的坐标为（ ）
A．（5，﹣3）B．（﹣5，3）C．（3，﹣5）D．（﹣3，5）
【解答】解：∵点P位于第二象限，
∴点的横坐标为负数，纵坐标为正数，
∵点距离x轴5个单位长度，距离y轴3个单位长度，
∴点的坐标为（﹣3，5）．
故选：D．
【变式2】在平面直角坐标系内有一点A到x轴的距离是2，到y轴距离是4，且A点在第四象限内，则点A的坐标是（ ）
A．（4，﹣2）B．（﹣4，﹣2）C．（﹣2，4）D．（﹣4，2）
【解答】解：∵点A到x轴的距离是2，到y轴距离是4，且A点在第四象限内，
∴点A的坐标是（4，﹣2）．
故选：A．
题型05 根据平行与坐标轴的直线的坐标特点求坐标
【典例1】在平面直角坐标系中，P（1，2），点Q在x轴下方，PQ∥y轴，若PQ＝5，则点Q的坐标为（ ）
A．（﹣4，2）B．（6，2）C．（1，﹣3）D．（1，7）
【解答】解：∵点Q在x轴下方，PQ∥y轴，
∴设点Q（1，y），y＜0．
又∵PQ＝5，
∴2﹣y＝5，解得y＝﹣3．
∴点Q的坐标为（1，﹣3）．
故选：C．
【变式1】已知点A的坐标为（﹣1，3），线段AB平行于x轴且AB＝5，则点B的坐标为（ ）
A．（4，3）B．（4，3）或（﹣6，3）
C．（﹣1，8）D．（﹣1，8）或（1，﹣2）
【解答】解：由题知，
因为线段AB平行于x轴，
所以线段AB上所有点的纵坐标相等．
又因为点A坐标为（﹣1，3），且AB＝5，
所以点B的坐标为（﹣6，3）或（4，3）．
故答案为：B．
【变式2】在平面直角坐标系中，已知点A（m﹣1，2m﹣2），B（﹣3，2）．若直线AB∥y轴，则线段AB的长为（ ）
A．2B．4C．6D．8
【解答】解：∵AB∥y轴，
∴点A和点B的横坐标相同，
∴m﹣1＝﹣3，
∴m＝﹣2，
∴2m﹣2＝﹣6，
∴点A的坐标为（﹣3，﹣6），
∵点B的坐标为（﹣3，2）且AB∥y轴，
∴AB＝2﹣（﹣6）＝8，
故选：D．
【变式3】在平面直角坐标系中，若A（m+3，﹣1），B（1﹣m，3），且直线AB∥y轴，则m的值是（ ）
A．﹣1B．1C．2D．3
【解答】解：∵直线AB∥y轴，
∴m+3＝1﹣m，
∴m＝﹣1．
故答案为：A．
1．在平面直角坐标系中，下列各选项的点在第二象限的是（ ）
A．（1，2）B．（﹣3，2）C．（0，0）D．（2，﹣3）
【解答】解：A、（1，2）在第一象限，故A不符合题意；
B、（﹣3，2）在第二象限，故B符合题意；
C、（0，0）在坐标轴上，故C不符合题意；
D、（2，﹣3）在第四象限，故D不符合题意；
故选：B．
2．若点P（m，n）在第二象限，且到x轴的距离为2，到y轴的距离为3，则点P的坐标是（ ）
A．（﹣2，3）B．（2，﹣3）C．（﹣3，2）D．（3，﹣2）
【解答】解：∵点P到x轴的距离为2，到y轴的距离为3，
∴点P的纵坐标的绝对值是2，横坐标的绝对值是3，
∵点P在第二象限，
∴点P的横坐标为负，纵坐标为正．
∴点P的坐标为（﹣3，2）．
故选：C．
3．在平面直角坐标系中，点P（m，n）位于第四象限，下列结论一定正确的是（ ）
A．mn＞0B．mn＜0C．m+n＞0D．m+n＜0
【解答】解：∵点P（m，n）位于第四象限，
∴m＞0，n＜0，
∴mn＜0，
故选：B．
4．在平面直角坐标系中，点P（﹣1﹣m2，1）位于（ ）
A．第一象限B．第二象限C．第三象限D．第四象限
【解答】解：∵m2≥0，
∴﹣1﹣m2＜0，
∴点P在第二象限，
故选：B．
5．若点P（a﹣3，2﹣a）在y轴上，则点P的坐标为（ ）
A．（0，1）B．（0，﹣1）C．（1，0）D．（﹣1，0）
【解答】解：由点P（a﹣3，2﹣a）在y轴上可得：
a﹣3＝0．
解得a＝3，
2﹣a＝﹣1，
点P的坐标为（0，﹣1）．
故选：B．
6．已知点P（x，y）在x轴的上方，且|x|＝3，y2＝4，则点P的坐标为（ ）
A．（3，2）B．（3，﹣2）
C．（﹣3，2）D．（3，2）或（﹣3，2）
【解答】解：∵|x|＝3，y2＝4，
∴x＝±3，y＝±2，
又∵点P（x，y）在x轴的上方，
∴y＞0，
∴y＝2，
∴点P的坐标为（3，2）或（﹣3，2），
故选：D．
7．小美家（A）、小明家（B）、小丽家（C）在同一个小区，位置如图所示，如果小美家（A）的位置用（﹣4，﹣3）表示，小明家（B）的位置用（2，1）表示，那么小丽家（C）的位置可以表示为（ ）
A．（0，﹣2）B．（﹣2，0）C．（﹣2，1）D．（﹣1，2）
【解答】解：如图，建立坐标系如下：
∴C（﹣2，0），
故选：B．
8．下列说法不正确的是（ ）
A．若x+y＝0，则点P（x，y）一定在第二、第四象限角平分线上
B．点P（﹣2，3）到y轴的距离为2
C．若P（x，y）中xy＝0，则P点在x轴上
D．点A（﹣a2﹣1，|b|+1）一定在第二象限
【解答】解：A、若x+y＝0，则x、y互为相反数，点P（x，y）一定在第二、四象限角平分线上，原说法正确，故此选项不符合题意；
B、点P（﹣2，3）到y轴的距离是2，原说法正确，故此选项不符合题意；
C、若P（x，y）中xy＝0，则P点在x轴或y轴上，原说法不正确，故此选项符合题意；
D、因为﹣a2﹣1＜0，|b|+1＞0，所以点A（﹣a2﹣1，|b|+1）一定在第二象限，原说法正确，故此选项不符合题意．
故选：C．
9．在平面直角坐标系中，若A（m+3，﹣1），B（3，1﹣m），且直线AB∥y轴，则m的值是（ ）
A．0B．1C．2D．3
【解答】解：∵直线AB∥y轴，
∴m+3＝3，
∴m＝0．
故选：A．
10．已知点P的坐标为（a，b），其中a，b均为实数，若a，b满足3a＝2b+5，则称点P为“和谐点”．若点M（m﹣1，3m+2）是“和谐点”，则点M所在的象限是（ ）
A．第四象限B．第三象限C．第二象限D．第一象限
【解答】解：点M在第三象限，
理由如下：
∵点M（m﹣1，3m+2）是“和谐点”，
∴3（m﹣1）＝2（3m+2）+5，
解得m＝﹣4，
∴m﹣1＝﹣5，3m+2＝﹣10，
∴点M在第三象限．
故选：B．
11．已知点P（a，2a﹣1）在一、三象限的角平分线上，则a的值为 1 ．
【解答】解：由题意知a＝2a﹣1，
解得a＝1，
故答案为：1．
12．已知点P（a2﹣9，a﹣1）在x轴上，则点P的坐标为 （﹣8，0） ．
【解答】解：∵点P（a2﹣9，a﹣1）在x轴上，
∴a﹣1＝0，
∴a＝1，
∴a2﹣9＝12﹣9＝1﹣9＝﹣8，
∴点P的坐标为（﹣8，0），
故答案为：（﹣8，0）．
13．已知点P（a，2a+3）在第二象限，且P到x轴的距离与它到y轴的距离相等，则a＝ ﹣1 ．
【解答】解：∵点P（a，2a+3）在第二象限，
∴a＜0，2a+3＞0，
∵P到x轴的距离与它到y轴的距离相等，
∴﹣a＝2a+3，
解得a＝﹣1．
故答案为：﹣1．
14．在平面直角坐标系中，点C（2，1），CD＝5，CD平行于y轴，则点D坐标为 （2，6）或（2，﹣4） ．
【解答】解：1+5＝6，1﹣5＝﹣4，
∴点D的坐标为（2，6）或（2，﹣4），
故答案为：（2，6）或（2，﹣4）．
15．如图，点A（1，0）第一次跳动至点A1（﹣1，1），第二次跳动至点A2（2，1），第三次跳动至点A3（﹣2，2），第四次跳动至点A4（3，2），…，依此规律跳动下去，点A第2024次跳动至点A2024的坐标是 （1013，1012） ．
【解答】解：由题知，
因为点A的坐标为（1，0），
根据点A的运动方式可知，
点A1的坐标为（﹣1，1）；
点A2的坐标为（2，1）；
点A3的坐标为（﹣2，2）；
点A4的坐标为（3，2）；
点A5的坐标为（﹣3，3）；
点A6的坐标为（4，3）；
…，
由此可见，点An的坐标为（）（n为正偶数），
当n＝2024时，
，
＝1012，
即点A2024的坐标为（1013，1012）．
故答案为：（1013，1012）．
16．已知点P（m﹣3，2m+4），根据下列条件求点P的坐标．
（1）点P在x轴上；
（2）点P在y轴上．
【解答】解：（1）∵点P在x轴上，
∴2m+4＝0，
解得：m＝﹣2，
∴m﹣3＝﹣2﹣3＝﹣5，
∴点P的坐标为（﹣5，0）；
（2）∵点P在y轴上，
∴m﹣3＝0，
解得：m＝3，
∴2m+4＝6+4＝10，
∴点P的坐标为（0，10）．
17．在平面直角坐标系中，已知点M（2﹣m，1+2m）．
（1）若点M在y轴上，求M点的坐标；
（2）若点M在第二、四象限的角平分线上，求M点的坐标．
【解答】解：（1）由题意得：2﹣m＝0，
∴m＝2，
∴1+2m＝1+4＝5，
∴M（0，5）；
（2）∵M在第二、四象限的角平分线上，
∴2﹣m+1+2m＝0，
∴m＝﹣3，
∴M（5，﹣5）．
18．已知点P（2a﹣2，a+5），解答下列各题：
（1）若点P在x轴上．求出点P的坐标；
（2）若点Q的坐标为（4，5），直线PQ∥x轴，求出点P的坐标；
（3）若点P到x轴、y轴的距离相等，求出点P的坐标，并说出P点所在的象限．
【解答】解：（1）∵点P在x轴上，
∴a+5＝0，
∴a＝﹣5，
∴2a﹣2＝2×（﹣5）﹣2＝﹣12，
∴点P的坐标为（﹣12，0）；
（2）点Q的坐标为（4，5），直线PQ∥x轴，
∴a+5＝5，
∴a＝0，
∴2a﹣2＝﹣2，
∴点P的坐标为（﹣2，5）；
（3）∵点P到x轴、y轴的距离相等，
∴|2a﹣2|＝|a+5|，
∴a＝﹣1或7，
点P的坐标为（﹣4，4）或（12，12）．
19．已知当m，n都是实数，且满足2m＝8+n时，称p（m﹣1，）为“开心点”．例如点A（5，3）为“开心点”．
∵当A（5，3）时，m﹣1＝5，＝3，得m＝6，n＝4，
∴2m＝2×6＝12，8+n＝8+4＝12．
∴2m＝8+n．∴A（5，3）是“开心点”．
（1）判断点B（9，6）是否为“开心点”，并说明理由；
（2）若点M（a，2a﹣3）是“开心点”，请判断点M在第几象限？并说明理由．
【解答】解：（1）点B（9，6）不是“开心点”，理由如下：
∵当点B（9，6）时，m﹣1＝9，＝6，
解得：m＝10，n＝10，
∵2m＝20，8+n＝18，
∴2m≠8+n，
∴点B（9，6）不是“开心点”；
（2）∵点M（a，2a﹣3）是“开心点”，
∴m﹣1＝a，＝2a﹣3，
解得：m＝a+1，n＝4a﹣8，
∵2m＝8+n，
∴2（a+1）＝8+4a﹣8，
解得：a＝1，
∴2a﹣3＝﹣1，
此时点M的坐标为（1，﹣1），
∴点M在第四象限．
20．在平面直角坐标系中，对于点A（x，y），若点B的坐标为（x+ay，ax+y），其中a为常数，则称点B是点A的“a倍相关点”．
例如，点A（1，3）的“2倍相关点”B的横坐标为：1+2×3＝7，纵坐标为：2×1+3＝5，所以点A的“2倍相关点”B的坐标为（7，5）．
（1）已知点P（﹣2，3）的“倍相关点”是点Q（s，t），求s+t的值；
（2）已知点M（1，2m）的“﹣2倍相关点”是点N，且点N在y轴上，求点N到x轴的距离．
【解答】解：（1）根据题意，得s＝﹣2+×3＝﹣1，t＝×（﹣2）+3＝，
∴s+t＝﹣1+＝；
（2）设点N的坐标为（p，q），则p＝1﹣4m，q＝﹣2+2m，
∴点N的坐标为（1﹣4m，﹣2+2m），
∵点N在y轴上，
∴1﹣4m＝0，解得m＝，
∴点N的坐标为（0，﹣），
∴点N到x轴的距离为|﹣|＝．
课程标准
学习目标
①平面直角坐标系及点的坐标
②象限及其点的坐标特点
掌握平面直角坐标系的定义及其图形，能够根据点的位置确定点的坐标以及根据点的坐标确定点的位置。
掌握各个象限内的点的坐标特点，以及一些特殊位置上的点的坐标特点并能够熟练应用。