

江苏淮安市凌桥中学2024-2025学年九上数学第7周阶段性训练模拟练习【含答案】
展开A.28°B.30°C.31°D.36°
2.随着全球能源危机的逐渐加重,太阳能发电行业发展迅速.全球太阳能光伏应用市场持续稳步增长,2020年全球装机总量约600GW,预计到2022年全球装机总量达到864GW.设全球新增装机量的年平均增长率为x,则可列的方程为( )
A.600(1+2x)=864B.600+2x=864
C.(600+x)2=864D.600(1+x)2=864
3.某超市一月份的营业额为200万元,第一季度的营业额共1000万元,如果平均每月增长率为x,则由题意列方程应为( )
A.200(1+x)2=1000
B.200+200⋅2⋅x=1000
C.200+200⋅3⋅x=1000
D.200[1+(1+x)+(1+x)2]=1000
4.如图,⊙M的半径为4,圆心M的坐标为(6,8),P是⊙M上的任意一点,PA⊥PB,且PA、PB与x轴分别交于A、B两点.若点A、B关于原点O对称,则AB长的最小值为( )
A.6B.8C.12D.16
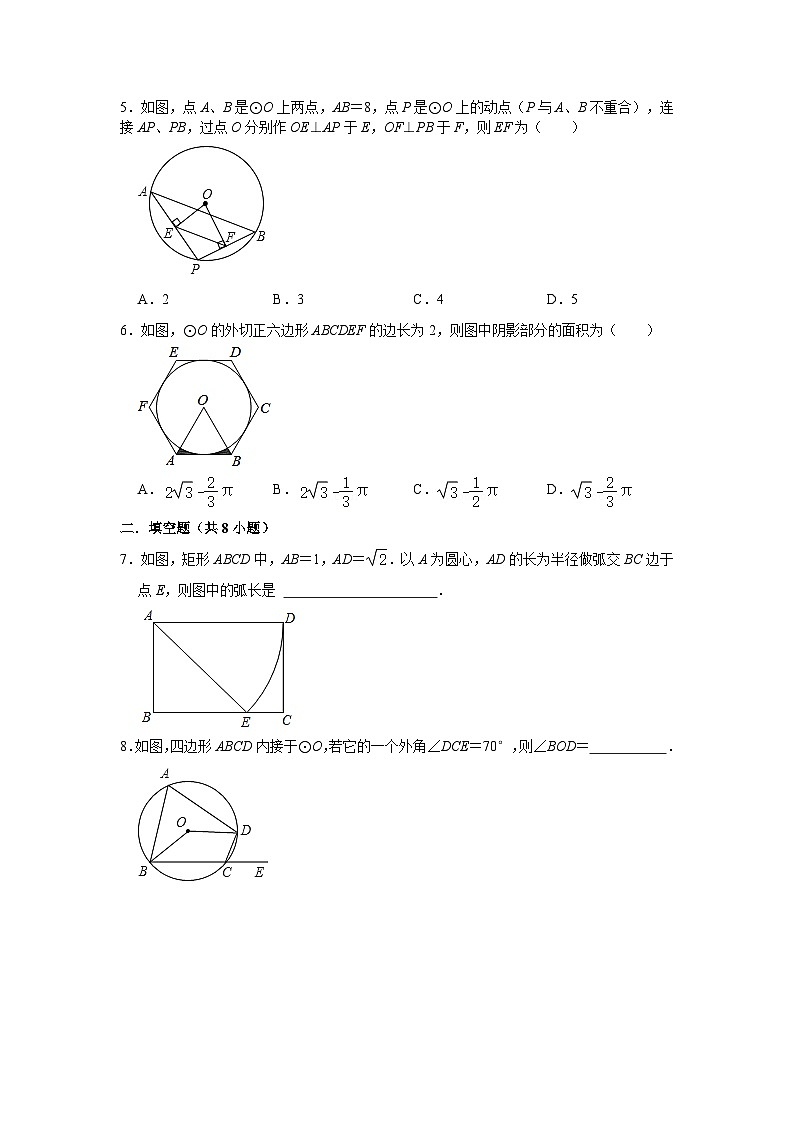
5.如图,点A、B是⊙O上两点,AB=8,点P是⊙O上的动点(P与A、B不重合),连接AP、PB,过点O分别作OE⊥AP于E,OF⊥PB于F,则EF为( )
A.2B.3C.4D.5
6.如图,⊙O的外切正六边形ABCDEF的边长为2,则图中阴影部分的面积为( )
A.B.C.D.
二.填空题(共8小题)
7.如图,矩形ABCD中,AB=1,AD=.以A为圆心,AD的长为半径做弧交BC边于点E,则图中的弧长是 .
8.如图,四边形ABCD内接于⊙O,若它的一个外角∠DCE=70°,则∠BOD= .
9.如图,在Rt△AOB中,OA=OB=3,⊙O的半径为1,点P是AB边上的动点,过点P作⊙O的一条切线PQ(点Q为切点),则切线PQ的最小值为 .
10.如图,AB是⊙O的直径,弦CD⊥AB于点E.若AB=10,AE=1,则弦CD的长是 .
11.若m是方程2x2﹣3x﹣1=0的一个根,则4m2﹣6m+2019的值为 .
12.在实数范围内定义运算“☆”和“★”,其规则为:a☆b=a2+b2,a★b=,则方程3☆x=x★12的解为 .
13.如图,某小区有一块长为30m,宽为24m的矩形空地,计划在其中修建两块相同的矩形绿地,它们的面积之和为480m2,两块绿地之间及周边有宽度相等的人行通道,则人行通道的宽度为 m.
14.如图,在扇形OAB中,∠AOB=110°,将扇形OAB沿过点B的直线折叠,点O恰好落在弧AB上的点D处,折痕交OA于点C,则弧AD的度数为 .
三.解答题(共8小题)
15.商店销售某种商品,平均每天可售出20件,每件盈利40元.为了扩大销售,增加盈利,该店采取了降价措施,在每件盈利不少于25元的前提下,经过一段时间销售,发现销售单价每降低1元,平均每天可多售出2件.
(1)若降价2元,则平均每天销售数量为 件;
(2)当每件商品降价多少元时,该商店每天销售利润为1050元?
16.如图,AB为⊙O的直径,PQ切⊙O于E,AC⊥PQ于C,交⊙O于D.
(1)求证:AE平分∠BAC;
(2)若AD=EC=4,求⊙O的半径.
17.某商店购进一批成本为每件30元的商品,经调查发现,该商品每天的销售量y(件)与销售单价x(元)之间满足一次函数关系,其图象如图所示.
(1)求该商品每天的销售量y与销售单价x之间的函数关系式;
(2)若商店按销售单价不低于成本价,且不高于60元的价格销售,要使销售该商品每天获得的利润为800元,求每天的销售量应为多少件?
18.如图①,②,在平面直角坐标系xOy中,点A的坐标为(4,0),以点A为圆心,4为半径的圆与x轴交于O,B两点,OC为弦,∠AOC=60°,P是x轴上的一动点,连接CP.
(1)求∠OAC的度数;
(2)如图①,当CP与⊙A相切时,求PO的长;
(3)如图②,当点P在直径OB上时,CP的延长线与⊙A相交于点Q,问PO为何值时,△OCQ是等腰三角形?
19.一商店销售某种商品,平均每天可售出20件,每件盈利40元.为了扩大销售、增加盈利,该店采取了降价措施,在每件盈利不少于25元的前提下,经过一段时间销售,发现销售单价每降低1元,平均每天可多售出2件.
(1)若降价4元,则平均每天销售数量为 件;
(2)当每件商品降价多少元时,该商店每天销售利润为1200元?
20.阅读下面的材料,回答问题:
解方程x4﹣5x2+4=0,这是一个一元四次方程,根据该方程的特点,它的解法通常是:
设x2=y,那么x4=y2,于是原方程可变为y2﹣5y+4=0①,解得y1=1,y2=4.
当y=1时,x2=1,∴x=±1;当y=4时,x2=4,∴x=±2;
∴原方程有四个根:x1=1,x2=﹣1,x3=2,x4=﹣2.
仿照上面方法,解方程:(x2+3x)2+4(x2+3x)+3=0.
21.如图,在平面直角坐标系中,⊙A的半径为1,圆心A点的坐标为(,0),直线OB是一次函数y=x的图象,让⊙A沿x轴负方向以每秒1个单位长度移动,移动时间为t秒.
(1)直线OB与x轴所夹的锐角度数为 °;
(2)求出运动过程中⊙A与直线OB相切时的t的值;
(3)运动过程中,当⊙A与直线OB相交所得的弦长为1时,直接写出t= .
22.在长方形ABCD中,AB=5cm,BC=6cm,点P从点A开始沿边AB向终点B以1cm/s的速度移动,与此同时,点Q从点B开始沿边BC向终点C以2cm/s的速度移动.如果P、Q分别从A、B同时出发,当点Q运动到点C时,两点停止运动.设运动时间为t秒.
(1)填空:BQ= ,PB= (用含t的代数式表示);
(2)当t为何值时,PQ的长度等于5cm?
(3)是否存在t的值,使得五边形APQCD的面积等于26cm2?若存在,请求出此时t的值;若不存在,请说明理由.
参考答案与试题解析
一.选择题(共6小题)
1.【解答】解:∵AB是⊙O的切线,A为切点,
∴OA⊥AB,
∴∠OAB=90°,
∴∠AOB=90°﹣∠B=90°﹣28°=62°,
∴∠D=∠AOC=×62°=31°.
故选:C.
2.【解答】解:设全球新增装机量的年平均增长率为x,
由题意得:600(1+x)2=864,
故选:D.
3.【解答】解:设平均每月增长率为x,则二月份的营业额为200(1+x)万元,三月份的营业额为200(1+x)2万元,
根据题意得:200[1+(1+x)+(1+x)2]=1000.
故选:D.
4.【解答】解:连接OP,
∵PA⊥PB,
∴∠APB=90°,
∵AO=BO,
∴AB=2PO,
若要使AB取得最小值,则PO需取得最小值,
连接OM,交⊙M于点P′,当点P位于P′位置时,OP′取得最小值,过点M作MQ⊥x轴于点Q,
则OQ=6,MQ=8,
∴OM=10,
又∵MP′=4,
∴OP′=6,
∴AB=2OP′=12,
故选:C.
5.【解答】解:∵OE⊥AP于E,OF⊥PB于F,AB=8,
∴AE=PE,PF=BF,
∴EF是△APB的中位线,
∴EF=AB=×8=4.
故选:C.
6.【解答】解:∵六边形ABCDEF是正六边形,
∴∠AOB=60°,
∴△OAB是等边三角形,OA=OB=AB=2,
设点G为AB与⊙O的切点,连接OG,则OG⊥AB,
∴OG=OA•sin60°=2×=,
∴S阴影=S△OAB﹣S扇形OMN=×2×﹣=﹣π.
故选:C.
二.填空题(共8小题)
7.【解答】解:由题意得:AE=AD=,
由勾股定理得:BE==1,
∴AB=BE,
∴∠BAE=45°,
∴∠DAE=45°,
∴的长==π,
故答案为:π.
8.【解答】解:∵四边形ABCD内接于⊙O,
∴∠A=∠DCE=70°,
∴∠BOD=2∠A=140°.
故答案为140°.
9.【解答】解:连接OP、OQ.
∵PQ是⊙O的切线,
∴OQ⊥PQ;
根据勾股定理知PQ2=OP2﹣OQ2,
∴当PO⊥AB时,线段PQ最短,
∵在Rt△AOB中,OA=OB=3,
∴AB=OA=6,
∴OP==3,
∴PQ===2.
故答案为:2.
10.【解答】解:连接OC,
∵AB是⊙O的直径,弦CD⊥AB,
∴CD=2CE,∠OEC=90°,
∵AB=10,AE=1,
∴OC=5,OE=5﹣1=4,
在Rt△COE中,CE==3,
∴CD=2CE=6,
故答案为:6.
11.【解答】解:由题意可知:2m2﹣3m﹣1=0,
∴2m2﹣3m=1,
∴原式=2(2m2﹣3m)+2019=2021.
故答案为:2021.
12.【解答】解:根据题中的新定义得:3☆x=9+x2,x★12=6x,
所求方程化为:9+x2=6x,即(x﹣3)2=0,
解得:x1=x2=3.
故答案为:x1=x2=3
13.【解答】解:设人行通道的宽度为x米,将两块矩形绿地合在一起长为(30﹣3x)m,宽为(24﹣2x)m,
由已知得:(30﹣3x)•(24﹣2x)=480,
整理得:x2﹣22x+40=0,
解得:x1=2,x2=20,
当x=20时,30﹣3x=﹣30,24﹣2x=﹣16,不符合题意舍去,
即x=2.
答:人行通道的宽度为2米.
故答案为:2.
14.【解答】解:如图,连接OD,
由翻折的性质可知,OB=BD,
∴OB=BD=OD,
∴∠BOD=∠OBD=∠ODB=60°,
∴∠AOD=∠AOB﹣∠BOD
=110°﹣60°
=50°,
即弧AD的度数为50°,
故答案为:50°.
三.解答题(共8小题)
15.【解答】解:(1)20+2×2=24(件).
故答案为:24.
(2)设当每件商品降价x元时,该商店每天销售利润为1050元,则每件盈利(40﹣x)元,平均每天的销售量为(20+2x)件,
依题意得:(40﹣x)(20+2x)=1050,
整理得:x2﹣30x+125=0,
解得:x1=5,x2=25.
当x=5时,40﹣x=35>25,符合题意;
当x=25时,40﹣x=15<25,不合题意,舍去.
答:当每件商品降价5元时,该商店每天销售利润为1050元.
16.【解答】(1)证明:连接OE,
∴OA=OE,
∴∠OEA=∠OAE.
∵PQ切⊙O于E,
∴OE⊥PQ.
∵AC⊥PQ,
∴OE∥AC.
∴∠OEA=∠EAC,
∴∠OAE=∠EAC,
∴AE平分∠BAC.
(2)解:过点O作OM⊥AC于M,
∴AM=MD==2;
又∠OEC=∠ACE=∠OMC=90°,
∴四边形OECM为矩形,
∴OM=EC=4,
在Rt△AOM中,OA===2;
即⊙O的半径为2.
17.【解答】解:(1)设y与销售单价x之间的函数关系式为:y=kx+b,
将点(30,100)、(45,70)代入一次函数表达式得:,
解得:,
故函数的表达式为:y=﹣2x+160;
(2)由题意得:(x﹣30)(﹣2x+160)=800,
解得:x1=40,x2=70,
∵销售单价不低于成本价,且不高于60元,
∴x=40,
∴y=﹣2x+160=﹣2×40+160=80(件).
答:每天的销售量应为80件.
18.【解答】解:(1)∵∠AOC=60°,AO=AC,
∴△AOC是等边三角形,
∴∠OAC=60°.
(2)∵CP与⊙A相切,
∴∠ACP=90°,
∴∠APC=90°﹣∠OAC=30°;
又∵A(4,0),
∴AC=AO=4,
∴PA=2AC=8,
∴PO=PA﹣OA=8﹣4=4.
(3)①过点C作CP1⊥OB,垂足为P1,延长CP1交⊙A于Q1;
∵OA是半径,
∴,
∴OC=OQ1,
∴△OCQ1是等腰三角形;
又∵△AOC是等边三角形,
∴P1O=OA=2;
②过A作AD⊥OC,垂足为D,延长DA交⊙A于Q2,CQ2与x轴交于P2;
∵A是圆心,
∴DQ2是OC的垂直平分线,
∴CQ2=OQ2,
∴△OCQ2是等腰三角形;
过点Q2作Q2E⊥x轴于E,
在Rt△AQ2E中,
∵∠Q2AE=∠OAD=∠OAC=30°,
∴Q2E=AQ2=2,AE=2,
∴点Q2的坐标(4+,﹣2);
在Rt△COP1中,
∵P1O=2,∠AOC=60°,
∴,
∴C点坐标(2,);
设直线CQ2的关系式为y=kx+b,则
,
解得,
∴y=﹣x+2+2;
当y=0时,x=2+2,
∴P2O=2+2.
19.【解答】解:(1)20+2×4=28(件).
故答案为:28.
(2)设每件商品降价x元,则每件盈利(40﹣x)元,平均每天可售出(20+2x)元,
依题意得:(40﹣x)(20+2x)=1200,
整理得:x2﹣30x+200=0,
解得:x1=10,x2=20,
又∵40﹣x≥25,
∴x≤15,
∴x=10.
答:当每件商品降价10元时,该商店每天销售利润为1200元.
20.【解答】解:设x2+3x=y,
则原方程可化为:y2+4y+3=0,
解得:y1=﹣1,y2=﹣3,
∴x2+3x=﹣1或x2+3x=﹣3,
当x2+3x+1=0时,
解得x1=,x2=;
当x2+3x+3=0时,
此方程无实数根,
21.【解答】解:(1)如图1,过点B作BC⊥x轴于点C,
∵点B在直线y=x的图象上,
∴BC=OC,
∴△OBC为等腰直角三角形,
∴∠BOC=45°,即直线OB与x轴所夹的锐角度数为45°,
故答案为:45;
(2)如图2,当⊙A′与直线OB相切于点M时,A′M⊥OB,
∵∠MOA′=45°,
∴OM=A′M=1,
∴OA′=,
∴A′A=3,
此时,t=3,
当⊙A′′与直线OB相切于点N时,A′′N⊥OB,
同理可得,A′′A=5,
此时,t=5,
综上所述,⊙A与直线OB相切时,t的值为3或5;
(3)如图3,设⊙A′与直线OB交于点C、D,过点A′作A′E⊥OB于点E,
则CE=DE=,
∴A′E==,
则OA′=A′E=,
∴A′A=4﹣,
同理可得,A′′A=4+,
综上所述,当⊙A与直线OB相交所得的弦长为1时,t的值为4﹣或4+,
故答案为:4﹣或4+.
22.【解答】解:(1)∵P从点A开始沿边AB向终点B以1cm/s的速度移动,
∴AP=tcm,
∵AB=5cm,
∴PB=(5﹣t)cm,
∵点Q从点B开始沿边BC向终点C以2cm/s的速度移动,
∴BQ=2tcm;
(2)由题意得:(5﹣t)2+(2t)2=52,
解得:t1=0,t2=2;
当t=0秒或2秒时,PQ的长度等于5cm;
(3)存在t=1秒,能够使得五边形APQCD的面积等于26cm2.理由如下:
长方形ABCD的面积是:5×6=30(cm2),
使得五边形APQCD的面积等于26cm2,则△PBQ的面积为30﹣26=4(cm2),
(5﹣t)×2t×=4,
解得:t1=4(不合题意舍去),t2=1.
即当t=1秒时,使得五边形APQCD的面积等于26cm2.
江苏淮安市凌桥中学2024-2025学年八上数学第7周阶段性训练模拟练习【含答案】: 这是一份江苏淮安市凌桥中学2024-2025学年八上数学第7周阶段性训练模拟练习【含答案】,共17页。试卷主要包含了下列各组数中,是勾股数的是等内容,欢迎下载使用。
江苏淮安市凌桥中学2024-2025学年八上创优班数学几何最值问题-专项训练【含答案】: 这是一份江苏淮安市凌桥中学2024-2025学年八上创优班数学几何最值问题-专项训练【含答案】,共23页。
江苏淮安市凌桥中学2024-2025学年七上数学第7周阶段性训练模拟练习【含答案】: 这是一份江苏淮安市凌桥中学2024-2025学年七上数学第7周阶段性训练模拟练习【含答案】,共14页。试卷主要包含了计算等内容,欢迎下载使用。












