



人教版(2024)八年级上册13.4课题学习 最短路径问题同步测试题
展开知识点01 最短路径的基本原理
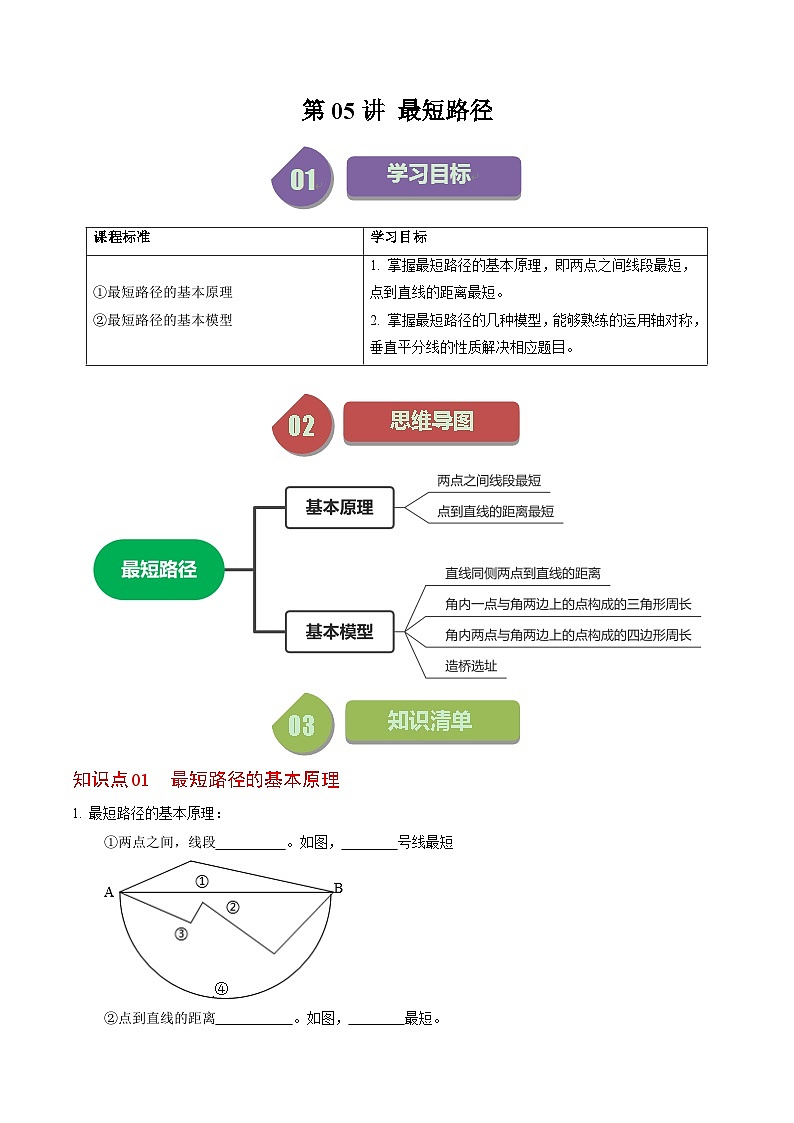
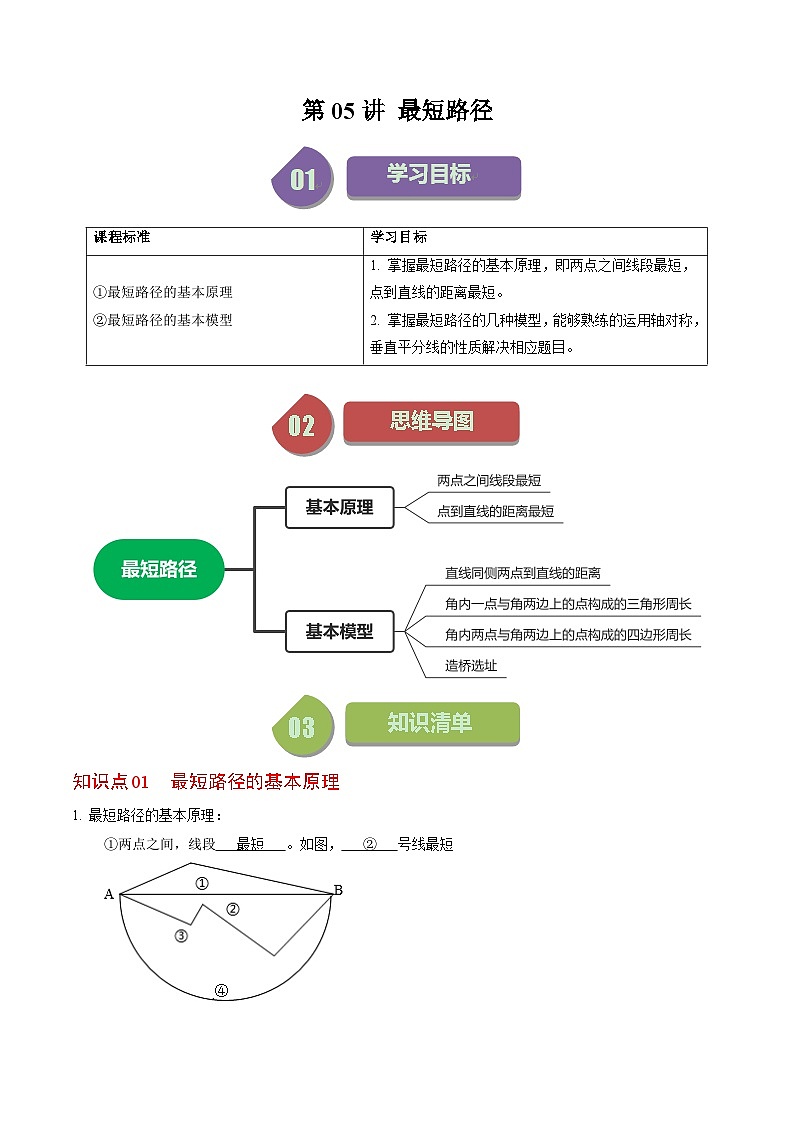
最短路径的基本原理:
①两点之间,线段 。如图, 号线最短
②点到直线的距离 。如图, 最短。
③垂直平分线上任意一点到线段两端点的距离 。如图,MN是垂直平分线,CA= 。
知识点02 最短路径的基本类型1——直线上一点到同侧两点的距离之和最短
如图,存在直线l以及直线外的点P和点Q,直线l上存在一点M,使得MP+MQ的值最小:
方法点拨:作其中一点关于直线的对称点,连接对称点与另一点,线段与直线的交点即为要找的点M。
解:如图,作点P关于直线l的对称点p’。连接P’ Q,P’ Q与直线l交于点M,则此时MP+MQ最小。
证明:∵P与P’关于直线l对称
∴直线l是PP’的
∴MP MP’
∴MP+MQ= +MQ= 。
∴MP+MQ此时有最小值,为 的长度
题型考点:①基本作图。②求值计算。
【即学即练1】
1.如图,在正方形网格中有M,N两点,在直线l上求一点P使PM+PN最短,则点P应选在( )
A.A点B.B点C.C点D.D点
【即学即练2】
2.如图,在等边△ABC中,BC边上的高AD=6,E是高AD上的一个动点,F是边AB的中点,在点E运动的过程中,EB+EF存在最小值,则这个最小值是( )
A.5B.6C.7D.8
知识点03 最短路径基本类型——角内一点与角两边构成的三角形周长最短
如图,已知∠MON以及角内一点P,角的两边OM与ON上存在点A与点B,使得△PAB的周长最小:
方法点拨:分别作点P关于OM与ON的对称点P’与P’’,连接P’ P’’。P’ P’’与OM、ON的交点A与B即为要找到的点。
解:如图,分别作点P关于OM与ON的对称点P’与P’’,连接P’ P’’。P’ P’’与OM、ON的分别交于点A与点B,连接PA、PB以及AB,此时△PAB的周长最小。
证明:∵P与P’关于OM对称,P与P’’关于ON对称
∴OM是PP’的 ,ON是PP’’的 。
∴AP AP’,BP BP’’
∴= +AB+ =
∴△PAB的周长最小。
题型考点:①基本作图。②求值计算。
【即学即练1】
3.如图,已知∠O,点P为其内一定点,分别在∠O的两边上找点A、B,使△PAB周长最小的是( )
A.B.
C.D.
【即学即练2】
4.如图,已知∠AOB的大小为α,P是∠AOB内部的一个定点,且OP=5,点E、F分别是OA、OB上的动点,若△PEF周长的最小值等于5,则α=( )
A.30°B.45°C.60°D.90°
知识点04 最短路径基本类型——角内两点与角两边构成的四边形周长最短
如图:已知∠AOB以及角内两点点P与点Q,角的两边上分别存在M、N使得四边形PQMN的周长最小:
方法点拨:分别作点关于较近直线的对称点,连接两个对称点的线段与边OA与OB相交与点M与点N,此时点M与点N即为要找的点。
解:如图,作点Q关于OA的对称点D,点P关于OB的对称点C,连接DC,DC与OA交于点M,与OB交于点N,连接QM,MN,PN,PQ。此时四边形PQMN的周长最下。
证明:∵Q与D关于OA对称,P与C关于OB对称
∴OA是QD的 ,OB是PC的 。
∴MD MQ,NP NC。
=PQ+ +MN+
=PQ+ 。
∴四边形PQMN的周长最小。
题型考点:①基本作图。
【即学即练1】
5.已知:∠AOB,点M和点N,试在OA、OB上分别找点P、Q,使四边形MNQP的周长最短.(尺规作图,不需写作法,保留作图痕迹)
知识点05 最短路径基本类型——造桥选址问题
如图:平行河岸两侧各有一村庄P、Q,现在河上修建一座垂直于河岸的桥,使得村庄P到村庄Q的路程最短:
方法点拨:在其中一个村庄作垂直于河岸的直线,使其长度等于桥的长度,连接端点与另一村庄,直线与另一村庄岸边的交点即为选址地点。如下图:
题型考点:①基本作图。
【即学即练1】
6.如图,A和B两地在一条河的两岸,现要在河上造一座桥MN,使从A到B的路径AMNB最短的是(假定河的两岸是平行直线,桥要与河岸垂直)( )
A.B.
C.D.
题型01 最短路径的作图
【典例1】
小王准备在红旗街道旁建一个送奶站,向居民区A,B提供牛奶,要使A,B两小区到送奶站的距离之和最小,则送奶站C的位置应该在( )
A.B.
C.D.
【典例2】
如图,河道l的同侧有M,N两个村庄,计划铺设管道将河水引至M,N两村,下面四个方案中,管道总长度最短的是( )
A.B.
C.D.
【典例3】
如图,直线l1,l2表示一条河的两岸,且l1∥l2.现要在这条河上建一座桥(桥与河的两岸相互垂直),使得从村庄P经桥过河到村庄Q的路程最短,应该选择路线( )
A.路线:PF→FQB.路线:PE→EQ
C.路线:PE→EF→FQD.路线:PE→EF→FQ
【典例4】
将军要检阅一队士兵,要求(如图所示);队伍长为a,沿河OB排开(从点P到点Q);将军从马棚M出发到达队头P,从P至Q检阅队伍后再赶到校场N.请问:在什么位置列队(即选择点P和Q),可以使得将军走的总路程MP+PQ+QN最短?
【典例5】
如图,山娃星期天从A处赶了几只羊到草地l1放羊,然后赶羊到小河l2饮水,之后再回到B处的家,假设山娃赶羊走的都是直路,请你为它设计一条最短的路线,标明放羊与饮水的位置.
【典例6】
如图:要求在l1、l2上找出M,N两点.使四边形PQNM的周长最小,在图上画出M,N的位置.(不写画法,保留作图痕迹)
题型02 最短路径的计算
【典例1】
如图,等边△ABC中,D为AC中点,点P、Q分别为AB、AD上的点,且BP=AQ=4,QD=3,在BD上有一动点E,则PE+QE的最小值为( )
A.7B.8C.10D.12
【典例2】
如图,CD是△ABC的角平分线,△ABC的面积为12,BC长为6,点E,F分别是CD,AC上的动点,则AE+EF的最小值是( )
A.6B.4C.3D.2
【典例3】
如图,四边形ABCD中,∠BAD=a,∠B=∠D=90°,在BC、CD上分别找一点M、N,当△AMN周长最小时,则∠MAN的度数为( )
A.aB.2a﹣180°C.180°﹣aD.a﹣90°
【典例4】
如图,∠AOB=30°,点D是它内部一点,OD=m.点E,F分别是OA,OB上的两个动点,则△DEF周长的最小值为( )
A.0.5mB.mC.1.5mD.2m
【典例5】
如图,直线m是△ABC中BC边的垂直平分线,点P是直线m上一动点,若AB=7,AC=6,BC=8,则△APC周长的最小值是( )
A.13B.14C.15D.13.5
【典例6】
如图,在△ABC中,AB=AC,BC=6,△ABC的面积是24,AB的垂直平分线ED分别交AC,AB边于E、D两点,若点F为BC边的中点,点P为线段ED上一动点,则△PBF周长的最小值为( )
A.7B.9C.11D.14
【典例7】
如图,边长为a的等边△ABC中,BF是AC上中线且BF=b,点D在BF上,连接AD,在AD的右侧作等边△ADE,连接EF,则△AEF周长的最小值是( )
A.B.C.a+bD.a
【典例8】
如图,在四边形ABCD中,∠C=α°,∠B=∠D=90°,E,F分别是BC,DC上的点,当△AEF的周长最小时,∠EAF的度数为( )
A.αB.2αC.180﹣αD.180﹣2α
课程标准
学习目标
①最短路径的基本原理
②最短路径的基本模型
掌握最短路径的基本原理,即两点之间线段最短,点到直线的距离最短。
掌握最短路径的几种模型,能够熟练的运用轴对称,垂直平分线的性质解决相应题目。
人教版八年级数学下册同步精讲精练专题用勾股定理解决最短路径问题(原卷版+解析): 这是一份人教版八年级数学下册同步精讲精练专题用勾股定理解决最短路径问题(原卷版+解析),共39页。试卷主要包含了用计算法求平面中的最短问题,用平移法求平面中的最短问题,用对称法求平面的最短问题,用展开图求长方体中的最短问题,用展开图求圆柱体的最短问题等内容,欢迎下载使用。
人教版八年级数学上册专题05最短路径的三种考法(原卷版+解析): 这是一份人教版八年级数学上册专题05最短路径的三种考法(原卷版+解析),共35页。试卷主要包含了坐标系的最值问题,几何图形中的最短路径问题,最短路径问题的实际应用等内容,欢迎下载使用。
人教版九年级数学下册同步精品讲义 第05讲 位似(原卷版+解析): 这是一份人教版九年级数学下册同步精品讲义 第05讲 位似(原卷版+解析),共43页。试卷主要包含了3 位似,位似图形,位似变换的坐标特点,画位似图形的一般步骤等内容,欢迎下载使用。













