2024-2025高一上期中考试复习数学讲义——函数

这是一份2024-2025高一上期中考试复习数学讲义——函数，文件包含第四讲函数常考知识复习讲义解析版docx、第四讲函数常考知识复习讲义解析版pdf、第四讲函数常考知识复习讲义学生版docx、第四讲函数常考知识复习讲义学生版pdf等4份试卷配套教学资源，其中试卷共153页， 欢迎下载使用。
模块二：典型例题
题型一：求具体函数与抽象函数的定义域
题型二：求函数的解析式
题型三：求函数的值域
题型四：函数的单调性
题型五：函数的奇偶性
题型六：函数性质的综合应用
题型七：幂函数
题型八：函数的实际应用
模块三：数学思想方法
①分类讨论思想②转化与化归思想③数形结合思想
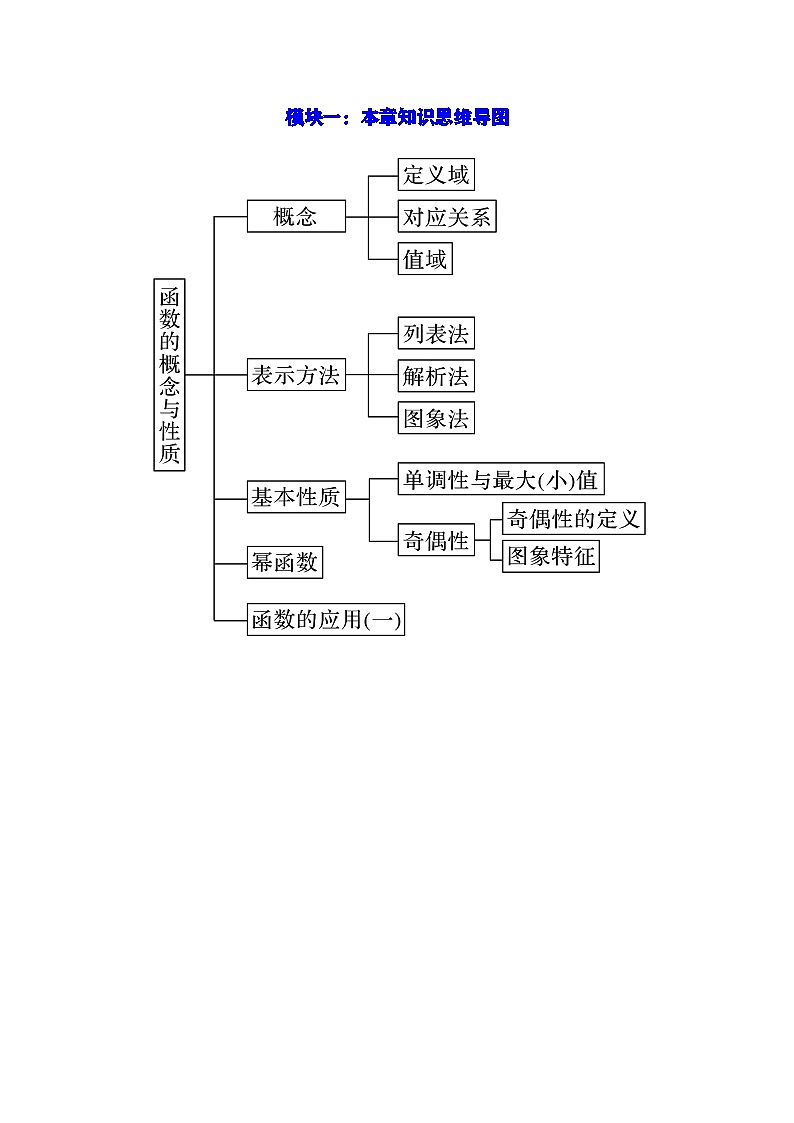
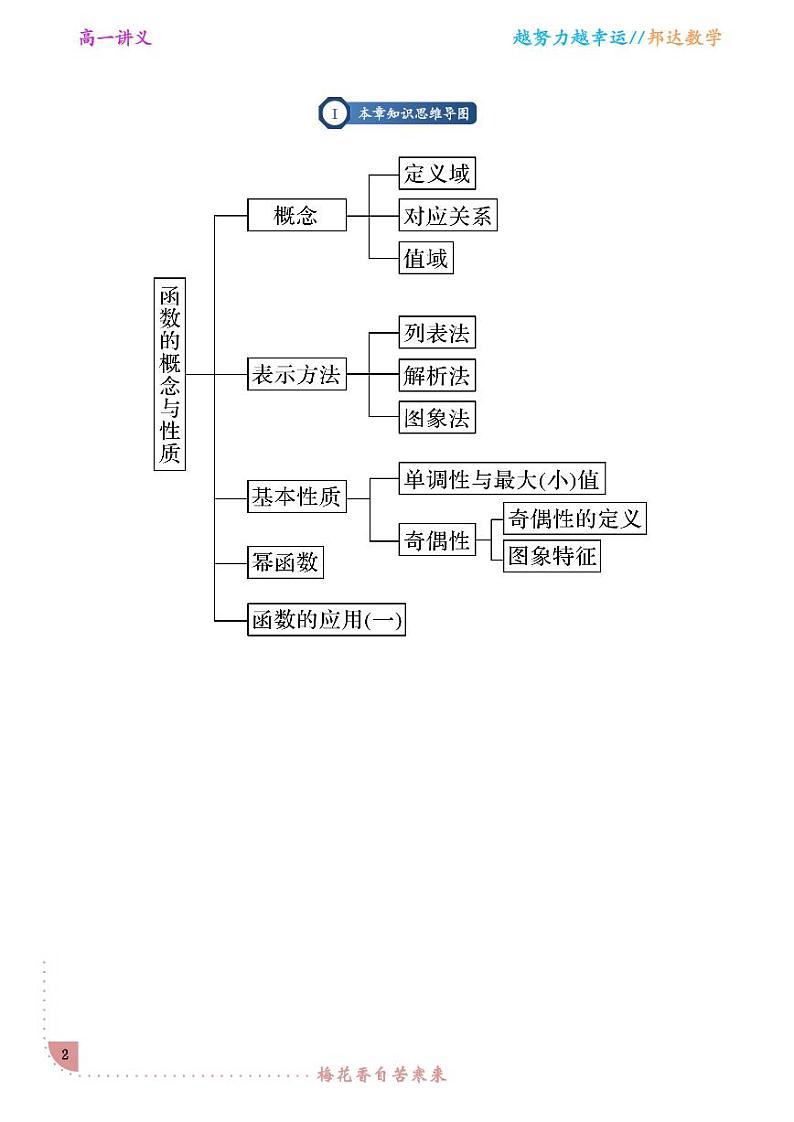
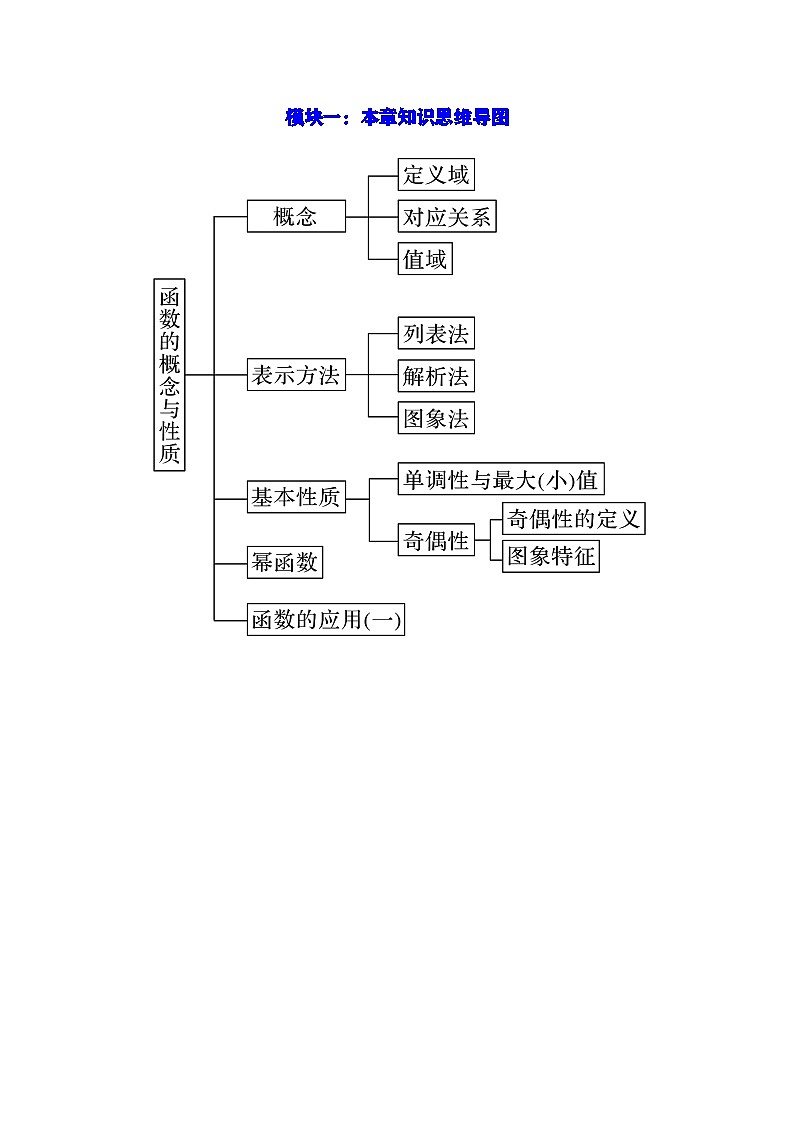
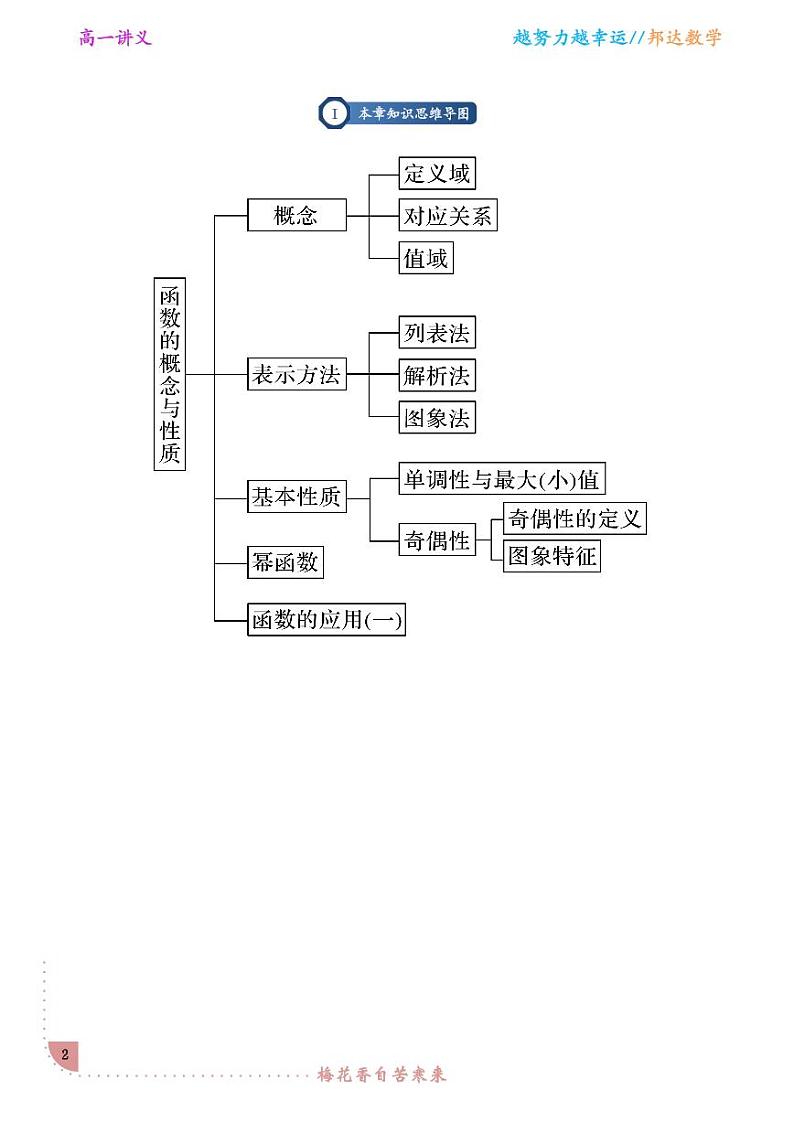
模块一：本章知识思维导图
模块二：典型例题
题型一：求具体函数与抽象函数的定义域
例1．（2024·广东深圳·高一校考期中）函数的定义域是 .
例2．（2024·上海松江·高一校考期末）函数的定义域为 （用区间表示）.
例3．（2024·河南新乡·高一校联考期末）函数的定义域为 ．
例4．（2024·新疆乌鲁木齐·高一校考期中）若函数的定义域为，则函数的定义域是 ．
例5．（2024·高一课时练习）已知函数的定义域是，则函数的定义域是 ．
例6．（2024·吉林长春·高一长春市解放大路学校校考阶段练习）已知函数的定义域为，则函数的定义域为 .
例7．（2024·全国·高一专题练习）已知函数的定义域为，则的定义域为 .
例8．（2024·全国·高一专题练习）已知函数的定义域为 则的定义域为
例9．（2024·全国·高一专题练习）已知函数的定义域为，则函数的定义域为 .
例10．（2024·全国·高一专题练习）函数的定义域为，则函数的定义域是 .
题型二：求函数的解析式
例11．（2024·河南郑州·高一校考阶段练习）已知函数是一次函数且，则函数的解析式为 ．
例12．（2024·全国·高一专题练习）已知是二次函数．且．则 ．
例13．（2024·四川眉山·高一校考阶段练习）已知，则 ．
例14．（2024·高一课时练习）已知函数，则函数的解析式是 .
例15．（2024·全国·高一专题练习）已知，则 .
例16．（2024·江苏盐城·高一统考期中）已知函数满足，则= .
例17．（2024·全国·高一专题练习）已知，则 ．
例18．（2024·上海·高一专题练习）已知函数满足，其中且，则函数的解析式为
例19．（2024·高一课时练习）已知函数满足，则的解析式为 .
题型三：求函数的值域
例20．（2024·全国·高一专题练习）求下列函数的值域.
(1);
(2);
(3)，
(4)
例21．（2024·高一课时练习）求下列函数的值域．
(1)；
(2)；
(3).
例22．（2024·高一课时练习）求下列函数的值域．
(1)；
(2)；
(3)；
(4).
例23．（2024·全国·高一课堂例题）求下列函数的值域：
(1)，；
(2)，；
(3)；
(4)；
(5)；
(6)；
(7)．
例24．（2024·高一校考课时练习）求下列函数的值域:
(1)，
(2)，
(3)，
(4)
题型四：函数的单调性
例25．（2024·高一课时练习）定义域为的函数在区间上是增函数，在区间上是减函数，则：
（1）函数的单调递增区间是 ；单调递减区间是 ；
（2）函数的单调递增区间是 ；单调递减区间是 ．
例26．（2024·山东·高一山东省实验中学校考阶段练习）函数的单调递增区间为 .
例27．（2024·全国·高一专题练习）已知函数，则的递减区间是 .
例28．（2024·黑龙江齐齐哈尔·高一校联考期中）函数在R上单调递减，则实数a的取值范围是 .
例29．（2024·全国·高一课堂例题）已知函数在上单调递减，对任意，均有，记，，则函数的最小值为 ．
例30．（2024·安徽安庆·高一安庆市第七中学校考期中）若在区间上是增函数，则实数a的取值范围是 .
例31．（2024·全国·高一专题练习）设函数，若存在最大值，则实数a的取值范围为 ．
例32．（2024·全国·高一专题练习）函数在区间上的最大值为，则 ．
例33．（2024·湖北武汉·高一校联考期中）函数是定义在上的增函数，若对于任意正实数，恒有，且，则不等式的解集是 .
例34．（2024·全国·高一专题练习）已知函数的定义域为，对任意的、，且都有成立，若对任意恒成立，则实数的取值范围是 ．
例35．（2024·全国·高一假期作业）定义在R上的函数f（x）的图象关于直线x＝2对称，且f（x）在（－∞，2）上是增函数，则f（－1）与f（3）的大小关系是 ．
例36．（2024·全国·高一课堂例题）证明函数在区间上递减，在区间上递增，并指出函数在区间上的最值点和最值．
例37．（2024·全国·高一专题练习）已知函数f（x）对任意的实数x、y都有f（x＋y）＝f（x）＋f（y）－1，且当x>0时，f（x）>1.求证：函数f（x）在R上是增函数.
例38．（2024·河北邯郸·高一校考期末）已知定义在上的函数满足：①对任意的，都有；②当且仅当时，成立．
(1)求；
(2)用定义证明的单调性；
例39．（2024·天津·高一统考期中）已知函数是奇函数，且.
(1)求的解析式；
(2)判断在区间上的单调性并说明理由.
题型五：函数的奇偶性
例40．（2024·新疆巴音郭楞·高一八一中学校考期中）已知（，且），．
(1)求的值；
(2)判断函数的奇偶性；
(3)证明函数在上是增函数．
例41．（2024·湖南株洲·高一株洲二中校考阶段练习）已知定义在上的奇函数，且.
(1)求函数的解析式;
(2)判断的单调性（并用单调性定义证明）;
(3)解不等式.
例42．（2024·全国·高一随堂练习）判断下列函数是否具有奇偶性：
(1)；
(2)；
(3)；
(4)；
(5)；
(6).
例43．（2024·全国·高一期中）已知函数，且.
(1)求实数的值；
(2)判断该函数的奇偶性；
(3)判断函数在上的单调性，并证明.
例44．（2024·甘肃白银·高一校考期中）已知函数，.
(1)若在上为偶函数，求，的值；
(2)设的定义域为，在（1）的条件下：
①判断函数在定义域上的单调性并证明；
②若，求实数t的取值范围.
例45．（2024·全国·高一期中）已知定义在,,上的函数满足：①，,,，；②当时，，且．
(1)试判断函数的奇偶性；
(2)判断函数在上的单调性；
(3)求函数在区间,,上的最大值；
(4)求不等式的解集．
例46．（2024·江西南昌·高一南昌市八一中学校考阶段练习）已知函数是定义在上的奇函数，当时，，其中
(1)求函数的解析式；
(2)若函数在区间不单调，求出实数的取值范围.
例47．（2024·黑龙江牡丹江·高一牡丹江市第二高级中学校考期末）设函数是增函数，对于任意x，都有．
(1)写一个满足条件的并证明；
(2)证明是奇函数；
(3)解不等式．
题型六：函数性质的综合应用
例48．（多选题）（2024·黑龙江齐齐哈尔·高一校联考期中）函数，，用表示，中的较大者，记为，则下列说法正确的是（ ）
A．B．，
C．有最大值D．最小值为0
例49．（多选题）（2024·江苏南通·高一统考期末）奇函数与偶函数的定义域均为，在区间上都是增函数，则（ ）
A．
B．在区间上是增函数，在区间上是减函数
C．是奇函数，且在区间上是增函数
D．不具有奇偶性，且在区间上的单调性不确定
例50．（多选题）（2024·福建福州·高一校联考期中）已知连续函数对任意实数恒有，当时，，，则（ ）
A．B．在上的最大值是4
C．图像关于中心对称D．不等式的解集为
例51．（多选题）（2024·江西赣州·高一统考期中）世界公认的三大著名数学家为阿基米德、牛顿、高斯，其中享有“数学王子”美誉的高斯提出了取整函数，表示不超过的最大整数，例如，．已知函数，则（ ）
A．在上是增函数B．
C．为奇函数D．的值域为
例52．（多选题）（2024·全国·高一专题练习）已知定义域为的函数满足：，，且，则下列结论成立的是（ ）
A．B．为偶函数C．为奇函数D．
例53．（多选题）（2024·全国·高一专题练习）设函数是定义在上的函数，并且满足下面三个条件：①对正数，都有；②当时，；③.则下列说法不正确的是（ ）
A．
B．
C．不等式的解集为
D．若关于x的不等式恒成立，则的取值范围是
例54．（多选题）（2024·重庆长寿·高一统考期末）若函数在定义域内内的某区间是增函数，且在上是减函数，则称在上是“弱增函数”，则下列说法正确的是（ ）
A．若则不存在区间使为“弱增函数”
B．若则存在区间使为“弱增函数”
C．若则为上的“弱增函数”
D．若在区间上是“弱增函数”，则
例55．（2024·福建漳州·高一校考期中）已知定义在区间上的函数．
(1)若函数分别在区间上单调，试求的取值范围；（直接写出答案）
(2)当时，在区间上是否存在实数，使得函数在区间上单调，且的取值范围为，若存在，求出的取值范围；若不存在，说明理由．
例56．（2024·全国·高一期中）已知函数
(1)设在区间的最小值为，求的表达式；
(2)设，若函数在区间上是增函数，求实数a的取值范围．
例57．（2024·高一单元测试）已知偶函数的定义域是的一切实数，对定义域内的任意都有，且当时，，.
(1)证明：在上是单调递增函数；
(2)解不等式.
题型七：幂函数
例58．（2024·全国·高一专题练习）已知幂函数满足：
①在上为增函数，
②对，都有，
求同时满足①②的幂函数的解析式，并求出时，的值域.
例59．（2024·浙江金华·高一校考期中）已知点在幂函数的图像上.
(1)求的解析式；
(2)若函数，是否存在实数a，使得最小值为5？若存在，求出a的值；若不存在，说明理由
例60．（2024·全国·高一假期作业）已知幂函数的图象关于y轴对称，且在上单调递增.
(1)求m和n的值；
(2)求满足不等式的a的取值范围.
例61．（2024·江苏南通·高一海安高级中学校考期中）已知幂函数为奇函数.
(1)求实数m的值；
(2)求函数（）的最小值.
例62．（2024·黑龙江七台河·高一勃利县高级中学校考期中）已知幂函数关于y轴对称，且在上单调减函数．
(1)求m的值；
(2)解关于a的不等式．
例63．（2024·广西柳州·高一柳铁一中校联考阶段练习）已知幂函数，且.
(1)求函数的解析式；
(2)试判断是否存在正数，使得函数在区间上的最大值为5，若存在，求出的值，若不存在，请说明理由.
例64．（2024·广东佛山·高一佛山市顺德区乐从中学校考期中）已知幂函数在上单调递增.
(1)求的解析式；
(2)若在上恒成立，求实数的取值范围．
例65．（2024·浙江杭州·高一校联考期中）已知幂函数为偶函数，且在区间上单调递增
(1)求函数的解析式;
(2)设函数，求函数在区间上的最小值
例66．（2024·福建漳州·高一福建省华安县第一中学校考阶段练习）已知幂函数是定义在R上的偶函数.
(1)求的解析式；
(2)在区间上，的图象总在函数图象的上方，求实数k的取值范围.
例67．（2024·重庆沙坪坝·高一重庆八中校考期中）已知幂函数，且.
(1)求函数的解析式；
(2)若均为正数且，求的最小值.
题型八：函数的实际应用
例68．（2024·全国·高一专题练习）党的十九大报告明确要求继续深化国有企业改革，培育具有全球竞争力的世界一流企业.某企业抓住机遇推进生产改革，从单一产品转为生产A、B两种产品，根据市场调查与市场预测，A产品的利润与投资成正比，其关系如图①；B产品的利润与投资的算术平方根成正比，其关系如图②（注：所示图中的横坐标表示投资金额，单位为万元）.

(1)分别求出A、B两种产品的利润表示为投资的函数关系式；
(2)该企业已筹集到10万元资金，并全部投入A、B两种产品的生产，问：怎样分配这10万元资金，才能使企业获得最大利润，最大利润是多少？
例69．（2024·全国·高一专题练习）某企业为进一步增加市场竞争力，计划在2024年利用新技术生产某款新手机，通过市场调研发现，生产该产品全年需要投入研发成本250万元，每生产（千部）手机，需另外投入成本万元，其中，已知每部手机的售价为5000元，且生产的手机当年全部销售完.
(1)求2024年该款手机的利润关于年产量的函数关系式；
(2)当年产量为多少时，企业所获得的利润最大？最大利润是多少？
例70．（2024·全国·高一专题练习）党的二十大报告提出“积极稳妥推进碳达峰碳中和”，降低能源消耗，建设资源节约型社会．日常生活中我们使用的灯具就具有节能环保的作用，它环保不含汞，可回收再利用，功率小，高光效，长寿命，有效降低资源消耗．经过市场调查，可知生产某种灯需投入的年固定成本为3万元，每生产万件该产品，需另投入变动成本万元，在年产量不足6万件时，，在年产量不小于6万件时，．每件产品售价为6元．假设该产品每年的销量等于当年的产量．
(1)写出年利润（万元）关于年产量（万件）的函数解析式．（注：年利润年销售收入固定成本变动成本）
(2)年产量为多少万件时，年利润最大？最大年利润是多少？
例71．（2024·全国·高一专题练习）某学校为了支持生物课程基地研究植物的生长规律，计划利用学校空地建造一间室内面积为的矩形温室，在温室内划出三块全等的矩形区域，分别种植三种植物，相邻矩形区域之间间隔1m，三块矩形区域的前、后与内墙各保留1m宽的通道，左、右两块矩形区域分别与相邻的左右内墙保留3m宽的通道，如图．设矩形温室的室内长为x（单位：m），三块种植植物的矩形区域的总面积为S（单位：）．
(1)求S关于x的函数关系式；
(2)求S的最大值，并求出此时x的值．
例72．（2024·江苏镇江·高一扬中市第二高级中学校考开学考试）党中央、国务院对节能减排高度重视，各地区、各部门认真贯彻党中央、国务院关于“十三五”节能减排的决策部署，把节能减排作为转换发展方式，经济提质增效，建设生态文明的重要抓手，取得重要进展.新能源汽车环保、节能、以电代油，减少排放，既符合我国国情，也代表了汽车产业发展的方向.为了响应国家节能减排的号召，2020年常州某企业计划引进新能源汽车生产设备，通过市场分析：全年需投入固定成本2500万元.每生产（百辆）新能源汽车，需另投入成本万元，且.由市场调研知，每辆车售价9万元，且生产的车辆当年能全部销售完.
（1）请写出2020年的利润（万元）关于年产量（百辆）的函数关系式；（利润＝销售－成本）
（2）当2020年产量为多少百辆时，企业所获利润最大？并求出最大利润.
例73．（2024·浙江衢州·高一校考阶段练习）年初，新冠肺炎疫情袭击全国，对人民生命安全和生产生活造成严重影响.为降低疫情影响，某厂家拟尽快加大力度促进生产.已知该厂家生产某种产品的年固定成本为万元，每生产千件，需另投入成本为，当年产量不足千件时，(万元).当年产量不小于千件时，(万元).每件商品售价为万元.通过市场分析，该厂生产的商品能全部售完.
（1）写出年利润(万元)关于年产量(千件)的函数解析式；
（2）当年产量为多少千件时，该厂在这一商品的生产中所获利润最大？最大利润是多少？
例74．（2024·高一课时练习）新冠肺炎疫情造成医用防护服短缺，某地政府决定为防护服生产企业A公司扩大生产提供(万元)的专项补贴，并以每套80元的价格收购其生产的全部防护服.A公司在收到政府x(万元)补贴后，防护服产量将增加到(万件)，其中k为工厂工人的复工率().A公司生产t万件防护服还需投入成本(万元).
（1）将A公司生产防护服的利润y(万元)表示为补贴x(万元)的函数(政府补贴x万元计入公司收入)；
（2）对任意的(万元)，当复工率k达到多少时，A公司才能不产生亏损？(精确到0.01).
例75．（2024·山西晋城·高一晋城市第一中学校校考阶段练习）新冠肺炎疫情造成医用防护服短缺，某地政府决定为防护服生产企业A公司扩大生产提供（万元）的专项补贴，并以每套80元的价格收购其生产的全部防护服．A公司在收到政府（万元）补贴后，防护服产量将增加到（万件），其中为工厂工人的复工率（）．A公司生产万件防护服还需投入成本（万元）．
（1）将A公司生产防护服的利润（万元）表示为补贴（万元）的函数（政府补贴x万元计入公司收入）；
（2）在复工率为k时，政府补贴多少万元才能使A公司的防护服利润达到最大？
模块三：数学思想方法
①分类讨论思想
例76．设函数，用表示，中的较大者，记为，则的最小值是（ ）
A．1B．3C．0D．
例77．已知幂函数满足，则函数的值域为（ ）
A．B．C．D．
例78．若定义在R的奇函数在单调递增，且，则满足的x的取值范围是（ ）
A．B．
C．D．
例79．已知函数的最小值为，则a的取值范围是（ ）
A．B．
C．D．
例80．已知函数，当时，的最大值为，则的取值范围是（ ）
A．B．C．D．
②转化与化归思想
例81．定义在R上的奇函数在上单调递减，且，则满足的x的取值范围是（ ）
A．B．C．D．
例82．已知函数，若，且，设，则t的最大值为（ ）
A． 1B．C．D．
例83．若定义在R的奇函数在单调递减，且，则满足的x的取值范围是（ ）
A．B．C．D．
例84．设，，，则（ ）
A．B．C．D．
例85．已知函数在区间上既没有最大值也没有最小值，则实数k的取值范围是
A．B．
C．D．
例86．函数的单调递增区间是（ ）
A．B．C．D．
③数形结合思想
例87．已知函数为奇函数，时为增函数且，则（ ）
A．或B．或
C．或D．或
例88．已知定义在R上的偶函数满足：①对任意的，且，都有成立；②则不等式的解集为（ ）
A．B．
C．D．
例89．已知函数的值域是，则实数m的取值范围是（ ）
A．B．C．D．
例90．奇函数在上单调递减，且，则不等式的解集是．（ ）
A．B．
C．D．
例91．如图，直线l和圆C，当l从开始在平面上绕点O按逆时针方向匀速转到转到角不超过时，它扫过的圆内阴影部分的面积S是时间t的函数，这个函数的图像大致是（ ）
A．B．
C．D．
例92．已知函数是定义在上的奇函数，且当时，函数的图像如图所示，则不等式的解集为（ ）
A．
B．
C．
D．