2024-2025高一上期中考试复习数学讲义——集合

这是一份2024-2025高一上期中考试复习数学讲义——集合，文件包含第一讲集合复习题解析版docx、第一讲集合复习题解析版pdf、第一讲集合复习题学生版docx、第一讲集合复习题学生版pdf等4份试卷配套教学资源，其中试卷共84页， 欢迎下载使用。
模块二：典型例题
题型一：集合的基本概念及表示
题型二：集合的基本关系
题型三：集合的交、并、补运算
题型四：利用子集关系求参数
题型五：子集、真子集的个数问题
题型六：韦恩图的应用
题型七：根据集合的交、并、补求参问题
题型八：补集思想及其应用
题型九：集合中的创新问题
模块三：数学思想方法
①分类讨论思想②转化与化归思想③数形结合思想
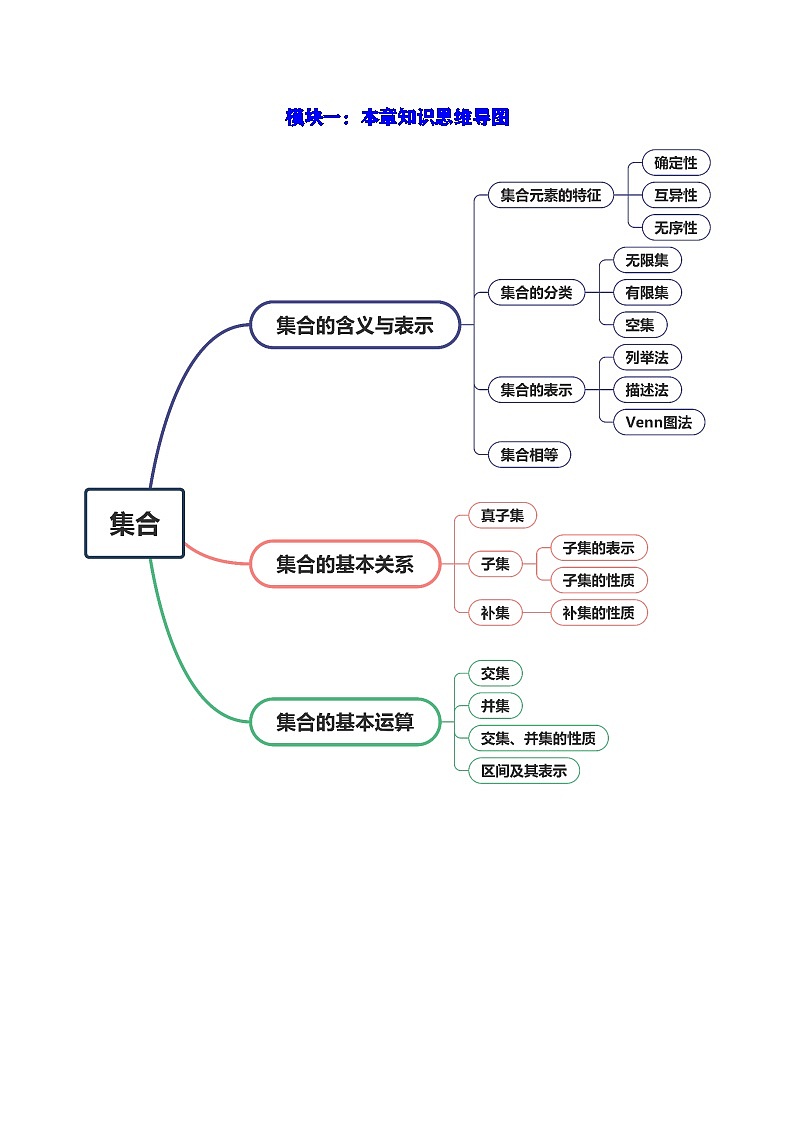
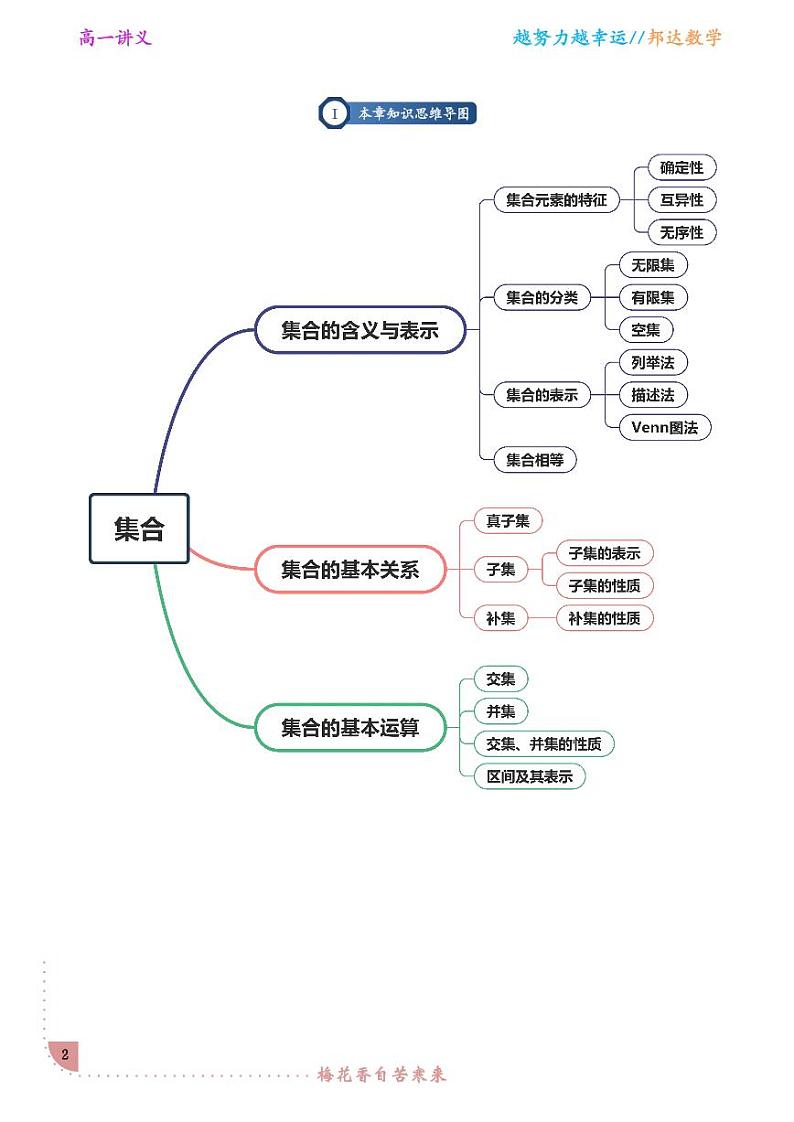
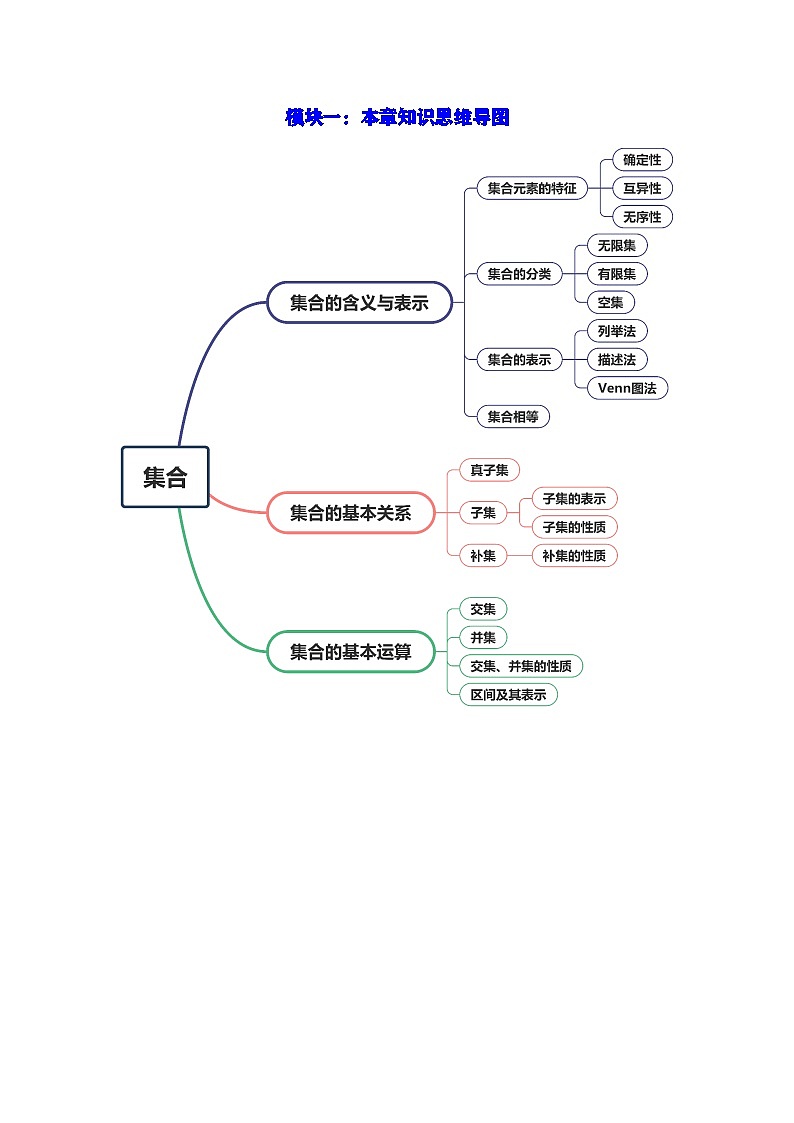
模块一：本章知识思维导图
模块二：典型题型
题型一：集合的基本概念及表示
例1．（2024·高一·全国·专题练习）下列四组集合中表示同一集合的为（ ）
A．，B．，
C．，D．，
例2．（2024·高一·新疆·阶段练习）下列对象中不能构成一个集合的是（ ）
A．某校比较出名的教师B．方程的根
C．不小于3的自然数D．所有锐角三角形
例3．（2024·高一·天津南开·期中）下列给出的对象能构成集合的有（ ）
①某校2023年入学的全体高一年级新生；②的所有近似值；
③某个班级中学习成绩较好的所有学生；④不等式的所有正整数解
A．1个B．2个C．3个D．4个
例4．（2024·高一·江苏淮安·开学考试）下列对象能构成集合的是（ ）
A．我国近代著名的数学家B．的所有近似值
C．所有的欧盟成员国D．2023年全国高考数学试题中所有难题
例5．（2024·高一·新疆乌鲁木齐·期中）给出四个结论：
①是由4个元素组成的集合；
②集合表示仅由一个“1”组成的集合；
③与是两个不同的集合；
④集合大于3的无理数是一个有限集．
其中正确的是（ ）
A．①④B．②④C．②③D．②
例6．（2024·高一·江苏淮安·阶段练习）下列命题中正确的是（ ）
①与表示同一个集合 ②方程的所有解的集合可表示为
③由1，2，3组成的集合可表示为或 ④集合可以用列举法表示
A．只有①和④B．只有②和③C．只有②D．只有③
例7．（2024·高一·上海·假期作业）用适当的方法表示下列集合：
(1)大于0且不超过10的全体偶数组成的集合；
(2)被3除余2的自然数全体组成的集合；
(3)直角坐标平面上由第二象限与第四象限中的所有点组成的集合.
题型二：集合的基本关系
例8．（2024·宁夏石嘴山·三模）已知集合，则与集合的关系为（ ）
A．B．C．D．
例9．（2024·全国·模拟预测）已知集合，则下列表示正确的是（ ）.
A．B．
C．D．
例10．（2024·高三·全国·专题练习）已知集合，且，则实数为（ ）
A．2B．3C．0或3D．
例11．（2024·高一·河南郑州·阶段练习）若，，，则这三个集合间的关系是（ ）
A．B．
C．D．
例12．（2024·高一·上海青浦·期末）已知非空集合且，设，，则对于的关系，下列问题正确的是（ ）
A．B．C．D．的关系无法确定
例13．（2024·高一·湖南长沙·阶段练习）设集合，，则下列关系正确的是（ ）
A．B．
C．D．P与Q无包含关系
题型三：集合的交、并、补运算
例14．（2024·高二·新疆·学业考试）设全集，集合，，则 .
例15．（2024·高一·西藏林芝·期中）已知全集，集合，.则= .
例16．（2024·高一·新疆·阶段练习）（1）已知集合，，．求，．
（2）已知集合或，．求，；
例17．（2024·高一·宁夏吴忠·期中）已知集合或，全集.
(1)求；
(2)求.
例18．（2024·高一·上海浦东新·阶段练习）设全集，若，，，则 ．
题型四：利用子集关系求参数
例19．（2024·高一·上海·期末）已知集合.
(1)若只有一个元素，试求实数的值，并用列举法表示集合；
(2)若至少有两个子集，试求实数的取值范围.
例20．（2024·高一·上海嘉定·期中）已知集合
(1)若A中只有一个元素，求a的值
(2)若A中至多有一个元素，求a的取值范围
(3)若，求a的取值范围
例21．（2024·高一·上海普陀·期中）已知集合，且满足，求实数可能取的一切值．
例22．（2024·高一·安徽安庆·阶段练习）已知集合
(1)若求实数的取值范围.
(2)是否存在实数，使得?若存在求出的值；若不存在，请说明理由.
例23．（2024·高一·山东·阶段练习）已知全集，集合或，．
(1)若，求的值；
(2)若，求的取值范围．
题型五：子集、真子集的个数问题
例24．（2024·高一·河南南阳·阶段练习）若{a，b}⊆A⫋{a，b，c，d}，则符合条件的集合A的个数为（ ）
A．3B．4C．7D．8
例25．（2024·高一·河南郑州·阶段练习）已知集合,，则满足条件的集合的个数为（ ）
A．2B．3C．4D．5
例26．（2024·高一·全国·专题练习）设，写出集合的子集，并指出其中哪些是它的真子集．
例27．（2024·高一·甘肃白银·阶段练习）设集合，求集合A的所有子集以及子集的的个数.
例28．（2024·高一·福建泉州·阶段练习）已知集合.
(1)写出集合M的子集、真子集;
(2)求集合N的子集数、真子集数和非空真子集数;
(3)猜想:含n个元素的集合的所有子集的个数是多少?真子集的个数及非空真子集的个数呢?
题型六：韦恩图的应用
例29．（2024·高二·湖南长沙·期末）已知某校高三（1）班有51名学生，春季运动会上，有17名学生参加了田赛项目，有22名学生参加了径赛项目，田赛和径赛都参加的有9名同学，则该班学生中田赛和径赛都没有参加的人数为（ ）
A．25B．23C．21D．19
例30．（多选题）（2024·河北石家庄·三模）某校“五一田径运动会”上，共有12名同学参加100米、400米、1500米三个项目，其中有8人参加“100米比赛”，有7人参加“400米比赛”，有5人参加“1500米比赛”，“100米和400米”都参加的有4人，“100米和1500米”都参加的有3人，“400米和1500米”都参加的有3人，则下列说法正确的是（ ）
A．三项比赛都参加的有2人B．只参加100米比赛的有3人
C．只参加400米比赛的有3人D．只参加1500米比赛的有1人
例31．（多选题）（2024·高一·江西·期末）如图，已知矩形表示全集，是的两个子集，则阴影部分可表示为（ ）

A．B．C．D．
例32．（多选题）（2024·高一·江西吉安·期末）如图，全集为U，集合A，B是U的两个子集，则阴影部分可表示为（ ）
A．B．
C．D．
例33．（多选题）（2024·高一·内蒙古赤峰·期中）图中阴影部分用集合表示正确的是（ ）

A．B．
C．D．
例34．（多选题）（2024·高一·河北石家庄·阶段练习）已如全集，集合，那么下列等式正确的是（ ）
A．B．C．D．
题型七：根据集合的交、并、补求参问题
例35．（2024·高一·辽宁·期中）已知全集 ，且．
(1)求集合M，N；
(2)若集合，求实数m的值．
例36．（2024·高一·福建厦门·期中）已知全集，集合，.
(1)当时，求；
(2)在①；②；③中任选一个条件，求实数的取值范围.
题型八：补集思想及其应用
例37．（2024·高一·甘肃临夏·期末）设，函数，的解集A．
(1)求集合A．
(2)若，，求实数a的取值范围．
例38．（2024·高一·安徽马鞍山·阶段练习）已知集合.
(1)求；
(2)若，求的取值范围.
例39．（2024·高一·浙江杭州·期中）设集合，，.
(1)若，求实数的值；
(2)若且，求实数的值.
例40．（2024·高一·辽宁·阶段练习）已知全集，，，.
(1)若，且，求的值及集合；
(2)若，求的值及.
例41．（2024·高一·江苏南京·阶段练习）设集合或，若，则实数a的取值范围是 ．
题型九：集合中的创新问题
例42．（2024·高二·全国·期末）设集合，集合，定义，则中元素个数是（ ）
A．7B．10C．D．
例43．（2024·广东深圳·模拟预测）定义两集合的差集：且，已知集合，，则的子集个数是（ ）个．
A．2B．4C．8D．16
例44．（2024·高一·四川成都·期末）已知A，B是两个非空集合，定义运算，且，，且.
(1)若，，求和；
(2)若，，求和.
例45．（2024·高一·山东泰安·阶段练习）已知集合．
(1)求；
(2)定义且，求．
例46．（2024·湖南怀化·二模）给定整数，有个实数元素的集合，定义其相伴数集，如果，则称集合为一个元规范数集．（注：表示数集中的最小数）．对于集合，则（ ）
A．是规范数集，不是规范数集B．是规范数集，是规范数集
C．不是规范数集，是规范数集D．不是规范数集，不是规范数集
例47．（2024·黑龙江·二模）已知集合，，定义集合：，则集合的非空子集的个数是（ ）个．
A．16B．15C．14D．13
例48．（2024·高三·湖北·阶段练习）已知集合，，若定义集合运算：，则集合的所有元素之和为（ ）
A．6B．3C．2D．0
模块三：数学思想方法
①分类讨论思想
例49．（2024·高一·全国·专题练习）设，，B不为空集，，求的值.
例50．（2024·江苏·高一假期作业）已知.若，则实数m的取值范围为 .
例51．（2024·高一·河北沧州·期中）已知集合.
(1)若集合，且，求的值；
(2)若集合，且与有包含关系，求的取值范围.
例52．（2024·高一课前预习）已知集合，，若，则 .
②转化与化归思想
例53．（2024·高一·四川遂宁·期中）设全集，已知集合，集合.
(1)求；
(2)若且，求实数a的取值范围.
例54．（2024·高一·全国·专题练习）若集合A共有5个元素，则A的真子集的个数为（ ）
A．32B．31C．16D．15
例55．（2024·高一·福建福州·阶段练习）已知集合，.
(1)若时，求；
(2)若，求实数的取值范围.
例56．（2024·江苏徐州·高一校考阶段练习）已知集合，，其中．
(1)若，求，的值；
(2)若对，有，求，的取值范围．
③数形结合思想
例57．（2024·上海徐汇·高一海市第二中学校考阶段练习）已知全集中有个元素，中有个元素．若非空，则的元素个数为 个．
例58．（2024·上海浦东新·高一校考阶段练习）已知是全集，是的三个子集，用交、并、补关系将图中的阴影部分表示出来 ．
例59．（2024·甘肃白银·高一校考阶段练习）已知全集U和集合A，B如图所示，则 ．
例60．（2024·高二·陕西咸阳·阶段练习）“扫码支付”“高铁”“网购”与“共享单车”被称为中国的“新四大发明”.某中学为了了解本校学生中“新四大发明”的普及情况，随机调查了100位学生，其中使用过“扫码支付”或“共享单车”的学生共有90位，使用过“扫码支付”的学生共有80位，使用过“共享单车”且使用过“扫码支付”的学生共有60位，则这100位学生中使用过“共享单车”的学生共有 位.
例61．（2024·高一·河南驻马店·阶段练习）为了坚持“五育”并举，全面发展素质教育，某学校在课余时间提供了多种社团供学生们选择，每位同学都可以选择多种社团，其中选择舞蹈社团或园艺社团的同学有90人，选择舞蹈社团的同学有55人，选择园艺社团的同学有60人，则同时选择舞蹈社团和园艺社团的同学人数是 .