



高中1.5.1 全称量词与存在量词精品同步达标检测题
展开一.全称量词与全称量词命题
二.存在量词与存在量词命题
三.含量词的命题的否定
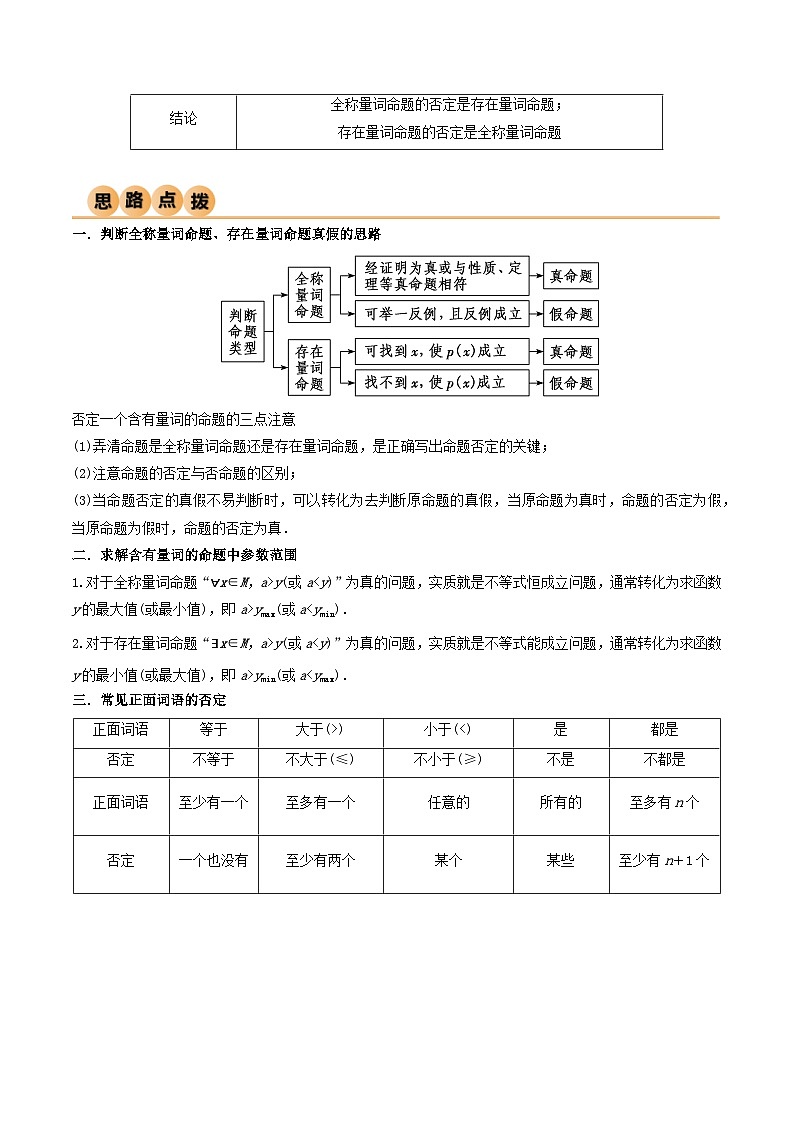
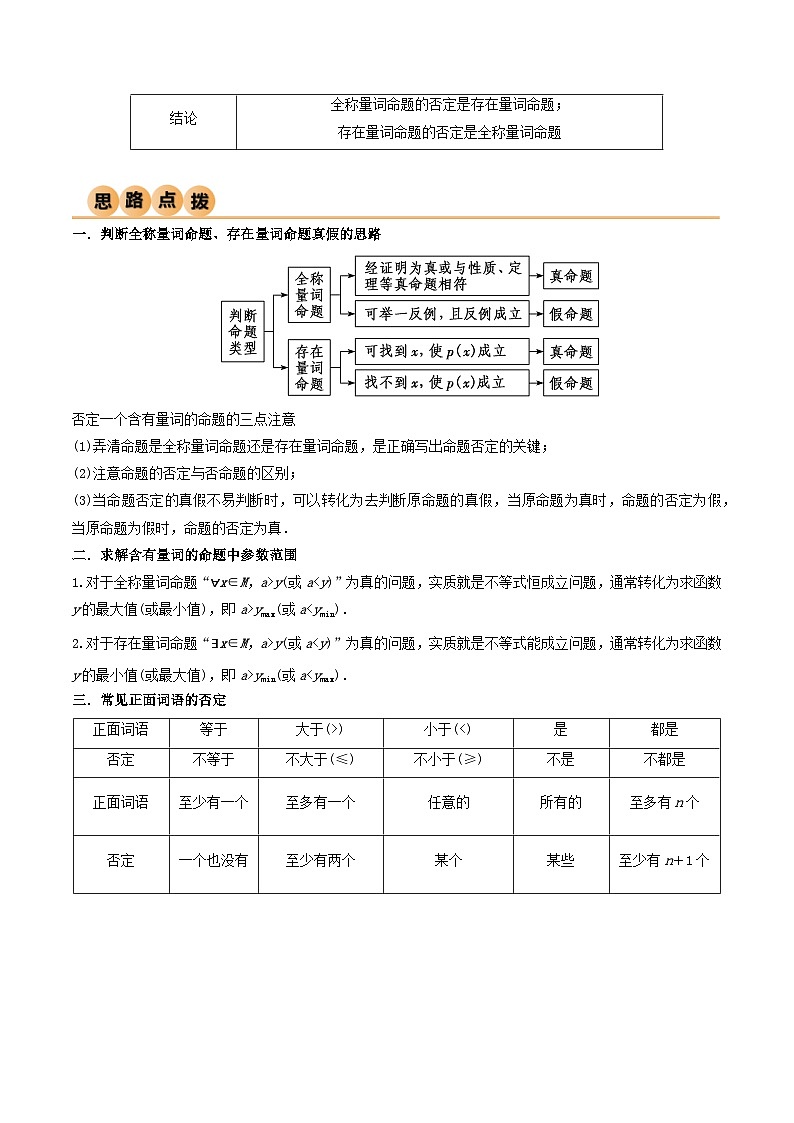
一.判断全称量词命题、存在量词命题真假的思路
否定一个含有量词的命题的三点注意
(1)弄清命题是全称量词命题还是存在量词命题,是正确写出命题否定的关键;
(2)注意命题的否定与否命题的区别;
(3)当命题否定的真假不易判断时,可以转化为去判断原命题的真假,当原命题为真时,命题的否定为假,当原命题为假时,命题的否定为真.
二.求解含有量词的命题中参数范围
1.对于全称量词命题“∀x∈M,a>y(或a
考点一 全称量词与存在量词
【例1-1】(2023·河南平顶山)下列语句不是存在量词命题的是( )
A.至少有一个x,使成立B.有的无理数的平方不是有理数
C.存在,是偶数D.梯形有两边平行
【例1-2】(2023·四川乐山)下列命题中,不是全称量词命题的是( )
A.任何一个实数乘以0都等于0B.自然数都是正整数
C.实数都可以写成小数形式D.存在奇数不是素数
【一隅三反】
1.(2023·广西)下列命题中,含有存在量词的是( )
A.存在一个平行四边形是矩形B.所有正方形都是平行四边形
C.一切三角形的内角和都等于D.任意两个等边三角形都相似
2.(2023·江苏南京)已知命题:①任何实数的平方都是非负数;②有些三角形的三个内角都是锐角;③每一个实数都有相反数;④所有数与0相乘,都等于0.其中,其中含存在量词的命题的个数是( )
A.1B.2C.3D.4
3.(2023·北京)下列命题中是存在量词命题的是( )
A.平行四边形的对边相等B.同位角相等
C.任何实数都存在相反数D.存在实数没有倒数
考点二 全称量词命题与存在量词命题的真假
【例2-1】(2022湖南)下列命题中是真命题的为( )
A.,使 B.,使
C., D.,
【例2-2】(2023·山东)已知命题;命题,则下列说法正确的是( )
A.为存在量词命题且为假命题,为全称量词命题且为假命题
B.为全称量词命题且为假命题,为存在量词命题且为假命题
C.为存在量词命题且为真命题,为全称量词命题且为假命题
D.为全称量词命题且为真命题,为存在量词命题且为真命题
【一隅三反】
1.(2023·辽宁)关于命题“,”,下列判断正确的是( )
A.该命题是全称量词命题,且是真命题B.该命题是存在量词命题,且是真命题
C.该命题是全称量词命题,且是假命题D.该命题是存在量词命题,且是假命题
2.(2023·黑龙江)下列四个命题中,既是存在量词命题又是真命题的是( )
A.锐角三角形的内角都是锐角 B.至少有一个实数x,使
C.两个无理数的和必是无理数 D.存在一个负数x,使
3.(2023·河北·模拟预测)命题:,,命题:,,则( )
A.真真B.假假C.假真D.真假
考点三 命题的否定
【例3-1】(2023春·河南)命题“”的否定是( )
A.B.
C.D.
【例3-2】(2023春·陕西商洛)命题,则是( )
A.B.
C.D.
【一隅三反】
1.(2023春·辽宁)若命题:,,则命题的否定为( )
A.,B.,
C.,D.,
2.(2023·广西河池)命题“”的否定是( )
A.B.
C.D.
3.(2022秋·广西柳州)已知命题的否定为“,”,则下列说法中正确的是( )
A.命题为“,”且为真命题
B.命题为“,”且为假命题
C.命题为“,”且为假命题
D.命题为“,”且为真命题
考点四 根据命题真假求参数
【例4-1】(2023春·四川宜宾)已知命题p:为真命题,则实数a的值不能是( )
A.1B.2C.3D.
【例4-2】(2022秋·福建龙岩)已知命题:,,若是真命题,则实数的取值范围是( )
A.B.C.D.
【例4-3】(2023·山西晋城)已知命题,,若命题p是假命题,则a的取值范围为( )
A.B.
C.D.
【一隅三反】
1.(2023河北)命题“”为真命题的一个充分不必要条件是( )
A.B.
C.D.
2.(2023·重庆北碚)已知命题“,”为假命题,则实数的取值范围是( )
A.或B.
C.或D.
3.(2023河南)命题“,使”是假命题,则实数的取值范围为 _____.
4.(2023·福建厦门)命题“”为假命题的一个必要不充分条件是( )
A.B.
C.D.
全称
量词
定义
短语“所有的”“任意一个”在逻辑中通常叫做全称量词
符号表示
∀
全称量
词命题
定义
含有全称量词的命题,叫做全称量词命题
一般形式
对M中任意一个x,p(x)成立(说明:M表示变量x的取值范围)
符号表示
∀x∈M,p(x)
定义
短语“存在一个”“至少有一个”在逻辑中通常叫做存在量词
存在量词
符号表示
∃
存在量词命题
定义
含有存在量词的命题,叫做存在量词命题
一般形式
存在M中的元素x,p(x)成立(说明:M表示变量x的取值范围)
符号表示
∃x∈M,p(x)
命题类型
全称量词命题
存在量词命题
形式
∀x∈M,p(x)
∃x∈M,p(x)
否定形式
∃x∈M,
∀x∈M,
结论
全称量词命题的否定是存在量词命题;
存在量词命题的否定是全称量词命题
正面词语
等于
大于(>)
小于(<)
是
都是
否定
不等于
不大于(≤)
不小于(≥)
不是
不都是
正面词语
至少有一个
至多有一个
任意的
所有的
至多有n个
否定
一个也没有
至少有两个
某个
某些
至少有n+1个
高中人教A版 (2019)1.4.2 充要条件练习题: 这是一份高中人教A版 (2019)<a href="/sx/tb_c4053111_t7/?tag_id=28" target="_blank">1.4.2 充要条件练习题</a>,文件包含人教版高中数学必修一精讲精练14充分必要条件精讲原卷版docx、人教版高中数学必修一精讲精练14充分必要条件精讲解析版docx等2份试卷配套教学资源,其中试卷共24页, 欢迎下载使用。
高中数学人教A版 (2019)必修 第一册5.3 诱导公式优秀测试题: 这是一份高中数学人教A版 (2019)必修 第一册<a href="/sx/tb_c4000282_t7/?tag_id=28" target="_blank">5.3 诱导公式优秀测试题</a>,文件包含人教版高中数学必修一精讲精练53诱导公式精讲原卷版docx、人教版高中数学必修一精讲精练53诱导公式精讲解析版docx等2份试卷配套教学资源,其中试卷共18页, 欢迎下载使用。
高中数学人教A版 (2019)必修 第一册4.5 函数的应用(二)精品同步测试题: 这是一份高中数学人教A版 (2019)必修 第一册<a href="/sx/tb_c4000277_t7/?tag_id=28" target="_blank">4.5 函数的应用(二)精品同步测试题</a>,文件包含人教版高中数学必修一精讲精练45函数的应用二精讲原卷版docx、人教版高中数学必修一精讲精练45函数的应用二精讲解析版docx等2份试卷配套教学资源,其中试卷共34页, 欢迎下载使用。













