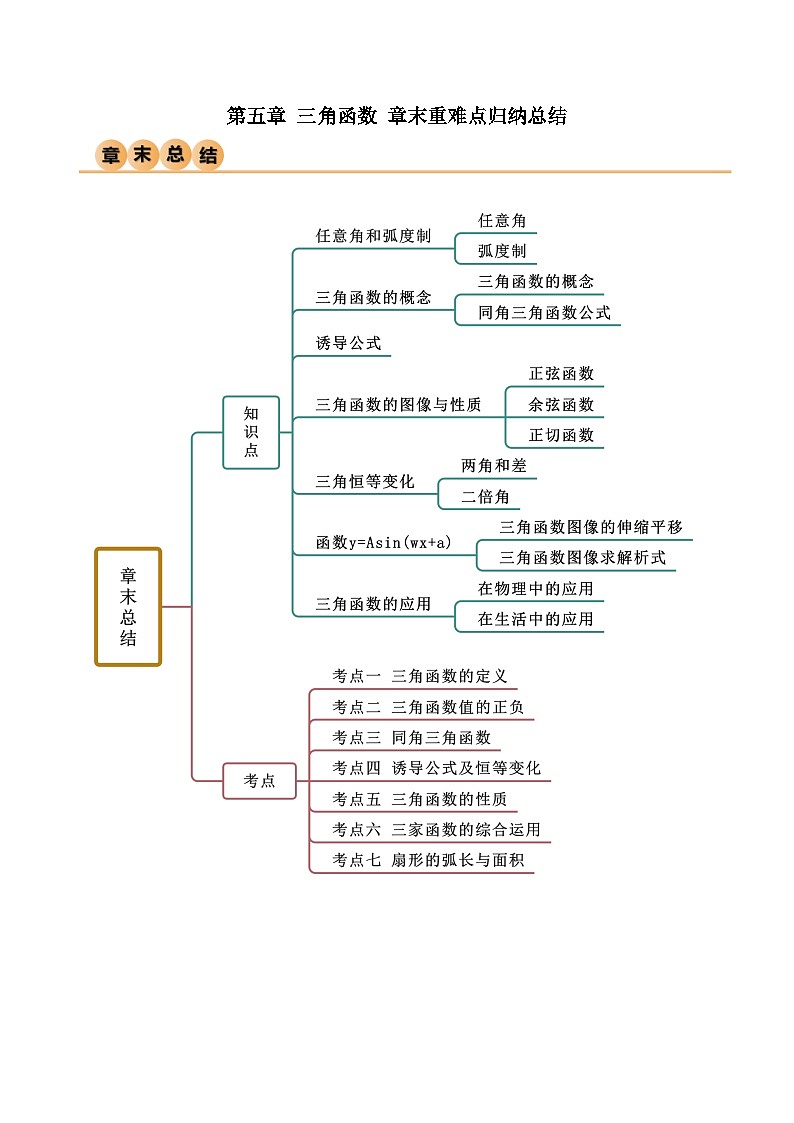
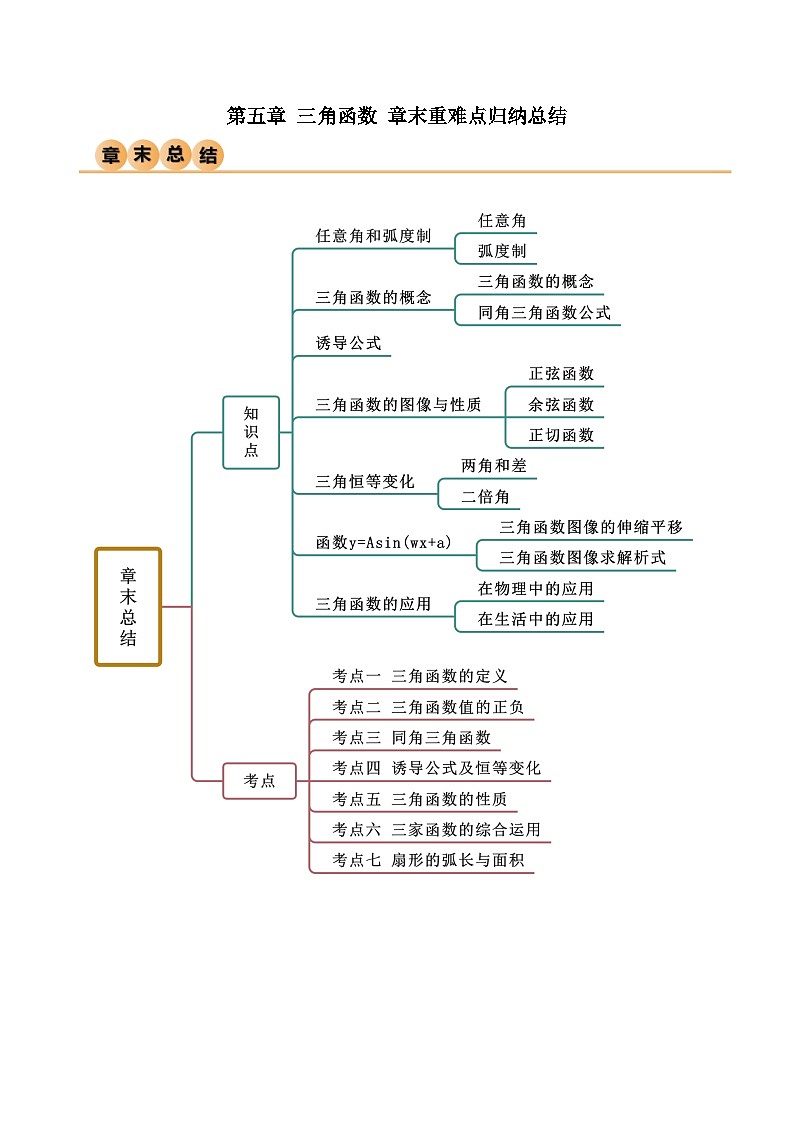
人教版高中数学必修一 精讲精练第五章 三角函数 章末重难点归纳总结（2份，原卷版+解析版）

这是一份人教版高中数学必修一 精讲精练第五章 三角函数 章末重难点归纳总结（2份，原卷版+解析版），文件包含人教版高中数学必修一精讲精练第五章三角函数章末重难点归纳总结原卷版docx、人教版高中数学必修一精讲精练第五章三角函数章末重难点归纳总结解析版docx等2份试卷配套教学资源，其中试卷共41页， 欢迎下载使用。

第五章 三角函数 章末重难点归纳总结考点一 三角函数的定义【例1】（2023秋·江苏盐城·高一校联考期末）已知角终边经过点，且，则的值为（    ）A． B． C． D．【答案】C【解析】因为角终边经过点，所以，所以，解得.故选：C【一隅三反】1．（2023春·广西钦州·高一统考期末）（多选）已知角的顶点为坐标原点，始边与x轴的非负半轴重合，终边上存两点，且，则（    ）A． B．C． D．【答案】BCD【解析】因为角的顶点为坐标原点，始边与x轴的非负半轴重合，终边上存两点，且，所以， 所以，由，可知，所以角为第二象限的角，所以，所以，所以A错误，B正确，所以，，所以CD正确，故选：BCD2．（2023·上海）（多选）在平面直角坐标系中，角的顶点与坐标原点重合，始边与轴的非负半轴重合，终边经过点，且，则的值可以是（    ）A． B．1 C．0 D．2【答案】BC【解析】由题设，故，整理得，所以或.故选：BC3．（2023春·黑龙江大庆·高一大庆实验中学校考阶段练习）（多选）设角终边上的点的坐标为，则（    ）A． B． C． D．【答案】BC【解析】因为角终边上的点的坐标为，所以，故A错误C正确；，故B正确；，故D错误.故选：BC.4（2022秋·浙江绍兴·高一统考期末）（多选）已知角的终边上有一点的坐标是，其中，则下列取值有可能的是（    ）A． B．C． D．【答案】BCD【解析】当时，，则，，则，，故D正确；当时，，则，，则，，故BC正确；综上，A错误，BCD可能正确.故选：BCD.考点二 三角函数值的正负【例2-1】（2023春·云南怒江·高一校考期中）（多选）若，则角的终边位于（    ）A．第一象限 B．第二象限C．第三象限 D．第四象限【答案】BC【解析】因为，则或，若，，此时的终边位于第三象限，若，，此时的终边位于第二象限，综上可得的终边位于第二象限或第三象限.故选：BC．【例2-2】（2023·广东湛江）若，则可能在的象限是（   ）A．第一象限 B．第二象限 C．第三象限 D．第四象限【答案】BCD【解析】当是第一象限角时，，故一定不是第一象限角；当是第二象限角时，，即可以是第二象限角；当是第三象限角时，，即可以是第三象限角；当是第四象限角时，，即可以是第四象限角．故选：BCD.【一隅三反】1．（2022秋·山西·高一校联考阶段练习）（多选）已知是第三象限角，则下列结论中正确的是（    ）A． B．C． D．【答案】AD【解析】已知是第三象限角，∴.对于AB，由，角的终边在一、二象限或y轴非负半轴上，成立，A正确；不一定成立，B错误；对于CD，由，角的终边在第二象限或第四象限，不一定成立，C错误；成立， D正确.故选：AD．2．（2023秋·高一课时练习）（多选）在平面直角坐标系中，角顶点在原点，以正半轴为始边，终边经过点，则下列各式的值恒大于0的是（    ）A． B．C． D．【答案】AB【解析】由题意知角在第四象限，所以，，.选项A，；选项B，；选项C，；选项D，符号不确定.故选：AB.3．（2023春·陕西渭南·高一校考期中）(多选)下列各三角函数值符号为负的有（    ）A． B．C． D．【答案】BD【解析】选项A，因为角是第一象限角，所以，故选项A不满足题设条件；选项B，因为角是第二象限角，所以，故选项B满足题设条件；选项C，因为，所以角是第二象限角，所以，故选项C不满足题设条件；选项D，因为，故选项D满足题设条件；故选：BD.考点三 同角三角函数【例3-1】（2022春·高一课时练习）（多选）下列说法中正确的有（    ）A．若，则B．已知角，若，则C．已知角，若，则D．对于任意角都有【答案】AC【解析】对A，因为，所以，正确；对B，，，的值为负数，不正确；对C，，在第一象限，则，正确；对D，当时，，不存在，故不正确.故选：AC.【例3-2】（2023春·贵州遵义·高一遵义二十一中校考阶段练习）已知，则下列结果正确的是（    ）A． B．C． D．【答案】ABC【解析】，故A正确；，故B正确；，故C正确；，故D错误.故选：ABC.【例3-3】（2023·天津）已知，，则下列选项中正确的有（    ）A． B．C． D．【答案】ACD【解析】将两边同时平方，整理得，所以，故D正确．又，所以，所以由，解得，故C正确，所以，，故A正确，B错误，故选：ACD．【一隅三反】1．（2023·湖北）（多选）已知，且，则关于表述正确的是（    ）A． B． C． D．【答案】AD【解析】因为，且，所以，则，，，故选：AD2．（2023·全国·高一假期作业）（多选）已知，则下列选项正确的是(    )A． B．C． D．【答案】ABD【解析】两边平方，得，即，则，选项A正确；因为，所以，又因为，所以，因为，所以，选项B正确，因为，故D正确， C错误，故选：ABD．3．（2023·全国·高一假期作业）（多选）已知,且和是方程的两个实数根,则=（    ）A． B． C． D．【答案】AB【解析】解方程得或;分子分母同时除以得;当时,,当时,.故选：.4．（2023春·吉林·高一东北师大附中校考阶段练习）（多选）已知，，则的可能取值为（    ）A． B． C． D．【答案】AB【解析】由可得，即，即,,,当时，；当时，.故选：AB.考点四 诱导公式及恒等变化【例4-1】（2023秋·山东德州·高三德州市第一中学校考开学考试）已知是第四象限角，.(1)化简；(2)若，求的值.【答案】(1)(2)【解析】（1）.（2），即，又是第四象限角，，.【例4-2】（2023春·四川达州·高一四川省万源中学校考阶段练习）化简的值为（    ）A．1 B． C． D．2【答案】A【解析】故选：A.【例4-3】（2023秋·四川眉山 ）已知，则（    ）A． B． C． D．【答案】D【解析】因为，即，所以．故选：D【例4-4】（2023春·江苏镇江·高一统考阶段练习）（多选）已知，，其中，则（    ）A． B．C． D．【答案】ACD【解析】，∴，∴A正确；∴，∴B错误；，，∴，∴∴D正确；∴C正确.故选:ACD.【一隅三反】1．（2023秋·四川成都 ）的值为（    ）A． B． C． D．【答案】C【解析】由题意得：，故选：2．（2023·陕西商洛 ）已知，则（    ）A． B． C． D．【答案】D【解析】由，设，①，又②，所以联立①②，解得，故．故选：D3．（2023春·辽宁铁岭·高一西丰县高级中学校考期中） .【答案】【解析】，，所以.故答案为：.4．（2023秋·江西抚州 ）已知.(1)若，求的值；(2)若，求的值.【答案】(1)(2)【解析】（1），由，得，所以；（2）由，得，则.5．（2023春·江苏·高一校考开学考试）给出下列三个条件：①角的终边经过点；②；③．请从这三个条件中任选一个，解答下列问题：(1)若为第四象限角，求的值；(2)求的值．【答案】(1)-2(2)6【解析】（1）选①，方法一：角的终边经过点，因为为第四象限角，故m＞0，点P到原点的距离为，所以，，故．方法二：角的终边经过点，所以，所以，解得，又为第四象限角，所以，，故．选②，由得，所以，解得，又为第四象限角，所以，，故．选③，由得，因为，，所以，故，所以，解得，又为第四象限角，所以，，故．（2）方法一：由（1）得：，所以．方法二：（*），由（1）得：，所以为第二或第四象限角，①若为第二象限角，则，，所以，*式．②若为第四象限角，则，，所以，*式．考点五 三角函数的性质【例5】（2023秋·广西贵港）（多选）已知直线是函数图象的一条对称轴，则（    ）A． B．的图象关于点对称C．的图象关于直线对称 D．在上单调递减【答案】BCD【解析】因为直线是图象的一条对称轴，所以，．又，所以．A不正确．当时，，所以的图象关于点对称．B正确．因为，所以C正确．当时，，单调递减．D正确．故选：BCD【一隅三反】1.（2023云南）（多选）的部分图象如图所示，则（    ）  A．的最小正周期为B．C．的图象关于直线对称D．将的图象向右平移个单位长度得到的函数图象关于y轴对称【答案】AC【解析】由函数的图象，可得，所以，可得，所以，因为，所以，即，可得，即，因为，可得，所以，所以A正确，B不正确；由，所以是函数的图象的对称轴，所以C正确；将的图象向右平移个单位长度，可得，此时函数的图象关于原点对称，不关于轴对称，所以D错误.故选：AC.2．（2023春·云南曲靖·高一校考阶段练习）（多选）将函数的图象向右平移个单位长度后得到函数的图象，且，则下列说法正确的是（    ）A．为奇函数B．C．当时，在上有3个零点D．若在上单调递增，则的最大值为5【答案】BD【解析】∵，∴，且，∴，即为奇数，∴为偶函数，故A错.由上得：为奇数，∴，故B对.由上得，当时，，，由图象可知在上有5个零点，故C错误，    ∵在上单调递增，所以,解得：，又∵，∴的最大值为5，当时，满足在上单调递增，故D对.故选：BD.3．（2024·黑龙江大庆·统考模拟预测）（多选）已知函数的部分图象如图所示，则（    ）  A．B．C．在上单调递增D．的图象关于直线对称【答案】ABD【解析】由图可知，则，故A正确.因为，所以，即.因为，所以，则B正确.令，解得，此时单调递增；令，解得，此时单调递减.由，得在上单调递减，在上单调递增，则C错误.因为，所以.令，，得，.当时，，则的图象关于直线对称，故D正确.故选：ABD.考点六 三家函数的综合运用【例6】（2023秋·湖南常德）已知函数.(1)当时，求的最大值和最小值，以及相应的值；(2)若，，求的值.【答案】(1)，，时，.(2)【解析】（1）∵，∴，当即时，，此时当即时，，此时.（2）∵，∴，∵，∴，∴，【一隅三反】1．（2023秋·山东烟台 ）已知函数，．(1)若函数的图象关于直线对称，求的最小值；(2)若函数在上有零点，求实数的取值范围．【答案】(1)(2)．【解析】（1），由，，解得，，即函数的对称轴为，．∵的图象关于直线对称，∴当时，有最小值．（2）若函数在上有零点，即在上有解，即在上有解，当，，即，，由，解得，故实数的取值范围是．2．（2023春·四川宜宾·高一校考阶段练习）已知函数，将的图象各点横坐标缩短到原来的，纵坐标伸长到原来的2倍，然后再将所得函数图象向左平移个单位后得到函数的图象.(1)求的解析式；(2)方程在上有且只有两个解，求实数n的取值范围；(3)实数m满足对任意，都存在，使得成立，求m的取值范围.【答案】(1)(2)(3)【解析】（1）已知函数，将的图象各点横坐标缩短到原来的，纵坐标伸长到原来的2倍，可得函数的图象，再将所得函数图象向左平移个单位后可得到函数.∴的解析式为.（2）方程在上有且只有两个解，转化为函数与函数在上有且只有两个交点.在上的图象如图所示，    则在单调递增且取值范围是，在单调递减且取值范围是，由图象可知，函数与函数有且只有两个交点，所以，解得，即实数的取值范围为.（3）由（1）知.实数m满足对任意，都存在，使成立，所以对任意，恒成立，即对任意，恒成立，令，设，则，∵，且为增函数，∴，可得在上恒成立.令，，则的最大值，又因为的开口向上，，所以，所以，解得，综述，m的取值范围是.3．（2023春·黑龙江大庆·高一大庆中学校考阶段练习）已知函数的部分图象如图所示.  (1)求函数的解析式及对称中心；(2)若先将函数图象上所有点的横坐标伸长到原来的4倍（纵坐标不变），得到函数的图象；再把图象上所有点向左平行移动个单位长度，得到函数的图象.求函数在上的值域.【答案】(1)；，(2)【解析】（1）由的部分图象可知，，可得，所以，，所以，由于，所以，所以函数的解析式为.，∴，故对称中心为，.（2）若先将函数图象上所有点的横坐标伸长到原来的4倍（纵坐标不变），得到函数的图象，再把后者图象上所有点向左平行移动个单位长度，得到函数的图象.当时，，，所以.所以函数在区间上的值域为.4．（2023春·辽宁大连·高一大连八中校考阶段练习）已知函数(，).从下列四个条件中选择两个作为已知，使函数存在且唯一确定.条件①：；          条件②：为偶函数；条件③：的最大值为1；  条件④：图像的相邻两条对称轴之间的距离为.(1)求的解析式；(2)将函数图像上各点横坐标缩短到原来的一半（纵坐标不变），再将所得图像向左平移个单位，得到函数的图像，若，求；(3)若是函数的一个零点，求的最小值.注：如果选择的条件不符合要求，第（1）问得0分；如果选择多个符合要求的条件分别解答，按第一个解答计分．【答案】(1)选择条件①④，；选择条件③④：(2)(3)【解析】（1）因为，不是函数的最值，所以函数不是偶函数，故不能选择条件②，选择条件①④： 因为函数图像的相邻两条对称轴之间的距离为，所以. . 因为，所以.故. 选择条件③④： 因为函数图像的相邻两条对称轴之间的距离为，所以. . 因为函数的最大值为1，所以. 故;选择条件①③条件③能确定，条件①，得，且，不能确定的值，所以也不能确定函数的解析式.（2）由已知，，即，所以．（3）因为是函数的一个零点，由，可得，即，即，可得或，即或，又因为，所以的最小值为.考点七 扇形的弧长与面积【例7】（2023·江苏 ）《九章算术》是中国古代第一部数学专著，成于公元一世纪左右，系统总结了战国、秦、汉时期的数学成就，其中《方田》一章中记载了计算弧田（弧田就是由圆弧和其所对弦所围成弓形）的面积所用的经验公式：弧田面积=（弦矢+矢矢），公式中“弦”指圆弧所对弦长，“矢”等于半径长与圆心到弦的距离之差，按照上述经验公式计算所得弧田面积与其实际面积之间存在误差，现有圆心角为，弦长为米的弧田，其实际面积与按照上述经验公式计算出弧田的面积之间的误差为（    ）平方米（其中，）A．14 B．16 C．18 D．20【答案】B【解析】如图所示，扇形的半径为，所以扇形的面积为，又三角形的面积为，所以弧田的面积为，又圆心到弦的距离等于，所示矢长为，按照上述弧田的面积经验计算可得弦矢矢，所以两者的差为.故选：B.【一隅三反】1．（2023·全国·高三专题练习）月牙泉，古称沙井，俗名药泉，自汉朝起即为“敦煌八景” 之一，得名“月泉晓澈”，因其形酷似一弯新月而得名，如图所示，月牙泉边缘都是圆弧，两段圆弧可以看成是的外接圆和以为直径的圆的一部分，若，南北距离的长大约m，则该月牙泉的面积约为（    ）（参考数据：）A．572m2 B．1448m2 C．m2 D．2028m2【答案】D【解析】设的外接圆的半径为，则，得，因为月牙内弧所对的圆心角为，所以内弧的弧长，所以弓形的面积为，以为直径的半圆的面积为，所以该月牙泉的面积为，故选：D2．（2023·江苏 ）在中国古代，折扇既实用也是文人雅士或家庭的装饰品，其扇面形状如图实线部分所示.已知该扇面的圆心角为(弧度)，扇面的面积为16，，则扇面的周长(外围实线部分)为A． B．12 C． D．8【答案】C【解析】根据扇形面积公式求解扇形半径，再求扇面周长.【详解】由题意，设， 则周长为故选：C3．（2022·全国·高三专题练习）中国扇文化有着深厚的文化底蕴，文人雅士喜在扇面上写字作画.如图，是书画家唐寅（1470—1523）的一幅书法扇面，其尺寸如图所示，则该扇面所在扇形的圆心角为 rad，此时扇面面积为 cm2．【答案】 704【解析】如图，设，，由题意可得：，解得：，.所以，．故答案为：．