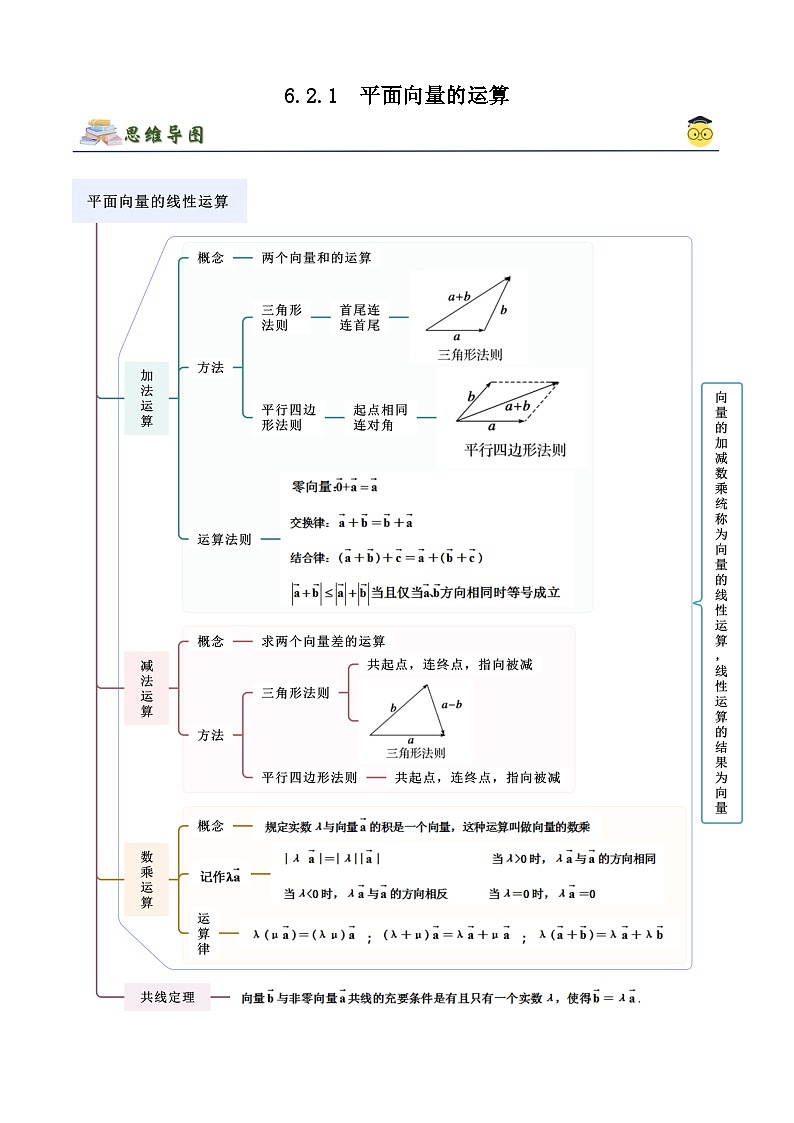
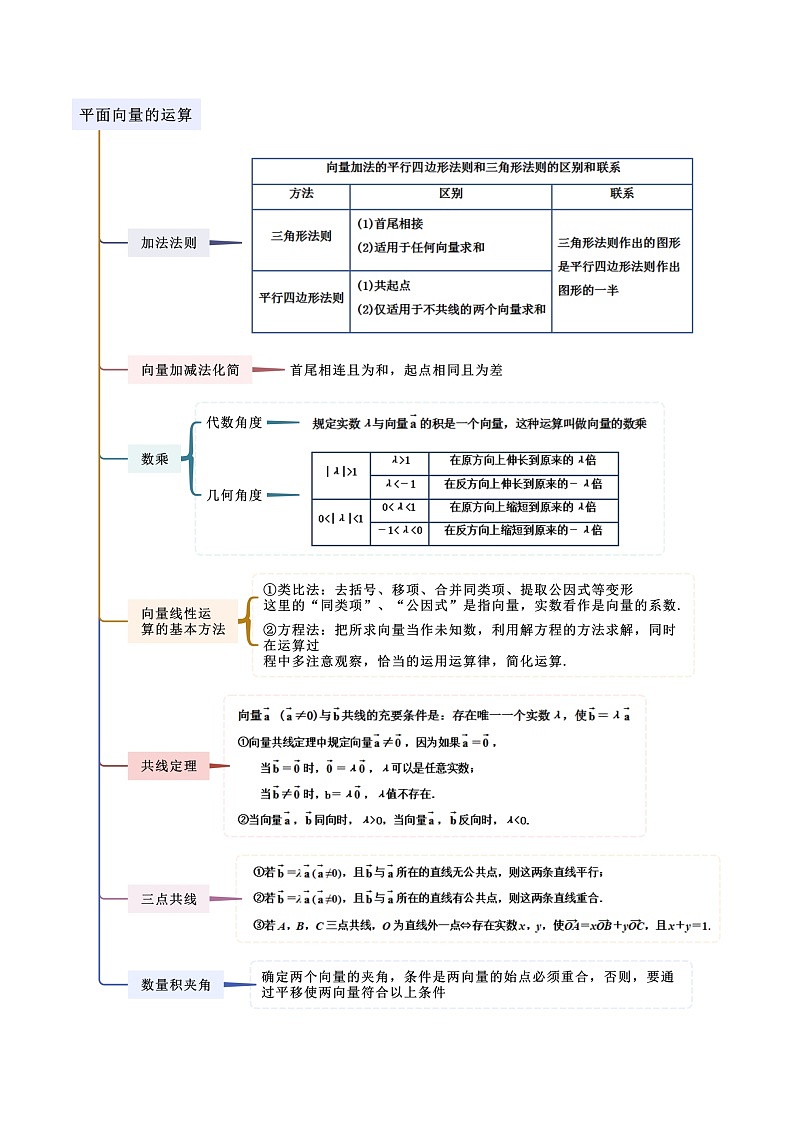
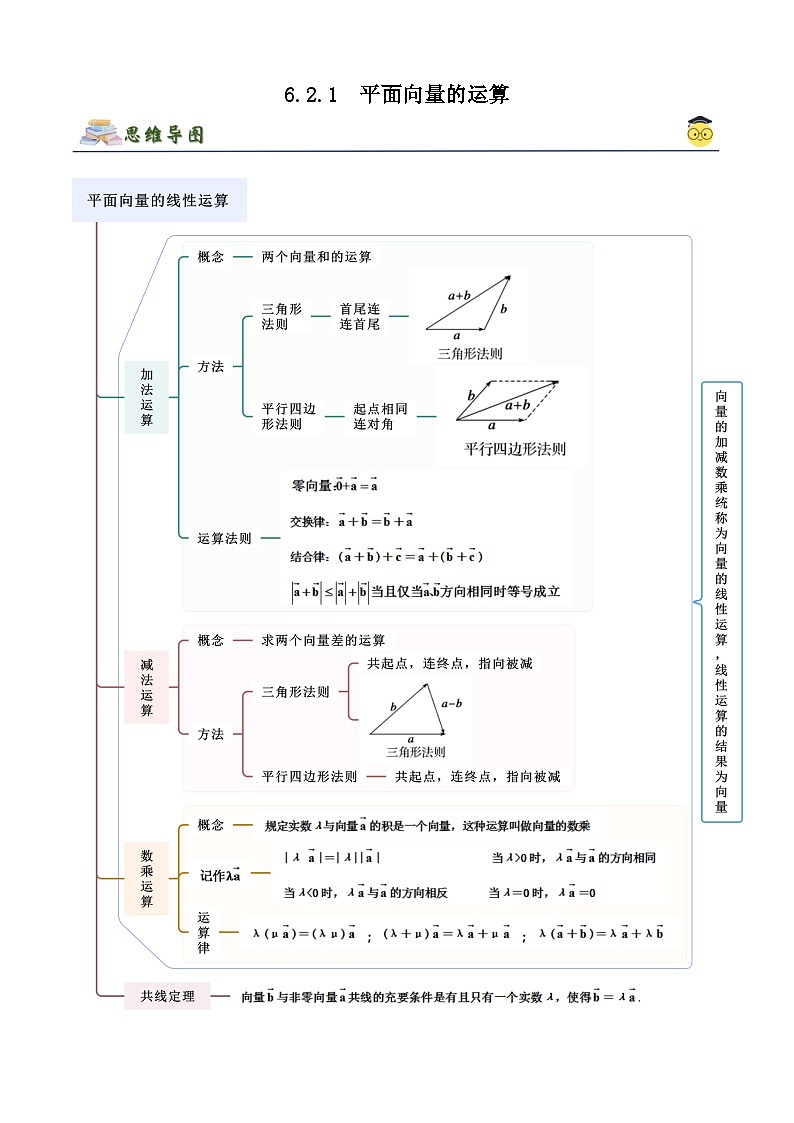
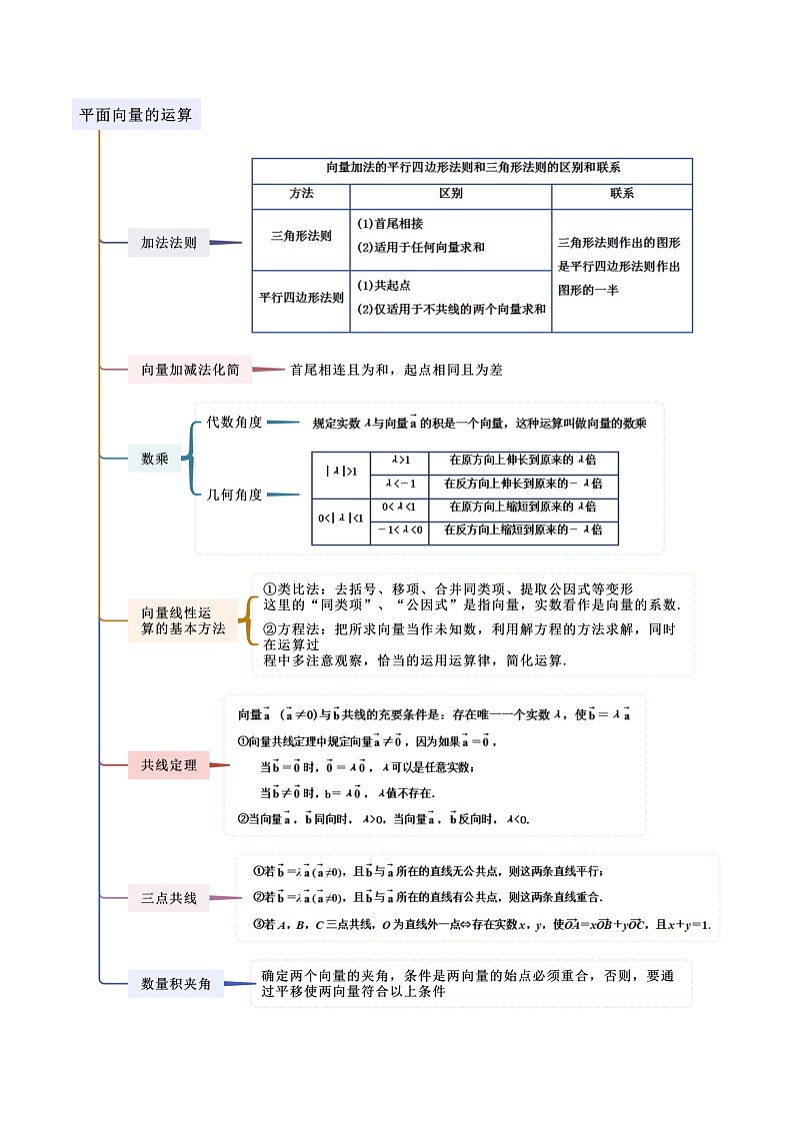
所属成套资源:人教版高中数学必修二 精讲精练 (2份,原卷版+解析版)
高中数学人教A版 (2019)必修 第二册6.2 平面向量的运算精品精练
展开
这是一份高中数学人教A版 (2019)必修 第二册6.2 平面向量的运算精品精练,文件包含人教版高中数学必修二精讲精练621平面向量的运算原卷版docx、人教版高中数学必修二精讲精练621平面向量的运算解析版docx等2份试卷配套教学资源,其中试卷共46页, 欢迎下载使用。
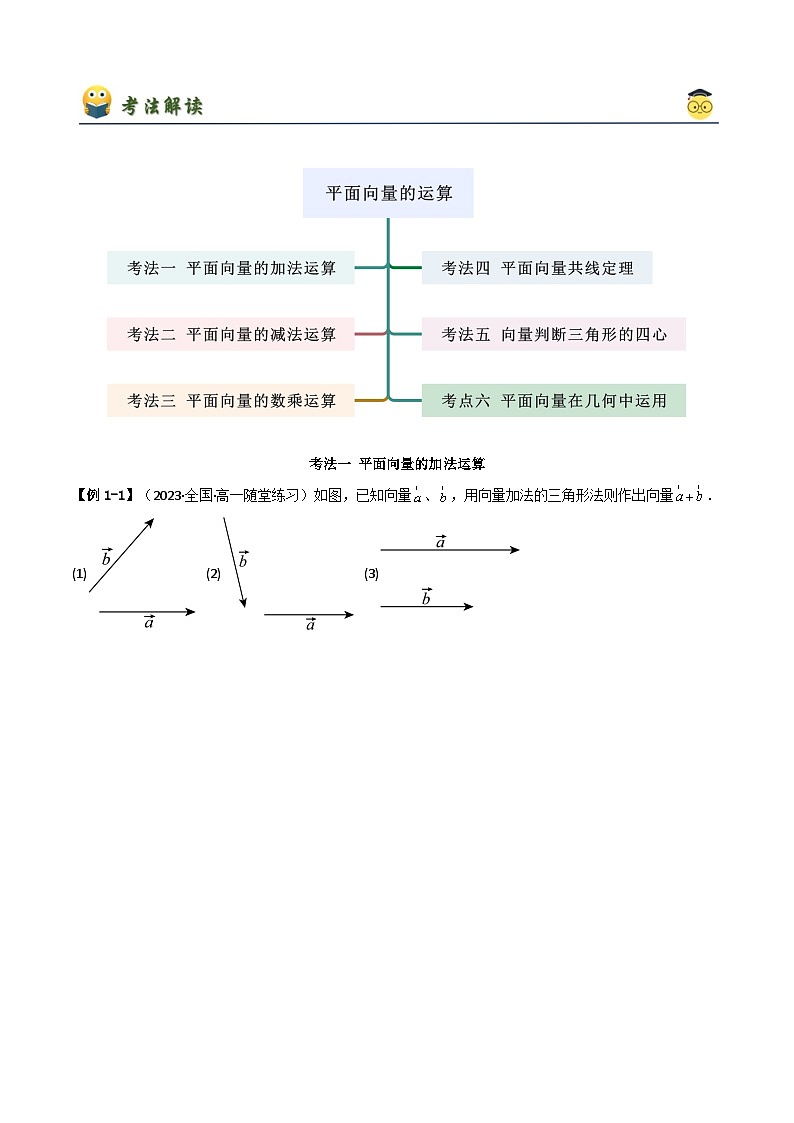
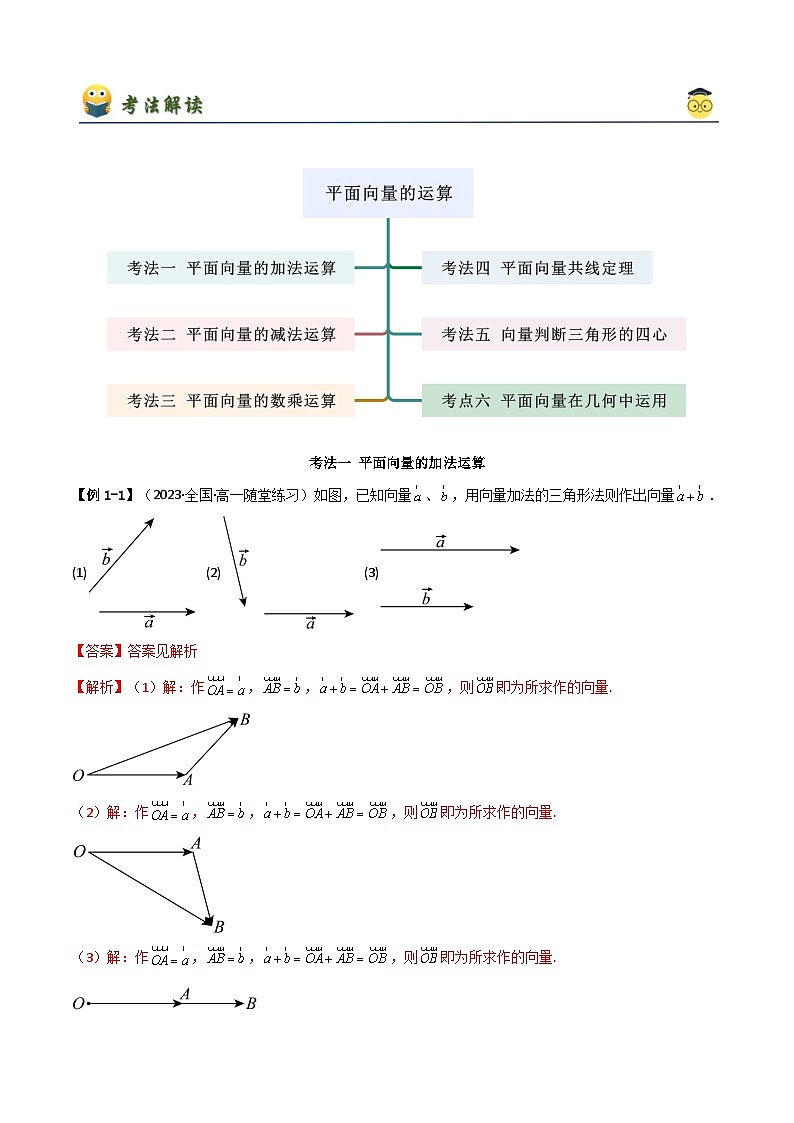
考法一 平面向量的加法运算
【例1-1】(2023·全国·高一随堂练习)如图,已知向量、,用向量加法的三角形法则作出向量.
(1) (2) (3)
【答案】答案见解析
【解析】(1)解:作,,,则即为所求作的向量.
(2)解:作,,,则即为所求作的向量.
(3)解:作,,,则即为所求作的向量.
【例1-2】(2023下·新疆·高一校考期末)化简下列各式:
(1);
(2);
(3);
(4);
(5).
【答案】(1);(2);(3);(4);(5).
【解析】(1);
(2);
(3);
(4);
(5).
【一隅三反】
1.(2023山西)如图所示,求:
(1);
(2);
(3);
(4).
【答案】(1)(2)(3)(4)
【解析】(1);
(2);
(3);
(4).
2.(2023云南)如图,为边长为1的正六边形,O为其几何中心.
(1)化简;
(2)化简;
(3)化简;
(4)求向量的模.
【答案】(1)(2)(3)(4)2
【解析】(1)解:根据向量的平行四边形法则得;
(2)解:根据题意,,所以;
(3)解:因为,所以;
(4)解:因为,所以,
所以
3.(2023·全国·高一随堂练习)如图,已知向量,,不共线,求作向量.
【答案】详见解析
【解析】解法一:(三角形法则),如下图所示,作,,
则,再作,则,即.
解法二:(平行四边形法则)因为向量,,不共线,
如下图所示,在平面内任取一点O,作,,
以,为邻边作平行四边形,则对角线,
再作,以,为邻边作平行四边形,则.
考法二 平面向量的减法运算
【例2-1】(2023·全国·高一随堂练习)如图,已知向量、,求作.
(1) (2) (3) (4)
【答案】答案见解析
【解析】(1)解:作,,则,即即为所求作的向量.
(2)解:作,,则,即即为所求作的向量.
(3)解:作,,则,即即为所求作的向量.
(4)解:作,,则,即即为所求作的向量.
【例2-2】(2023·河南周口)化简下列各式:
(1); (2); (3).
(4); (5); (6).
【答案】(1);(2);(3).(4);(5);(6).
【解析】(1).
(2).
(3).
(4).
(5).
(6).
【一隅三反】
1.(2023下·江苏淮安·高一校考阶段练习)如图,已知向量
(1)用表示;
(2)用表示;
(3)用表示;
(4)用表示;
(5)用表示
【答案】(1)(2)(3)(4)(5)
【解析】(1).
(2).
(3)
(4).
(5)
2(2023·高一课时练习)如图,四边形ABCD中,设,,,试用,,分别表示,.
【答案】,.
【解析】由题图知:,
又,所以.
考法三 平面向量的数乘
【例3】(2023·全国·高一随堂练习)判断下列各小题中的向量,是否共线:
(1),;
(2),(其中两个非零向量和不共线);
(3),.
【答案】(1)共线;(2)共线;(3)共线.
【解析】(1),,所以,所以,共线.
(2),,所以,所以,共线.
(3)因为,,所以,所以.所以,共线.
【一隅三反】
.(2023下·高一课时练习)计算:
(1);
(2).
(3);
(4)
(5);
(6);
(7);
(8).
【答案】(1)(2)(3)(4)(5);(6);
(7);(8).
【解析】(1)原式.
(2)原式
(3)原式=.
(4)原式=
.
(5)
(6)
(7)
(8)
考法四 平面向量共线定理
【例4】(2023新疆)设,是两个不共线的向量,如果,,.
(1)求证:A,B,D三点共线;
(2)试确定的值,使和共线;
(3)若与不共线,试求的取值范围.
【答案】(1)证明过程见解析(2)(3)
【解析】(1)证明:因为,所以与共线.
因为与有公共点B,所以A,B,D三点共线.
(2)因为与共线,所以存在实数,使.
因为,不共线,所以所以.
(3)假设与共线,则存在实数m,使.
因为,不共线,所以所以.因为与不共线,所以.
【一隅三反】
1.(2024上·辽宁·高一校联考期末)已知与为非零向量,,若三点共线,则( )
A.0B.1C.2D.3
【答案】D
【解析】由题意知,三点共线,故,且共线,
故不妨设,则,所以,解得,故选:D
2.(2022·全国·高一课时练习)设两个非零向量与不共线.
(1)若,,,求证:,,三点共线;
(2)试确定实数,使和同向.
【答案】(1)证明见解析;(2).
【解析】(1)证明:因为,,,
所以.所以,共线.
又因为,有公共点,所以,,三点共线.
(2)解:因为与同向,所以存在实数,使,
即.所以.
因为,是不共线的两个非零向量,所以,解得,或,又因为,所以.
3.(2024·上海)设是不共线的两个非零向量.
(1)若,求证:三点共线;
(2)若与共线,求实数的值;
(3)若,且三点共线,求实数的值.
【答案】(1)证明见解析;(2).(3).
【解析】证明:(1),所以.
又因为为公共点,所以三点共线.
(2)设,则
解得或
所以实数的值为.
(3),
因为三点共线,所以与共线.
从而存在实数使,即,
得解得所以.
考法五 向量判断三角形的四心
【例5】(2023·山西太原)已知点在所在平面内,满,,则点依次是的( )
A.重心,外心B.内心,外心C.重心,内心D.垂心,外心
【答案】A
【解析】设中点为,因为, 所以,即,
因为有公共点,所以,三点共线,即在的中线,
同理可得在的三条中线上,即为的重心;
因为,所以,点为的外接圆圆心,即为的外心
综上,点依次是的重心,外心.故选:A
【一隅三反】
1.(2023·重庆江北)(多选)设点M是所在平面内一点,则下列说法正确的是( )
A.若,则点M是BC的中点
B.若,则点M是的重心
C.若,则点M,B,C三点共线
D.若,则
【答案】ACD
【解析】对于A中,如图所示,根据向量的平行四边形法则,可得,
若,可得M为BC的中点,所以A正确;
对于B中,若M为的重心,则满足,
即,所以B不正确;
对于C中,由,可得,即,
所以M,B,C三点共线,所以C正确;
对于D中,如图所示,由,
可得,所以D正确.
故选:ACD
2.(2023·山东枣庄·)(多选)数学家欧拉在1765年发表的《三角形的几何学》一书中提出定理:三角形的外心、重心、垂心依次位于同一条直线上,且重心到外心的距离是重心到垂心距离的一半,此直线被称为三角形的欧拉线,该定理则被称为欧拉线定理.设点O、G、H分别是△ABC的外心、重心、垂心,且M为BC的中点,则( )
A.B.
C.D.
【答案】ABD
【解析】A. 为重心,所以,
所以,
所以,
所以,所以该选项正确.
B.,
由于G是重心,所以,所以,
同理,所以,
所以该选项正确.
C.,所以该选项错误.
D.,
所以,所以该选项正确.
故选:ABD
3.(2023·重庆万州)(多选)已知分别为的外心和重心,为平面内一点,且满足,则下列说法正确的是( )
A.
B.为内心
C.
D.对于平面内任意一点,总有
【答案】ACD
【解析】A:由为的重心,则,,,
所以,即,正确;
B:,由为外心,所以,
即,同理,故为垂心,错误.
C:,所以,
因为,故,而,
所以,即,正确.
D:,所以,
因为,故,正确.
故选:ACD
考法六 平面向量在几何中应用
【例6】(2024北京)如图所示,在△ABC中,D,F分别是BC,AC的中点,.
(1)用表示;
(2)求证:B,E,F三点共线.
【答案】(1),,,,
(2)证明见解析
【解析】(1)解:在△ABC中,D,F分别是BC,AC的中点,
则,
故,,
,;
(2)证明:因为,,所以,
所以,又因有公共点,所以B,E,F三点共线.
【一隅三反】
1.(2023·河北)如图,已知四边形为平行四边形,与相交于,,,设,,试用基底表示向量,,.
【答案】,,
【解析】是平行四边形,,,,
,
,
.
2.(2023下·河南南阳·高一统考阶段练习)如图所示,在平行四边形中,,分别为边和的中点,为与的交点.
(1)若,则四边形是什么特殊的平行四边形?说明理由.
(2)化简,并在图中作出表示该化简结果的向量.
【答案】(1)菱形,理由见解析
(2)答案见解析
【解析】(1)由条件知,
即,又四边形是平行四边形,故四边形是菱形.
(2)由平行四边形及三角形中位线的性质可知.
所以.
作出向量如图所示.
单选题
1.(2023吉林)向量化简后等于( )
A.B.C.D.
【答案】C
【解析】
故选:C.
2(2023·安徽)如图,D、E、F分别是△ABC的边AB、BC、CA的中点,则下列等式中错误的是( )
A.++=0B.++=0
C.++=D.++=
【答案】D
【解析】++=+=0,A正确;
++=++=0,B正确;
++=+=+=,C正确;
++=+0==≠,D错误,
故选:D.
3.(2023广西)作用在同一物体上的两个力,当它们的夹角为时,则这两个力的合力大小为( )N.
A.30B.60C.90D.120
【答案】B
【解析】如图,,,,作平行四边形,则,
因为,所以四边形是菱形,又,是等边三角形,.
故选:B.
4.(2013北京)若是内一点,,则是的( )
A.内心B.外心C.垂心D.重心
【答案】D
【解析】取线段的中点,连接,则,而,
因此,即三点共线,线段是的中线,且是靠近中点的三等分点,
所以是的重心.
故选:D
5.(2023湖北)设是两个不共线的向量,若向量与共线,则( )
A.λ=0B.λ=-1
C.λ=-2D.λ=-
【答案】D
【解析】由已知得存在实数k使,即,于是1=2k且λ=-k,解得λ=-.
6.(2024·山东)已知△ABC,点G、M满足,,则( )
A.B.
C.D.
【答案】A
【解析】满足,∴为的重心,
∴==,
又∵,
∴
.
故选:A.
7.(2023·全国·专题练习)设为的外心,若,则点是的( )
A.重心B.内心C.垂心D.外心
【答案】C
【解析】取BC的中点D,如图所示,
连接OD,AM,BM,CM.
因为,
所以,
又,则,
所以,
又由于为的外心,
所以,
因此有.同理可得,,
所以点是的垂心.
故选:C.
8.(2023甘肃省)已知是的边的中点,点在上,且满足,则与的面积之比为( )
A.B.C.D.
【答案】C
【解析】如图,由得,
即,即,故,
故与以为底,其高的比为,故.
故选:C.
多选题
9.(2023下·陕西西安·高一期中)下列命题正确的的有( )
A.
B.
C.若,则共线
D.,则共线
【答案】ABC
【解析】对于A,,故正确;
对于B,,故正确;
对于C,因为,所以,所以共线,故正确;
对于D,因为恒成立,所以不一定共线,故错误.
故选:ABC.
10.(2023下·陕西西安·高一阶段练习)下列说法不正确的是( )
A.已知均为非零向量,则 存在唯一的实数,使得
B.若向量共线,则点必在同一直线上
C.若且,则
D.若点为的重心,则
【答案】BC
【解析】由平行向量的基本定理可知,选项A是正确的;
向量共线的意思是向量所在的基线平行或共线,
只有当向量,所在的直线线共线时,点,,,才在同一直线上,故B不正确;
由平面向量的数量积可知,若,则,
所以,无法得到,故C不正确;
设线段的中点为,若点为的重心,
则,而,所以,即D正确.
故选:BC.
11.(2023上·辽宁·高一沈阳二中校联考期末)《易经》是中华民族智慧的结晶,易有太极,太极生二仪,二仪生四象,四象生八卦,其中八卦深邃的哲理解释了自然、社会现象.如图1所示的是八卦模型图,其平面图形如图2中的正八边形,其中O为正八边形的中心,则下列说法正确的是( )
A.B.
C.D.和不能构成一组基底
【答案】BCD
【解析】因为正八边形中,,所以,但方向不同,所以不正确,故A错误;
由,所以正确,故B正确;
由正八边形知,,且,
根据向量加法法则可知:
为以为邻边的正方形中以为始点的一条对角线所对应的向量,
所以,又,
与以为始点的一条对角线所对应的向量共线,所以,故C正确;
在正八边形中,,和平行,所以和共线,故和不能构成一组基底,故D正确.
故选:BCD
12.(2023下·广东·高一校联考期中)设点是所在平面内一点,则下列说法正确的是( )
A.若,则的形状为等边三角形
B.若,则点三点共线
C.若点是的重心,则
D.若所在平面内一动点满足:,则的轨迹一定通过的内心
【答案】ACD
【解析】对于A,,为等边三角形,故A正确;
对于B,,,、、三点不共线,故B错误;
对于C,设,,分别为,,的中点,则,
,,
,即,故C正确;
对于D,,,,,在的角平分线上,的轨迹一定通过的内心,故D正确.
故选:ACD.
填空题
13.(2024·全国·高一课时练习)( )
A.B.C.D.
【答案】A
【解析】由向量的运算法则,可得.
故选:A.
14.(2024上·辽宁大连·高一期末)设,是两个不共线的向量,向量,共线,则 .
【答案】
【解析】与共线,,,
又,是两个不共线的向量,,解得.
故答案为:.
15.(2023上·湖南邵阳)如图,在平行四边形ABCD中,E是对角线AC上靠近点的三等分点,点F为BE的中点,若,则 .
【答案】
【解析】
,
所以,,.故答案为:.
16.(2022·高一课时练习)若向量,,则 .
【答案】
【解析】;
;
;
.
故答案为:.
解答题
17.(2023·高一课前预习)计算:
(1);
(2);
(3);
(4).
【答案】(1)
(2)
(3)
(4)
【解析】(1)
;
(2)
;
(3)
;
(4)
.
18.(2024湖南)如图,按下列要求作答.
(1)以A为始点,作出;
(2)以B为始点,作出;
(3)若为单位向量,求、和.
【答案】(1)作图见解析
(2)作图见解析
(3),,
【解析】(1)将的起点同时平移到A点,利用平行四边形法则作出,如下图所示:
(2)先将共线向量的起点同时平移到B点,计算出,再将向量与之首尾相接,利用三角形法则即可作出,如下图所示:
(3)由是单位向量可知,根据作出的向量利用勾股定理可知,
;
由共线向量的加法运算可知;
19.(2023·全国·高一课堂例题)如图,中,AB边的中点为P,重心为G.在外任取一点O,作向量,,,,.
(1)试用,表示.
(2)试用,,表示.
【答案】(1)
(2)
【解析】1)
.
(2)
.
20.(2023下·河南周口·高一太康县第一高级中学校考阶段练习)如图所示平行四边形中,设向量,,又,,用,表示、、.
【答案】,,
【解析】∵,
∴;
又,;
∴.
21.(2023·全国·高一随堂练习)如图,点D是中BC边的中点,,.
(1)试用,表示;
(2)若点G是的重心,能否用,表示?
(3)若点G是的重心,求.
【答案】(1)
(2)
(3)
【解析】(1)因为点D是中BC边的中点,且,,
所以;
(2)因为点G是的重心,
所以
.
(3)因为点G是的重心且D是BC边的中点,所以,
又,所以,所以.
22.(2023江苏)如图,在平行四边形中,设, , 则
(1)当,满足什么条件时,与垂直?
(2)当,满足什么条件时,?
(3)与可能是相等向量吗?
(4)当,满足什么条件时,平分与所夹的角?
【答案】(1)
(2)
(3)不可能相等
(4)
【解析】由向量加减法的几何意义可知,,,
当时,,即平行四边形的相邻边长相等,故平行四边形为菱形,而菱形的对角线与互相垂直,所以与互相垂直,
故.
(2)当时,,即平行四边形的对角线长相等,此时平行四边形为矩形,所以,即时,.
(3)不可能相等,
因为平行四边形的对角线方向不同,所以与的方向一定不同,故不可能是相等向量.
(4)当时,由(1)可知平行四边形为菱形,而菱形的对角线会平分,即会平分与所夹的角,
故.
相关试卷
这是一份人教A版 (2019)必修 第二册6.4 平面向量的应用课时作业,文件包含人教版高中数学必修二精讲精练641正余弦定理原卷版docx、人教版高中数学必修二精讲精练641正余弦定理解析版docx等2份试卷配套教学资源,其中试卷共52页, 欢迎下载使用。
这是一份高中数学人教A版 (2019)必修 第二册6.2 平面向量的运算练习题,文件包含人教版高中数学必修二精讲精练622向量的数量积原卷版docx、人教版高中数学必修二精讲精练622向量的数量积解析版docx等2份试卷配套教学资源,其中试卷共34页, 欢迎下载使用。
这是一份高中数学人教A版 (2019)选择性必修 第一册1.1 空间向量及其运算课后测评,文件包含人教版高中数学选择性必修一精讲精练11空间向量及运算精讲原卷版docx、人教版高中数学选择性必修一精讲精练11空间向量及运算精讲解析版docx等2份试卷配套教学资源,其中试卷共28页, 欢迎下载使用。










