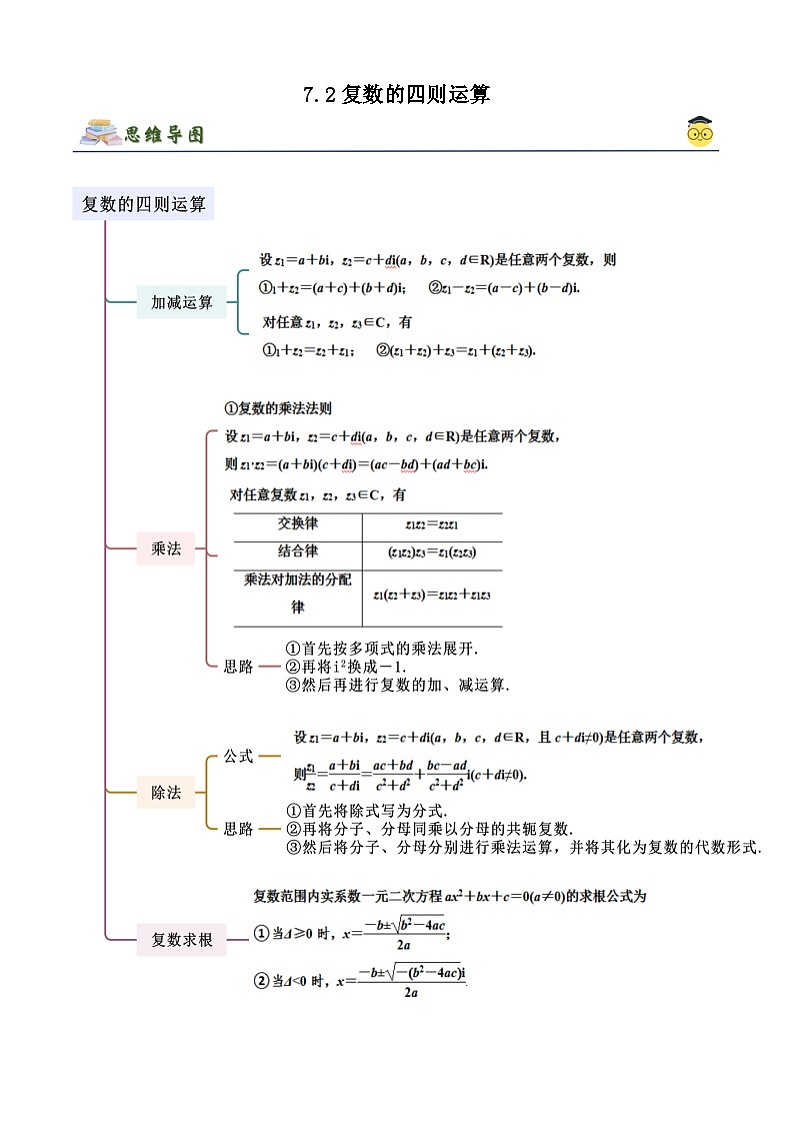
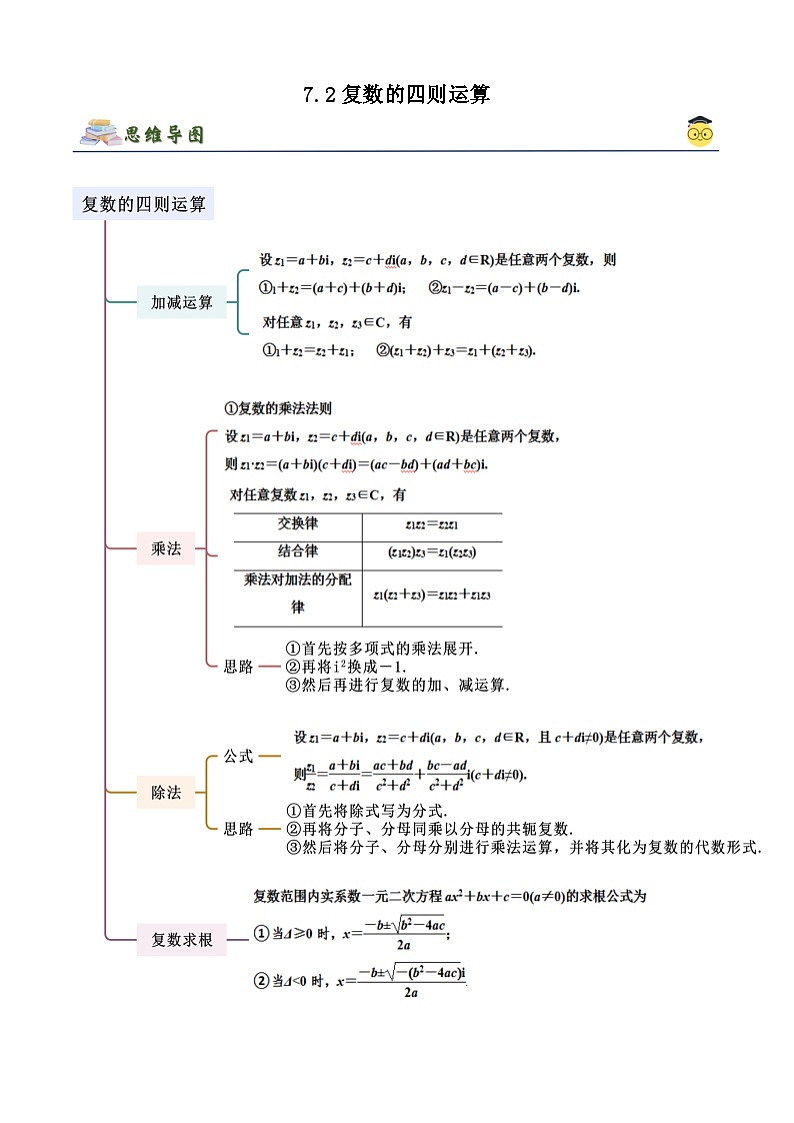
高中数学人教A版 (2019)必修 第二册7.2 复数的四则运算精品同步训练题

这是一份高中数学人教A版 (2019)必修 第二册7.2 复数的四则运算精品同步训练题，文件包含人教版高中数学必修二精讲精练72复数的四则运算原卷版docx、人教版高中数学必修二精讲精练72复数的四则运算解析版docx等2份试卷配套教学资源，其中试卷共36页， 欢迎下载使用。

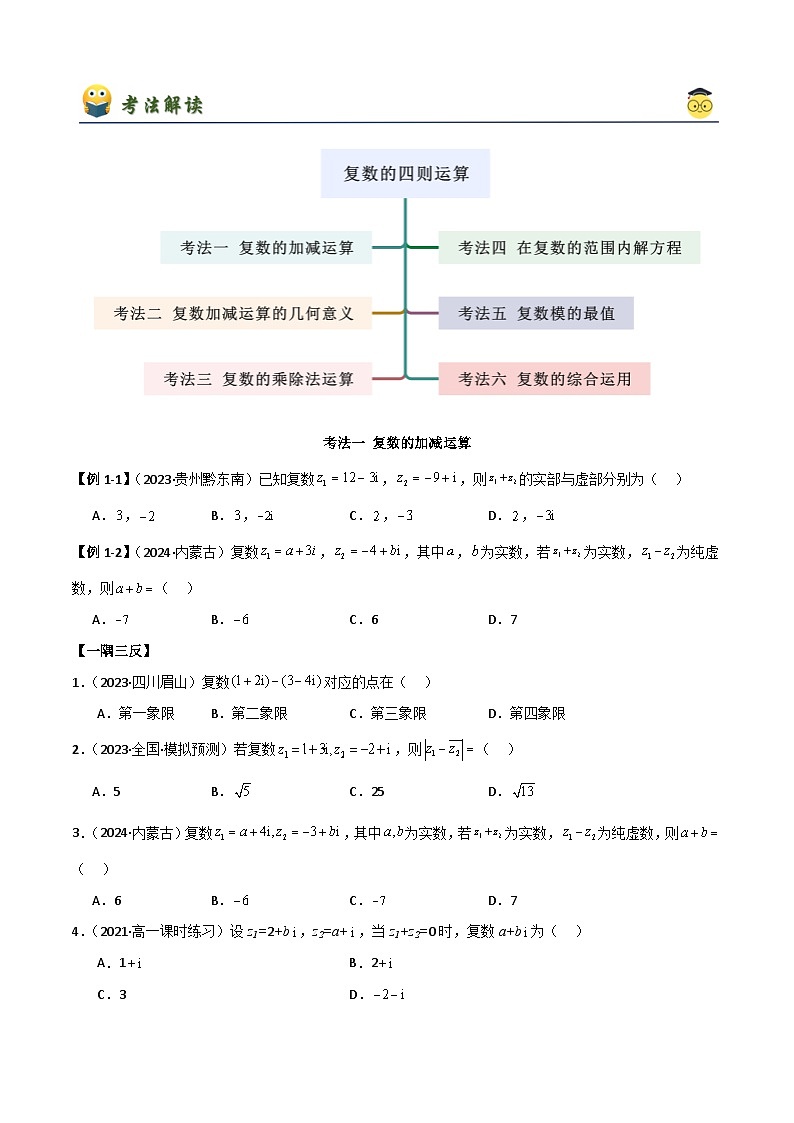
考法一 复数的加减运算
【例1-1】（2023·贵州黔东南）已知复数，，则的实部与虚部分别为（ ）
A．，B．，C．，D．，
【答案】A
【解析】因为，，所以，其实部与虚部分别为，.故选：A
【例1-2】（2024·内蒙古）复数，，其中，为实数，若为实数，为纯虚数，则（ ）
A．B．C．6D．7
【答案】A
【解析】由题意，，
因为为实数，为纯虚数，所以，得，
所以.故选：A.
【一隅三反】
1．（2023·四川眉山）复数对应的点在（ ）
A．第一象限B．第二象限C．第三象限D．第四象限
【答案】B
【解析】由复数，可得复数在复平面内对应的点位于第二象限.故选：B.
2．（2023·全国·模拟预测）若复数，则（ ）
A．5B．C．25D．
【答案】A
【解析】由，有，则，所以，故选：A．
3．（2024·内蒙古）复数，其中为实数，若为实数，为纯虚数，则（ ）
A．6B．C．D．7
【答案】C
【解析】复数，为实数，则，
由为实数，得，解得，又，
显然，由为纯虚数，得，解得，
所以.故选：C
4．（2021·高一课时练习）设z1=2+b，z2=a+，当z1+z2=0时，复数a+b为（ ）
A．1+B．2+
C．3D．
【答案】D
【解析】因为z1+z2=(2+b)+(a+)=(2+a)+(b+1)=0，所以于是
故.故选：D.
考法二 复数加减运算的几何意义
【例2-1】（2023上海）若向量分别表示复数，则=（ ）
A．B．C．D．
【答案】B
【解析】因为，又向量分别表示复数，
所以表示复数，所以.故选：B
【例2-2】（2023·江苏常州）已知，，，则（ ）
A．B．C．D．
【答案】B
【解析】在复平面中，设分别与向量对应，
由题意可得，，
因为，
即，解得，即.
故选：B.
【一隅三反】
1．（2023·河南郑州）复数与分别表示向量与，则表示向量的复数为（ ）
A．B．C．D．
【答案】D
【解析】复数与分别表示向量与，
因为，所以表示向量的复数为.
故选：D.
2．（2023·高一课时练习）复平面上有A、B、C三点，点对应的复数为，对应的复数为，对应的复数为，则点的坐标为 ．
【答案】
【解析】因为对应的复数是，对应的复数为，又，
所以对应的复数为，又，
所以点对应的复数为，所以点的坐标为．故答案为：．
3．（2023·高一课时练习）在平行四边形ABCD中，若点A，C分别对应于复数，，则A，C两点间的距离为 ．
【答案】5
【解析】依题意得对应的复数为，
所以A，C两点间的距离为．
故答案为：5．
考法三 复数的乘除法运算
【例3】（2023·全国·高一随堂练习）计算：
(1)；(2)；(3)；(4)；(5)；(6)．
【答案】(1)(2)(3)1(4)(5)(6)
【解析】（1）
（2）
（3）
（4）
（5）
（6）
【一隅三反】
1.（2023·全国·高一随堂练习）计算：
(1)；(2)；(3)；(4)．
【答案】(1)(2)(3)(4)
【解析】（1）
（2）
（3）
（4）
2．（2023·全国·高一随堂练习）计算：
(1)；(2)；(3)；(4)．
【答案】(1)(2)(3)(4)
【解析】（1）
（2）
（3）
（4）
；
3.（2023湖北）计算：（1）；
（2）．
（3）；
（4）．
【答案】（1）513；（2）．（3）；（4）.
【解析】（1）由于
故
（2）由于，，，
故
（3），，所以，，
因此，原式；
（4）因为，
所以原式．
考法四 在复数的范围内解方程
【例4】（2024云南）在复数范围内解下列方程.
(1)；(2)；(3).
【答案】(1)(2)(3)
【解析】（1）∵，∴由求根公式得.
（2）∵，∴由求根公式得.
（3）∵，∴由求根公式得.
【一隅三反】
1．（2023下·西藏林芝·高一校考期末）在复数范围内解下列方程：
(1)；(2)．(3)；(4)．
【答案】(1)(2)(3)或．(4)或．
【解析】（1）即为，故.
（2）即为，
故，所以.
（3），则，则.
（4）配方，得．或，所以或．
2（2024上海）已知是关于x的方程的一个根，求实数p、q的值及方程的另一个根．
【答案】，，另一个根．
【解析】因为是方程的一个根，
所以，
即，
所以，解得，
所以方程为，
因为，
所以方程的另一个根是.
3（2024江苏）已知复数，i为虚数单位.
（1）求和；
（2）若复数z是关于x的方程的一个根，求实数m，n的值.
【解析】（1）复数
，
，．
（2）复数是关于的方程的一个根，
，
，，
，
解得，．
考法五 复数模的最值
【例5】（2023·浙江）已知复数z满足，则的取值范围为 ．
【答案】
【解析】表示对应的点是单位圆上的点，
的几何意义表示单位圆上的点和之间的距离，
的取值范围转化为点到圆心的距离加上半径可得最大值，
减去半径可得最小值，
所以最大距离为，最小距离为，
所以的取值范围为.
故答案为：.

【一隅三反】
1．（2024·上海）已知，且，为虚数单位，则的最大值是 ．
【答案】8
【解析】因为且，
所以，根据复数模的几何意义，表示以为圆心，3为半径的圆，
所以，表示圆上的点和点的距离，
因为圆心到点的距离为，
，
故答案为：
2．（2023·全国·模拟预测）设是复数且，则的最小值为（ ）
A．1B．C．D．
【答案】C
【解析】根据复数模的几何意义可知，表示复平面内以为圆心，1为半径的圆，而表示复数到原点的距离，
由图可知，.故选：C
3．（2024北京）（多选）已知i为虚数单位，下列说法正确的是（ ）
A．若复数z满足，则复数z在复平面内对应的点在以为圆心，为半径的圆上
B．若复数z满足，则复数
C．复数的模实质上是复平面内复数对应的点到原点的距离，也就是复数对应的向量的模
D．非零复数z1对应的向量为，非零复数z2对应的向量为，若，则
【答案】CD
【解析】对于A项，设，则，
由可得，，
所以满足的复数z在复平面内对应的点在以为圆心，为半径的圆上，故A错误；
对于B项，设，则，
由可得，，
根据复数相等的条件可得，解得，
所以，故B项错误；
对于C项，由复数的模的定义知C正确；
对于D项，由的几何意义知，以为邻边的平行四边形为矩形，从而两邻边垂直，故D正确.故选：CD.
考法六 复数的综合运用
【例6】（2024·浙江宁波）（多选）已知复数，，则下列结论正确的有（ ）
A．B．C．D．
【答案】BC
【解析】设，，其中.
对于选项A: ，所以与不一定相等，故选项A错误；
对于选项B: 因为，
所以，
因为，
所以,故选项B正确；
对于选项C: 因为,
所有
因为，
所以,故选项C正确；
对于选项D:因为，所以
，而与不一定相等,故选项D错误；
故选：BC.
【一隅三反】
1．（2024·云南德宏）（多选）已知是复数的共轭复数，则下列说法正确的是（ ）
A．B．若，则
C．D．若，则的最小值为1
【答案】CD
【解析】对于A，设，则，但，故A错误；
对于B，令，满足，故B错误；
对于C，设，则所以，则，所以，故C正确；
对于D，设，则，
即，表示以为圆心，半径为1的圆，
表示圆上的点到的距离，故的最小值为，故D正确.
故选：CD
2（2023湖北 ）（多选）设，是复数，则（ ）
A．B．若，则
C．若，则D．若，则
【答案】AC
【解析】设，，a，b，x，，
，A成立；
，则，所以，，
从而，所以，C成立；
对于B，取，，满足，但结论不成立；
对于D，取，，满足，但结论不成立.
故选：AC
3．（2024甘肃（多选））设是复数，则下列命题中的真命题是（ ）
A．若，则
B．若，则
C．若，则
D．若，则
【答案】ABC
【解析】对于A，因，则，即，则为真，A正确；
对于B，因，则和互为共轭复数，则为真，B正确；
对于C，设，因，则，即，
于是得，则为真，C正确；
对于D，当，有，而，即为假，D不正确.
故选：ABC
单选题
1．（2024·湖南邵阳）下列各式的运算结果不是纯虚数的是（ ）
A．B．
C．D．
【答案】D
【解析】对于A，，故A正确；
对于B，，故B正确；
对于C，，故C正确；
对于D，，故D错误.
故选：D.
2．（2024·云南昆明）复数在复平面内对应的点位于（ ）
A．第一象限B．第二象限C．第三象限D．第四象限
【答案】A
【解析】由题意，所以复数在复平面内对应的点为，它在第一象限.
故选：A.
3．（2024上·山东枣庄）若是方程的一个虚数根，则（ ）
A．0B．-1C．D．-1或
【答案】A
【解析】方程化为：，依题意，或，
显然，又，即，
所以.
故选：A
4．（2023·安徽）若复数满足，则的虚部为 （ ）
A．B．C．D．
【答案】D
【解析】由，得，
所以，即的虚部为故选：D．
5．（2024·湖北武汉）已知复数满足，则（ ）
A．3B．C．7D．13
【答案】B
【解析】由题设，
令，且，则
所以，故，故.
故选：B
6．（2023·广东中山）复数满足，其中为虚数单位，则（ ）
A．B．
C．D．
【答案】A
【解析】由，得，，
对于A，，A正确；
对于B，，B错误；
对于C，，C错误；
对于D，，D错误.
故选：A
7．（2024·河北保定）已知复数满足，则在复平面内对应的点位于（ ）
A．第一象限B．第二象限
C．第三象限D．第四象限
【答案】A
【解析】由，得，
所以，所以，
所以在复平面内对应的点为，位于第一象限.
故选：A.
8．（2023·全国·统考模拟预测）已知复数，且，则的最小值为（ ）
A．B．C．D．
【答案】C
【解析】因为，
，
，
，
，
所以，当时，，故的最小值为.
故选：C.
多选题
9（2023福建 ）若实数，满足，则（ ）
A．的共轭复数为B．
C．的值可能为D．
【答案】BCD
【解析】因为.
所以，，
即，，则.解得或，
故A错误，B，C，D均正确.
故选：BCD.
10．（2024河北邢台 ）若复数z满足（其中是虚数单位），则（ ）
A．z的实部是2B．z的虚部是
C．D．
【答案】CD
【解析】依题意，两边乘以得，
所以的实部为，虚部为，所以AB错误.
，所以C正确.
，所以D正确.
故选：CD
11．（2024·河南南阳）设复数的共轭复数为，则下列结论正确的有（ ）
A．B．
C．D．
【答案】AC
【解析】对于A，，故A正确；
对于B，，故B错误；
对于C，，所以，故C正确；
对于D，，，所以，故D错误.
故选：AC
12．（2023·湖南衡阳）在复平面内，复数，正确的是（ ）
A．复数的模长为1
B．复数在复平面内对应的点在第二象限
C．复数是方程的解
D．复数满足
【答案】AC
【解析】由得，则
对于A,，故A正确，
对于B, 复数在复平面内对应的点为，故该点位于第四象限，故B错误，
对于C, ,故是的复数根，故C正确，
对于D，设复数对应的向量为到,复数对应的向量为,由得的距离为1，故复数对应点的在以为圆心，半径为1的圆上，故的最大值为，故D错误，
故选：AC
填空题
13．（2023·上海黄浦）复数，在复平面上对应的点分别为，，则 ；
【答案】
【解析】因为复数，在复平面上对应的点分别为，，则，
则故答案为：
14．（2023·上海宝山）已知复数，满足，，，则在复平面所对应的点组成的图形的面积为 ．
【答案】
【解析】，是以复平面内点为圆心，以为半径的圆，
， ，
，即，
复数以复平面内点为圆心，半径为1和的两圆构成的圆弧，
则在复平面所对应的点组成的图形的面积为：
故答案为：.
15．（2024·课时练习）若有两个数，它们的和是4，积为5，则这两个数是 .
【答案】
【解析】设，依题意有，
即，所以.将代入，得；将代入，解得；将代入，得，结合解得或.所以对应的数为、.
故答案为：
16．（2023上海）已知为虚数单位，则集合中元素的个数为___________.
【答案】
【解析】当时，；
当时，；
当时，；
当时，，所以集合中元素的个数为．
故答案为：．
解答题
17．（2023·浙江·）已知复数z满足（i是虚数单位）
(1)求z的值；
(2)若复数在复平面内对应的点在第三象限，求实数m的取值范围.
【答案】(1)；
(2).
【解析】（1）由，得.
（2）由（1）知，
，由复数在复平面内对应的点在第三象限，
得，解得，
所以实数m的取值范围为.
18．（2023·浙江）已知复数，其中是正实数，是虚数单位．
(1)如果为纯虚数，求实数的值；
(2)如果，是关于的方程的一个复根，求的值．
【答案】(1)；
(2).
【解析】（1）解：因为，
由为纯虚数，可得，解得；
（2）解：因为，
所以，，
将代入方程，
得，
即有，
所以，
.
19．（2023·广东东莞）已知和均为实数，其中是虚数单位.
(1)求复数z；
(2)若对应的点在第四象限，求实数m的取值范围.
【答案】(1)
(2)
【解析】（1），
，
，
由题意，，可得，则
（2），
由题意，，解得或.
实数的取值范围是.
20．（2023·辽宁沈阳）在①复数z满足和均为实数；②为复数z的共轭复数，且；③复数是关于x方程的一个根，这三个条件中任选一个（如果选择多个条件分别解答，按第一个解答计分），并解答问题：
(1)求复数z；
(2)在复平面内，若对应的点在第四象限，求实数m的取值范围.
【答案】(1)
(2)
【解析】（1）若选①：设，
则，，
若和均为实数，则，解得，
所以；
若选②：设，则，
因为，则，
整理得，
则，解得，
所以；
若选③：因为，则，解得，
且，所以.
（2）由（1）可得，
则，
若对应的点在第四象限，则，解得或，
所以实数m的取值范围为.
21．（2023上·广东深圳）已知复数，，其中i为虚数单位，且满足，且为纯虚数.
(1)若复数，在复平面内对应点在第一象限，求复数z；
(2)求；
(3)若在（1）中条件下的复数z是关于x的方程的一个根，求实数m，n的值.
【答案】(1)
(2)答案见解析
(3)，
【解析】（1）因为复数，，所以，
又为纯虚数，所以，
又，所以，
又因为复数z在复平面内对应点在第一象限，
所以，故.
（2）由（1）可知
当时，，
当时，.
（3）法一：由（1）可知是关于x的方程的一个根，
所以把，代入得，
化简得，
即，解得：，
法二：由（1）可知是关于x的方程的一个根，
所以此方程的另一根为：，则，
解得：，
22．（2024·全国·高三专题练习）已知关于的二次方程．
(1)当为何值时，这个方程有一个实根？
(2)是否存在，使得原方程有纯虚数根？若存在，求出的值；若不存在，试说明理由．
【答案】(1)
(2)不存在，理由见解析
【解析】（1）设是方程的一个实根，则
即
根据复数相等的意义知
解得：．
所以，当时，原方程有一实根．
（2）假定方程有纯虚数根（，且），代入原方程得
即
由复数相等意义知
但方程即无实数解，即实数不存在．
所以，对任何实数，原方程不可能有纯虚数根．