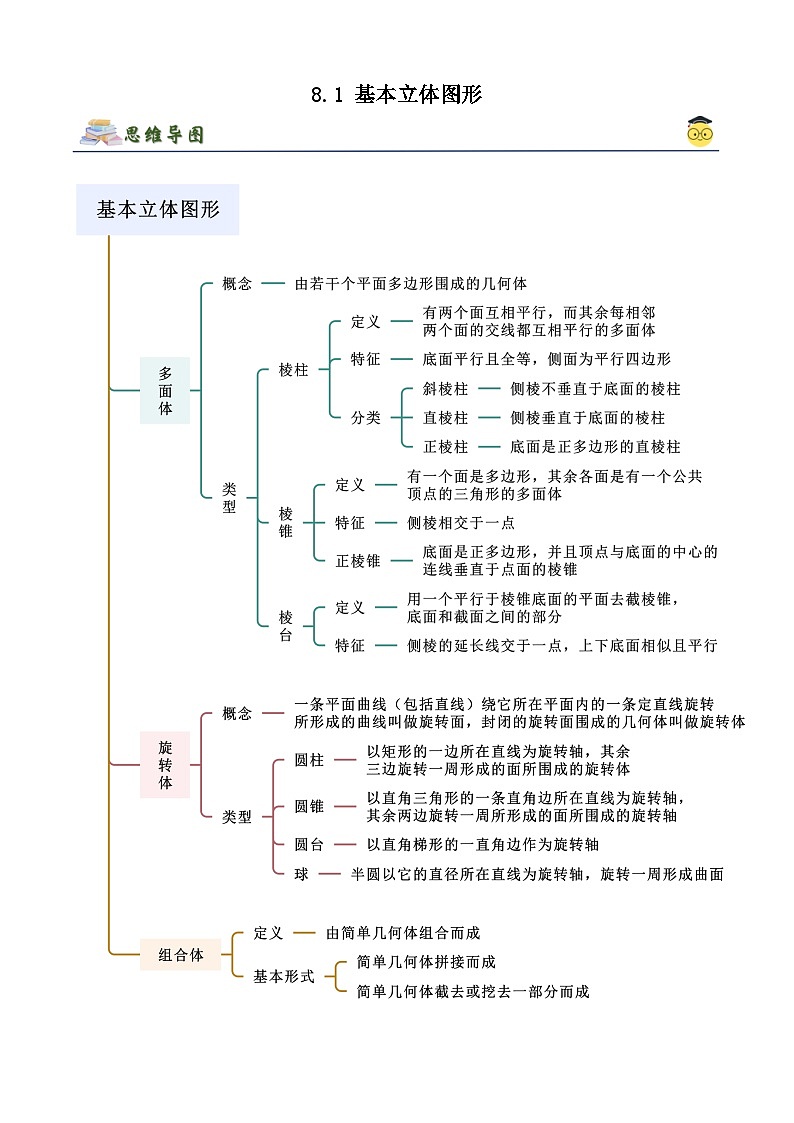
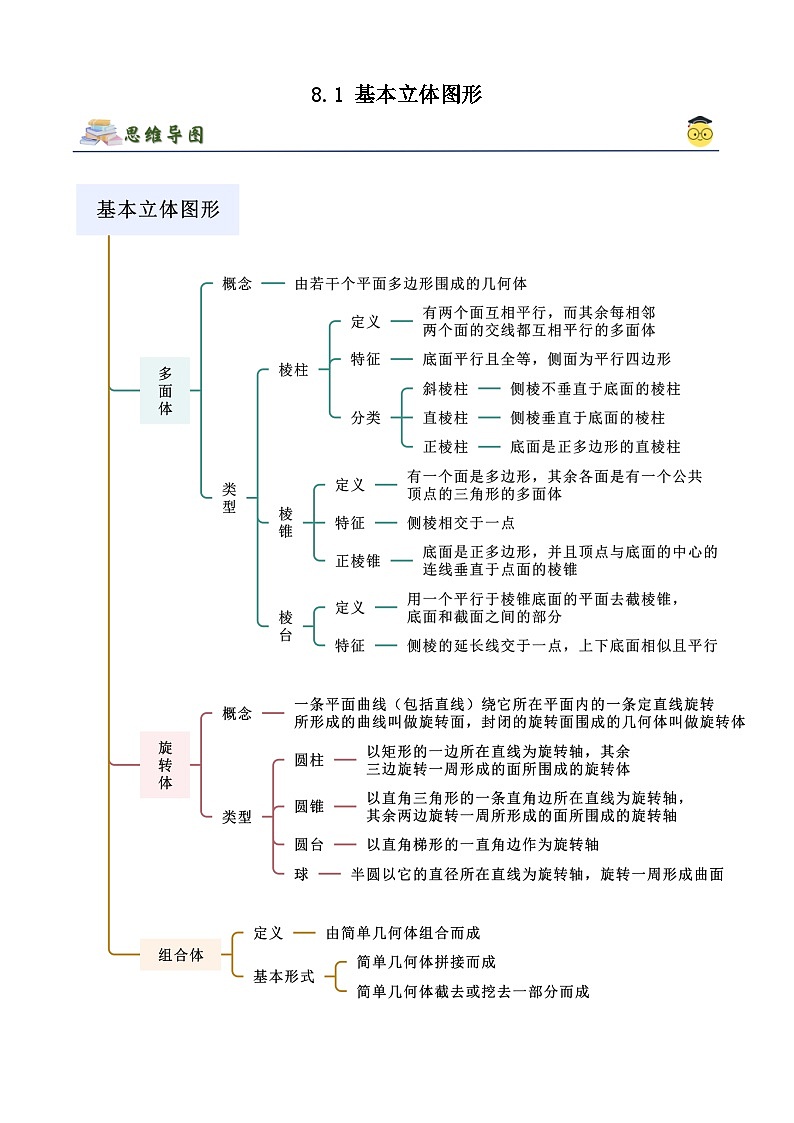
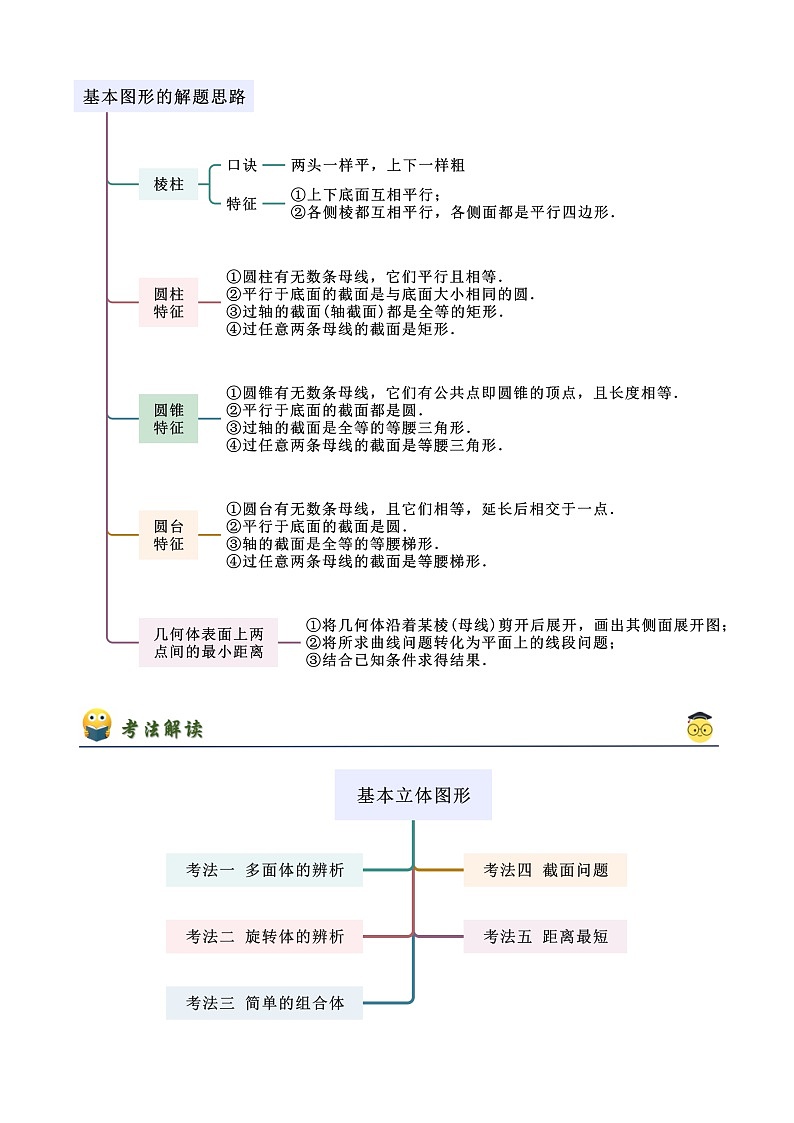
高中数学人教A版 (2019)必修 第二册8.1 基本立体图形优秀课堂检测
展开考法一 多面体的辨析
【例1-1】(2023·四川内江)观察下面的几何体,哪些是棱柱?( )
A.(1)(3)(5)B.(1)(2)(3)(5)
C.(1)(3)(5)(6)D.(3)(4)(6)(7)
【答案】A
【解析】根据棱柱的结构特征:一对平行的平面且侧棱相互平行的几何体,所以,棱柱有(1)(3)(5).
故选:A
【例1-2】(2023广西崇左)下列几何体中是棱锥的有( )
A.0个B.1个C.2个D.3个
【答案】C
【解析】由棱锥的定义可得,只有几何体⑤、⑥为棱锥.故选:C.
【例1-3】(2024·山西晋城)下面四个几何体中,是棱台的是( )
A.B.C.D.
【答案】B
【解析】A是圆台,D是棱锥,C侧棱延长没有交于一点,故不是四棱台,B是三棱台.故选:B
【例1-4】(2024·江苏)下列说法中,正确的个数为( )
(1)有两个面互相平行,其余四个面都是等腰梯形的六面体是棱台
(2)由若干个平面多边形所围成的几何体是多面体
(3)棱锥的侧棱长与底面多边形的边长相等,则此棱锥可能是正六棱锥
(4)底面是等边三角形,侧面都是等腰三角形的三棱锥是正三棱锥
A.3个B.2个C.1个D.0
【答案】C
【解析】(1)
如图,侧棱延长线可能不交于一点,故(1)错误
(2)正确,符合多面体的定义
(3)不正确,不存在这样的正六棱锥,正六边形中心与各个顶点连线,构成了6个全等的小正三角,所以正六棱锥棱长不可能与底边相等,故(3)错误.
(4)错误 . 不一定是正三棱锥,如图所示:
三棱锥中有. 满足底面为等边三角形. 三个侧面 ,, 都是等腰三角形,但长度不一定等于,即三条侧棱不一定全部相等.
故选:C
【一隅三反】
1.(2023下·重庆万州·高一校考阶段练习)下列图形中,不是棱柱的是( )
A. B. C. D.
【答案】D
【解析】一般地,有两个面互相平行,其余各面都是四边形,
并且相邻两个四边形的公共边互相平行,由这些面所围成的多面体叫做棱柱.
故A为四棱柱,B为三棱柱,C为四棱柱,
D中有两个面为梯形,两个面为三角形且三角形面不平行,故D不是棱柱.
故选:D
2.(2024云南)下面图形中,为棱锥的是( )
A.①③B.③④C.①②④D.①②
【答案】C
【解析】根据棱锥的定义和结构特征可以判断,①②是棱锥,③不是棱锥,④是棱锥.故选:C
3.(2024湖北)下面四个几何体中,是棱台的是( )
A.B.C.D.
【答案】C
【解析】A项中的几何体是棱柱.
B项中的几何体是棱锥;
D项中的几何体的棱AA′,BB′,CC′,DD′没有交于一点,则D项中的几何体不是棱台;
C项中的几何体是由一个棱锥被一个平行于底面的平面截去一个棱锥剩余的部分,符合棱台的定义,是棱台.
故选:C
4.(2023上·广东惠州)下列说法不正确的是( )
A.直四棱柱是长方体B.正方体是平行六面体
C.长方体是平行六面体D.平行六面体是四棱柱
【答案】A
【解析】对于选项A,直四棱柱的侧棱垂直底面,当底面不是矩形时直四棱柱不是长方体,
故A错误;
对于选项B,正方体的对面平行,是平行六面体,故B正确;
对于选项C,长方体的对面平行,是平行六面体,故C正确;
对于选项D,平行六面体是底面为平行四边形的四棱柱,故D正确;
故选:A.
5.(2023江西)下列说法正确的是______(填序号).
①有两个面互相平行,其余各面都是四边形的几何体是棱柱;
②有两个面互相平行,其余各面都是平行四边形的几何体是棱柱;
③有一个面是多边形,其余各面都是三角形的几何体是棱锥;
④用一个平面去截棱锥,棱锥底面和截面之间那部分的几何体是棱台;
⑤存在一个四棱锥,其四个侧面都是直角三角形.
【答案】⑤
【解析】对于①,有两个面互相平行,其余各面都是四边形,并且相邻两个四边形的公共边都互相平行,由这些面所围成的多面体叫做棱柱,故①不正确;
对于②,如图1中的几何体,满足有两个面互相平行,其余各面都是平行四边形,但其不是棱柱,故②不正确;
对于③,有一个面是多边形,其余各面都是有一个公共顶点的三角形,由这些面所围成的多面体叫做棱锥,故③不正确;
对于④,由棱台的定义,知截面和棱锥的底面平行,故④不正确;
对于⑤,如图2所示,在正方体中,四棱的四个侧面均为直角三角形,故⑤正确.
图1 图2
故答案为:⑤.
考法二 旋转体的辨析
【例2-1】(2024·宁夏)如图所示,观察下面四个几何体,其中判断正确的是( )
A.①是圆台B.②是圆台C.③是圆锥D.④是圆台
【答案】C
【解析】图①不是由圆锥截得的,所以①不是圆台;
图②上下两个面不平行,所以②不是圆台;
图④不是由圆锥截得的,所以④不是圆台;很明显③是圆锥,
故选:C.
【例2-2】(2023湖北)下列命题中错误的是( )
A.圆柱的母线与轴平行
B.圆锥的轴截面是所有过顶点的截面中面积最大的一个
C.圆锥的所有轴截面是全等的等腰三角形
D.圆柱的所有平行于底面的截面都是圆面
【答案】B
【解析】A:圆柱的母线即为圆柱的高线,与轴平行,即A正确;
B:因为轴截面的顶角为时,截面面积为,当时,为最大的;当时,不是最大的,因为存在不过定点的截面等于,,B错误;
C:圆锥所有截面的顶角相等且两腰长均为母线,C正确;
D:根据圆柱的性质可判断D正确.
故选:B
【例2-3】(2023湖南)下列关于球体的说法中,错误的是( ).
A.球面是空间中到定点的距离等于定长的点的集合
B.用一个平面去截一个球得到的截面是圆面
C.一个圆绕其直径所在直线旋转一周形成的曲面所围成的几何体是球体
D.球的对称轴只有1条
【答案】D
【解析】对于A,球面是空间中到定点的距离等于定长的点的集合是正确的;
对于B,用一个平面去截一个球得到的截面是圆面是正确;
对于C,一个圆绕其直径所在直线旋转一周形成的曲面所围成的几何体是球体是正确的;
对于D,球的每一条直径都是对称轴,有无数条,故D错误.
故选:D
【一隅三反】
1.(2023河北)如图所示的图形中有
A.圆柱、圆锥和圆台B.圆柱和圆锥
C.圆柱和圆台D.棱柱、棱锥和圆锥
【答案】B
【解析】根据题中图形可知,(1)是圆柱;(2)是圆锥;(3)不是圆台,因为上下两个面不平行;
因此图所示的图形中有圆柱和圆锥,故选:B.
2(2023·广东佛山)(多选)下列关于圆柱的说法中正确的是( )
A.圆柱的所有母线长都相等
B.用平行于圆柱底面的平面截圆柱,截面是与底面全等的圆面
C.用一个不平行于圆柱底面的平面截圆柱,截面是一个圆面
D.一个矩形以其对边中点的连线为旋转轴,旋转所形成的几何体是圆柱
【答案】ABD
【解析】对于A,圆柱的所有母线长都等于圆柱的高,且都相等,所以A正确,
对于B,用平行于圆柱底面的平面截圆柱,由圆柱的性质可知截面是与底面全等的圆面,所以B正确,
对于C,用一个不平行于圆柱底面的平面截圆柱,截面是椭圆面或椭圆面的一部分,所以C错误,
对于D,一个矩形以其对边中点的连线为旋转轴,旋转所形成的几何体是圆柱,所以D正确,
故选:ABD
3(2023上海)给出下列命题:
①在圆柱的上、下底面的圆周上各取一点,则这两点的连线是圆柱的母线;
②圆锥的顶点与底面圆周上任意一点的连线是圆锥的母线;
③在圆台的上、下底面的圆周上各取一点,则这两点的连线是圆台的母线;
④圆柱的任意两条母线所在的直线是互相平行的;
⑤圆台所有母线的延长线交于一点其中正确的命题是( )
A.①②④B.②③④C.①③⑤D.②④⑤
【答案】D
【解析】由于圆柱母线所在的直线互相平行且与旋转轴平行,而在圆柱的上、下底面的圆周上各取一点,
这两点的连线与旋转轴不一定平行,故①错误,④正确;由圆锥母线的定义知②正确;
在圆台的上、下底面的圆周上各取一点,这两点的连线不一定是母线,
且圆台所有母线的延长线交于一点,故③错误,⑤正确.故选:D.
4.(2024广东深圳)(多选)下列关于球体的说法正确的是( )
A.球体是空间中到定点的距离等于定长的点的集合
B.球面是空间中到定点的距离等于定长的点的集合
C.一个圆绕其直径所在直线旋转一周形成的曲面所围成的几何体是球体
D.球的对称轴只有1条
【答案】BC
【解析】空间中到定点的距离等于定长的点的集合是球面,所以A错误,B正确;
由球体的定义,知C正确;球的每一条直径所在的直线均为它的对称轴,所以D错误.故选:BC.
考法三 简单的组合体
【例3-1】(2023·广东深圳)如图所示的几何体是数学奥林匹克能赛的奖杯,该几何体由( )
A.一个球、一个四棱柱、一个圆台构成
B.一个球、一个长方体、一个棱台构成
C.一个球、一个四棱台、一个圆台构成
D.一个球、一个五棱柱、一个校台构成
【答案】B
【解析】由图可知,该几何体是由一个球、一个长方体、一个棱台构成.故选:B.
【例3-2】(2024江苏)将一个等腰梯形绕着它的较长的底边所在直线旋转一周,所得的几何体包括( )
A.一个圆台、两个圆锥B.一个圆台、一个圆柱
C.两个圆台、一个圆柱D.一个圆柱、两个圆锥
【答案】D
【解析】设等腰梯形,较长的底边为,
则绕着底边旋转一周可得一个圆柱和两个圆锥,
轴截面如图,
故选:D
【一隅三反】
1.(2024安徽合肥)如图所示的简单组合体的组成是( )
A.棱柱、棱台B.棱柱、棱锥
C.棱锥、棱台D.棱柱、棱柱
【答案】B
【解析】由图知,简单组合体是由棱锥、棱柱组合而成.故选:B.
2.(2023·江苏无锡)如图,长方体被一个平面截成两个几何体,其中,这两个几何体分别是( )
A.三棱柱和四棱柱 B.三棱柱和五棱柱C.三棱台和五棱台D.三棱柱和六棱柱
【答案】B
【解析】由于,所以,所以几何体为三棱柱,几何体为五棱柱,故选:B
3(2023上海)将一个等腰梯形绕着它的较长的底边所在的直线旋转一周,所得的几何体是由 ( )
A.一个圆台、两个圆锥构成B.两个圆台、一个圆锥构成
C.两个圆柱、一个圆锥构成D.一个圆柱、两个圆锥构成
【答案】D
【解析】旋转体如图,中间是一个圆柱,两端是相同的圆锥构成,故选D.
考法四 截面问题
【例4-1】(2023·浙江衢州)用一个平面去截一个正方体,所得截面形状可能为:( )
①三角形②四边形③五边形④六边形⑤圆
A.①②③B.①②④C.①②③④D.①②③④⑤
【答案】C
【解析】用一个平面去截一个正方体,分别是所在棱的中点,所得截面形状可能为三角形、四边形、五边形、六边形,
如图所示:
故选:C.
【例4-2】.(2023·河南新乡)如图,在棱长为2的正方体中,是棱的中点,过三点的截面把正方体分成两部分,则该截面的周长为( )
A.B.C.D.
【答案】A
【解析】如图,取BC的中点,连接EF,AF,,
、分别为棱、的中点,则,正方体中,则有,所以平面为所求截面,因为正方体的棱长为2,所以,,,所以四边形的周长为.故选:A.
【一隅三反】
1.(2024甘肃)如图所示的几何体是由一个圆柱挖去一个以圆柱的上底面为底面,下底面圆心为顶点的圆锥而得到的组合体,现用一个垂直于圆柱底面的平面去截这个组合体﹐则截面图形可能是 (填序号).
【答案】①⑤
【解析】由题意,当截面过旋转轴时,圆锥的轴截面为等腰三角形,此时①符合条件;
当截面不过旋转轴时,圆锥的轴截面为双曲线的一支,此时⑤符合条件,
综上可知截面的图形可能是①⑤.
故答案为:①⑤
2.(2023下·江苏盐城)如图,在正方体中,的中点为Q,过A,Q,三点的截面是( )
A.三角形B.矩形C.菱形D.梯形
【答案】D
【解析】如图所示,取的中点P,连接PQ、、、和,
,分别是,的中点,故,且,
,故,,故四点共面,
故四边形是过A,Q,三点的截面,且四边形是梯形.
故选:D.
3.(2023上·上海普陀·高二校考期中)如图,在棱长为的正方体中,点分别是棱的中点,则由点确定的平面截正方体所得的截面多边形的周长等于 .
【答案】6
【解析】作(实际上)交于,延长交延长线于.连接交于点,可证分别是的中点,同理取中点,连接,六边形即为截面,该六边形为正六边形,由正方体棱长为易得正六边形边长为1,周长为6.
故答案为:6.
4.(2023·四川成都)如图,正方体的棱长为4,E是侧棱的中点,则平面截正方体所得的截面图形的周长是 .
【答案】
【解析】取中点,连接,,
∵中点为,E是侧棱的中点,
∴,,
又在直角三角形中,
∴,
∵正方体中,
∴四边形为平行四边形,
∴
∴,
四点共面,即为正方体的截面.
在直角三角形中,
同理,则截面周长为.故答案为:.
考法五 距离最短
【例5-1】(2023·上海浦东新)如图,在长方体中,,点为上的动点,则的最小值为( )
A.5B.C.D.
【答案】D
【解析】将绕翻折到与共面,平面图形如下所示:
连接,则的长度即为的最小值,
因为,所以 ,
所以,所以,即的最小值为.
故选:D
【例5-2】(2023下·河北张家口·高一统考期末)在三棱锥中,,,一只蜗牛从点出发,绕三棱锥三个侧面爬行一周后,到棱的中点,则蜗牛爬行的最短距离是().
A.B.C.D.
【答案】D
【解析】如图所示,将三棱锥的侧面展开,则线段为所求,
由题意得,,
由余弦定理可得,
则,即蜗牛爬行的最短距离是.
故选:D.
【例5-3】(2023·全国·模拟预测)如图,在棱长为1的正方体中,点P在侧面上运动,则的最小值为 .
【答案】
【解析】在正方体的右侧补一个同样大小的正方体,得到如图所示的长方体,
由对称性可知,故.
故答案为:
【一隅三反】
1.(2024河北)如图,底面半径为1,高为2的圆柱,在点A处有一只蚂蚁,现在这只蚂蚁要围绕圆柱由点A爬到点B,则蚂蚁爬行的最短路线的长是__________.
【答案】
【解析】把圆柱的侧面沿剪开,然后展开成平面图形:矩形,在矩形中求最短距离即可.如图所示,连接,则即为蚂蚁爬行的最短距离.∵,且,
∴
∴蚂蚁爬行的最短路线的长为.
故答案为:
(2023·四川南充)在直三棱柱中分别为的中点,沿棱柱的表面从到两点的最短路径的长度为
【答案】
【解析】由题意得直三棱柱底面为等腰直角三角形.
①若把面和面展开在同一个平面内,则线段在直角三角形中,
由勾股定理得;
②若把面和面展开在同一个平面内,则线段在直角三角形中,
此时.
③若把面和面展开在同一个平面内,设的中点为,
在直角三角形中,由勾股定理得.
④若把面和面展开在同一个面内,
过作与行的直线,过作与平行的直线,
所作两直线交于点,则在直角三角形中,
由勾股定理得.
由于,
可得从到两点的最短路径的长度为,
故选:B
3.(2023上·江西南昌)如图,在长方体中,若,且面对角线上存在一点使得最短,则的最小值为 .
【答案】
【解析】把沿翻折,使矩形和在一个平面上,连接,
则的最小值为,
在中,可知,
由余弦定理得,
所以的最小值为.
故答案为:.
4.(2023上·重庆南岸)如图,在长方体中,且,为棱上的一点.当取得最小值时,的长为 .
【答案】
【解析】将侧面、侧面延展至同一平面,如下图所示:
当点、、三点共线时,取最小值,
在上图矩形中,,,则,即,
此时,点为的中点,
如下图所示,连接,
易知四边形是边长为的正方形,则,
因为平面,平面,所以,,
又因为为的中点,所以,,
由勾股定理可得.
故答案为:.
5.(2024·山西)如图,直四棱柱侧棱长为4cm,底面是长为5cm 宽为3cm的长方形.一只蚂蚁从顶点A出发沿棱柱的表面爬到顶点B.求:
(1)蚂蚁经过的最短路程;
(2)蚂蚁沿着棱爬行(不能重复爬行同一条棱)的最长路程.
【答案】(1);(2).
【解析】(1)将长方体与顶点相关的两个面展开,共有三种方式,如图所示:
则的长就为最短路线.
若蚂蚁沿前侧面和上底面爬行,如图1,
则经过的最短路程为,
若蚂蚁沿侧面爬行,如图2,
则经过的最短路程为,
若蚂蚁沿左侧面和上底面爬行,如图3,
则经过的最短路程为,
,
∴所以蚂蚁经过的最短路程是;
单选题
1.(2023·陕西西安)下列说法正确的是( )
A.有两个平面互相平行,其余各面都是平行四边形的多面体是棱柱
B.三棱锥的三个侧面都可以是直角三角形
C.有两个面互相平行,其余各面都是梯形的多面体是棱台
D.以三角形的一条边所在直线为旋转轴,其余两边旋转形成的曲面所围成的几何体叫圆锥
【答案】B
【解析】对于A,如图(1)符合条件但却不是棱柱;
对于B,在图(2)所示的正方体中,
三棱锥的三个侧面都是直角三角形,故B正确.
对于C,如图(3),其侧棱不相交于一点,故不是棱台.
对于D,如图(4),以直角三角形的斜边为轴旋转得到的是两个对底的圆锥.
故选:B.
2.(2024·湖北宜昌)设有四个命题,其中真命题的个数是( )
①有两个平面互相平行,其余各面都是四边形的多面体一定是棱柱;②以直角三角形的一边为轴旋转一周所得到的旋转体是圆锥;③用一个面去截棱锥,底面与截面之间的部分叫棱台;④侧面都是长方形的棱柱叫长方体.
A.0个B.1个C.2个D.3个
【答案】A
【解析】对①,棱台也满足上下底面平行,且其余各面都是四边形.故①错误.
对②,若以直角三角形的斜边为轴旋转一周则得到的旋转体不是圆锥.故②错误.
对③,面去截棱锥需要面与底面平行才能得出棱台,故③错误.
对④,正三棱柱满足侧面都是长方形,但不是长方体,故④错误.
故选:A
3.(2024·云南)用长为8,宽为4的矩形做侧面围成一个圆柱,则圆柱的轴截面的面积为( ).
A.32B.C.D.
【答案】B
【解析】当圆柱的高时,,
所以圆柱的轴截面的面积为;
当圆柱的高,,
所以圆柱的轴截面的面积为,
故选:B
4.(2023下·安徽合肥·高一合肥市第七中学校考阶段练习)下列命题中成立的是( )
A.有两个相邻侧面是矩形的棱柱是直棱柱
B.各个面都是三角形的多面体一定是棱锥
C.一个棱锥的侧面是全等的等腰三角形,那它一定是正棱锥
D.各个侧面都是矩形的棱柱是长方体
【答案】A
【解析】对A,以三棱柱为例,如图,若侧面和侧面为矩形,则.
又平面ABC,所以 面,
又棱柱侧棱互相平行,故其他侧棱也与底面垂直.
所以此三棱柱为直三棱柱,故A正确;
对B,如图所示的八面体满足每个面都是三角形,但它不是棱锥,故B不正确;
对C,如图所示的三棱锥中有,满足侧面是全等的等腰三角形,
但它不是正三棱锥,故C不正确;
对D,各个侧面都是矩形且上下底面也是矩形的棱柱才是长方体,故D不正确.
故选:A
5.(2023·四川内江·高二四川省资中县第二中学校考阶段练习)如图,已知圆柱体底面圆的半径为,高为,、分别是两底面的直径,、是母线.若一只小虫从点出发,从侧面爬行到点,求小虫爬行的最短路径为( )
A.B.C.D.
【答案】B
【解析】展开圆柱的侧面如图所示,
展开后,在矩形中,,,
由图可知小虫爬行路线的最短长度是.
故选:B.
6.(2023·贵州六盘水)下面的四个长方体中,是由上边的平面图形围成的是( )
A.B.
C.D.
【答案】D
【解析】由长方体的展开图可得符合的长方体为D.故选:D.
7.(2024北京)对如图中的组合体的结构特征有以下几种说法,其中说法正确的是( )
A.由一个长方体割去一个四棱柱所构成的
B.由一个长方体与1个四棱柱组合而成的
C.由一个长方体挖去一个四棱台所构成的
D.由一个长方体与两个四棱台组合而成的
【答案】A
【解析】如图,该组合体可由一个长方体割去一个四棱柱所构成,也可以由一个长方体与两个四棱柱组合而成,如下图所示:
故选:A
8.(2023上·湖北)一个透明密闭的正方体容器中恰好盛有该容器一半容积的水,任意转动这个正方体容器,则水面在容器中形成的所有可能的形状是( )
①三角形 ②非正方形的菱形 ③五边形 ④正方形 ⑤正六边形
A.②④B.③④⑤C.②④⑤D.①②③④⑤
【答案】C
【解析】因为正方体容器中盛有一半容积的水,无论怎样转动,其水面总是过正方体的中心,
过正方体一面上一边的中点和此边外的顶点以及正方体的中心作一截面,其截面形状为菱形,且不为正方形,所以②是正确的;
过正方体一面上相对两边的中点以及正方体的中心作一截面,得截面形状为正方形,所以④是正确的;
过正方体的一个面相邻两边的中点以及正方体的中心作一截面,得截面形状为正六边形,所以⑤是正确的;
过正方体的中心的平面截正方体得到的截面,且该截面将正方体的体积平分,显然截面不能是三角形和五边形;
故选:C.
多选题
9.(2024·湖北)下面关于空间几何体叙述正确的是( )
A.正四棱柱是长方体
B.底面是正多边形的棱锥是正棱锥
C.有两个面互相平行,其余各面都是梯形的多面体是棱台
D.直角三角形以其直角边所在直线为轴旋转,其余两边旋转一周形成的面所围成的旋转体是圆锥
【答案】AD
【解析】于A选项,正四棱柱是长方体,A选项正确;
对于B选项,底面是正多边形,但侧棱长不相等的棱锥不是正棱锥,B选项错误;
对于C选项,有两个面互相平行,其余各面都是梯形,但侧棱的延长不交于一点的几何体不是棱台,C选项错误;
对于D选项,直角三角形以其直角边所在直线为轴旋转,其余两边旋转一周形成的面所围成的旋转体是圆锥,D选项正确.
故选:AD.
10.(2024安徽)下列说法正确的是( )
A.如果四棱锥的底面是正方形,那么这个四棱锥的四条侧棱都相等
B.五棱锥只有五条棱
C.一个棱柱至少有五个面
D.棱台的各侧棱延长后交于一点
【答案】CD
【解析】四棱锥的底面是正方形,它的侧棱可以相等,也可以不相等,A错误;
五棱锥除了五条侧棱外,底面上还有五条棱,故共条棱,B错误;
一个棱柱最少有三个侧面,两个底面,故至少有五个面,C正确;
棱台是由平行于棱锥底面的截面截得,故棱台的各侧棱延长后交于一点,D正确.故选:CD.
11.(2023·重庆沙坪坝)下列关于空间几何体的说法正确的是( )
A.棱柱的两个底面是全等的多边形,且对应边互相平行
B.棱柱的侧棱都相等,侧面都是平行四边形
C.各个面都是三角形的几何体是三棱锥
D.圆柱的任意两条母线互相平行
【答案】ABD
【解析】对于A,由棱柱的结构特征知:棱柱两个底面为全等的多边形,且对应边互相平行,A正确;
对于B,由棱柱的结构特征知:棱柱侧棱长相等,且各侧面均为平行四边形,B正确;
对于C,如下图所示的两个三棱锥拼接而成的组合体,各个面都为三角形,但不是三棱锥,C错误;
对于D,由圆柱的结构特征知:圆柱的任意两条母线互相平行,D正确.
故选:ABD.
12.(2023下·江苏南京 )在正方体中,点是线段上的动点,若过三点的平面将正方体截为两个部分,则所得截面的形状可能为( )
A.等边三角形B.矩形
C.菱形D.等腰梯形
【答案】ABD
【解析】当点与重合时,过三点的截面是等边三角形,A正确;
当点与重合时,过三点的截面为矩形,B正确;
若截面为菱形,则必有,此时点与重合,故C错误;
当点与中点重合时,记的中点为F,连接,
易知,由正方体性质可知,且,所以四边形为平行四边形,
所以,所以且,设正方体棱长为2,则,
所以过三点的截面为等腰梯形,D正确.
故选:ABD
填空题
13.(2023山西)圆柱的母线长为5,底面半径为2,称过圆柱的轴的任意平面与圆柱形成的平面为轴截面,则该圆柱轴截面面积为 .
【答案】20
【解析】轴截面为矩形,两边长分别为5和4,故轴截面的面积为.故答案为:20
14.(2023·上海)如图,一圆柱体的底面周长为,高为,是上底面的直径.一只昆虫从点出发,沿着圆柱的侧面爬行到点,昆虫爬行的最短路程是 .
【答案】
【解析】作出圆柱的侧面展开图如下图所示,
则当昆虫的爬行路线为线段时,爬行的路程最短,
圆柱体的底面周长为,;
最短路程为:.
故答案为:.
15.(2023·上海浦东新)已知圆锥的轴截面是一个顶角为,腰长为2的等腰三角形,则经过该圆锥任意两条母线的平面截圆锥所得截面面积最大值是 .
【答案】2
【解析】由题意可知圆锥的母线为
设圆锥任意两条母线的夹角为,则经过该圆锥任意两条母线的平面截圆锥所得截面面积为,由于,故当时,面积最大为2,故答案为:2
16.(2023·上海长宁)正多面体各个面都是全等的正多边形,其中,面数最少的是正四面体,面数最多的是正二十面体,它们被称为柏拉图多面体.如图,正二十面体是由个等边三角形所组成的正多面体.已知多面体满足:顶点数-棱数+面数=,则正二十面体的顶点的个数为 .
【答案】
【解析】由于正二十面体是由个等边三角形所组成的正多面体,所以面数为,并且每个顶点处有条棱,设正二十面体共有个顶点,则棱数为,由题意可得,解得.则正二十面体的顶点的个数为故答案为:.
解答题
17.(2023·上海)如图所示,圆柱侧面上有两点、,在处有一只蜘蛛,在处有一只苍蝇,蜘蛛沿怎样的路线行走才能以最短的路程抓住苍蝇?最短路程是多少?
【答案】详见解析.
【解析】如图,将圆柱的侧面沿母线展开即得矩形,
其中,分别为,的中点,
在矩形中,,,
连接,则;
可知蜘蛛沿着爬行时路程最短,最短路程为.
18.(2023上·上海·高二专题练习)已知是直角梯形与底边垂直的一腰(如图).分别以,,,为轴旋转,试说明所得几何体是由哪些简单几何体构成的?
【答案】答案见解析
【解析】①以AB边为轴旋转所得旋转体是圆台;如图(1)所示;
②以BC边为轴旋转所得旋转体是一组合体:下部为圆柱,上部为圆锥;如图(2)所示;
③以CD边为轴旋转所得旋转体为一组合体:上部为圆锥,下部为圆台,再挖去一个小圆锥;
如图(3)所示.
④以AD边为轴旋转得到一个组合体,它是一个圆柱上部挖去一个圆锥;如图(4)所示.
19.(2023·安徽滁州)已知长方体中,,,,E,F分别为,的中点,求过D,E,F三点截得长方体的截面的周长.
【答案】
【解析】延长EF分别交,的延长线于点M,N,连接MD,ND,分别交,于点Q,P,
连接PF,EQ,则过D,E,F三点截得长方体的平面为五边形.
过F点作,过点作,所以是的中点,是的中点.
在中,,,所以.
在中,,所以,,
则,,.
同理在中,,在中,,,
所以,,所以截面周长为.
20.(2022·高二课时练习)如图,把四个半径都是1的球中的三个放在桌面上,使它们两两外切,然后在它们上面放上第四个球,使它与前三个都相切,在这四个球之间有一个小球和这四个球都外切,求这个小球的半径.
【答案】.
【解析】由题意可知:连接四个球的球心,得到一个棱长为2的正四面体,设正四面体为PABC,
设四面体PABC的外接球球心为O,半径为R,
设PO的延长线与底面ABC的交点为D,则PD为正四面体PABC的高,PD⊥底面ABC,且PO=R,
棱长为2,所以AD=,
所以,
在中,,
,即:
解得:R=.
与4个球都相切的小球的球心也在O处,所以小球的半径
21.(2023上·上海浦东新)对于精美的礼物,通常人们会用包装纸把礼物包好,还会用彩带捆扎包装好的礼物,有时还会扎出一个花结.这些包装彩带也不便宜,因此在捆扎时不仅要考虑美观、结实,也要考虑尽量地节省包装彩带.以长方体的礼物为例,较为典型的两种捆扎方式分别为“十字”和“对角”,如下图所示.
假设1:将礼物视作一个长方体,其长为4,宽为2、高为1;假设2:不考虑花结处的彩带,将每一段彩带视为线段,且完全位于礼物的表面上;假设3:“十字”捆扎中,长方体表面上的每一段彩带(上底面和下底面各2段,每个侧面各1段)都与其相交的棱垂直;假设4:“对角”捆扎中,以某种方式展开长方体后,长方体表面上的每一段彩带(上底面和下底面各2段,每个侧面各1段)在其表面展开图上均落在同一条直线上.
(1)求“十字”捆扎中彩带的总长度;
(2)根据假设4绘制示意图,求“对角”捆扎中彩带的总长度,并比较两种捆扎方式,给出用彩带捆扎礼物的建议.
【答案】(1)
(2),在实际生活中包装彩带时应选择“对角”捆扎的方式,更节省包装彩带
【解析】(1)采用“十字”捆扎中彩带的总长度为;
(2)
由于,因此在实际生活中包装彩带时应选择“对角”捆扎的方式,更节省包装彩带.
22.(2023·浙江温州)近些年来,三维扫描技术得到空前发展,从而催生了数字几何这一新兴学科.数字几何是传统几何和计算机科学相结合的产物.数字几何中的一个重要概念是曲率,用曲率来刻画几何体的弯曲程度.规定:多面体在顶点处的曲率等于与多面体在该点的所有面角之和的差(多面体的面角是指多面体的面上的多边形的内角的大小,用弧度制表示),多面体在面上非顶点处的曲率均为零.由此可知,多面体的总曲率等于该多面体各顶点的曲率之和.例如:正方体在每个顶点有个面角,每个面角是,所以正方体在各顶点的曲率为 ,故其总曲率为.
(1)求四棱锥的总曲率;
(2)表面经过连续变形可以变为球面的多面体称为简单多面体.关于简单多面体有著名欧拉定理:设简单多面体的顶点数为,棱数为,面数为,则有:.利用此定理试证明:简单多面体的总曲率是常数.
【答案】(1)
(2)证明见解析
【解析】(1)四棱锥有个顶点,个三角形面,个凸四边形面,故其总曲率为
(2)设多面体有个面,给组成多面体的多边形编号,分别为号.
设第 号 多边形有 条边.
则多面体共有条棱.
由题意,多面体共有个顶点.
号多边形的内角之和为,故所有多边形的内角之和为
故多面体的总曲率为
所以满足题目要求的多面体的总曲率为.
“十字”捆扎
“对角”捆扎
人教A版 (2019)必修 第二册第九章 统计9.1 随机抽样精品当堂检测题: 这是一份人教A版 (2019)必修 第二册<a href="/sx/tb_c4000309_t7/?tag_id=28" target="_blank">第九章 统计9.1 随机抽样精品当堂检测题</a>,文件包含人教版高中数学必修二精讲精练91随机抽样原卷版docx、人教版高中数学必修二精讲精练91随机抽样解析版docx等2份试卷配套教学资源,其中试卷共31页, 欢迎下载使用。
人教A版 (2019)8.2 立体图形的直观图精品测试题: 这是一份人教A版 (2019)<a href="/sx/tb_c4000302_t7/?tag_id=28" target="_blank">8.2 立体图形的直观图精品测试题</a>,文件包含人教版高中数学必修二精讲精练82立体图形的直观图原卷版docx、人教版高中数学必修二精讲精练82立体图形的直观图解析版docx等2份试卷配套教学资源,其中试卷共45页, 欢迎下载使用。
必修 第二册第六章 平面向量及其应用6.3 平面向量基本定理及坐标表示精品综合训练题: 这是一份必修 第二册<a href="/sx/tb_c4000292_t7/?tag_id=28" target="_blank">第六章 平面向量及其应用6.3 平面向量基本定理及坐标表示精品综合训练题</a>,文件包含人教版高中数学必修二精讲精练63平面向量基本定理及坐标表示原卷版docx、人教版高中数学必修二精讲精练63平面向量基本定理及坐标表示解析版docx等2份试卷配套教学资源,其中试卷共50页, 欢迎下载使用。













