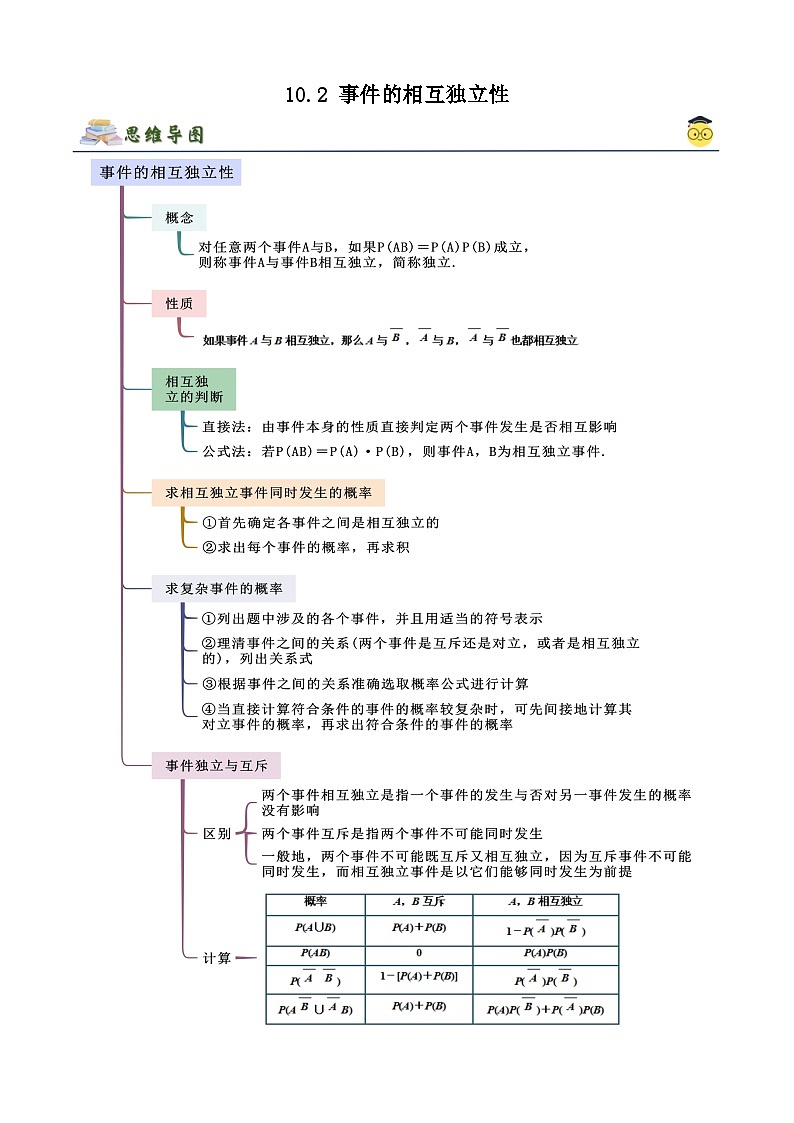
高中数学人教A版 (2019)必修 第二册10.2 事件的相互独立性精品课后作业题

这是一份高中数学人教A版 (2019)必修 第二册10.2 事件的相互独立性精品课后作业题，文件包含人教版高中数学必修二精讲精练102事件的相互独立性原卷版docx、人教版高中数学必修二精讲精练102事件的相互独立性解析版docx等2份试卷配套教学资源，其中试卷共42页， 欢迎下载使用。


考法一 独立事件的判断
【例1-1】（2023陕西）篮球比赛中，张英皓同学投球三次，设事件A为“三次投球全不是三分球”，事件B为“三次全是三分球”，事件C为“三次投球不全是三分球”，则下列结论正确的是（ ）
A．A与C对立B．B与C对立C．任两个均对立D．任两个均不对立
【答案】B
【解析】篮球比赛中，张英皓同学投球三次，设事件为“三次投球全不是三分球”，
事件为“三次全是三分球”，事件为“三次投球不全是三分球”，
对于，事件与事件能同时发生，不是对立事件，故错误；
对于，事件与事件是对立事件，故正确；
对于，事件与事件能同时发生，不是对立事件，故错误；
对于，事件与事件是对立事件，故错误．
故选：．
【例1-2】（2023北京）连续抛掷一枚质地均匀的硬币2次，设“第1次正面朝上”为事件，“第2次反面朝上”为事件，“2次朝上结果相同”为事件，有下列三个命题：
①事件与事件相互独立；②事件与事件相互独立；③事件与事件相互独立．
以上命题中，正确的个数是（ ）
A．0B．1C．2D．3
【答案】D
【解析】抛掷两枚质地均匀的硬币的所有结果是：(正，正)，(正，反)，(反，正)，(反，反)，
由题意得，，，
．
因为，故事件相互独立，①正确；
因为，故事件相互独立，②正确；
因为，故事件相互独立，③正确．
故选：D
【一隅三反】
1．（2023·山东）（多选）下列事件A，B不是独立事件的是（ ）
A．一枚硬币掷两次，A=“第一次为正面向上”，B=“第二次为反面向上”
B．袋中有两个白球和两个黑球，不放回地摸两球，A=“第一次摸到白球”，B=“第二次摸到白球”
C．掷一枚骰子，A=“出现点数为奇数”，B=“出现点数为偶数”
D．A=“人能活到20岁”，B=“人能活到50岁”
【答案】BCD
【解析】对于A选项，两个事件发生，没有关系，故是相互独立事件；
对于B选项，A事件发生时，影响到B事件，故不是相互独立事件；
对于C选项，由于投的是一个骰子，是对立事件，所以不是相互独立事件；
对于D选项，能活到20岁的，可能也能活到50岁，故不是相互独立事件.
故选：BCD.
2．（2023江西吉安）（多选）某人连续掷两次骰子，表示事件“第一次掷出的点数是2”，表示事件“第二次掷出的点数是3”．表示事件“两次掷出的点数之和为5”，表示事件“两次掷出的点数之和为9”．则（ ）
A．与相互独立B．与相互独立
C．与不相互独立D．与不相互独立
【答案】ACD
【解析】由题意知，，
，
．
对A：∵，∴与相互独立，故A正确．
对B：∵，∴与不相互独立，故B错误．
对C：∵，∴与不相互独立，故C正确．
对D：∵，∴与不相互独立，故D正确．
故选：ACD.
3．（2024辽宁大连）（多选）有6个相同的球，分别标有数字1，2，3，4，5，6，从中有放回的随机取两次，每次取1个球，甲表示事件“第一次取出的球的数字是1”，乙表示事件“第二次取出的球的数字是2”，丙表示事件“两次取出的球的数字之和是8”，丁表示事件“两次取出的球的数字之和是7”，则（ ）
A．甲与丙相互独立B．甲与丁相互独立
C．乙与丙不相互独立D．丙与丁不相互独立
【答案】BCD
【解析】两次取出的球的数字之和为8，有共5种情况，
所以；两次取出的球的数字之和为7，有共6种情况，
所以；；
对于A，，故甲与丙不相互独立，错误；
对于B，，故甲与丁相互独立，正确；
对于C，，故乙与丙不相互独立，正确；
对于D，，故丙与丁不相互独立，正确.
故选：BCD
考法二 独立事件的乘法公式
【例2-1】（2023江西·开学考试）2023年10月26日神舟十七号载人飞船成功发射，某校举办航天知识竞赛，竞赛设置了，，三道必答题目.已知某同学能正确回答，，题目的概率分别为0.8，0.7，0.5，且回答各题是否正确相互独立，则该同学最多有两道题目回答正确的概率为（ ）
A．0.56B．0.72C．0.89D．0.92
【答案】B
【解析】，，三道必答题目，该同学都回答正确的概率为，
该同学最多有两道题目回答正确的概率为.
故选：B.
【例2-2】（2023河南）甲、乙两个篮球队进行比赛，获胜队将代表所在区参加市级比赛，他们约定，先赢四场比赛的队伍获胜．假设每场甲、乙两队获胜的概率均为，每场比赛不存在平局且比赛结果相互独立，若在前三场比赛中，甲队赢了两场，乙队赢了一场，则最终甲队获胜的概率为 ．
【答案】/
【解析】由题意得甲、乙两队获胜的概率均为，且最多再进行四场比赛，最少再进行两场比赛.
则①再进行两场比赛甲队获胜的概率为；
②再进行三场比赛甲队获胜的概率为；
③再进行四场比赛甲队获胜的概率为，
由互斥事件的概率加法公式，可得最终甲队获胜的概率为．
故答案为.
【一隅三反】
1．（2023河南驻马店）如图，用三个不同的元件连接成一个系统．当元件正常工作且元件至少有一个正常工作时，系统正常工作．已知元件正常工作的概率依次为，则系统能正常工作的概率为 ．
【答案】/
【解析】系统能正常工作，则至少有个能正常工作且能正常公式，
所以系统能正常工作的概率为.
故答案为：
2．（2023全国·课时练习）如图，已知电路中有4个开关，每个开关独立工作，且闭合的概率为，则灯亮的概率为 ．

【答案】/0.8125
【解析】记开关闭合为事件A，B，C，D，
因为开关断开且开关至少有一个断开时，线路才断开，导致灯不亮，
所以灯不亮的概率为,
所以灯亮的概率为.
故答案为：
3．（2023安徽亳州·期末）“秋风起．月渐圆，桂树落叶，兔儿下凡间”．中秋节是中国传统节日，为了让更多的小朋友参与到中秋节的欢乐氛围中来，秦皇岛市青少年宫特别推出了“团圆中秋喜迎国庆”——中秋猜灯谜活动，欢迎小朋友们前来，感受传统文化的熏陶，品味传统习俗的趣味．现有甲，乙两位小朋友组成“快乐宝贝队”参加猜灯谜活动，每轮活动由甲，乙各猜一个灯谜，已知甲每轮猜对的概率为，乙每轮精对的概率为．在每轮活动中，甲和乙猜对与否互不影响，各轮结果也互不影响，则“快乐宝贝队”在两轮活动中猜对2个灯谜的概率为 ．
【答案】
【解析】设分别表示甲两轮猜对个，个，个灯谜的事件，分别表示乙两轮猜对个，个，个灯谜的事件．根据独立事件的性质，可得
，
，
设“两轮活动‘快乐宝贝队’猜对2个灯谜”，则，且互斥，与，与，与分别相互独立，所以
，因此，“快乐宝贝队”在两轮活动中猜对2个灯谜的概率是．
故答案为：
4．（2024黑龙江 ）2023年10月26日神舟十七号载人飞船发射任务取得圆满成功，开启了我国空间站应用发展的新阶段.太空站内甲，乙､丙三名航天员分别出仓进行同一试验，已知甲､乙､丙试验成功的概率分别为，若三人能否试验成功相互独立，且三人中恰有2人试验成功的概率为，则三人中只有甲､乙两人试验成功的概率的最大值为 .
【答案】
【解析】因为三人能否试验成功相互独立，且三人中恰有2人试验成功的概率为，
所以，所以.
所以（当且仅当时取“”），即.
解得或，即或，
又因为，所以，
所以，当且仅当时取等号.
三人中只有甲､乙两人试验成功的概率为.
故答案为：
考法三 独立事件与互斥事件
【例3-1】（2023江苏宿迁·期末）下列关于互斥事件、对立事件、独立事件（上述事件的概率都大于零）的说法中正确的是（ ）
A．互斥事件一定是对立事件B．对立事件一定是互斥事件
C．互斥事件一定是独立事件D．独立事件一定是互斥事件
【答案】B
【解析】互斥事件不一定是对立事件，对立事件一定是互斥事件，故A错误，B正确；
互斥事件一定不能同时发生，而独立事件可以同时发生，所以互斥事件一定不是独立事件，独立事件可能互斥也可能不互斥，故C，D均错误.
故选：B.
【例3-2】（2023陕西咸阳）（多选）国家于2021年8月20日表决通过了关于修改人口与计划生育法的决定，修改后的人口计生法规定，国家提倡适龄婚育、优生优育，一对夫妻可以生育三个子女，该政策被称为三孩政策．某个家庭积极响应该政策，一共生育了三个小孩．假定生男孩和生女孩是等可能的，记事件：该家庭既有男孩又有女孩；事件：该家庭最多有一个男孩；事件：该家庭最多有一个女孩．通过判断或计算可知，下列说法正确的是（ ）
A．事件与事件互斥且对立B．事件与事件互斥且对立
C．事件与事件相互独立D．事件与事件相互独立
【答案】AD
【解析】有三个小孩的家庭的样本空间：
={(男,男,男),(男,男,女),(男,女,男),(女,男,男),(男,女,女),(女,男,女),(女,女,男),(女,女,女)}，
事件={(男,男,女),(男,女,男),(女,男,男),(男,女,女),(女,男,女),(女,女,男)}
事件={(男,女,女),(女,男,女),(女,女,男),(女,女,女)}，
事件={(男,男,男),(男,男,女),(男,女,男),(女,男,男)}，
对于A，,且，则事件B与事件C互斥且对立，A正确；
对于B，{(男,女,女),(女,男,女),(女,女,男)}，则事件与事件不互斥，B错误；
对于C，事件有4个样本点，事件有4个样本点，事件有0个样本点，
，显然，即事件与事件不相互独立，C错误；
对于D，事件有6个样本点，事件有4个样本点，事件有3个样本点，
，显然，即事件与事件相互独立，D正确.
故选：AD
【一隅三反】
1．（2023河南焦作）（多选）一个不透明袋子中装有大小和质地完全相同的2个红球和3个白球，从袋中一次性随机摸出2个球，则（ ）
A．“摸到2个红球”与“摸到2个白球”是互斥事件
B．“至少摸到1个红球”与“摸到2个白球”是对立事件
C．“摸出的球颜色相同”的概率为
D．“摸出的球中有红球”与“摸出的球中有白球”相互独立
【答案】ABC
【解析】2个红球为，3个白球为，则任意摸出2个球有，共10种，
“摸到2个红球”有，“摸到2个白球”有，“至少摸到1个红球”有，
“摸出的球颜色相同”有，“摸出的球中有白球” 有，“摸出的球颜色不相同”有，
A：“摸到2个红球”与“摸到2个白球”不可能同时发生，故是互斥事件，故A正确；
B：“至少摸到1个红球”与“摸到2个白球”不可能同时发生，且必有一个发生，故是对立事件，故B正确；
C：给每个球编号，不同的摸球结果有10种，“摸出的球颜色相同”包含4种结果，故其概率为，故C正确；
D：设“摸出的球中有红球”，“摸出的球中有白球”，用古典概型的方法计算可知
，，，显然，故，不相互独立，故D错误.
故选：ABC
2（2023北京）分别掷两枚质地均匀的硬币，“第一枚为正面”记为事件A，“第二枚为正面”记为事件B，“两枚结果相同”记为事件C，那么事件A与B，A与C间的关系是（ ）
A．A与B，A与C均相互独立
B．A与B相互独立，A与C互斥
C．A与B，A与C均互斥
D．A与B互斥，A与C相互独立
【答案】A
【解析】因为事件A是否发生对事件B、C是否发生不产生影响，所以A与B，A与C均相互独立.
故选：A
3．（2024湖南岳阳）（多选）将一枚质地均匀且标有数字1，2，3，4，5，6的骰子随机掷两次，记录每次正面朝上的数字，甲表示事件“第一次掷出的数字是1”，乙表示事件“第二次掷出的数字是2”，丙表示事件“两次掷出的数字之和是8”，丁表示事件“两次掷出的数字之和是7”.则（ ）
A．事件甲与事件丙是互斥事件
B．事件甲与事件丁是相互独立事件
C．事件乙包含于事件丙
D．事件丙与事件丁是对立事件
【答案】AB
【解析】由题意，事件甲：第一次掷出的数字是1有：，
事件乙：第二次掷出的数字是2有：，
事件丙：两点数之和为8的所有可能为：，
事件丁：两点数之和为7的所有可能为：，
其中，
对于A中，事件甲与事件丙不能同时发生，所以事件甲与事件丙是互斥事件，所以A正确；
对于B中，由，所以，
所以事件甲与事件丁是相互独立事件，所以B正确；
对于C中，事件乙不包含于事件丙，所以C错误；
对于D中，根据对立事件的定义，可得事件丙与事件丁不对立，所以D错误.
故选：AB.
4．（2023高一·全国·随堂练习）已知事件A，B发生的概率分别为，，分别在A，B互斥和独立的条件下，求出下列事件的概率并填入表中：
【答案】答案见解析
考法四 独立事件的实际应用
【例4】（2023高一上·安徽）与国家安全有关的问题越来越受到社会的关注和重视.为了普及国家安全教育，某校组织了一次国家安全知识竞赛，已知甲、乙、丙三位同学答对某道题目的概率分别为，，，且三人答题互不影响.
(1)求甲、乙两位同学恰有一个人答对的概率；
(2)若甲、乙、丙三个人中至少有一个人答对的概率为，求的值.
【答案】(1)
(2)
【解析】（1）设“甲答对”，“乙答对”，
则，，，，
“甲，乙两位同学恰有一个人答对”的事件为，且与互斥
由三人答题互不影响，知A，互相独立，则A与，与，与均相互独立，
则，
所以甲，乙两位同学恰有一个人答对的概率为.
（2）设“丙答对”，则，
设“甲，乙，丙三个人中至少有一个人答对”，由（1）知，
，解得，
所以的值为.
【一隅三反】
1．（2023湖南长沙·期末）某校举行围棋比赛，甲､乙､丙三人通过初赛，进入决赛.决赛比赛规则如下：首先通过抽签的形式确定甲､乙两人进行第一局比赛，丙轮空；第一局比赛结束后，胜利者和丙进行比赛，失败者轮空，以此类推，每局比赛的胜利者跟本局比赛轮空者进行下一局比赛，直到一人累计获胜三局，则此人获得比赛胜利，比赛结束.假设每局比赛双方获胜的概率均为，且每局比赛相互独立.
(1)求丙每局都获胜的概率
(2)求甲获得比赛胜利的概率.
【答案】(1)
(2)
【解析】（1）丙每局都获胜有以下两种情况：第一局甲获胜，后三局丙获胜；第一局乙获胜，后三局丙获胜，
第一局甲获胜，后三局丙获胜的概率，
第一局乙获胜，后三局丙获胜的概率，
丙每局都获胜的概率.
（2）设甲获胜为事件，乙获胜为事件，丙获胜为事件，
比赛进行三局，甲获胜的概率为，
比赛进行五局，有以下6种情况：AABBA，AABCA，ACBAA，ACCAA，BBAAA，BCAAA，
甲获胜的概率为，
比赛进行七局，有一下8种情况：
AABCCBA，ACBBCAA，ACBACBA，ACCABBA，BBACCAA，BCAACBA，BCABCAA，.
甲获胜的概率为，
故甲获得比赛胜利的概率为.
2．（2024湖南）为迎接第二届湖南旅发大会，郴州某校举办“走遍五大洲，最美有郴州”知识能力测评，共有1000名学生参加，随机抽取了100名学生，记录他们的分数，将数据分成4组：，并整理得到如下频率分布直方图：

(1)根据直方图，估计这次知识能力测评的平均数；
(2)用分层随机抽样的方法从，两个区间共抽取出4名学生，再从这4名学生中随机抽取2名依次进行交流分享，求第二个交流分享的学生成绩在区间的概率；
(3)学校决定从知识能力测评中抽出成绩最好的两个同学甲乙进行现场知识抢答赛，比赛共设三个项目，每个项目胜方得1分，负方得0分，没有平局．三个项目比赛结束后，总得分高的人获得冠军．已知甲在三个项目中获胜的概率分别为，各项目的比赛结果相互独立，甲至少得1分的概率是，甲乙两人谁获得最终胜利的可能性大？并说明理由．
【答案】(1)分
(2)
(3)甲最终获胜的可能性大；理由见解析
【解析】（1）解：由频率分布直方图，根据平均数的计算公式，估计这次知识能力测评的平均数：
分.
（2）解：由频率分布直方图，可得的频率为，的频率为，
所以用分层随机抽样的方法从，两个区间共抽取出4名学生，
可得从抽取人，即为，从中抽取人，即为，
从这4名学生中随机抽取2名依次进行交流分享，有 ，共有12个基本事件；
其中第二个交流分享的学生成绩在区间的有：，共有3个，
所以概率为.
（3）解：甲最终获胜的可能性大.
理由如下：由题意，甲至少得1分的概率是，
可得，其中，解得，
则甲的2分或3分的概率为：，
所以乙得分为2分或3分的概率为，
因为，所以甲最终获胜的可能性更大.
单选题
1．（2023广东顺德 ）某工厂有甲、乙、丙三名工人进行零件安装比赛，甲每个零件的安装完成时间少于丙的概率为.乙每个零件的安装完成时间少于丙的概率为，比赛要求甲、乙、丙各安装一个零件，且他们安装每个零件相互独立，则甲和乙中至少有一人安装完成时间少于丙的概率为（ ）
A．B．C．D．
【答案】C
【解析】甲和乙安装完成时间均多于丙的概率为，
甲和乙中至少有一人安装完成时间少于丙的概率为.
故选：C.
2．（2024江西萍乡）甲、乙两选手进行象棋比赛，已知每局比赛甲获胜的概率为0.6，乙获胜的概率为0.4，若采用三局二胜制，则乙最终获胜的概率为（ ）
A．0.36B．0.352C．0.288D．0.648
【答案】B
【解析】由题意可得乙最终获胜有两种情况：
一是前两局乙获胜，则获胜的概率为，
二是前两局乙胜一局，第三局乙获胜，则获胜的概率为，
而这两种情况是互斥的，所以乙最终获胜的概率为.
故选：B.
3．（2024山东日照）中国梦蕴含航天梦，航天梦助力中国梦.2023年10月25日，神舟十七号载人飞船在酒泉卫星发射中心成功点火发射．在太空站内有甲，乙，丙三名航天员依次出仓进行同一试验，每次只派一人，每人最多出仓一次．若前一人试验不成功，返仓后派下一人重复进行该试验；若试验成功，终止试验．已知甲，乙，丙各自出仓试验成功的概率分别为，，，每人出仓试验能否成功相互独立，则该项试验最终成功的概率为（ ）
A．B．C．D．
【答案】D
【解析】设试验任务不成功的的概率是，
所以成功的概率为，
故选：D.
4．（2024上海杨浦）已知，，，则事件与的关系是（ ）
A．与互斥不对立B．与对立
C．与相互独立D．与既互斥又独立
【答案】C
【解析】由可得，
因为，则与不互斥，不对立，
由可得，
因为，所以与相互独立
故选：C
5．（2024四川凉山）一个盒子中装有标号为1，2，3，4的4张号签，从中随机地选取两张号签，事件“取到标号为1和3的号签”，事件“两张号签标号之和为5”，则下列说法正确的是（ ）
A．与互斥B．与独立C．与对立D．
【答案】A
【解析】根据题意，选取两张号签用表示一次实验结果，
则随机试验结果的样本空间，
，.
对A，，所以与互斥，故A选项正确；
对B，，，，所以，与不独立，故B选项错误；
对C，，，所以与不对立，故C选项错误；
对D，，故D选项错误.
故选：A.
6．（2024江西抚州）从甲袋中摸出一个红球的概率是，从乙袋中摸出一个红球的概率是，从两袋各摸出一个球，下列结论错误的是（ ）
A．2个球都是红球的概率为
B．2个球中恰有1个红球的概率为
C．至少有1个红球的概率为
D．2个球不都是红球的概率为
【答案】D
【解析】记从甲袋中摸出一个红球的事件为，从乙袋中摸出一个红球的事件为，且，，相互独立，
对于A选项，2个球都是红球的事件为，则有，故A正确；
对于B选项，2个球中恰有1个红球的事件为，
则，故B正确；
对于C选项，至少有1个红球的事件的对立事件是，
则，
所以至少有1个红球的概率为，故C正确；
对于D选项，2个球不都是红球的事件是事件的对立事件，其概率为，
故D不正确．故选：D.
7．（2024江西·开学考试）现有张完全相同的卡片，分别写有字母、、、、，从中任取一张，看后再放回，再任取一张.甲表示事件“第一次抽取卡片的字母为”，乙表示事件“第二次抽取卡片的字母为”，丙表示事件“两次抽取卡片的字母相邻”，丁表示事件“两次抽取卡片的字母不相邻”，则（ ）
A．乙与丁相互独立B．甲与丙相互独立
C．丙与丁相互独立D．甲与乙相互独立
【答案】D
【解析】设事件甲、乙、丙、丁分别记为、、、，由题意可得，
有放回的抽取卡片两次的基本事件数为，
两次抽取卡片的字母相邻的基本事件为、、、、、、、，共个，
两次抽取卡片的字母不相邻的基本事件为个，则，，
显然丙与丁为对立事件，C错误；
对于A，乙与丁同时发生的基本事件为、、，有个，
则，所以乙与丁不相互独立，A错误；
对于B，甲与丙同时发生的基本事件、，有个，
则，所以甲与丙不相互独立，B错误；
对于D，甲与乙同时发生的基本事件为，只有个，
则，所以甲与乙相互独立，D正确.
故选：D.
8．（2023·广西）已知甲袋中有标号分别为的四个小球，乙袋中有标号分别为的四个小球，这些球除标号外完全相同，第一次从甲袋中取出一个小球，第二次从乙袋中取出一个小球，事件表示“第一次取出的小球标号为3”，事件表示“第二次取出的小球标号为偶数”，事件表示“两次取出的小球标号之和为7”，事件表示“两次取出的小球标号之和为偶数”，则（ ）
A．与相互独立B．与是对立事件
C．与是对立事件D．与相互独立
【答案】D
【解析】由题意可得基本事件总数为，
设
，

由题意可得与可以同时发生，故不是对立事件，
易知与不同时发生，为互斥事件，但不是对立事件，比如还可以有发生，则错误.
，
则，
从而与不相互独立，与相互独立，故A错误，D正确.
故选：D
多选题
9．（2023·河南安阳·期末）在12张卡片上分别写上数字1~12，从中随机抽出一张，记抽出的卡片上的数字为，甲表示事件“为偶数”，乙表示事件“为质数”，丙表示事件“能被3整除”，丁表示事件“”，则（ ）
A．甲与丙为互斥事件B．乙与丁相互独立
C．丙与丁相互独立D．甲乙乙丙）
【答案】CD
【解析】由已知，该试验的样本空间为．
甲，乙，丙，丁．
对于A，因为甲丙，故甲与丙不互斥，错误；
对于B，乙丁，所以乙丁，
又（乙），（丁），所以（乙）（丁）（乙丁），故乙与丁不相互独立，错误；
对于C，丙丁，所以（丙丁），
又P（丙），P（丁），P（丙）P（丁）=P（丙丁），故丙与丁相互独立，正确；
对于D，甲乙，乙丙，故P（甲乙）=P（乙丙），正确．
故选：CD.
10．（2023高一下·湖南常德·期末）下列四个命题中错误的是（ ）
A．若事件A，B相互独立，则满足
B．若事件A，B，C两两独立，则
C．若事件A，B，C彼此互斥，则
D．若事件A，B满足，则A，B是对立事件
【答案】BCD
【解析】若事件A，B相互独立，则满足，A说法正确；
举例说明：投掷两个骰子，记事件A：第一个骰子的点数为奇数，
事件B：第二个骰子点数为奇数，
事件C：两个骰子的点数之和为奇数，
于是有，，
，可以看出事件A，B，C两两独立，但A，B，C不互相独立，所以，B说法错误；
举例说明：投掷一个骰子三次，记事件A：第一次骰子的点数为1，
事件B：第二次骰子点数为2，
事件C：第三次骰子点数为3，
则
事件A，B，C被此互斥，则，C说法错误；
举例说明：记事件A：投掷一个骰子，骰子的点数为奇数，
事件B：投掷一枚硬币，正面朝上，
则，满足，但A，B不是对立事件，
D说法错误.
故选：BCD
11．（2023浙江·期中）先后两次郑一枚质地均匀的骰子，表示事件“两次郑出的点数之和是6”，表示事件“第二次郑出的点数是偶数”，表示事件“两次郑出的点数相同”，表示事件“至少出现一个奇数点”，则（ ）
A．事件，为互斥事件B．事件，为对立事件
C．D．事件，为相互独立事件
【答案】CD
【解析】因为A事件包含两次掷出点数分别为（3，3），所以事件A，可以同时发生，故A错误；
因为事件“第二次郑出的点数是偶数”与事件“至少出现一个奇数点”可以同时发生，如事件（1,2），故B错误；
因为基本事件空间为，，，，，
，共36个基本事件，至少出现一个奇数的事件共有27个，所以，故C正确；
因为根据C选项可知，，，，
所以，故D正确.
故选：CD
12．（2024河南商丘·期中）设A，B为两个随机事件，若，则下列结论中正确的是（ ）
A．若，则B．若，则A，B相互独立
C．若A与B相互独立，则D．若A与B相互独立，则
【答案】BD
【解析】A，若，则，A错误；
B ，因为，则，B正确；
C，因为A与B相互独立，则也相互独立，
则，C错误；
D，若A与B相互独立，则也相互独立，
则，D正确.
故选：BD
填空题
13．（2023山东淄博·期中）我市男子乒乓球队为备战下届市运会，在某训练基地进行封闭时训练，甲、乙两队队员进行对抗赛，每局依次轮流发球，连续赢两个球者获胜．通过分析甲、乙过去对抗赛的数据知，甲发球甲赢的概率为，乙发球甲赢的概率为，不同球的结果互不影响．已知某局甲先发球，该局打四个球，甲赢的概率是
【答案】
【解析】由于连胜两局者赢，甲先发球可分为：
该局：第一个球甲赢、第二个球乙赢、第三个球甲赢、第四个球甲赢，
则概率为；
故答案为：
14．（2024山东济宁·期中）如图所示，由到的电路中有4个元件，分别为，，，．若，，，能正常工作的概率都是，记事件“到的电路是通路”，则 ．

【答案】
【解析】设“正常工作”，“没有正常工作，正常工作，且中至少有一个正常工作”
由于“到的电路是通路”等价于“正常工作”或“没有正常工作，正常工作，且中至少有一个正常工作”，即
，
由于事件互斥，所以根据互斥事件的概率加法公式，
可得.
故答案为：
15．（2024·安徽芜湖 ）设样本空间含有等可能的样本点，且事件，事件，事件，使得，且满足两两不独立，则 .
【答案】
【解析】由题意，，所以，
所以是共同的唯一的样本点，又两两不独立，即，，，
可见不可以为或，所以为或，即.
故答案为：
16．（2023·云南保山·期末）弘扬中学有一支篮球队，甲、乙为该球队队员，已知甲、乙两名队员投篮命中的概率分别为和.现两人各进行一次投篮比赛，假定两人是否投中互不影响，则甲、乙两人至少有一人投中的概率为 .
【答案】
【解析】甲、乙两人投中的概率分别为，据相互独立事件的概率公式，
甲、乙两人都未投中的概率为，
所以甲、乙两人至少有一个投中的概率为1−=．
故答案为：．
解答题
17．（2023高一上·北京石景山·期末）已知甲投篮命中的概率为0.6，乙投篮不中的概率为0.3，乙、丙两人都投篮命中的概率为0.35，假设甲、乙、丙三人投篮命中与否是相互独立的.
(1)求丙投篮命中的概率；
(2)甲、乙、丙各投篮一次，求甲和乙命中，丙不中的概率；
(3)甲、乙、丙各投篮一次，求恰有一人命中的概率.
【答案】(1)
(2)
(3)
【解析】（1）设甲投篮命中为事件，乙投篮命中为事件，丙投篮命中为事件，
由题意可知，，，，
则，,
所以丙投篮命中的概率为；
（2）甲和乙命中，丙不中为事件，
则，
所以甲和乙命中，丙不中的概率为；
（3）甲、乙、丙各投篮一次，求恰有一人命中为事件，
则,
18．（2024河南）某项考试按科目、科目依次进行，只有当科目成绩合格时，才可继续参加科目的考试．已知每个科目只允许有一次补考机会，两个科目成绩均合格方可获得证书．现某人参加这项考试，科目每次考试成绩合格的概率均为，科目每次考试成绩合格的概率均为．假设各次考试成绩合格与否均互不影响．
(1)求他在科目考试第一次合格的概率；
(2)在这项考试过程中，假设他不放弃所有的考试机会，求他可获得证书的概率．
【答案】(1)
(2)
【解析】（1）科目考试合格的概率为，
则他在科目考试第一次合格的概率为.
（2）他考试的次数为2且获得证书的概率为，
他考试的次数为3且获得证书的概率为，
他考试的次数为4且获得证书的概率为，
所以他可获得证书的概率为.
19．（2024湖北）甲、乙两名射击运动员进行射击比赛，每轮比赛甲、乙各射击一次，已知甲中靶的概率为，乙中靶的概率为，每轮比赛中甲、乙两人射击的结果互不影响，求下列事件的概率：
(1)第一轮射击中恰好有一人中靶；
(2)经过两轮射击，两人共中靶3次
【答案】(1)
(2)
【解析】（1）记每轮比赛中，“甲中靶”为事件，“乙中靶”为事件，
则，
记“第一轮射击中恰好有一人中靶”为事件，
则包含事件甲中靶乙不中靶，或甲不中靶乙中靶，
所以，
所以第一轮射击中恰好有一人中靶的概率为
（2）记“经过两轮射击，两人共中靶3次”为事件，
则
，
所以经过两轮射击，两人共中靶3次概率为
20（2023浙江绍兴·期末）某班学生分A，，，四组参加数学知识竞答，规则如下：四组之间进行单循环（每组均与另外三组进行一场比赛）；每场比赛胜者积3分，负者0分；若出现平局，则比赛双方各积1分.现假设四个组战胜或者负于对手的概率均为，出现平局的概率为，每场比赛相互独立.
(1)求A组在参加两场比赛后得分为3分的概率；
(2)一轮单循环结束后，求四组总积分一样的情况种数，并计算四组总积分一样的概率.
【答案】(1)
(2)7种，
【解析】（1）A组在参加两场比赛后得分为3分的概率为
（2）四组总积分一样，可以每次都是平局，
也可以每组学生是一胜一负一平.
如:
A胜B负，A负C胜，AD平
BC平，B胜D负，C负D胜
不难发现，A的三种情况确定后，比赛结果是确定的，
所以只要去看可能出现的情况，
A胜B负，A负C胜，AD平，
A负B胜，A胜C负，AD平
A胜B负，A负D胜，AC平 ，
A负B胜，A胜D负，AC平
A胜C负，A负D胜， AB平 ，
A负C胜，A胜D负，AB平
共6+1=7种
21．（23-24高一上·江西抚州·期末）2023年9月23日，中国农历象征收获的秋分时节，第19届亚洲运动会在浙江杭州隆重开幕．杭州基础设施全面升级、城市面貌焕然一新、民生服务格局大变．为了解杭州老百姓对城市基础设施升级工作满意度，从该地的A，B两地区分别随机调查了40户居民，根据大家对城市基础设施升级工作的满意度评分（单位：分），得到地区的居民满意度评分的频率分布直方图（如图）和地区的居民满意度评分的频数分布表（如表1）．
表2
(1)根据居民满意度评分，将居民的满意度分为三个等级（如表2），估计哪个地区的居民满意度等级为不满意的可能性大，说明理由.
(2)将频率看作概率，从A，B两地区居民中各随机抽查1户居民进行调查，求至少有一户居民评分满意度等级为“非常满意”的概率
【答案】(1)A地区居民的满意度等级为不满意的可能性更大，理由见解析
(2)0.1925
【解析】（1），，
地区的居民满意度等级为不满意的频率为，
由表1可知地区的居民满意度等级为不满意的频率为，
故地区居民的满意度等级为不满意的可能性更大．
（2）记事件表示“从地区随机抽取一户居民满意度评级为非常满意”，
则．
记事件表示“从地区随机抽取一户居民满意度评级为非常满意”，
则．
事件和事件相互独立，则事件和事件相互独立，
，
记事件表示“至少有一户居民评分满意度等级为非常满意”，
则.
22．（2023云南）插花是一种高雅的审美艺术，是表现植物自然美的一种造型艺术，与建筑、盆景等艺术形式相似，是最优美的空间造型艺术之一。为了通过插花艺术激发学生对美的追求，某校举办了以“魅力校园、花香溢校园”为主题的校园插花比赛。比赛按照百分制的评分标准进行评分，评委由10名专业教师、10名非专业教师以及20名学生会代表组成，各参赛小组的最后得分为评委所打分数的平均分.比赛结束后，得到甲组插花作品所得分数的频率分布直方图和乙组插花作品所得分数的频数分布表，如下所示：

定义评委对插花作品的“观赏值”如下所示：
(1)估计甲组插花作品所得分数的中位数（结果保留两位小数）；
(2)若该校拟从甲、乙两组插花作品中选出1个用于展览，从这两组插花作品的最后得分来看该校会选哪一组，请说明理由（同一组中的数据用该组区间的中点值作代表）；
(3)从40名评委中随机抽取1人进行调查，试估计其对乙组插花作品的“观赏值”比对甲组插花作品的“观赏值”高的概率.
【答案】(1)85.82
(2)选择甲组，理由见解析
(3)0.225
【解析】（1）设甲组插花作品所得分数的中位数为，
由频率分布直方图可得甲组得分在前三个分数区间的频率之和为0.3，在最后三个分数区间的频率之和为0.26，故，
所以，解得.
即估计甲组插花作品所得分数的中位数为85.82
（2）由频率分布直方图可知，甲组插花作品的最后得分约为
由乙组插花作品所得分数的频数分布表，得下表
所以乙组插花作品的最后得分约为
.
因为，所以该校会选择甲组插花作品用于展览
（3）设“对乙组插花作品的‘观赏值’比对甲组插花作品的‘观赏值’高”为事件，
“对乙组插花作品的‘观赏值’为2”为事件，
“对乙组插花作品的‘观赏值’为3”为事件，
“对甲组插花作品的‘观赏值’为1”为事件，
“对甲组插花作品的‘观赏值’为2”为事件，
则.
，，
由频数分布表得，，.
因为事件与相互独立，其中，，所以
，
所以估计该评委对乙组插花作品的“观赏值”比对甲组插花作品的“观赏值”高的概率为0.225
A，B互斥
A，B独立
A，B都发生
A，B都不发生
A，B恰有一个发生
A，B至少有一个发生
A，B至多有一个发生
【解析】
,互斥
,独立
,都发生
,都不发生
,恰有一个发生
,至少有一个发生
,至多有一个发生
满意度评分
频数
2
8
14
10
6
满意度评分
低于70分
满意度等级
不满意
满意
非常满意
分数区间
频数
1
5
12
14
4

3
1
分数区间
观赏值
1
2
3
分数区间
频数
频率
1
0.025
5
0.125
12
0.300
14
0.350
4
0.100

3
0.075
1
0.025