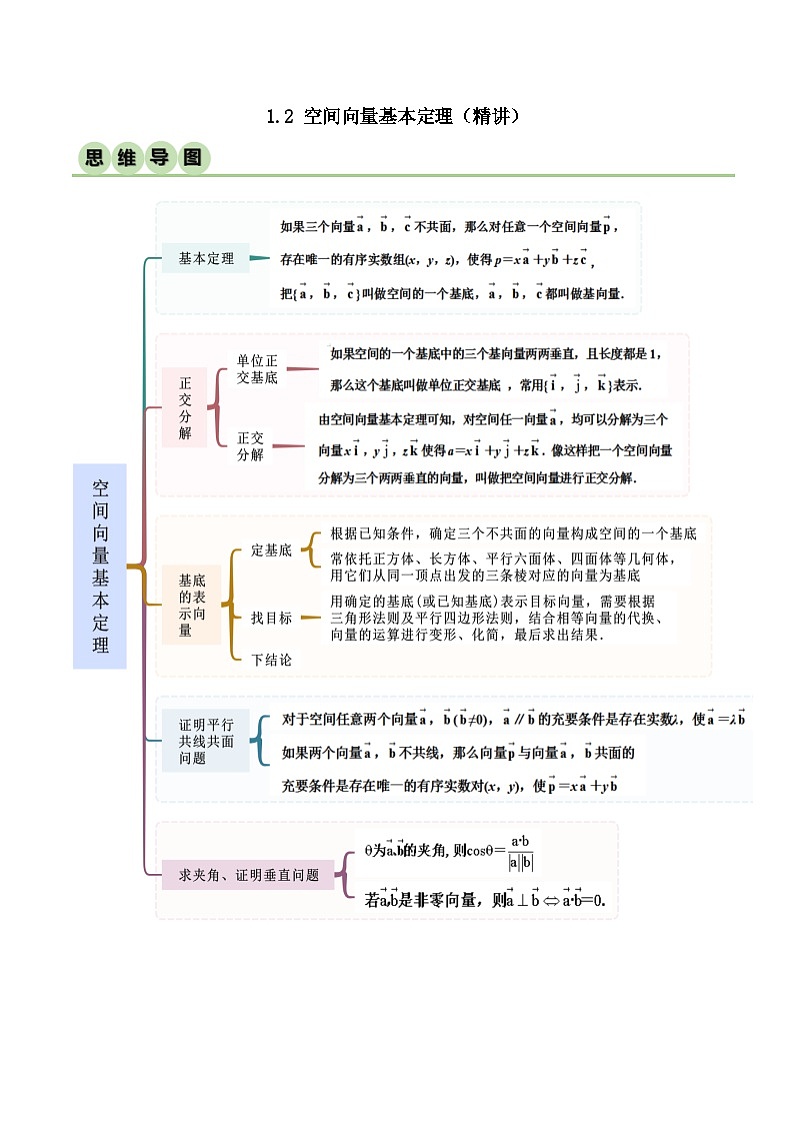

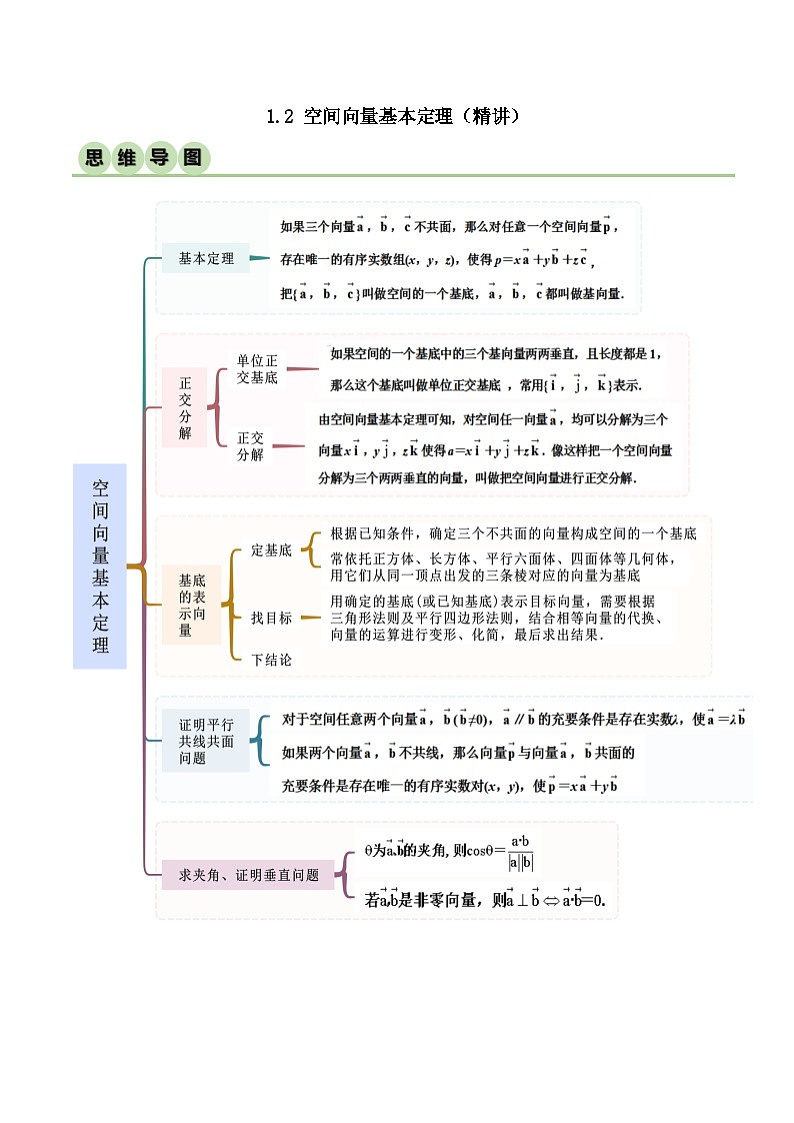


人教A版 (2019)选择性必修 第一册1.2 空间向量基本定理精品随堂练习题
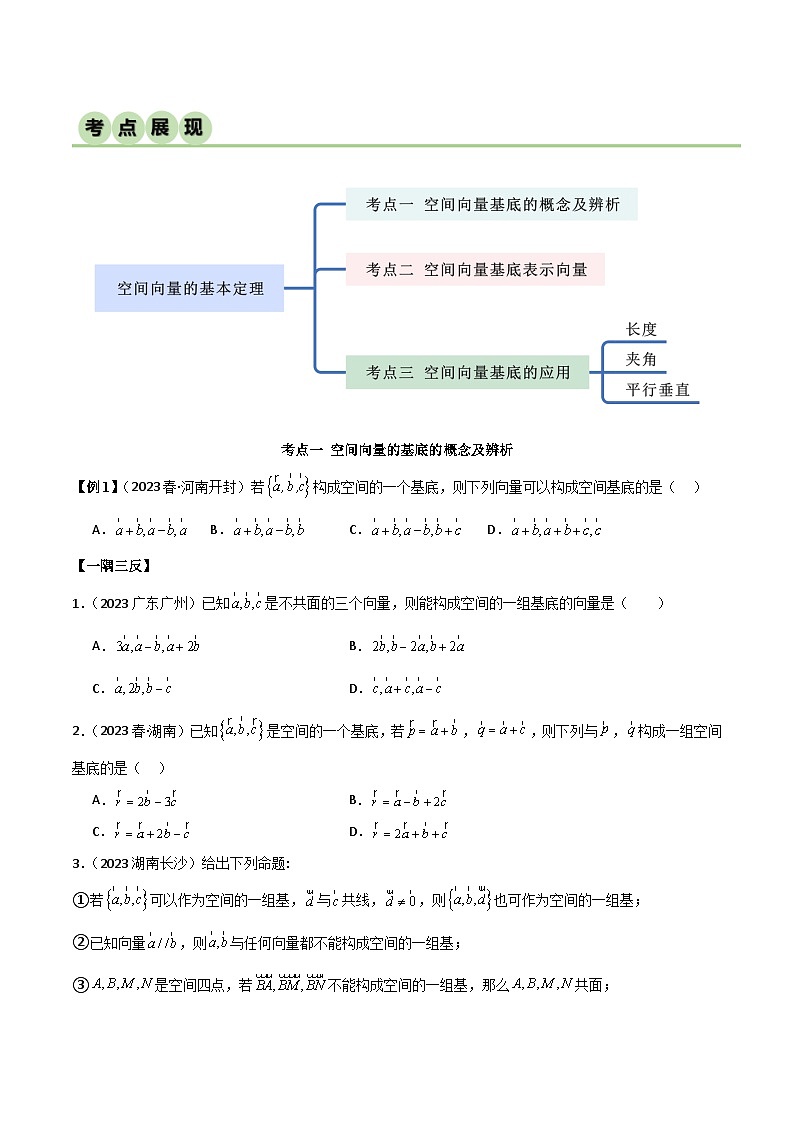
展开考点一 空间向量的基底的概念及辨析
【例1】(2023春·河南开封)若构成空间的一个基底,则下列向量可以构成空间基底的是( )
A.B.C.D.
【答案】C
【解析】对于A,,因此向量共面,故不能构成基底,故A错误;
对于B,,因此向量共面,故不能构成基底,故B错误;
对于C,假设向量共面,则,
即,这与题设矛盾,假设不成立,可以构成基底,故C正确;
对于D,,因此向量共面,故不能构成基底,故D错误;
故选:C.
【一隅三反】
1.(2023广东广州)已知是不共面的三个向量,则能构成空间的一组基底的向量是( )
A.B.
C.D.
【答案】C
【解析】向量是不共面的三个向量,
对于A,,则向量共面,A不是;
对于B,,则向量共面,B不是;
对于D,,则向量共面,D不是;
对于C,假定向量共面,则存在不全为0的实数,使得,
整理得,而向量不共面,则有,显然不成立,
所以向量不共面,能构成空间的一个基底,C是.
故选:C
2.(2023春·湖南)已知是空间的一个基底,若,,则下列与,构成一组空间基底的是( )
A.B.
C.D.
【答案】A
【解析】A.设,所以,
整理得,,
因为是空间的一个基底,所以,无解.
所以,与构成一个基底.
B.因为,所以,所以排除B;
C.因为,所以,所以排除C;
D.设,所以,
整理得,,
因为是空间的一个基底,所以,所以,
所以,与不构成一个基底,排除D.
故选:A
3.(2023湖南长沙)给出下列命题:
①若可以作为空间的一组基,与共线,,则也可作为空间的一组基;
②已知向量,则与任何向量都不能构成空间的一组基;
③是空间四点,若不能构成空间的一组基,那么共面;
④已知是空间的一组基,若,则也是空间的一组基.
其中真命题的个数是( ).
A.1B.2
C.3D.4
【答案】D
【解析】根据空间中任意三个不共面的向量都可构成空间的一组基,显然②正确.
③中由共面且过相同点,故共面.
下面证明①④正确.
①假设与共面,则存在实数,使,
∵与共线,,∴存在实数,使,
∵,∴,从而,∴与共面,与条件矛盾.
∴与不共面.同理可证④也是正确的.故选:D.
考点二 空间向量基底表示向量
【例2-1】(2023·北京)在四面体中,,Q是BC的中点,且M为PQ的中点,若,,,则( )
A.B.
C.D.
【答案】A
【解析】因为,所以,
因为Q是的中点,所以,
因为M为PQ的中点,所以,
故选:A.
【例2-2】(2023春·江苏常州)已知矩形,为平面外一点,平面,点满足,.若,则( )
A.B.C.D.-1
【答案】A
【解析】矩形中,,所以.
因为,所以.
因为,,所以.
所以.
所以,所以.故选:A
【一隅三反】
2.(2023春·江苏常州)如图,是四面体的棱的中点,点在线段上,点在线段上,且,,用向量,,表示,则( )
A.B.
C.D.
【答案】A
【解析】
.
故选:A
2.(2023·全国·高二专题练习)如图,在平行六面体中,P是的中点,点Q在上,且,设,,.则( )
A.B.
C.D.
【答案】C
【解析】因为P是的中点,
所以,
又因为点Q在上,且,
所以
,
所以,
故选:C.
3.(2023春·云南·高二校联考阶段练习)如图,在正方体中,分别为的中点,若,则__________.
【答案】
【解析】因为,
所以所以.
故答案为:.
4.(2023·福建福州)在三棱锥P-ABC中,点O为△ABC的重心,点D,E,F分别为侧棱PA,PB,PC的中点,若,,,则=( )
A.B.C.D.
【答案】D
【解析】取中点为,
三个式子相加可得,
又
,
故选:D
考点三 空间向量基底的应用
【例3-1】(2022秋·天津滨海新·高二天津市滨海新区塘沽第一中学校考阶段练习)已知平行六面体的底面是边长为1的菱形,且,.
(1)证明:;
(2)求异面直线与夹角的余弦值.
【答案】(1)证明见详解;(2)
【解析】设,,
由题可知:两两之间的夹角均为,且,
(1)由
所以即证.
(2)由,又
所以,
又
则
又异面直线夹角范围为
所以异面直线夹角的余弦值为.
【例3-2】(2022秋·广东中山·高二校考阶段练习)在空间四边形ABCD中,H,G分别是AD,CD的中点,E,F分别边AB,BC上的点,且,,,
(1)求(用向量表示);
(2)求证:点E,F,G,H四点共面.
【答案】(1)
(2)证明见解析
【解析】∵
∴
(2)连接
∵分别是的中点,∴.
又∵,∴,
∴,则四点共面.
【一隅三反】
1.(2023·江苏·高二专题练习)已知空间四边形OABC中,,且OA=OB=OC,M,N分别是OA,BC的中点,G是MN的中点,求证:OG⊥BC.
【答案】证明见解析
【解析】在空间四边形OABC中,令,则,
令,G是MN的中点,如图,
则,,
于是得
,
因此,,
所以OG⊥BC.
2.(2022秋·山东聊城·高二山东聊城一中校考阶段练习)如图,在棱长为1的正四面体中,,分别是边,的中点,点在上,且,设,,.
(1)试用向量,,表示向量;
(2)求.
【答案】(1)
(2)
【解析】(1)
(2)由题意知,,,,
则,
,
所以
3.(2023广西)如图,空间四边形的各边及对角线长都为2,E是的中点,F在上,且.
(1)用表示;
(2)求向量与向量所成角的余弦值.
【答案】(1);(2).
【解析】(1)因为E是的中点,F在上,且,
所以,
于是.
(2)由(1)得,
因此,
,
又因为,
所以向量与向量所成角的余弦值为.
人教A版 (2019)必修 第一册1.2 集合间的基本关系练习: 这是一份人教A版 (2019)必修 第一册<a href="/sx/tb_c4000256_t7/?tag_id=28" target="_blank">1.2 集合间的基本关系练习</a>,文件包含人教版高中数学必修一精讲精练12集合间的关系精讲原卷版docx、人教版高中数学必修一精讲精练12集合间的关系精讲解析版docx等2份试卷配套教学资源,其中试卷共21页, 欢迎下载使用。
人教A版 (2019)必修 第一册第一章 集合与常用逻辑用语1.2 集合间的基本关系当堂达标检测题: 这是一份人教A版 (2019)必修 第一册<a href="/sx/tb_c4000256_t7/?tag_id=28" target="_blank">第一章 集合与常用逻辑用语1.2 集合间的基本关系当堂达标检测题</a>,文件包含人教版高中数学必修一精讲精练12集合间的关系精练原卷版docx、人教版高中数学必修一精讲精练12集合间的关系精练解析版docx等2份试卷配套教学资源,其中试卷共24页, 欢迎下载使用。
高中数学人教A版 (2019)选择性必修 第一册1.4 空间向量的应用练习: 这是一份高中数学人教A版 (2019)选择性必修 第一册<a href="/sx/tb_c4000323_t7/?tag_id=28" target="_blank">1.4 空间向量的应用练习</a>,文件包含人教版高中数学选择性必修一精讲精练14空间向量应用精讲原卷版docx、人教版高中数学选择性必修一精讲精练14空间向量应用精讲解析版docx等2份试卷配套教学资源,其中试卷共56页, 欢迎下载使用。













