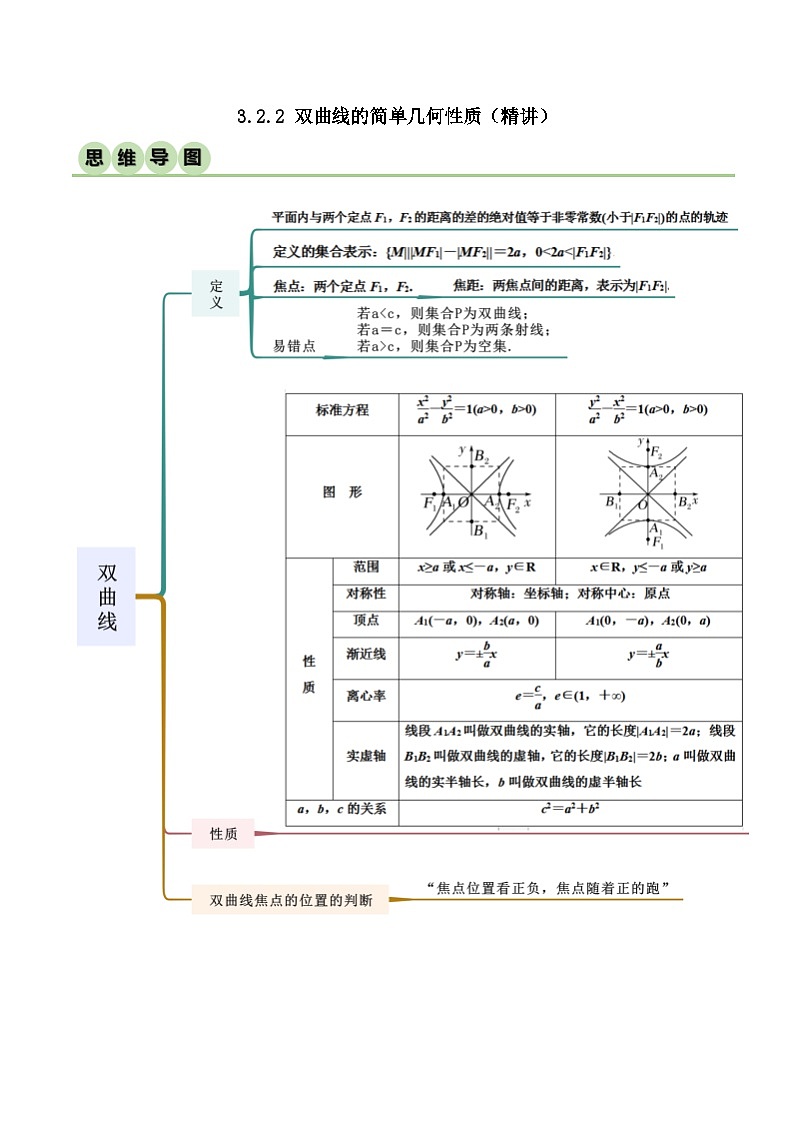
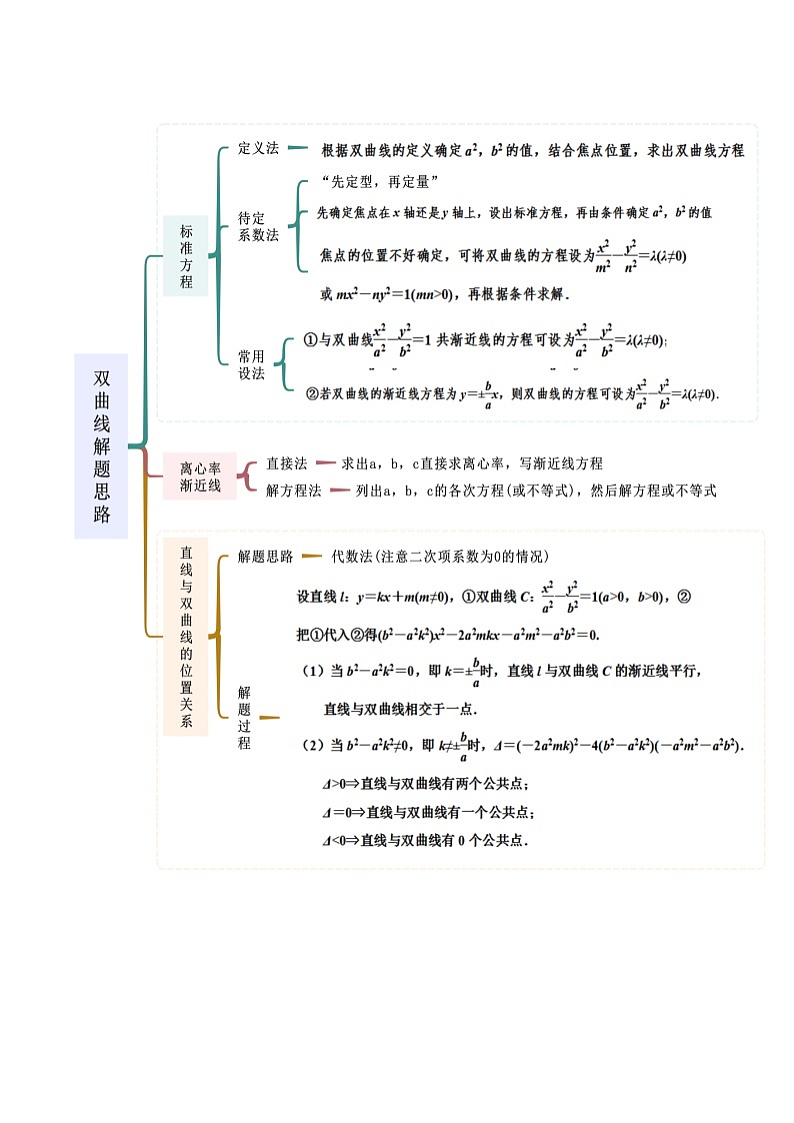
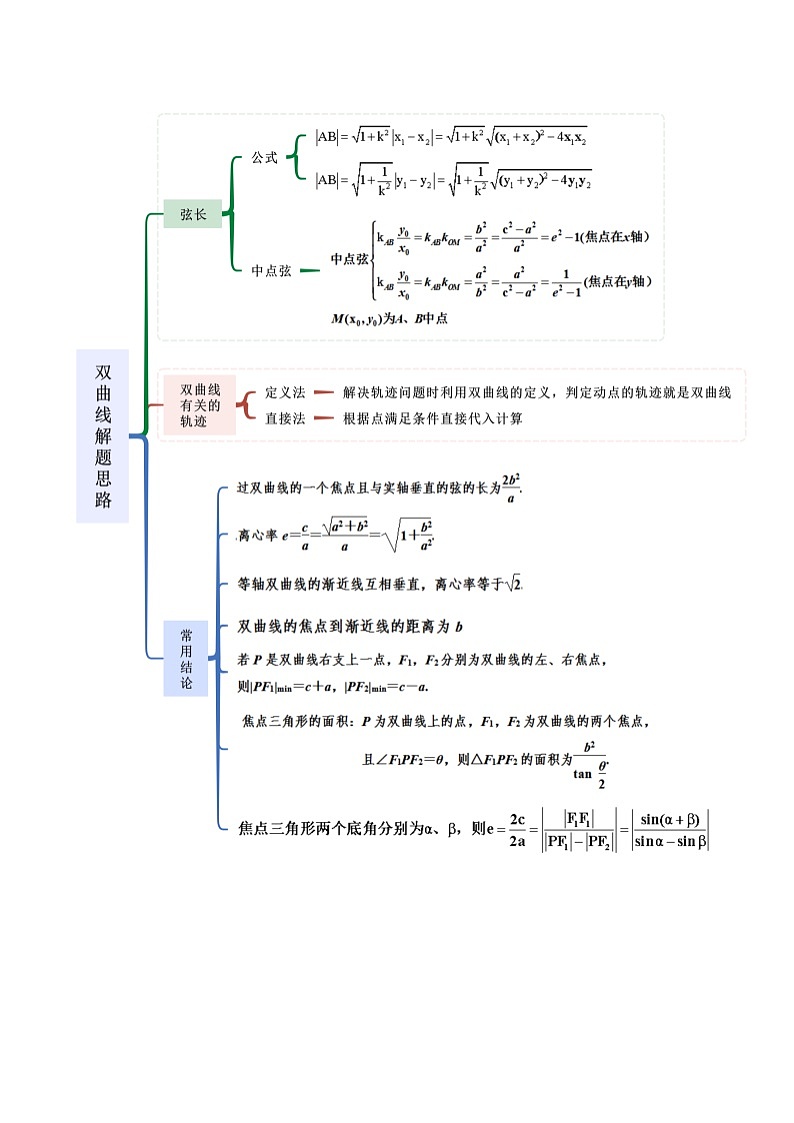
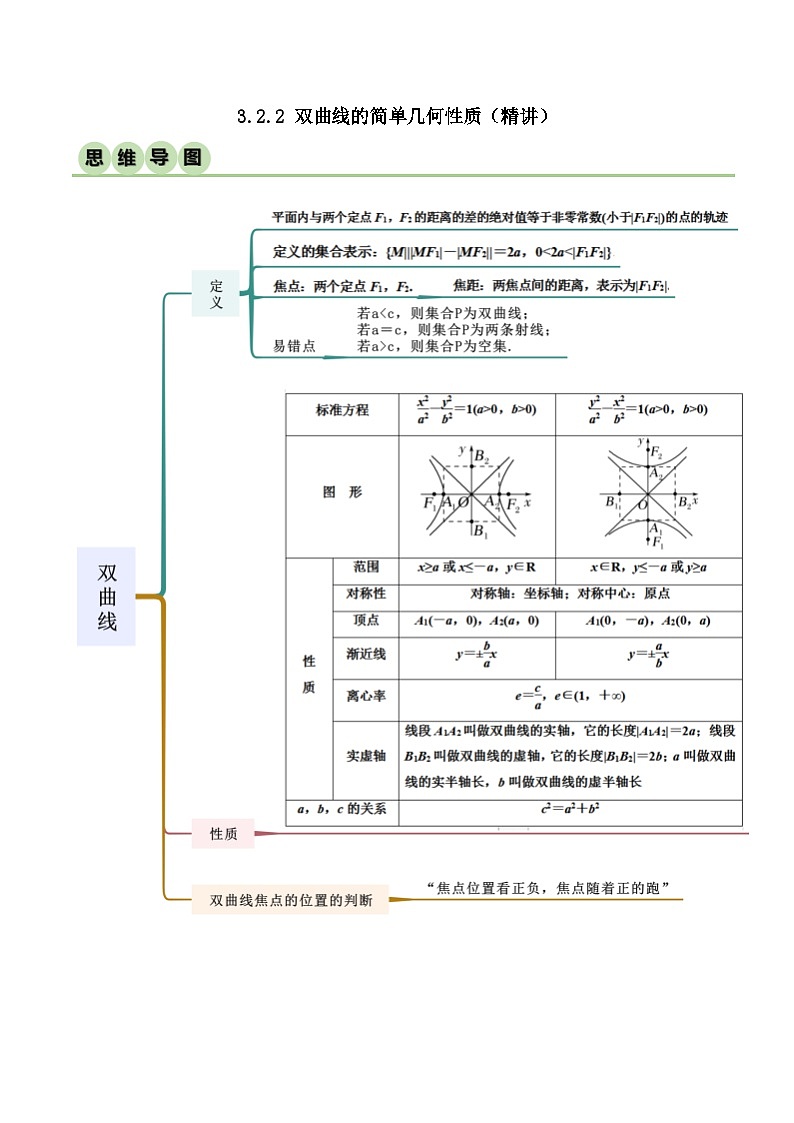
所属成套资源:人教版高中数学选择性必修一 精讲精练 (2份,原卷版+解析版)
人教A版 (2019)选择性必修 第一册3.2 双曲线精品巩固练习
展开
这是一份人教A版 (2019)选择性必修 第一册3.2 双曲线精品巩固练习,文件包含人教版高中数学选择性必修一精讲精练322双曲线的简单几何性质精讲原卷版docx、人教版高中数学选择性必修一精讲精练322双曲线的简单几何性质精讲解析版docx等2份试卷配套教学资源,其中试卷共37页, 欢迎下载使用。
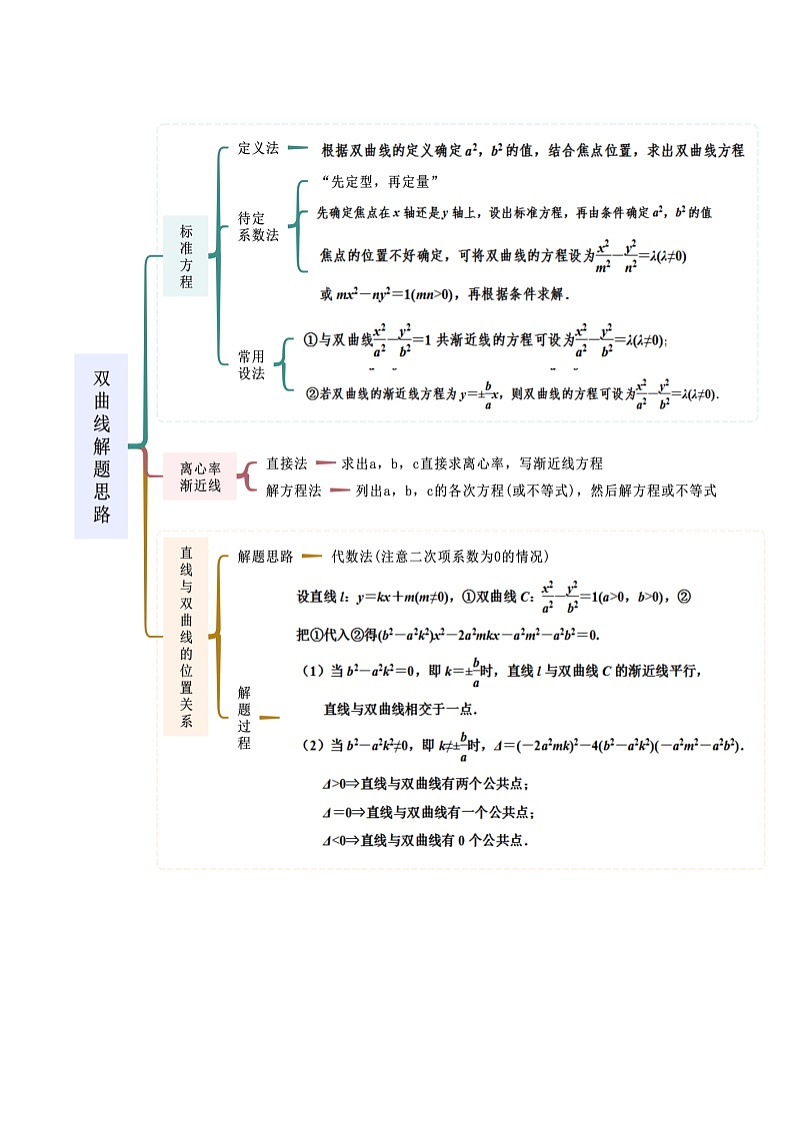
考点一 离心率与渐近线
【例1-1】(2023春·四川资阳·高二统考期末)双曲线的离心率为( )
A.B.C.D.
【例1-2】(2022·高二课时练习)双曲线的渐近线方程为( )
A.B.C.D.
【例1-3】(2023春·山东菏泽·高二统考期末)设双曲线的渐近线方程为,则此双曲线的离心率为( )
A.B.C.D.
【例1-4】(2023春·福建福州·高二福建省福州第八中学校考期末)设为双曲线C:的左、右焦点,过左焦点的直线与在第一象限相交于一点P,若,且直线倾斜角的余弦值为,则的离心率为 .
【一隅三反】
1.(2023·北京大兴·校考三模)实轴长和虚轴长相等的双曲线称为等轴双曲线,则等轴双曲线的离心率为( )
A.B.2C.D.3
2.(2023·四川成都·校考一模)已知中心在原点,焦点在y轴上的双曲线的离心率为,则它的渐近线方程为( )
A.B.
C.D.
3.(2023春·广东·高二统考阶段练习)(多选)已知点是双曲线上任意一点,,是的左、右焦点,则下列结论正确的是( )
A.B.的离心率为
C.D.的渐近线方程为
4.(2023秋·高二课时练习)如果双曲线右支上总存在到双曲线的中心与右焦点距离相等的两个相异点,则双曲线离心率的取值范围是 .
5.(2023秋·河南许昌·高二禹州市高级中学校考期末)过双曲线右焦点作一条渐近线的垂线,分别交两条渐近线于两点,为坐标原点,,的平分线交轴于点,且到渐近线的距离为,则双曲线的离心率为 .
6.(2023·贵州毕节·校考模拟预测)如图,双曲线的左、右焦点分别为,,直线过点与双曲线的两条渐近线分别交于两点.若是的中点,且,则此双曲线的离心率为( )
A.B.2C.D.
考点二 直线与双曲线的位置关系
【例2-1】(2023广东潮州)讨论直线与双曲线的公共点的个数.
【例2-2】(2023·湖北武汉)直线与双曲线的左支交于不同两点,则实数的取值范围为 .
【例2-3】(2022·全国·高三专题练习)求经过点的双曲线:的切线的方程.
【一隅三反】
1.(2023春·上海徐汇·高二上海市徐汇中学校考期中)已知直线和双曲线,若l与C的右支交于不同的两点,则t的取值范围是 .
2.(2022·全国·高三专题练习)设双曲线:上点.求双曲线在点处的切线的方程.
3.(2023秋·高二课时练习)已知双曲线,讨论直线与这条双曲线的交点的个数.
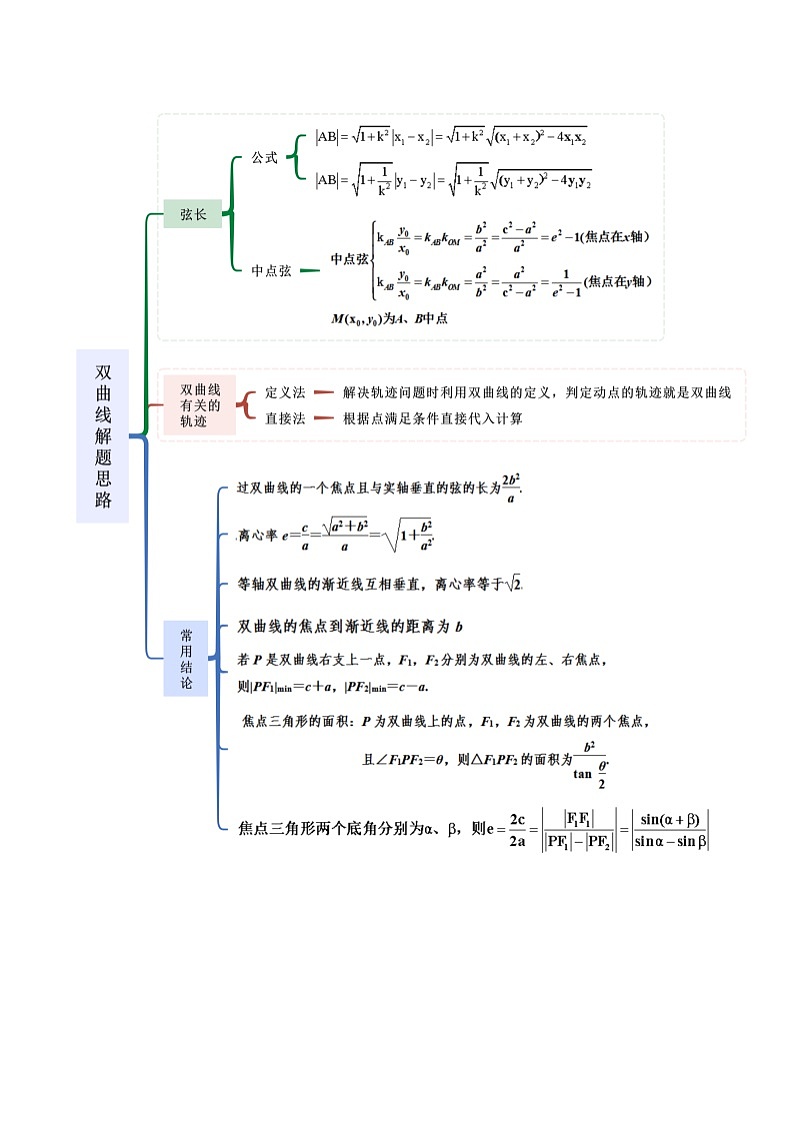
考点三 弦长及其应用
【例3-1】(2023·江苏南京)如图,已知圆,Q是圆上一动点,AQ的垂直平分线交直线CQ于点M,设点M的轨迹为E.
(1)求轨迹E的方程:
(2)过点A作倾斜角为的直线l交轨迹E于B,D两点,求|BD|的值.
【例3-2】(2023秋·高二课时练习)已知双曲线的中心在原点,焦点在坐标轴上,离心率为,且过点,点在双曲线上.求:
(1)双曲线的方程;
(2);
(3)的面积.
【一隅三反】
1.(2023春·新疆阿勒泰·高二统考期末)已知双曲线的实轴长为2,右焦点为.
(1)求双曲线的方程;
(2)已知直线与双曲线交于不同的两点,,求.
2.(2023春·四川资阳·高二统考期末)已知双曲线实轴长为2,左、右两顶点分别为,,上的一点分别与,连线的斜率之积为3.
(1)求的方程;
(2)经过点的直线分别与的左、右支交于M,N两点,为坐标原点,的面积为,求的方程.
3.(2023春·上海宝山·高二上海交大附中校考期中)已知双曲线,及直线.
(1)若与有且只有一个公共点,求实数的值;
(2)若与的左右两支分别交于A、B两点,且的面积为,求实数的值.
考点四 中点弦及其应用
【例4-1】(2023春·陕西榆林·高二统考期末)已知为双曲线上两点,且线段的中点坐标为,则直线的斜率为( )
A.B.C.D.
【例4-2】(2023春·湖北孝感·高二校联考期中)过点的直线与双曲线相交于两点,若是线段的中点,则直线的方程是( )
A.B.
C.D.
【例4-3】(2023·贵州·校联考模拟预测)已知直线与双曲线的两条渐近线分别交于点,(不重合),的垂直平分线过点,则双曲线的离心率为( )
A.B.C.D.
【一隅三反】
1.(2022秋·高二课时练习)已知双曲线过点作一直线交双曲线于A、B两点,并使P为AB的中点,则直线AB的斜率为( )
A.3B.4
C.5D.6
2.(2023春·宁夏吴忠·高二吴忠中学校考期末)已知双曲线,过点作直线与双曲线交于两点,且点恰好是线段的中点,则直线的方程是( )
A.B.
C.D.
3.(2023秋·浙江宁波·高二校联考期末)过双曲线内一点且斜率为的直线交双曲线于两点,弦恰好被平分,则双曲线的离心率为( )
A.B.C.D.
考点五 双曲线的实际应用
【例5-1】(2023春·河南商丘·高二虞城县高级中学校联考开学考试)如图所示,某拱桥的截面图可以看作双曲线的图象的一部分,当拱顶M到水面的距离为4米时,水面宽AB为米,则当水面宽度为米时,拱顶M到水面的距离为( )
A.4米B.米C.米D.米
【例5-2】(2023·高二课时练习)人们在进行工业设计时,巧妙地利用了圆锥曲线的光学性质.如图,从双曲线右焦点发出的光线通过双曲线镜面反射出发散光线,且反射光线的反向延长线经过左焦点.已知双曲线的方程为,则当入射光线和反射光线互相垂直时(其中为入射点),的大小为( )
A.B.C.D.
【一隅三反】
1(2022秋·高二课时练习)某中心接到其正东、正西、正北方向三个观测点的报告;正西、正北两个观测点同时听到了一声巨响,正东观测点听到的时间比其它两观测点晚2s,已知各观测点到该中心的距离是680m,则该巨响发生在接报中心的( )处(假定当时声音传播的速度为340m/s,相关各点均在同一平面上)
A.西偏北45°方向,距离340mB.东偏南45°方向,距离340m
C.西偏北45°方向,距离170mD.东偏南45°方向,距离170m
2.(2022秋·吉林四平·高三四平市第一高级中学校考阶段练习)人利用双耳可以判定声源在什么方位,听觉的这种特性叫做双耳定位效应(简称双耳效应).根据双耳的时差,可以确定声源必在以双耳为左右焦点的一条双曲线上.又若声源所在的双曲线与它的渐近线趋近,此时声源对于测听者的方向偏角,就近似地由双曲线的渐近线与虚轴所在直线的夹角来确定.一般地,甲测听者的左右两耳相距约为,声源的声波传及甲的左、右两耳的时间差为,声速为,则声源对于甲的方向偏角的正弦值约为( )
A.0.004B.0.04C.0.005D.0.05
3.(2023·全国·高三专题练习)3D打印是快速成型技术的一种,通过逐层打印的方式来构造物体.如图所示的笔筒为3D打印的双曲线型笔筒,该笔筒是由离心率为3的双曲线的一部分围绕其旋转轴逐层旋转打印得到的,已知该笔筒的上底直径为6cm,下底直径为8cm,高为8cm(数据均以外壁即笔筒外侧表面计算),则笔筒最细处的直径为( )
A.B.C.D.
相关试卷
这是一份人教A版 (2019)必修 第一册3.2 函数的基本性质课后作业题,文件包含人教版高中数学必修一精讲精练322函数的奇偶性精讲原卷版docx、人教版高中数学必修一精讲精练322函数的奇偶性精讲解析版docx等2份试卷配套教学资源,其中试卷共36页, 欢迎下载使用。
这是一份高中数学人教A版 (2019)必修 第一册3.2 函数的基本性质测试题,文件包含人教版高中数学必修一精讲精练322函数的奇偶性精练原卷版docx、人教版高中数学必修一精讲精练322函数的奇偶性精练解析版docx等2份试卷配套教学资源,其中试卷共40页, 欢迎下载使用。
这是一份人教A版 (2019)必修 第一册3.2 函数的基本性质巩固练习,文件包含人教版高中数学必修一精讲精练321函数的单调性精讲原卷版docx、人教版高中数学必修一精讲精练321函数的单调性精讲解析版docx等2份试卷配套教学资源,其中试卷共36页, 欢迎下载使用。










